Математическое моделирование и вычислительные технологии в науке и образовании: Межвузовский сборник научных трудов. Выпуск Сургут: рио сургпи, 2005 С
| Вид материала | Документы |
- О. В. Неценко кандидат педагогических наук, 4305.96kb.
- Статья опубликована: Возрождение: Общественно-политическая и историческая мысль, человек, 222.14kb.
- Зубайдуллин А. А., Салихова Н. М., Коротаев, 86.11kb.
- Приложение 1 Международная конференция, 67.26kb.
- Э. В. Паничева (вгпу) кандидат исторических наук, доцент, 1890.45kb.
- Э. В. Паничева (вгпу) кандидат психологических наук, доцент, 2210.7kb.
- Список опубликованных работ доцентом В. М. Шуваловым за период с 2000 по 2004, 43.03kb.
- Вопросы прикладной лингвистики сборник научных трудов москва Издательство Российского, 1099.28kb.
- Ю. В. Сергаева имена групп как объект словотворчества, 123.43kb.
- Сборник научных трудов кафедры, 4077.54kb.
Математическое моделирование и вычислительные технологии в науке и образовании: Межвузовский сборник научных трудов. Выпуск 2.-Сургут:РИО СурГПИ, 2005 – С. 14-22
Ю. А. Сигунов, И. Р. Сабитова
НЕЯВНЫЕ ОДНОШАГОВЫЕ СХЕМЫ С ПРОИЗВОДНЫМИ
ДЛЯ ИНТЕГРИРОВАНИЯ ЖЕСТКИХ СИСТЕМ
И СИСТЕМ МЕТОДА ПРЯМЫХ
Жесткие задачи возникают при численном интегрировании дифференциальных уравнений, описывающих разнообразные модели динамических систем, компоненты решений которых имеют различающиеся на порядки скорости изменения в различные моменты времени [1]. Стандартные методы решения требуют для них чрезвычайно малого шага интегрирования, что приводит к непроизводительным затратам вычислительных ресурсов. Наличие жестких задач привело к разработке большого числа методов, ориентированных на их специфику и характеризующихся повышенными требованиями устойчивости и меньшими ограничениями на шаг интегрирования [2, 3]. Подавляющее большинство таких методов являются неявными.
До настоящего времени проблема построения эффективных схем остается актуальной, так как обеспечение общей их эффективности осложняется проблемой одновременной совместимости таких важных качеств алгоритмов, как порядок точности (в том числе его эффективная величина на жестких задачах), специфические требования на устойчивость, скорость сходимости, простота алгоритмической реализации, общая вычислительная затратность при расчете временного шага. Все эти желаемые качества схем чаще всего находятся в противоречии друг другу. Кроме того, сами жесткие задачи включают различные группы со своими специфическими особенностями, что дополнительно осложняет выбор алгоритма решения.
К жестким задачам относятся и системы дифференциальных уравнений, возникающие при решении уравнений с частными производными методом прямых, когда дискретизация задачи производится только по пространственным переменным. Разделение процедуры пространственной и временной дискретизации при решении задач для уравнений с частными производными дает свои преимущества, в частности получение алгоритмов с более высоким порядком аппроксимации по времени. Системы дифференциальных уравнений, получающиеся в результате пространственной дискретизации, имеют большую размерность и ленточную структуру матрицы системы. Жесткость задач проявляется в ограничениях на величину шага по времени в зависимости от пространственного шага по требованиям устойчивости. Эффективность применения неявных алгоритмов высокого порядка из применяемых для решения жестких систем ставит для таких задач свои критерии.
Большинство предлагаемых в настоящее время алгоритмов решения жестких систем основано на неявных многостадийных методах Рунге-Кутты и их различных подклассах: диагонально-неявных (DIRK), однократно диагонально-неявных (SDIRK), методах Розенброка-Ваннера (ROW), FSAL-схемах [3 – 7].
Среди неявных схем решения обыкновенных дифференциальных уравнений выделяется другой интересный подкласс, характеризующийся включением в расчетный алгоритм наряду со значениями правых частей также и значений их первых производных [8]. Такие схемы являются одношаговыми и одностадийными и обладают неплохими априорными свойствами. При использовании модифицированной итерационной процедуры Ньютона вычислительная затратность и алгоритмическая сложность расчета одного временного шага сопоставима или меньше, чем у аналогичных неявных методов с близкими свойствами. В работе [8] рассмотрены три схемы соответственно второго, третьего и четвертого порядков точности, которые имеют совершенно однотипную реализацию временного шага, несмотря на разный порядок точности. В то же время с ростом порядка точности ухудшаются их качества устойчивости, что считается нежелательным для методов решения жестких задач.
В данной работе представлены сопоставительные результаты апробации вычислительных алгоритмов, основанных на указанном подклассе схем на тестовых жестких системах, а так же их обобщений на дифференциально-разностные системы уравнений, возникающие при решении задач теплопроводности методом прямых.
Для задачи Коши
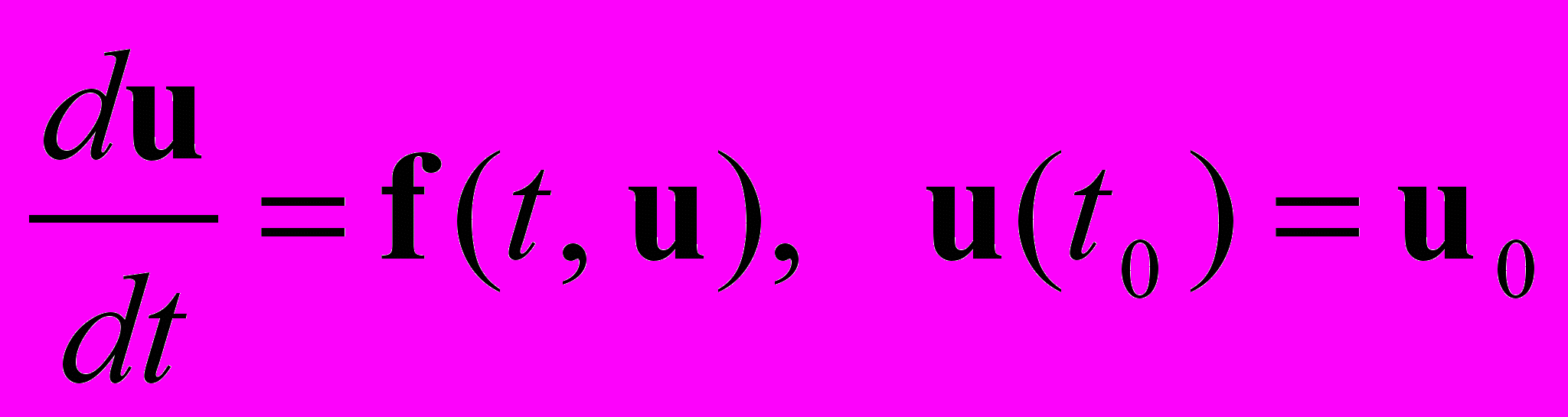 , (1)
, (1)где u = (u1(t), u2(t), …, un(t)) – вектор-функция неизвестных, f = (f1, f2, …, fn) – вектор правой части, fk = fk(t, u1, u2, … , un), u0 = (u10, u20, …, un0) – вектор начальных условий, построение схем основано на интегрировании (1) по интервалу [tm, tm+1]:
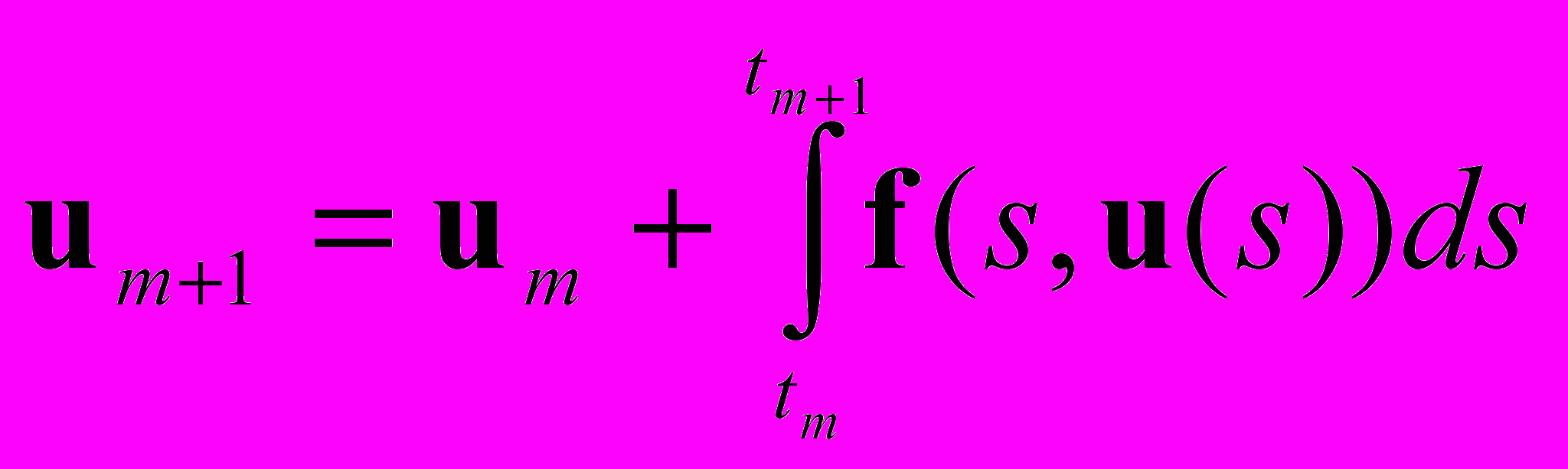 (2)
(2)с последующей заменой неизвестной подынтегральной функции некоторым приближением.
Использование при аппроксимации только узловых значений функции f(t, u(t)) на отрезке интегрирования ограничивает нас двумя стандартными неявными одношаговыми неявными схемами Эйлера и средних соответственно первого и второго порядка точности:
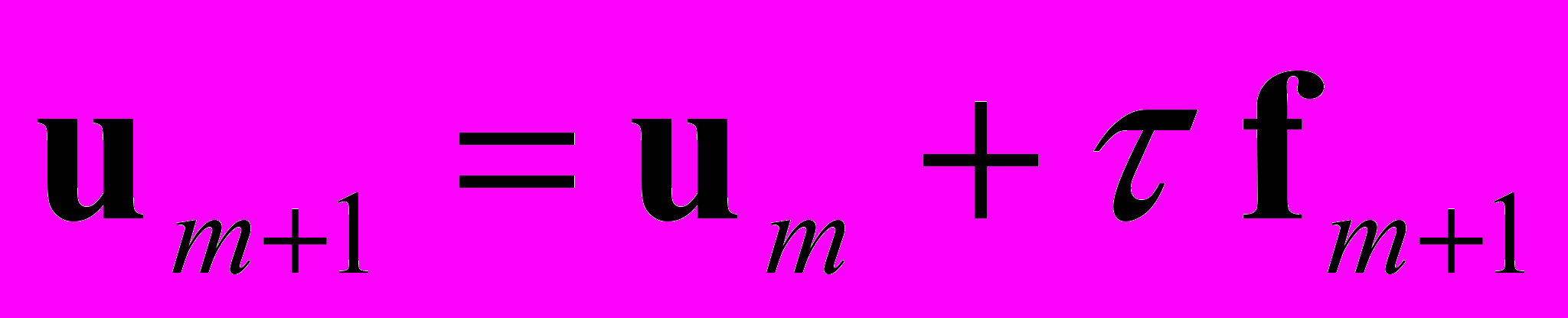 , (3)
, (3)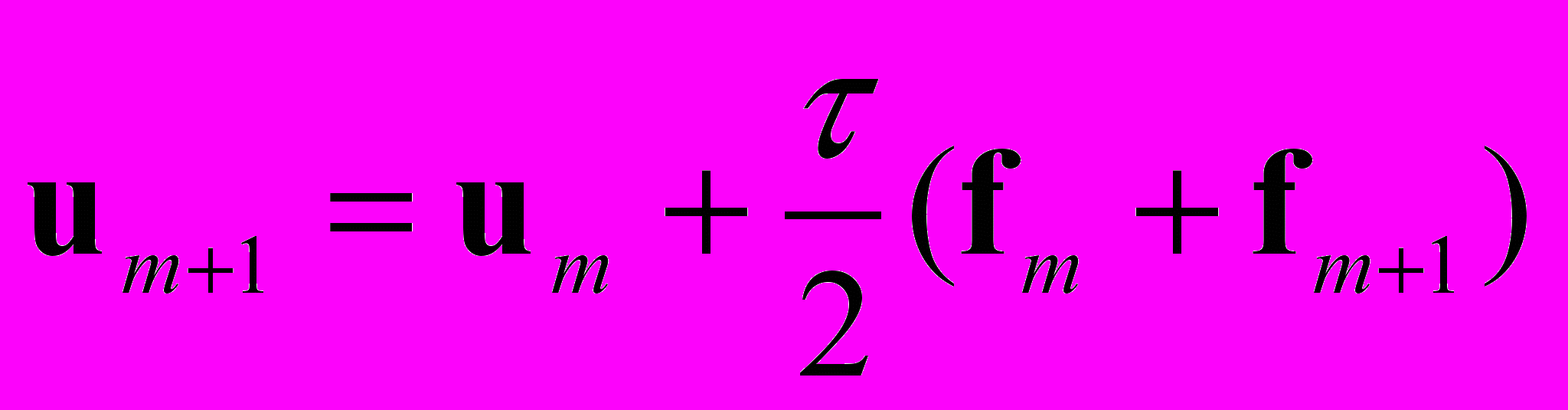 , (4)
, (4)где = tm+1 – tm – шаг по времени, fm = f(tm, um).
Дополнительное привлечение для аппроксимации функции f(t, u(t)) узловых значений ее производной
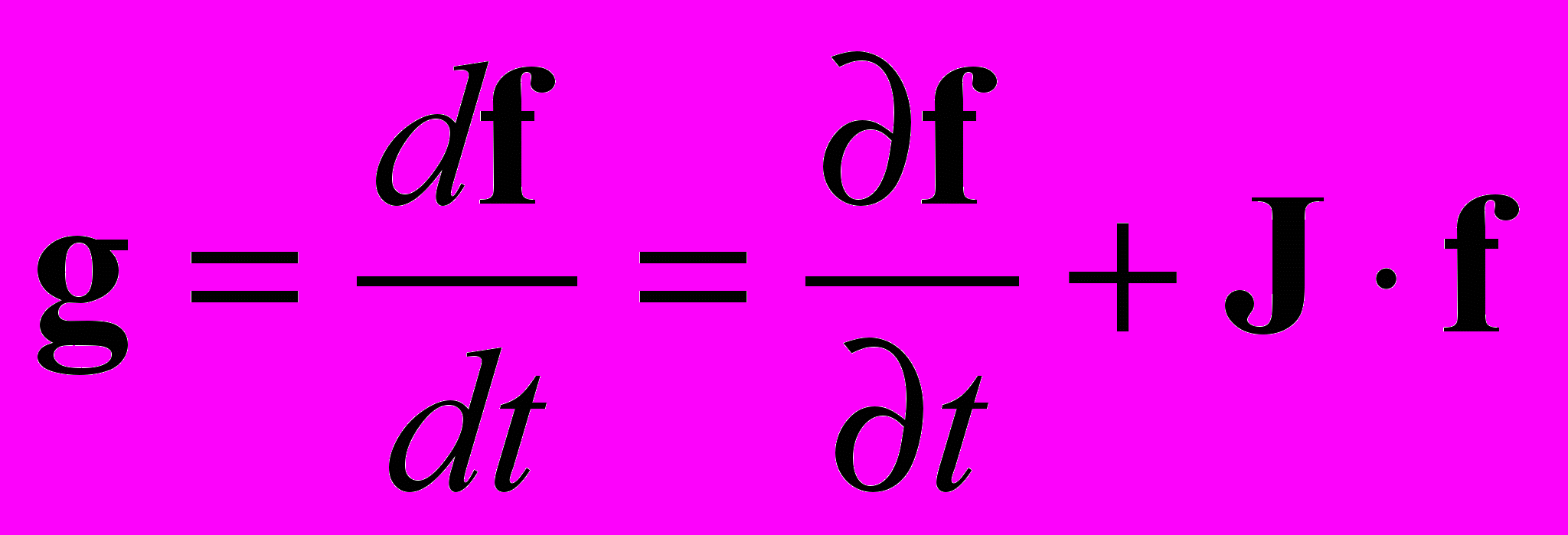 ,
, 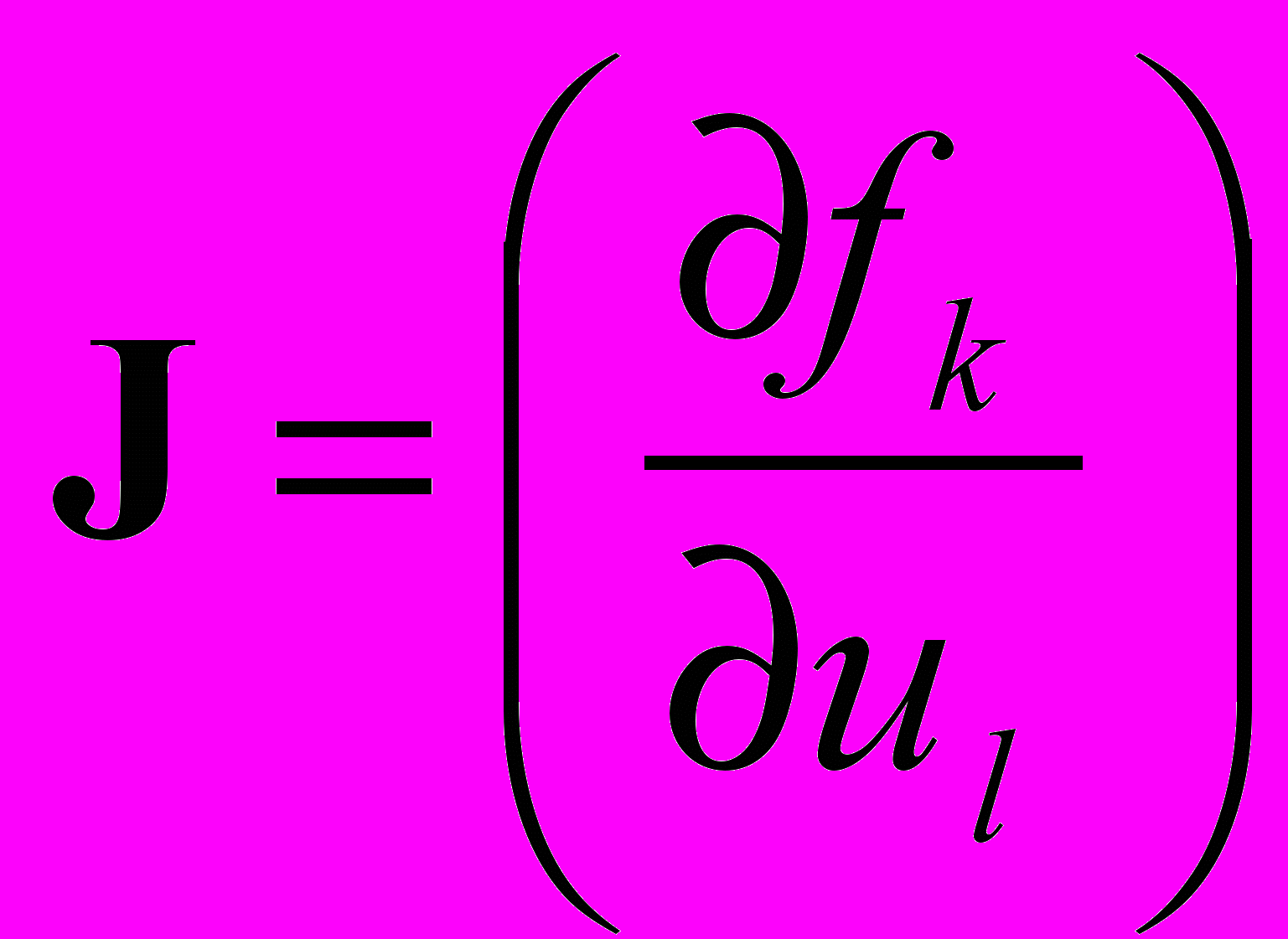 – матрица Якоби вектор-функции f,
– матрица Якоби вектор-функции f,в точках tm и tm+1 дает три одношаговые неявные схемы соответственно второго, третьего и четвертого порядка точности:
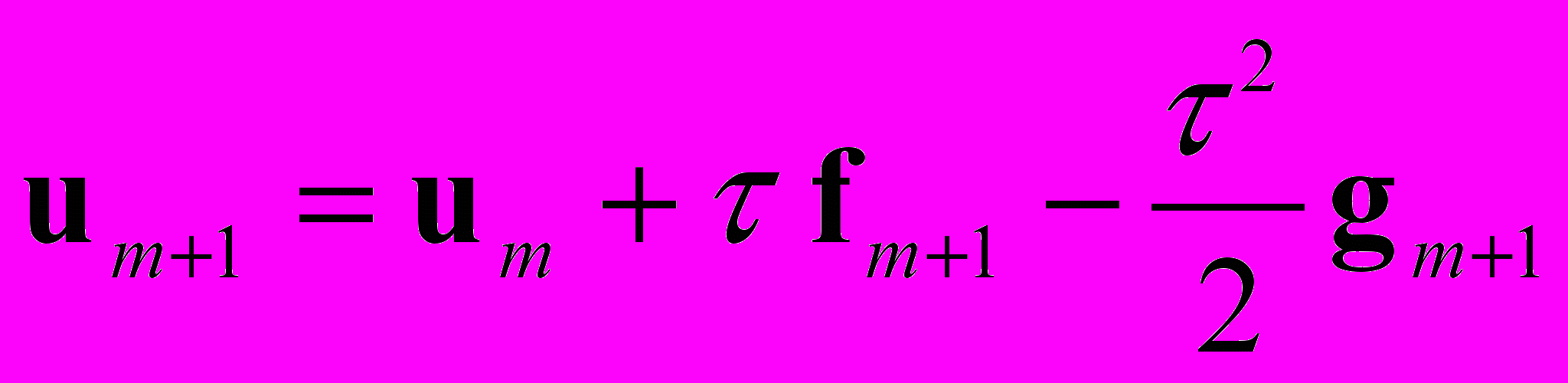 , (5)
, (5)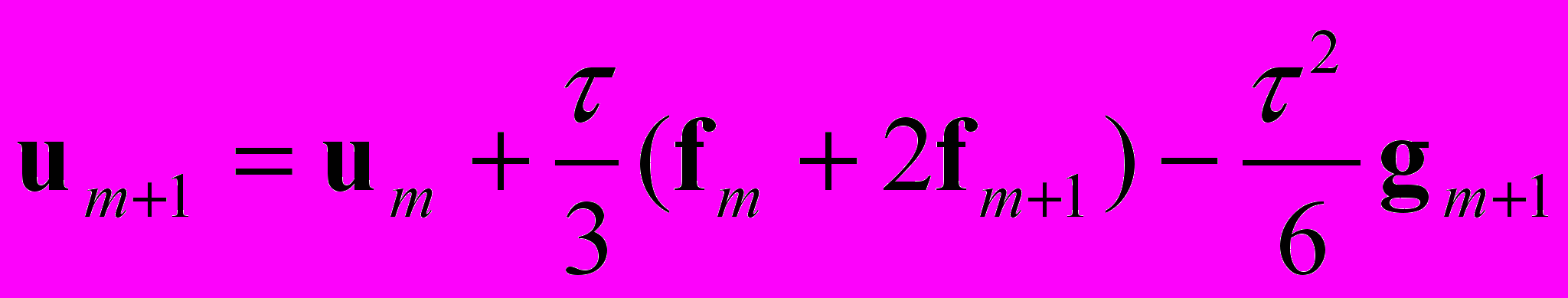 , (6)
, (6)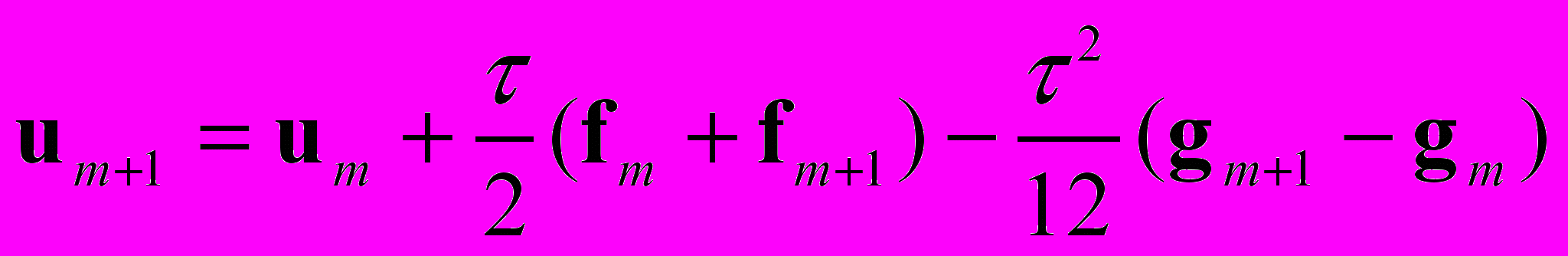 . (7)
. (7)Так как данные схемы содержат в правых частях компоненты матрицы Якоби, для избежания появления тензора вторых производных расчет временного шага осуществляется по упрощенной итерационной процедуре метода Ньютона, пренебрегающей вариацией компонент матрицы Якоби в пределах итерационного цикла, что эквивалентно следующей замене
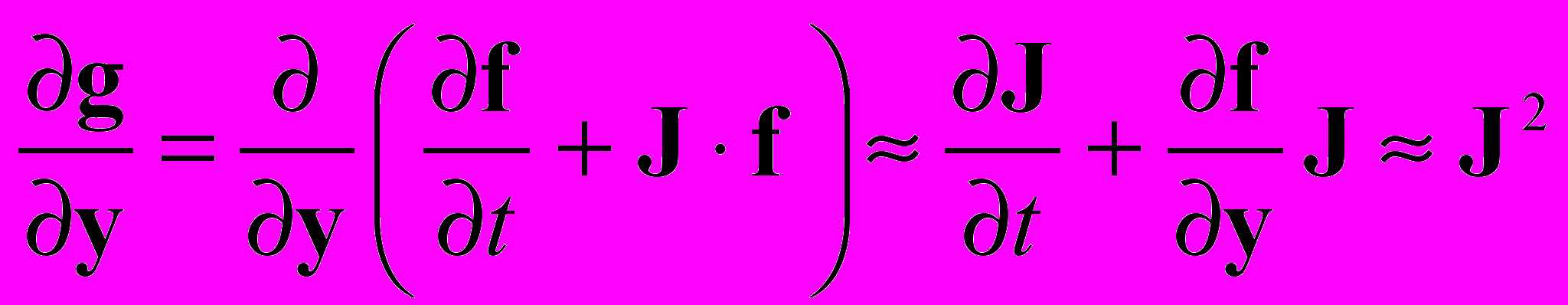 ,
,где y = um+1 – вектор неизвестных компонент решения на новом слое. В результате расчет временного шага для схем (5)–(7) сводится к итерационным процедурам
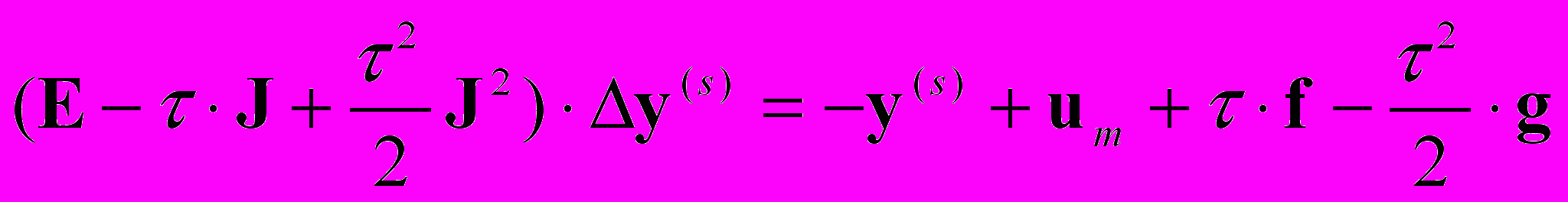 , (8)
, (8)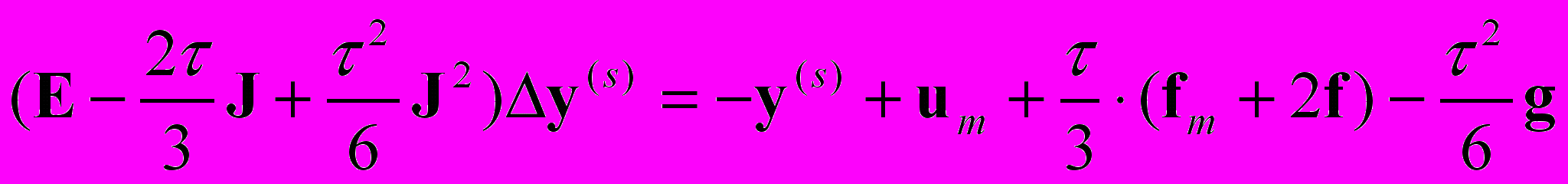 , (9)
, (9)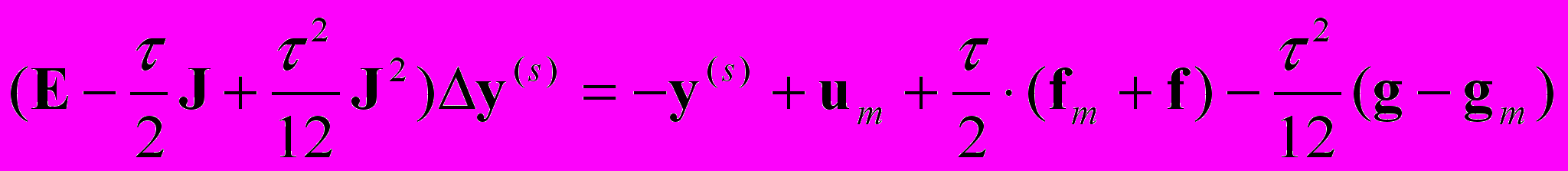 , (10)
, (10)где
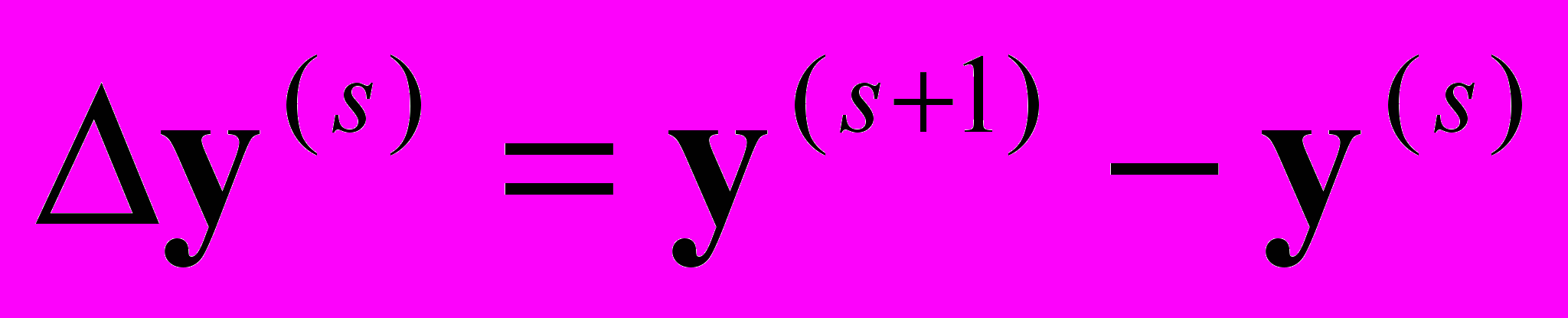 ,
, 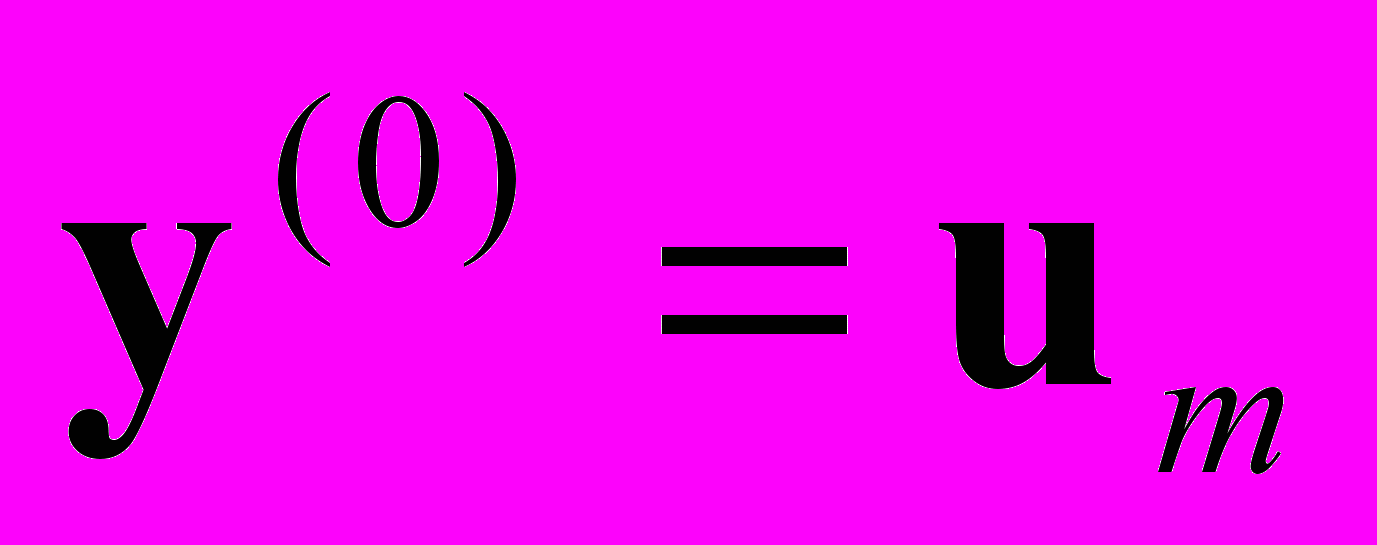 , s – номер итерации.
, s – номер итерации.В отличие от схем Рунге–Кутты алгоритмическая реализация всех трех схем одинакова и не усложняется с увеличением их порядка. В то же время с повышением порядка точности ухудшается качество устойчивости схем. Схема второго порядка является L2-устойчивой, схема третьего порядка L1-устойчивой, а схема четвертого порядка лишь А-устойчивой. Задачей численных экспериментов являлась оценка эффективности данных схем, имеющих разное соотношение в свойствах порядка точности и качества устойчивости.
Применение схем с производными к решению уравнений в частных производных рассмотрим на примере уравнения теплопроводности
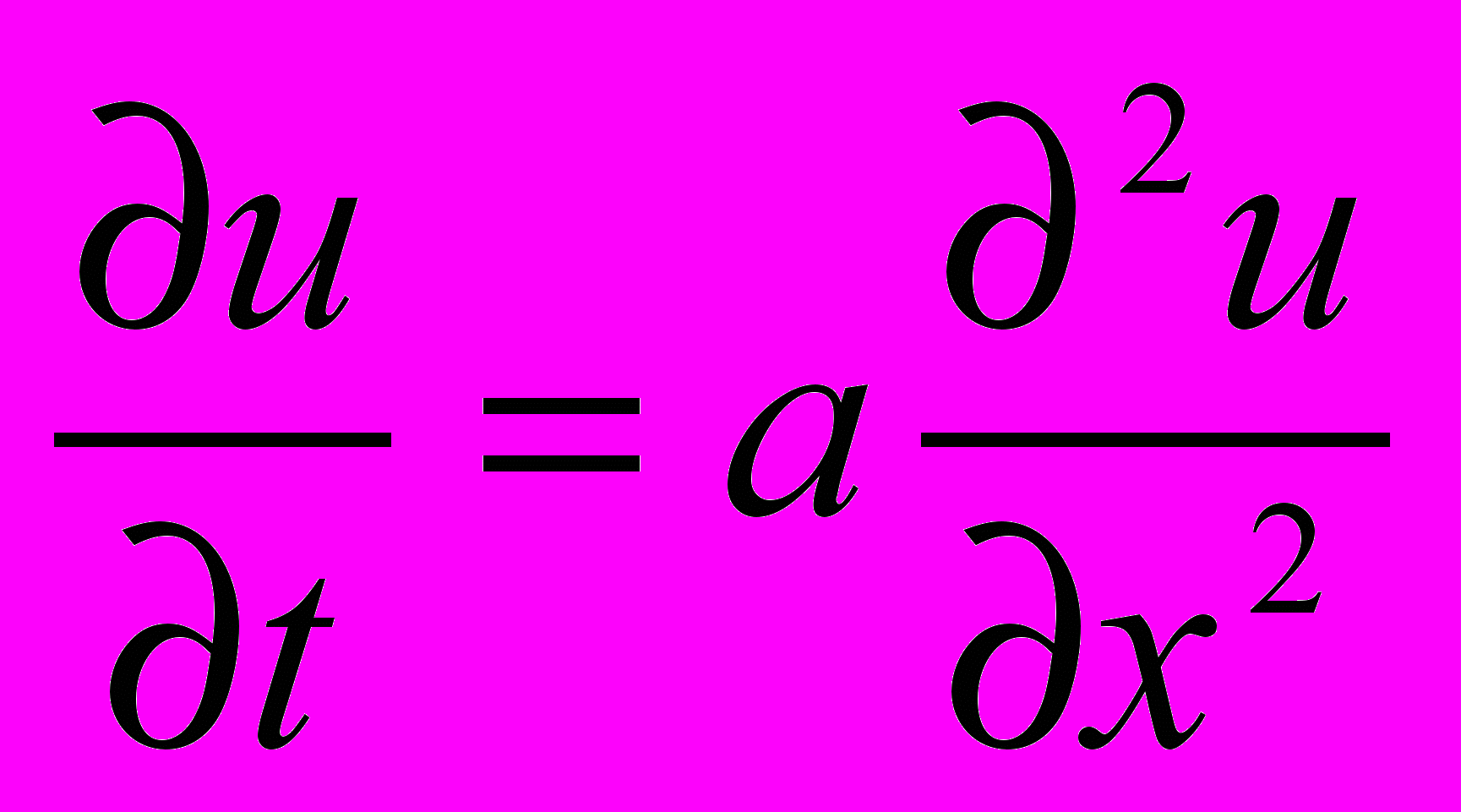 .
.Использование конечно-разностной аппроксимации второй производной на равномерной сетке с шагом h приводит к системе уравнений относительно неизвестных узловых функций
 :
: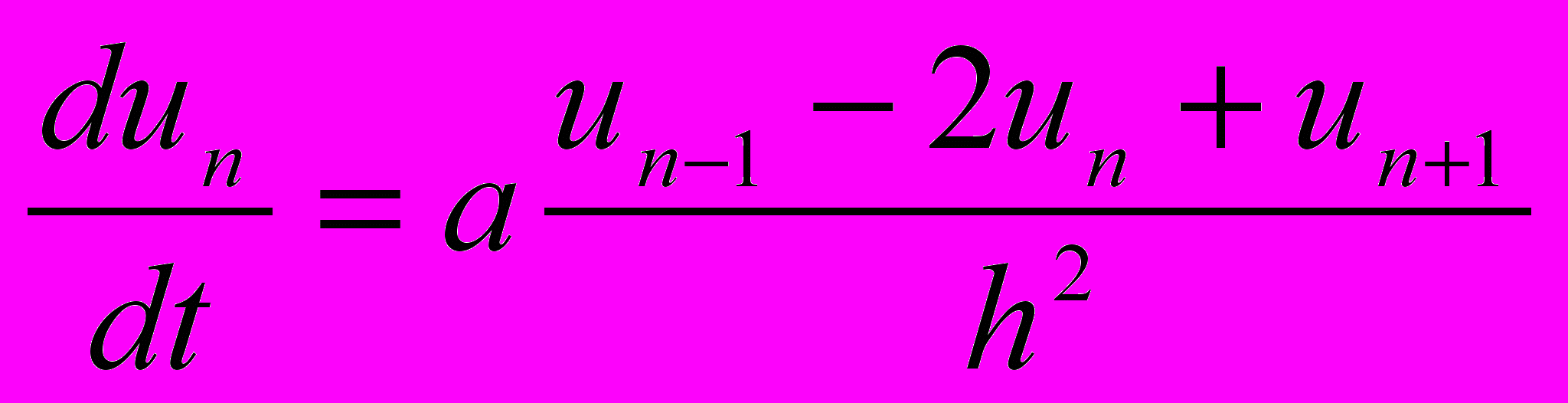 . (11)
. (11)Правая часть системы линейна относительно неизвестных, так что
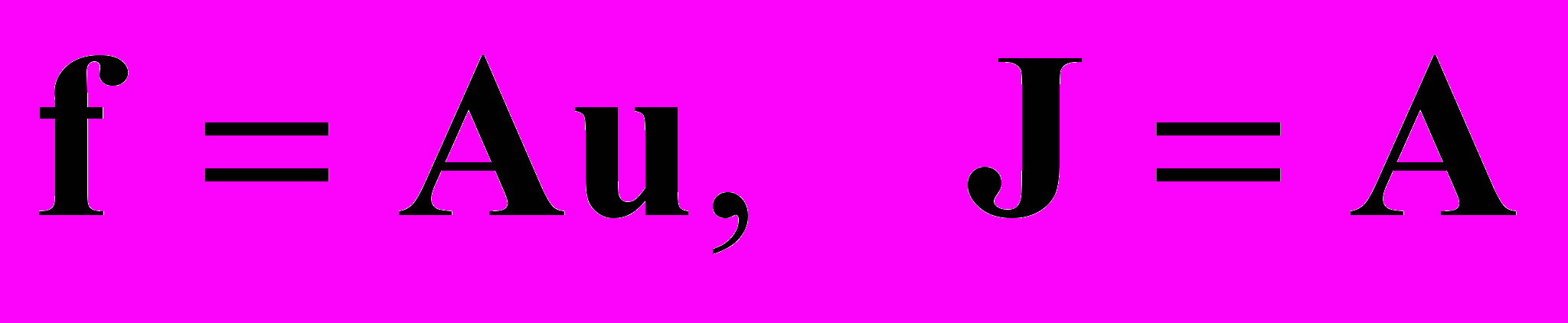 ,
, где А – трехдиагональная числовая матрица.
Интегрирование по времени системы (11) методами Эйлера (3) и средних (4) соответствует известным неявной схеме
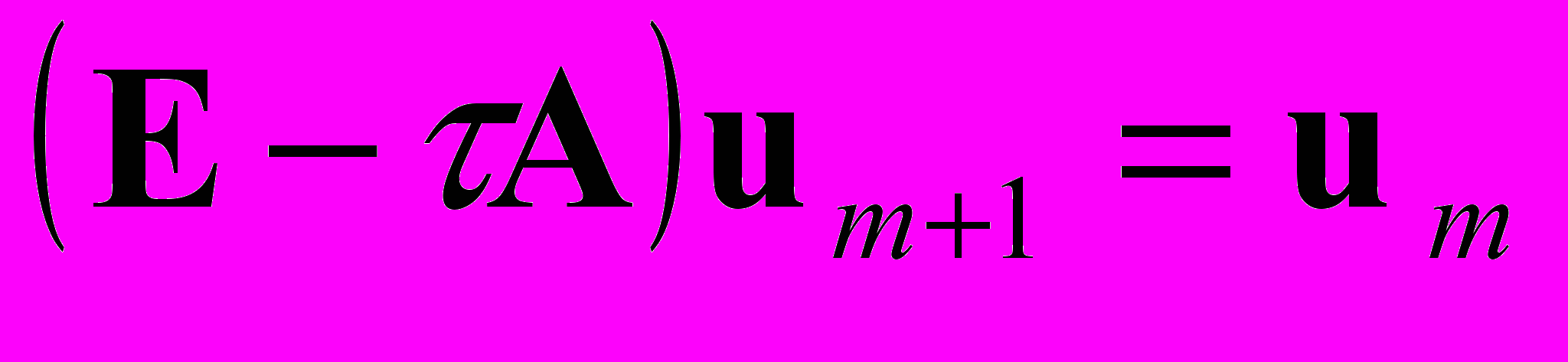 (12)
(12)и схеме Кранка-Николсона
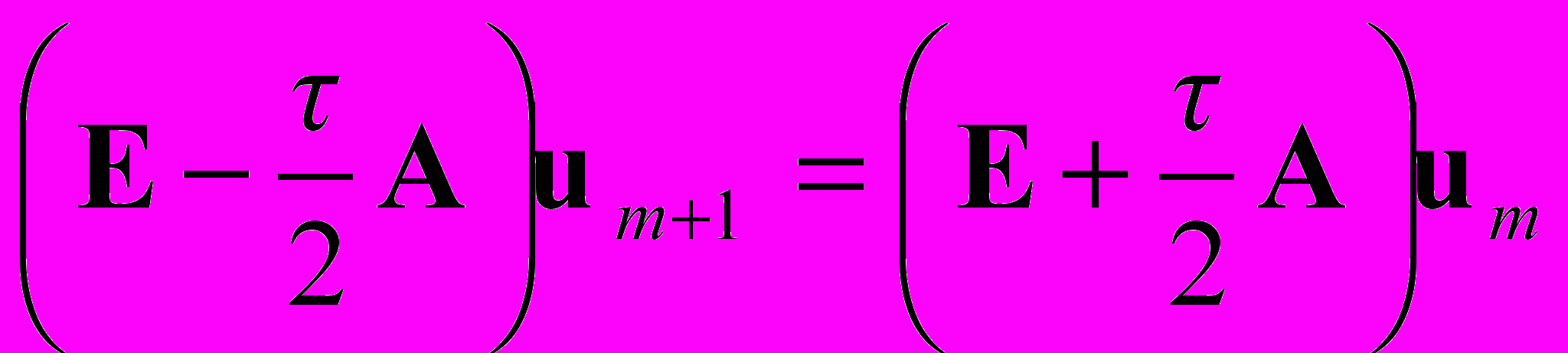 . (13)
. (13)Обе схемы являются абсолютно устойчивыми и требуют для расчета одного шага по времени решения системы линейных алгебраических уравнений с трехдиагональной матрицей. Схема (12) имеет первый порядок точности по времени, схема (13) – второй.
Для получения схем более высокого порядка применим к интегрированию системы (11) методы (5)–(7), для которых расчет временного шага приводит к решению систем линейных алгебраических уравнений:
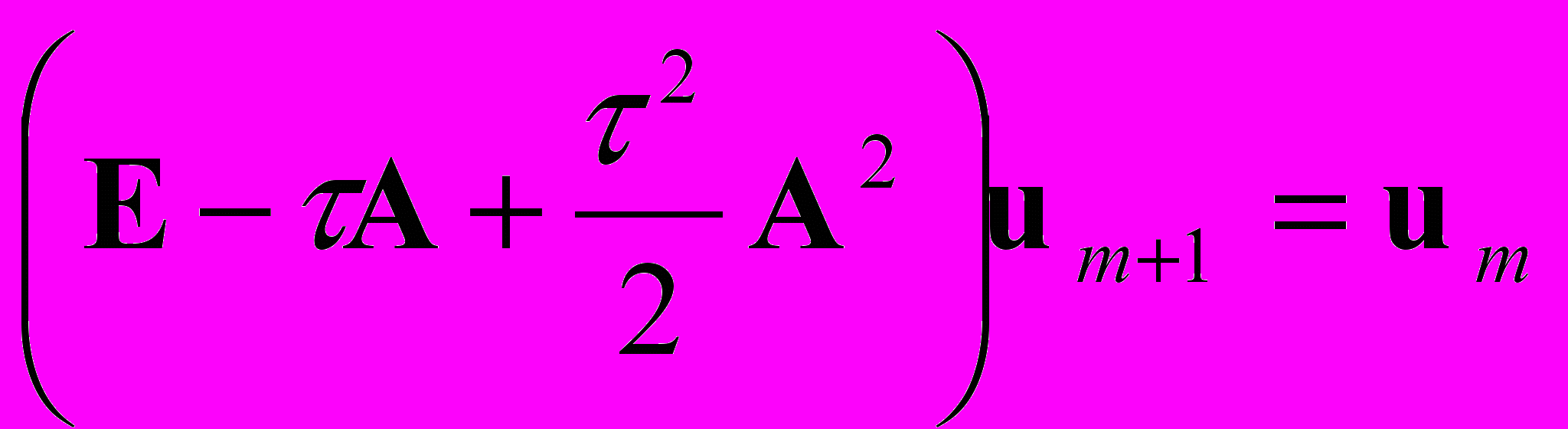 , (14)
, (14)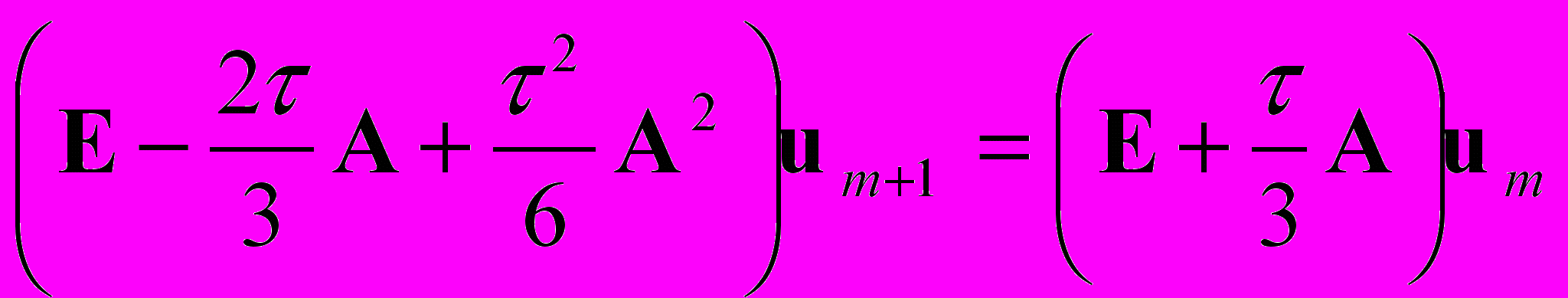 , (15)
, (15)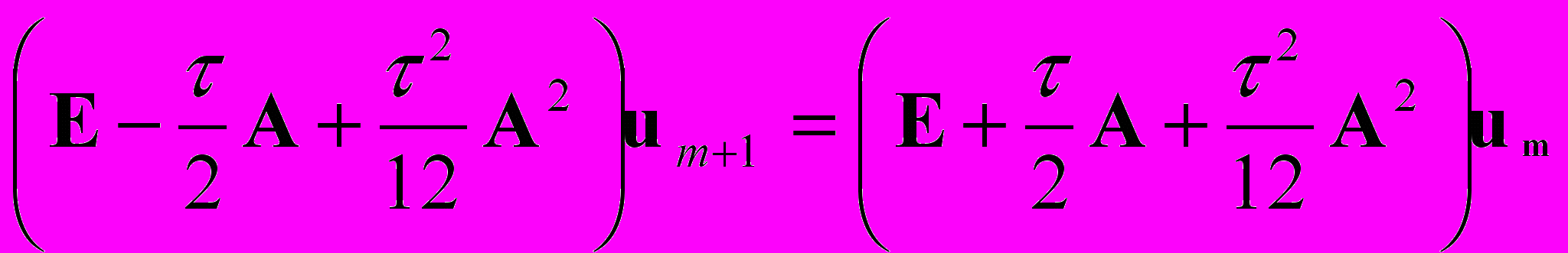 . (16)
. (16)Легко проверяется абсолютная устойчивость этих схем при интегрировании уравнения теплопроводности. Схемы имеют разный порядок точности по времени: соответственно второй, третий и четвертый. Все три схемы являются одношаговыми (двухслойными), имеют одинаковую трудоемкость, однако в отличие от схем (12), (13) требуют на шаге интегрирования решения линейной системы с пятидиагональной матрицей. Для решения систем с пятидиагональной матрицей можно использовать модификацию метода прогонки, которая требует для системы из N уравнений 21N арифметических операций (по сравнению с 8N операций при решении трехдиагональной системы). Таким образом, вычислительная трудоемкость схем (14) – (16) невелика по сравнению с неявной схемой или схемой Кранка-Николсона.
Для тестирования рассматриваемых схем были отобраны жесткие задачи, использованные в работах [3; 6; 7].
Схемы были апробированы на жесткой задаче
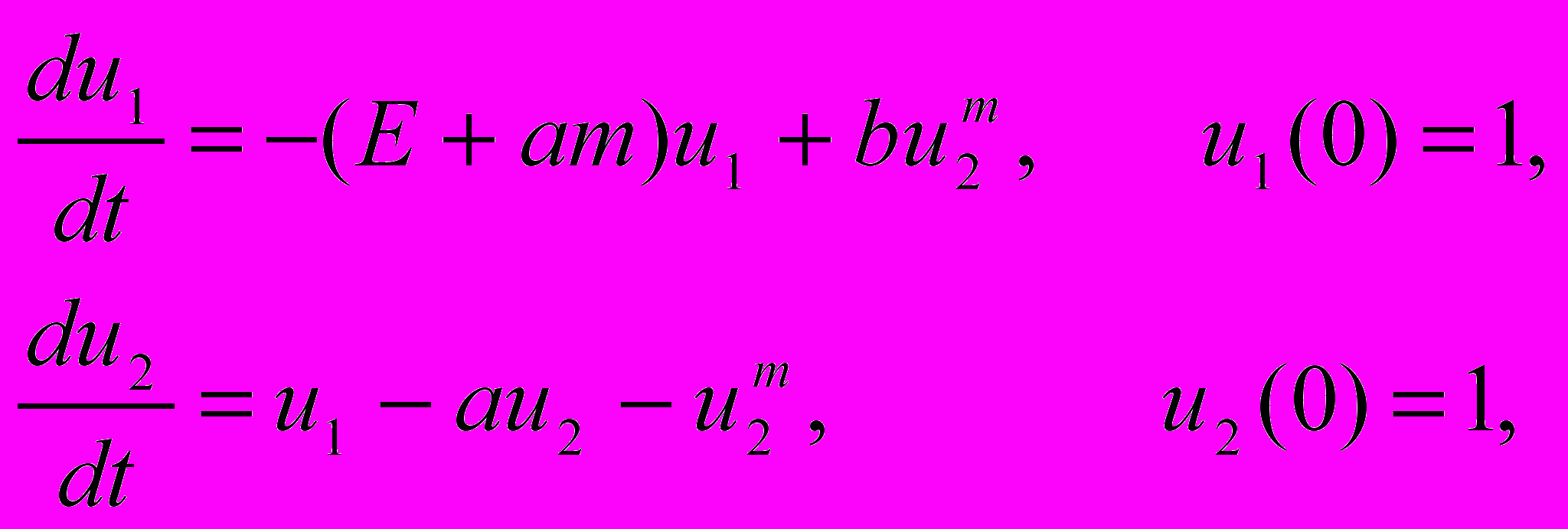 (17)
(17)с точным решением
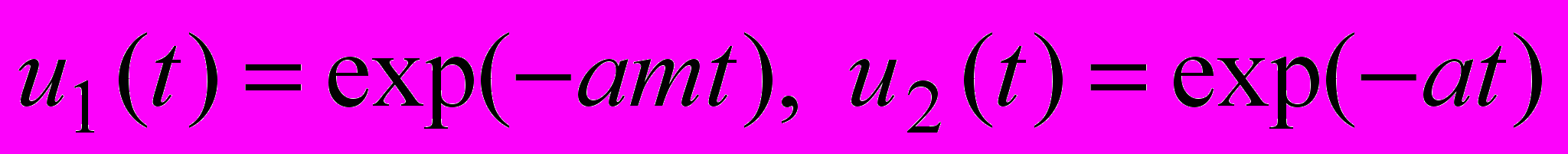 . Жесткость задачи определяется величиной числового параметра Е. При значениях a = 1, m = 2 система (17) соответствует известной тестовой задаче Капса. Данный тест интересен тем, что некоторые многостадийные диагонально-неявные схемы имеют на этой задаче эффективный порядок точности ниже теоретического, причем для случая средней жесткости.
. Жесткость задачи определяется величиной числового параметра Е. При значениях a = 1, m = 2 система (17) соответствует известной тестовой задаче Капса. Данный тест интересен тем, что некоторые многостадийные диагонально-неявные схемы имеют на этой задаче эффективный порядок точности ниже теоретического, причем для случая средней жесткости.Целью теста являлось определение скорости сходимости схем при уменьшении шага, а также подтверждение реального порядка точности данных схем в зависимости от жесткости задачи. Реальный порядок точности определялся по формуле:
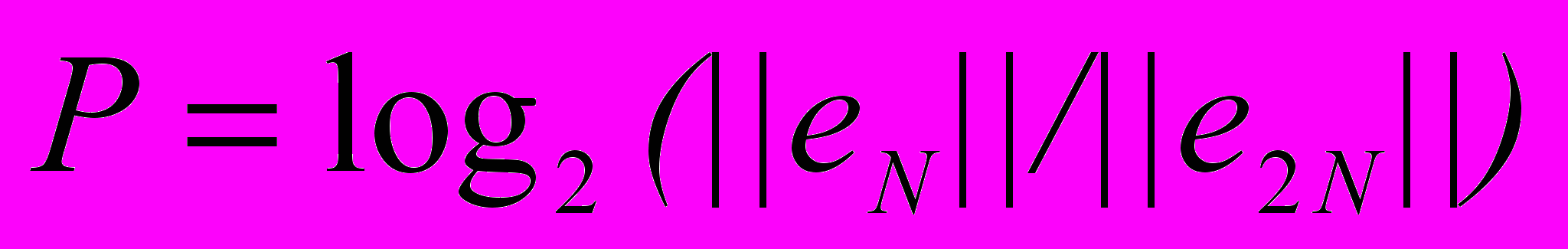 ,
,где ||eN||, ||e2N|| - евклидова норма абсолютной погрешности в конце интервала [0, 1] при интегрировании с шагом
 = 1/N и с шагом
= 1/N и с шагом  = 1/(2N) , где N – число временных шагов. Условие сходимости итераций при расчете временного шага принималось следующее: относительная погрешность двух последовательных итераций по модулю меньше 10-6 .
= 1/(2N) , где N – число временных шагов. Условие сходимости итераций при расчете временного шага принималось следующее: относительная погрешность двух последовательных итераций по модулю меньше 10-6 .Результаты тестирования представлены в таблицах 1 (для a = 1, m = 2) и 2 (для a = 1, m = 3) значениями евклидовой нормы абсолютной погрешности ||eN|| в точке t = 1, величины эффективного порядка точности P и общего числа решений систем итерационного решения шага на интервале интегрирования K для различных значениях параметра жесткости и шага интегрирования.
Таблица 1
| Схема второго порядка (8) | |||||||||||||||||||
| E | N=15 | N=30 | N=60 | N=120 | |||||||||||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||eN|| | K | P | |||||||||
| 10 102 103 104 108 | 4.38*10-4 3.34*10-4 3.23*10-4 3.22*10-4 3.22*10-4 | 47 45 45 45 45 | 1.13*10-4 8.58*10-5 8.28*10-5 8.25*10-5 8.25*10-5 | 90 90 90 90 90 | 1.95 1.96 1.96 1.96 1.96 | 2.89*10-5 2.18*10-5 2.10*10-5 2.09*10-5 2.09*10-5 | 180 180 180 180 180 | 1.97 1.98 1.98 1.98 1.98 | 7.30*10-6 5.49*10-6 5.27*10-6 5.26*10-6 5.25*10-6 | 240 360 360 360 360 | 1.98 1.99 1.99 1.99 1.99 | ||||||||
| Схема третьего порядка (9) | |||||||||||||||||||
| E | N=15 | N=30 | N=60 | N=120 | |||||||||||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||eN|| | K | P | |||||||||
| 10 102 103 104 108 | 3.51*10-6 2.03*10-6 1.86*10-6 1.85*10-6 1.85*10-6 | 45 45 45 45 45 | 4.46*10-7 2.57*10-7 2.35*10-7 2.30*10-7 2.33*10-7 | 90 90 90 90 90 | 2.98 2.98 2.98 3 2.99 | 5.63*10-8 3.24*10-8 2.96*10-8 2.93*10-8 2.93*10-8 | 180 180 180 180 180 | 2.99 2.99 2.99 2.97 2.99 | 7.09*10-9 4.06*10-9 3.72*10-9 3.68*10-9 3.68*10-9 | 360 360 360 360 360 | 2.99 2.99 2.99 2.99 2.99 | ||||||||
| Схема четвертого порядка (10) | |||||||||||||||||||
| E | N=15 | N=30 | N=60 | N=120 | |||||||||||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||eN|| | K | P | |||||||||
| 10 102 103 104 108 | 3.79*10-8 1.56*10-8 1.29*10-8 1.26*10-8 1.25*10-8 | 45 45 45 45 45 | 2.37*10-9 9.72*10-10 8.04*10-10 7.87*10-10 7.84*10-10 | 90 90 90 90 90 | 4 4 4 4 4 | 1.48*10-10 6.10*10-11 5.05*10-11 4.94*10-11 4.93*10-11 | 180 180 180 180 180 | 4 4 4 4 4 | 9.35*10-12 3.87*10-12 3.21*10-12 3.15*10-12 3.14*10-12 | 360 360 360 360 360 | 3.98 3.98 3.98 3.97 3.97 | ||||||||
Таблица 2
| Схема второго порядка (8) | |||||||||
Е | N=10 | N=20 | N=40 | ||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||
| 102 104 108 | 6.73*10-4 6.15*10-4 6.15*10-4 | 40 30 30 | 1.75*10-4 1.60*10-4 1.60*10-4 | 66 60 60 | 1.94 1.94 1.94 | 4.48*10-5 4.06*10-5 4.06*10-5 | 120 120 120 | 1.97 1.98 1.98 | |
| Схема третьего порядка (9) | |||||||||
Е | N=10 | N=20 | N=40 | ||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||
| 102 104 107 | 7.16*10-6 5.39*10-6 5.37*10-6 | 40 30 30 | 9.13*10-7 6.83*10-7 6.80*10-7 | 64 60 60 | 2.97 2.98 2.98 | 1.16*10-7 8.59*10-8 8.56*10-8 | 120 120 120 | 2.98 2.99 2.99 | |
| Схема четвертого порядка (10) | |||||||||
E | N=10 | N=20 | N=40 | ||||||
| ||eN|| | K | ||eN|| | K | P | ||eN|| | K | P | ||
| 102 104 107 | 1.20*10-7 5.58*10-8 5.52*10-8 | 40 30 30 | 7.37*10-9 3.49*10-9 3.45*10-9 | 61 60 60 | 4.02 4.00 4.00 | 4.60*10-10 2.19*10-10 2.16*10-10 | 120 120 120 | 4.00 3.16 4.00 | |
Результаты тестирования показали, что каждая из схем подтвердила свой порядок точности на всем диапазоне изменения параметра жесткости Е. При этом среднее количество итераций для всех схем за период интегрирования практически не зависело от величины шага и составляло в среднем 3. Сравнение показывает, что на данных тестах точность результатов схем лучше с увеличением их порядка и не чувствительна к ухудшению свойств устойчивости. В частности лучшие результаты показывает А-устойчивая схема четвертого порядка (10).
Одним из тестов, считающихся наиболее трудным для методов интегрирования жестких систем, является оссцилятор Ван-дер-Поля, моделируемый системой уравнений
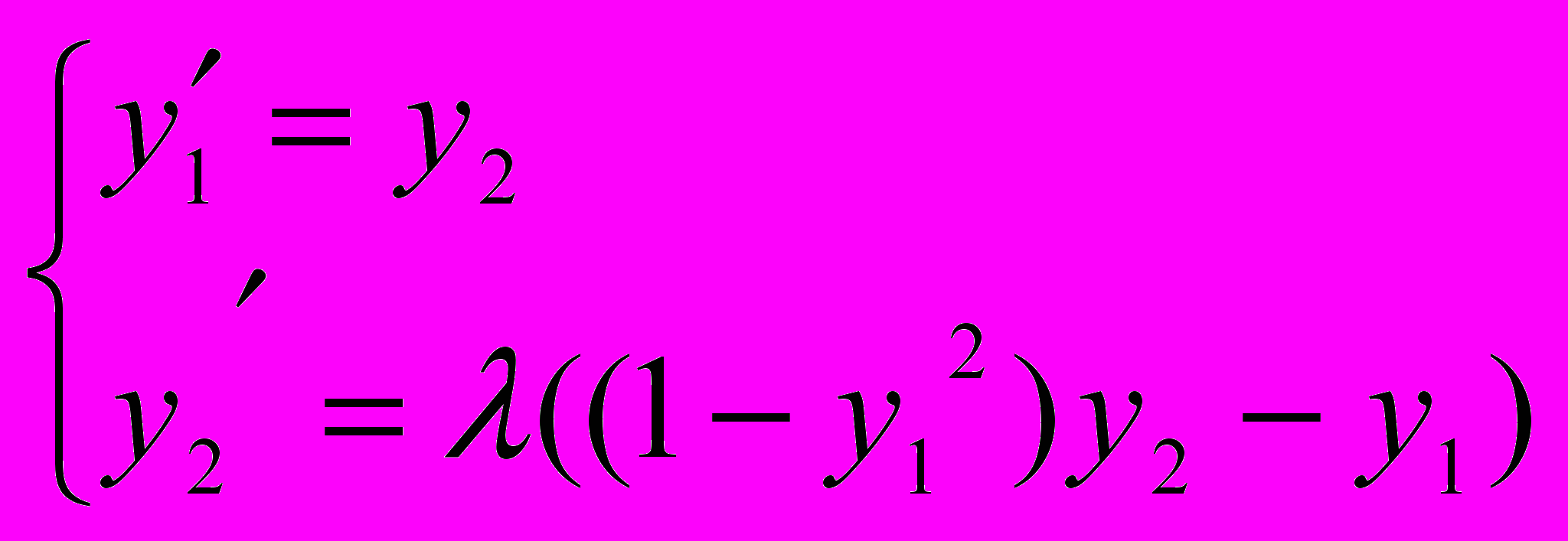 , (18)
, (18)в которой для параметра
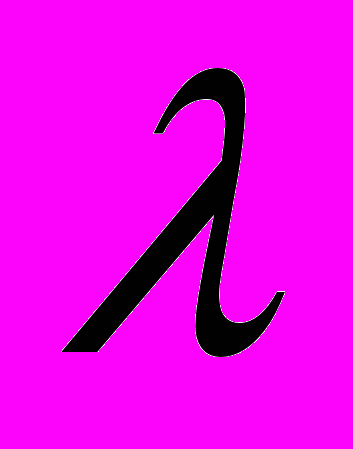 характерны большие числовые значения. Для величины
характерны большие числовые значения. Для величины 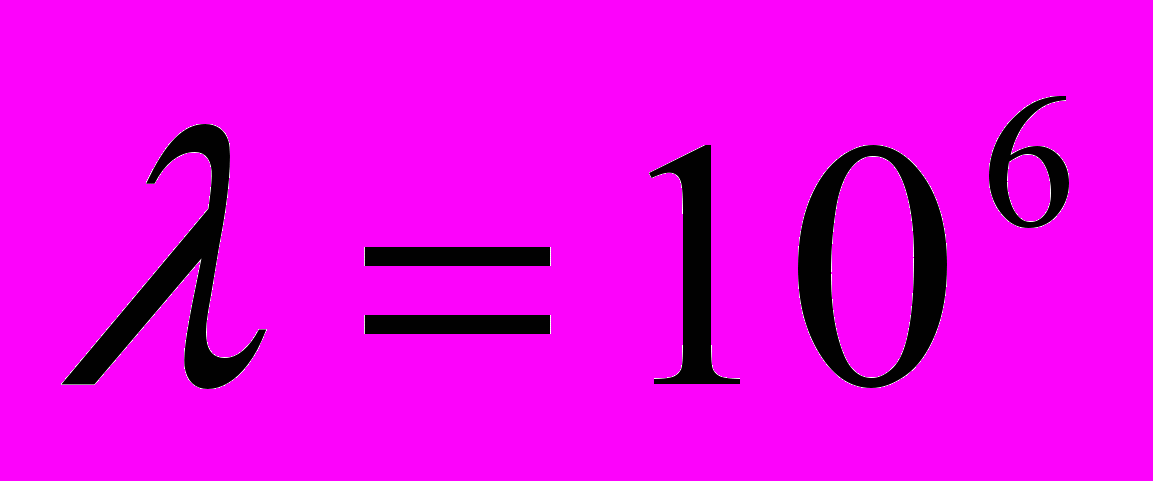 и начальных условиях
и начальных условиях 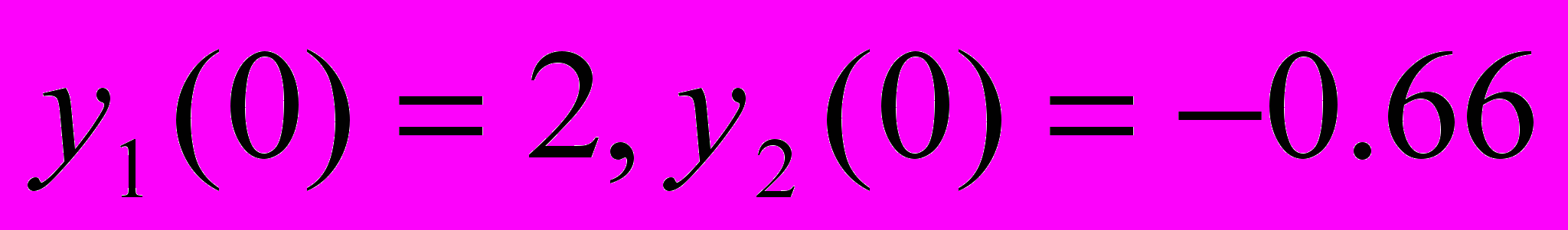 , принятых в качестве исходных данных в [3], нами были протестированы все три схемы. При решении использовалась процедура оценки погрешности и корректировки шага интегрирования по методу двойного пересчета [3, 9]. При этом максимально допустимый рост величины шага интегрирования ограничивался коэффициентом 2.5.
, принятых в качестве исходных данных в [3], нами были протестированы все три схемы. При решении использовалась процедура оценки погрешности и корректировки шага интегрирования по методу двойного пересчета [3, 9]. При этом максимально допустимый рост величины шага интегрирования ограничивался коэффициентом 2.5. При проведении тестов отслеживалось количество вычислений правой части системы и матрицы Якоби (Ncomp) (в данных схемах эти величины одинаковы), а также число выполненных шагов (Nstep) и отброшенных шагов (Dstep). Кроме того, анализировалось правильное воспроизведение решения, в частности соответствие периодичности изменения каждой компоненты решения. Результаты тестирования приведены в таблице 3 для относительной погрешности
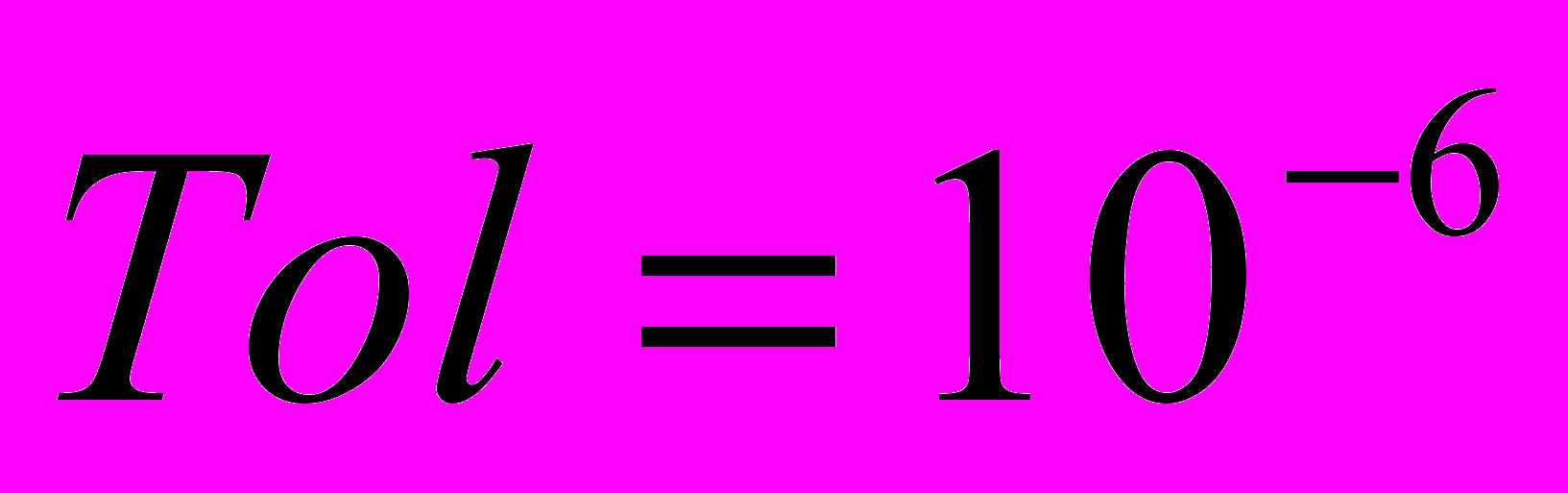 .
.Таблица 3
| Схемы | Ncomp | Nstep | Dstep |
| (8) | 37912 | 4778 | 346 |
| (9) | 11594 | 1080 | 235 |
| (10) | 6753 | 469 | 273 |
Предварительный анализ, иллюстрируемый данными таблицы 3, показал преимущество схем более высокого порядка по объему вычислений при решении задачи.
В то же время сопоставление решений, получаемых с помощью исследуемых схем с решением, приведенным в работе [3], показал, что только схема второго порядка (8) дает правильную периодичность изменения компоненты, в то время как схема третьего порядка дает результаты соответствующие увеличению истинного периода примерно на 10%. Схема четвертого порядка дает решение с еще большим искажением периода (рис. 1а).
Из анализа изменения величины шага (рис. 1б) видно, что схемы третьего и четвертого порядка «проскакивают» момент резкого изменения решения и начинают уменьшать шаг с опозданием. Кроме того, для схемы (10) характерны циклы резкого уменьшения шага в период плавного изменения решения, отсутствующие у схем (8) и (9). Учитывая положительные результаты предыдущих тестов, возможной причиной неудачных результатов схем (9) и (10) на задаче Ван-дер-Поля может быть неэффективность процедуры оценки погрешности в методе двойного пересчета для схем (9), (10) на подобном типе задач.
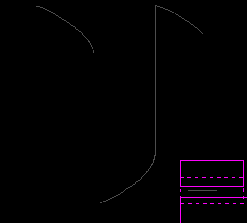
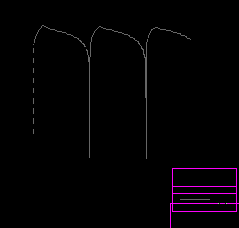
а) б)
Рис. 1. Расчетные значения компоненты y1(t) (а) и величина шага интегрирования (б) при решении задачи Ван-дер-Поля схемами (8)-(10).
Апробация схем (14)-(16) для уравнения теплопроводности проводилась на двух задачах с известными точными решениями. По результатам решения сопоставлялась величина равномерной погрешности, получаемой в период решения с использованием данных схем и схем (12), (13), при различных значениях пространственного (h=1/N) и временного (τ=1/M) шагов.
Результаты решения задачи с непрерывными данными, определяемой условиями
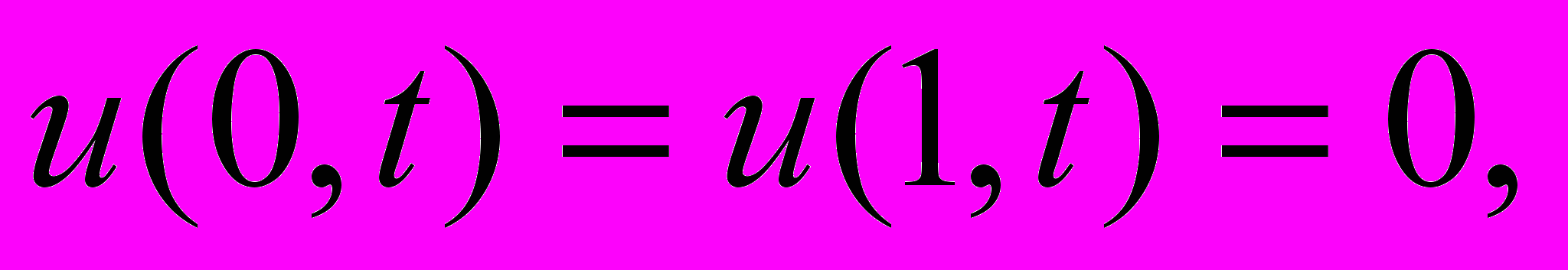
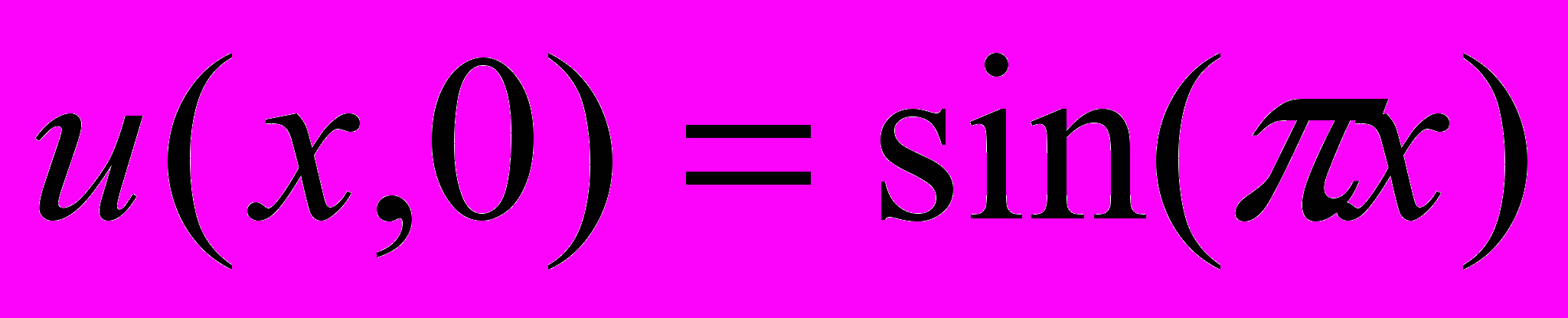 и имеющей точное решение
и имеющей точное решение 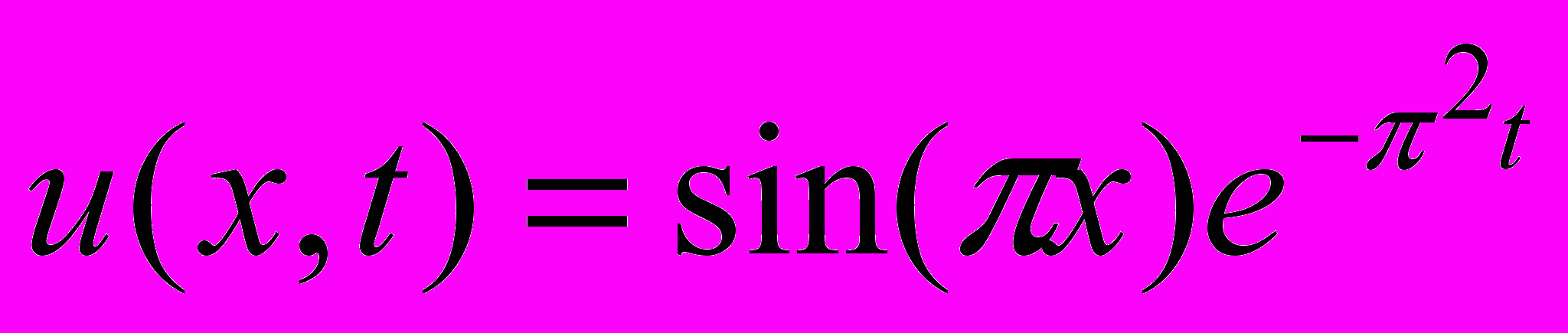 приведены в таблице 4. При сопоставлении результатов для разных параметров сеток учитывался различный порядок аппроксимации схем по пространству и по времени. Схема второго порядка (14) дает сопоставимые, но несколько худшие результаты по сравнению со схемой Кранка-Николсона (13). Точность схем (15) и (16) значительно выше на густых сетках при больших величинах временного шага.
приведены в таблице 4. При сопоставлении результатов для разных параметров сеток учитывался различный порядок аппроксимации схем по пространству и по времени. Схема второго порядка (14) дает сопоставимые, но несколько худшие результаты по сравнению со схемой Кранка-Николсона (13). Точность схем (15) и (16) значительно выше на густых сетках при больших величинах временного шага.Таблица 4
| Схемы | N  M MПогрешность для задачи с непрерывными данными | N  M MПогрешность для задачи с разрывными данными | ||||
| (12) | 10  10 100.1326 | 20  40 400.0439 | 40  80 800.2176 | 20  20 200.0277 | 40  80 800.0157 | |
| (13) | 10  10 100.0299 | 20  20 200.0069 | 40  40 400.0017 | 20  20 200.0079 | 40  40 400.0020 | 80  80 800.0006 |
| (14) | 10  10 100.0341 | 20  20 200.0113 | 40  40 400.0033 | 20  20 200.00572 | 40  40 400.00296 | 80  80 800.00103 |
| (15) | 10  10 100.00096 | 20  20 200.00022 | 40  20 200.00022 | 20  20 200.00103 | 40  40 400.00019 | 80  40 400.00101 |
| (16) | 10  10 100.00352 | 40  20 200.00019 | 80  40 400.00001 | 20  20 200.00072 | 80  40 400.00009 | 80  80 800.00001 |
Для задачи с условиями
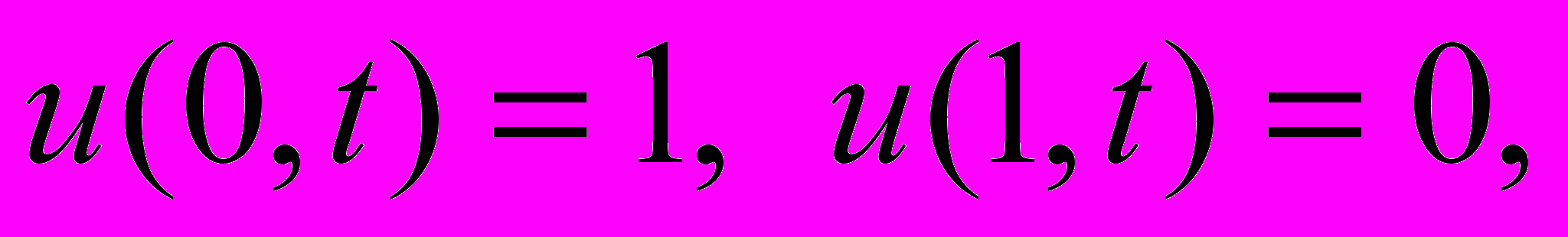
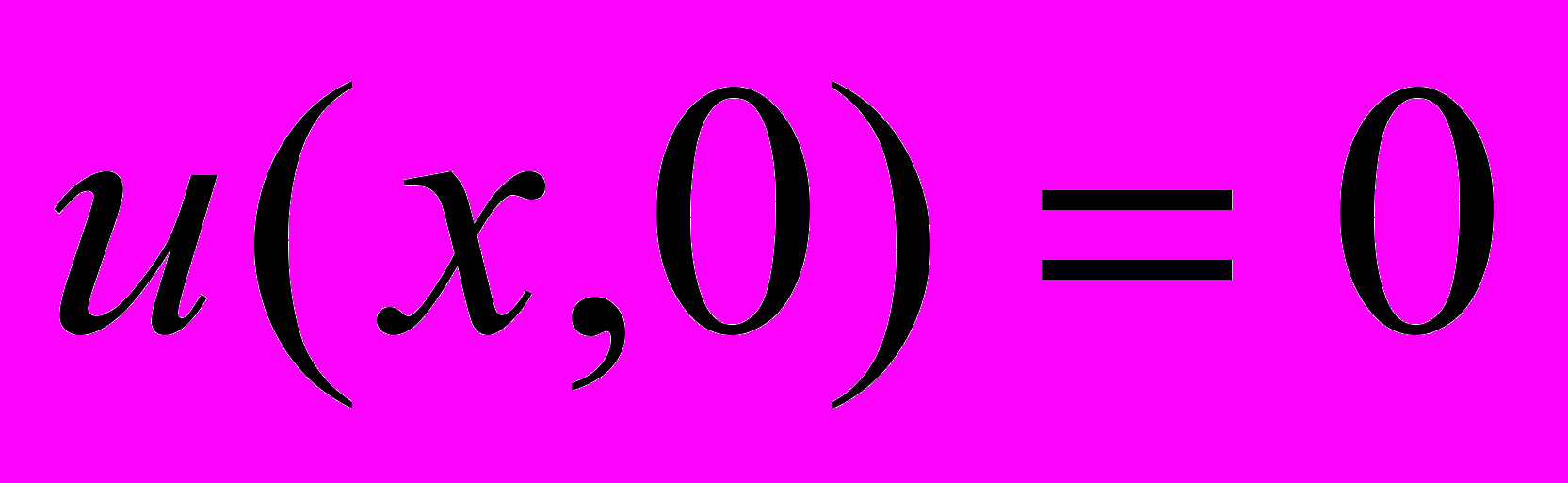 характерна разрывность входных данных в точке (x=0, t=0). Расчет этой задачи показывает чувствительность схем (13) и (16) к разрывному характеру входных данных и большие отклонения от точного решения на первых временных шагах. У схем (14) и (15) наблюдались наименьшие отклонения в указанные моменты. Эксперименты показали, что схемы высокого порядка можно эффективно использовать в случае задания на малый момент времени сглаженных условий, в качестве которых задавалось распределение из точного решения. Соответствующие результаты приведены в таблице 4.
характерна разрывность входных данных в точке (x=0, t=0). Расчет этой задачи показывает чувствительность схем (13) и (16) к разрывному характеру входных данных и большие отклонения от точного решения на первых временных шагах. У схем (14) и (15) наблюдались наименьшие отклонения в указанные моменты. Эксперименты показали, что схемы высокого порядка можно эффективно использовать в случае задания на малый момент времени сглаженных условий, в качестве которых задавалось распределение из точного решения. Соответствующие результаты приведены в таблице 4.Общий вывод по апробации схем (14)–(16) на решении задач для уравнения теплопроводности показывает на предпочтительность применения схем более высокого порядка по времени для получения решений с высокой точностью при соблюдении достаточной гладкости входных данных.
Проведенные сопоставительные эксперименты на целом ряде задач-тестов показали, что все предлагаемые схемы показали положительные результаты по сходимости и устойчивости, что дает основание рекомендовать их использование при решении жестких задач. Предложенная итерационная процедура расчета временного шага, подтвердившая свою эффективность на всех задачах-тестах, дает возможность построения малозатратных вычислительных алгоритмов на основе схем высокого порядка с учетом производных от правых частей. Показательным результатом сравнительной апробации является то, что схема четвертого порядка точности оказалась в целом более эффективной, несмотря на то, что ее характеристики устойчивости (А-устойчивая) более слабые, чем у схемы второго порядка точности (L2-устойчивая), за исключением расчетов осциллятора Ван-дер-Поля с контролем погрешности и выбором шага, результаты которых требуют дополнительного исследования.
ЛИТЕРАТУРА
- Оран Э., Борис Дж. Численное моделирование реагирующих потоков. – М.: Мир, 1990.
- Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких нелинейных дифференциальных уравнений. – М.: Мир, 1998.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир, 1999.
- Широбоков Н. В. Диагонально-неявные схемы Рунге-Кутты// Ж. вычисл. Матем. И матем. Физ. – 2002. – Т. 42, №7. – С. 1013-1018.
- Калиткин Н.Н. Численные методы решения жестких систем // Математическое моделирование. – 1995. – Т. 7, № 5. – С. 8-11.
- Кочетков К. А., Ширков П. Д. В-сходимость L-затухающих ROW-методов// Сб. научн. Тр. СурГУ. Вып. 4. – Сургут: СурГУ, 1998. – С. 44-53.
- Скворцов Л. М., Диагонально-неявные FSAL-методы Рунге-Кутты для жестких и дифференциально-алгебраических систем // Матем. моделирование, 2002. – Т.14, N2. – С. 3-17.
- Сигунов Ю.А. Об одном классе неявных методов интегрирования жестких систем дифференциальных уравнений // Пути обновления педагогического образования: Труды СурГПИ. Выпуск 1. – Сургут: РИО СурГПИ, 2003. – С. 141-145.
- Калиткин Н.Н. Численные методы. – М.: Наука, 1978.
