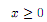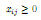Курсовой проект по дисциплине: Теория информационных процессов и систем на тему: Теория транспортных сетей с различными транспортными издержками. Поиск оптимальных маршрутов снабжения

1   2   3   4   5

Задача 2

На складах A1, A2, A3 хранится a1=100, a2=200, a3=120 едениц одного того же груза соответственно. Требуется доставить его трем потребителям B1, B2, B3, заказы которых составляют b1=200, b2=110, b3=80 едениц груза. Стоимость перевозки Ci,j единицы груза с i – склада j – ому потребителю указаны в транспортной таблице:

	b1=200	b2=110	b3=80
a1=100	4	2	6
a2=200	7	5	3
a3=120	1	7	6

Найти минимальную стоимость перевозок.

Для этого, сверх имеющихся n пунктов назначения b₁, b₂, b₃,введём ещё один, фиктивный, пункт назначения b₄, которому припишем фиктивную заявку, равную избытку запасов над заявками. А стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения b₄ будем считать равным нулю. Введением фиктивного пункта назначения B ₄ с его заявкой b ₄ мы сравняли баланс транспортной задачи и теперь его можно решать как обычную транспортную задачу с правильным балансом. (количество перевезенного груза обозначим символами x1….xn соответственно)

	b1 = 200	b2 = 110	b3 = 80	b4 = 30
a1 = 100	4 x1	2 x2	6 x3	0 x4
a2 = 200	7 x5	5 x6	3 x7	0 x8
a3 = 120	1 x9	7 x10	6 x11	0 x12

Задаем начальные значения X.


З
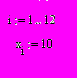
адаем общую стоимость перевозок:





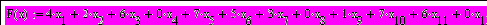
Задаем условия:





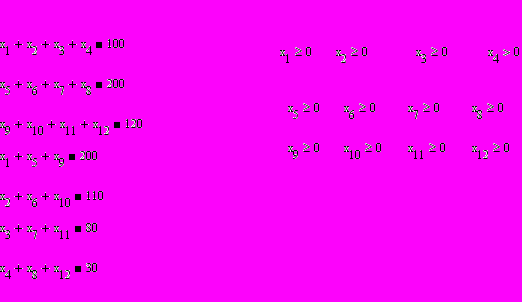
Используя встроенную функцию Mimimize, находим значения x1…x12 при которых F(x) будет минимальным.






Находим минимальную стоимость перевозки:


Р
езультаты заносим в транспортную таблицу:

	b1=200	b2=110	b3=80
a1=100	4	2 x2 =100	6
a2=200	7 x5 = 80	5 x6 = 10	3 x7 = 80
a3=120	1 x9 =120	7	6

Минимальная стоимость перевозок: F = 1170.

Задача 3

В некотором царстве, некотором государстве жил-был кот Василий, который очень любил мышей… на обед. А обедал он исключительно в амбаре своего хозяина, да так хорошо, что бедные мыши и носу не могли высунуть из своих нор. Но всю жизнь в норе не просидишь, есть то хочется, и стали мыши думать и гадать, как им провести кота Василия и до заветных пищевых ресурсов амбара добраться.

В амбаре было 5 мышиных нор: в первой проживало 15 мышей, во второй – 20, в третьей – 10 мышей, в четвертой – 25 мышей, а в пятой – 5 мышей а также 3 источников пищи, от которых и кормилась вся эта орава мышей: у мешка крупы – 24 мышей, у мешка муки – 19 мышей, и у стопки старых газет и журналов – 17 мышей.

И тут мыши вспомнили, что когда-то в стопке журналов лежала книжка по математическому программированию. Конечно мыши давным-давно успели ее сгрызть, но кое-что из нее они, пока грызли, прочитать успели, в частности, как решать транспортные задачи.


Рассмотри более подробно задачу выбора маршрута


Источники пиши

А = 41; В = 36; С = 18; всего 95.

Потребность

а = 20; b = 30; с = 20; d = 35; е = 15; всего 120.

Безусловно, цель мышей – добраться до еды с минимальными потерями по дороге.

Вопрос:

Как организовать ежедневные пути так, чтобы общая сумма транспортных издержек была минимальной? Объем пищи и потребности в изменяются ото дня ко дню, задачу приходится решать ежедневно.


Ответ:

Ответом на поставленный вопрос будет решение задачи в программе

MathCad.


Необходимо, конечно, оценить и выгодность передвижения из каждой норы к каждому пищевому ресурсу. Для этого мыши оценили так называемые потенциалы нор и источников пищи. Так как их цель – минимизировать потери, то сумма потенциалов в каждом случае не должна превышать затрат.

Мыши с помощью таблицы указали число попавших в лапы кота (в процентах) по отношению к общему числу мышей из 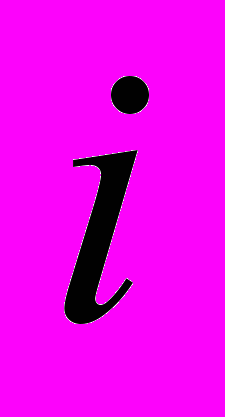-той норы, питающихся у 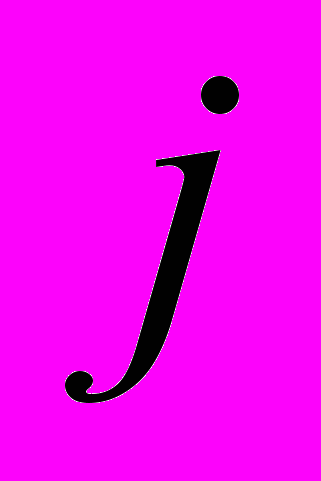-того источника пищи. Эти данные они также записали в виде матрицы (в относительных единицах):

.


Поскольку потребности превосходят объем источников, введем фиктивный источник пищи F, для которого транспортные расходы окажутся гораздо более высокими, чем расходы для фактически имеющихся источников.

Таким образом, в условиях оптимального окончательного решения, фиктивный источник должен будет выпускать ровно 25 источников пищи. Пусть фиктивные издержки по транспортировке составляют 50.

Для этого достаточно сделать так, чтобы суммы величин, находящихся в строках, были бы равны соответствующим наличным объемам, а суммы величин в каждом столбце - потребностям соответствующего склада. Однако нет никакого основания утверждать, что это решение, в сущности, совершенно произвольное, является наилучшим, т. е. что оно обеспечивает минимизацию транспортных расходов. Ведь число всех возможных решений так велико! Как же поступить?




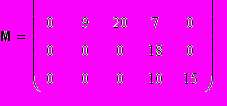
В таблице с т строками и п столбцами, оптимальное решение обязательно должно содержать не менее чем (m - 1) (n - 1) нулей.

Оптимальные решения составляют часть множества всех решений, содержащих не более (m - 1) (n - 1) нулей. С помощью базисного решения, можно последовательно уменьшить общие издержки, выбирая при этом решения, содержащие не менее (m - 1) (n - 1) нулей каждое. В результате мы придем к оптимальному решению.

Рассмотрим базисное решение. Будем, начинать с северо-западного угла (обозначенного стрелкой), заполнять первую строку, насыщая последовательно столбцы а и b; запишем далее остаток запаса в первую клетку столбца с. Насытим затем столбец с, строку В, столбец d, строку С и, наконец, столбец е. Строка F окажется при этом насыщенной автоматически.

Для улучшения решения займемся рассуждениями в духе маргинальной теории.

Рассчитаем издержки от производства к потребителю




Вычислим маргинальную матрицу



Далее выберем наилучшее маргинальное решение

Мы видим, что маргинальная затрата составила -0,07.

Таким образом, мы получаем следующую матрицу, для которой общие затраты уменьшились.


Затраты, составят




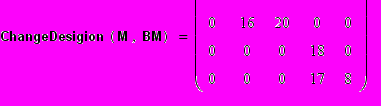
Далее воспользуемся FindBestDecision, который находит наилучшее маргинальное решение и изменяет исходное:


-Находит наилучшее маргинальное решение и изменяет исходное. Повторяет процесс, пока есть хорошие маргинальные решения.

Возвращает вектор:

1-й элемент - наилучшее решение;

2-й - стоимость, жизни.











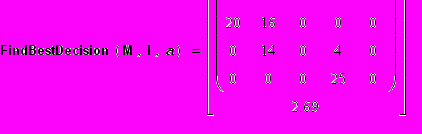
Порассуждав таким образом, мыши получили следующий начальный опорный план:


Оптимальные маршруты:

Стоимость жизни: (без учета фиктивных источников пищи)


По этому опорному плану коту достанется 3 мыши (0,31 часть мыши отдельно вряд ли выживет).


Это оптимальное решение не является единственным, потому что имеется маргинальная нулевая затрата и всякое изменение приведет к другому решению, для которого общие затраты будут такими же.

Это распределение касается только данного дня. Следовательно, каждый день расчет нужно проводить вновь.

Заключение

Транспортные задачи являются основными задачами для некоторых отраслей промышленности (нефтяной, черной металлургии и т. д.).

Транспортная задача является представителем класса задач линейного программирования и поэтому обладает всеми каче­ствами линейных оптимизационных задач. Одновременно она имеет и ряд дополнительных полезных свойств, которые позво­лили разработать специальные методы ее решения.

Первый точный метод решения Т-задачи разработан Л. В. Канторовичем и М. К. Гавуриным. Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

Данный курсовой проект способствует приобретению навыков самостоятельного применения теоретических знаний к решению практических задач по исследованию систем, а именно транспортных задач. Исследовав способы решения однотипных транспортных задач, можно прийти к выводу, что метод Фогеля наиболее предпочтителен, т.к. дает оптимальный вариант. Разработанная система в пакете MathCad позволяет решить любую похожую задачу оптимизации (по цене, времени или др.фактору) перевозок.

Итак, решая поставленные транспортные задачи, мы максимально удовлетворили требованиям по доставке, установили оптимальное распределение потоков грузов. Однако, иногда полностью удовлетворить требования всех заказчиков не удаётся, что в принципе бывает и не возможно, учитывая условия задачи, кажущиеся первоначально вполне выполнимыми.

Конечно, в реальной жизни существуют более сложные транспортные сети, с большим количеством различных условий, факторов, связей, и оптимизировать поток такой системы гораздо сложнее. Для разрешения таких проблем существует специальный социально-этический вид маркетинга, позволяющий выбрать наиболее эффективный вариант с учетом всех ограничений, связанных с интересами потребителей, поставщиков и общества.

Литература

1. Горяцев Л.В. Задачи линейного программирования транспортного типа, Учебно-методическое пособие, Владивосток: Издательство Дальневосточного университета, 2003. – 16 с.
   

2. Вентцель Е.С. Введение в исследование операций, М.: Издательство «Советское радио», 1964. – 391 с.
   

3. Таха, Хедми А. Введение в исследование операций, 7-е издание.: Пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 912 с.
   

4. Кофман А. Займемся исследованием операций, М.: Издательство «МИР», 1966. – 280 с.