Оптимизация технологических параметров тампонажных завес городских подземных сооружений на основе теории риска 25. 00. 22 «Геотехнология (подземная, открытая и строительная)»
| Вид материала | Автореферат диссертации |
- Обоснование рациональных параметров чугунно-бетонной крепи вертикальных стволов 25., 239.1kb.
- Обоснование геотехнологических методов повышения экологической безопасности освоения, 284.69kb.
- Пособие по производству работ при устройстве оснований и фундаментов (к сниП 02. 01-83), 5989.06kb.
- Лекция №7 Тема: «Проектирование городских дорог», 151.63kb.
- Оптимизация технологических параметров скважинного подземного выщелачивания драгоценных, 318.75kb.
- Правила безопасности при строительстве подземных сооружений пб 03-428-02, 4437.54kb.
- Правила безопасности при строительстве подземных сооружений пб 03-428-02, 4281.3kb.
- Методические указания Николаева Т. Н., Усов В. А. «Инженерное мерзлотоведение». Методические, 164.37kb.
- Правила безопасности при строительстве метрополитенов и подземных сооружений с дополнениями, 3350.15kb.
- Вопросы по Технологии возведения зданий и сооружений. Пгс, 61.57kb.
Таблица 4
Коэффициенты корреляции зависимости 0 с vg, коэффициенты вариации
динамического напряжения сдвига и динамической вязкости суспензий «Микродура»
-
Состав,
В : М,
по весу
Коэффициенты корреляции зависимости
0 с vg
Коэффициенты
вариации
0
с
RF
0,75 : 1
0,903
0,227
0,132
1 : 1
0,913
0,107
0,140
1,5 : 1
0,931
–
0,108
2 : 1
0,932
–
0,132
RU
0,75 : 1
0,971
0,070
0,064
1 : 1
0,993
0,690
0,038
1,5 : 1
0,976
–
0,068
2 : 1
0,913
–
0,071
RX
0,75 : 1
0,948
0,041
0,101
1 : 1
0,992
0,041
0,040
1,5 : 1
0,986
0,133
0,049
2 : 1
0,990
0,143
0,036
3. Технологические параметры тампонажных завес
В диссертации выполнен вероятностный анализ мощности и глубины завес, радиусов инъекции, продолжительности, рабочих давлений и дебитов нагнетания для зажимного и циркуляционного (полуциркуляционного) способов, предельных давлений нагнетания, схем размещения тампонажных скважин, расстояний между скважинами, очередности нагнетания. Мерой эффективности принимаемых технических решений является уровень риска – вероятность получения негативного результата. Оценка уровней рисков выполнена по методу Монте-Карло (рис. 3).
В
ероятностный анализ мощности и глубины тампонажных завес проведен в диссертации по четырем известным моделям на примерах, отражающих конкретные гидродинамические ситуации: контурная совершенная завеса котлована (предварительный тампонаж напорного водоносного пласта), отвечающая гидродинамической схеме «большого колодца»; кольцевая завеса ствола (последующий тампонаж); линейная завеса совершенного типа (предварительный тампонаж в безнапорном водоносном пласте); линейная несовершенная завеса в напорном водоносном пласте. В рассматриваемых ситуациях влияние мощности и глубины завес определяется качеством завесы – величиной остаточного притока воды в подземное сооружение. Пример вероятностного анализа выполнен для схемы «большого колодца»:Q (2,7 h He) / (kт–1 lg (rт rп–1) k –1lg (R(t) rт–1) ); R(t) (a t)1/2; M rт–rп,
где Q – остаточный или допустимый приток воды в сооружение; h – глубина завесы; He – напор в водоносном пласте; rп – радиус «большого колодца» – приведенный внутренний радиус котлована (в плане) квадратной, прямоугольной или неправильной формы с соотношением длины к ширине менее 10 : 1: kт – коэффициент фильтрации затампонированных грунтов; k – коэффициент фильтрации грунтового массива; R(t) – радиус влияния дренажа выработки; a – коэффициент пьезопроводности; t – время от начала дренирования; M –мощность завесы.
В табл. 5. приведены исходные данные для вероятностного анализа с использованием нормального и Грамма-Шарлье распределений, в табл. 6 – полученные результаты. Варианты тампонажных завес с рисками затопления котлована менее 0,2, подлежащие экономическому анализу, в табл. 6 выделены курсивом. Детерминированное значение притока составляет 129,7 м3/сут.
Генерация входных случайных чисел, распределенных по закону Грамма-Шарлье, выполнена численным методом (скорость генерации 50 случайных чисел Rу в секунду) с использованием соотношений:
1 1 1 Rн
RуRнs
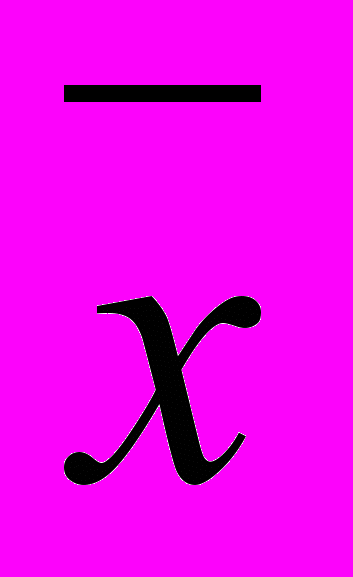; Rн–(1 (Rн))– ––A0(2)(Rн) ––E0(3)(Rн); (Rн) 2/2exp(–,5Rн2); 2 3! 4! 0
0(2(Rн) (Rн2– 1)0(Rн); 0(3)(Rн) –(Rн3–3Rн )0(Rн); 0(Rн) (2)–0,5exp(–0,5Rн2),
где
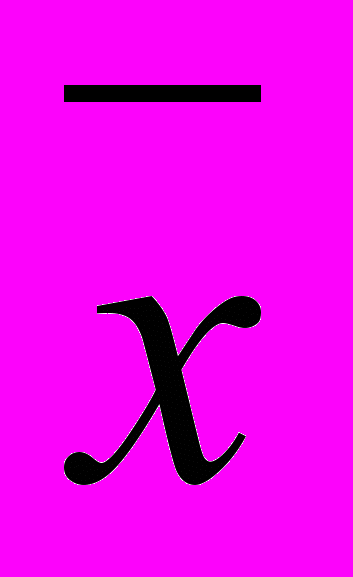, s, A, E – среднее выборочное, стандарт, асимметрия и эксцесс; Rн –равномерно распределенное случайное число, вырабатываемое датчиком ЭВМ.В целом результаты исследований мощности и глубины тампонажных завес, выполненные в условиях риска, позволяют сделать следующие выводы: 1 – водоприток через завесу уменьшается с возрастанием мощности завесы по гиперболической зависимости, поэтому повышение мощности завес не всегда является технически оправданным средством борьбы с обводнением городских подземных сооружений; 2 – существенное влияние на мощность завес оказывает качество тампонажа, выражающееся коэффициентом фильтрации протампонированной зоны. Следует отметить целесообразность применения суспензий «Микродур», разумеется, с учетом результатов экономического обоснования; 3 – устройство несовершенных завес с глубиной, составляющей 2/3 от мощности водоносного пласта, не обеспечивает приемлемого снижения водопритоков; 4 – эффективной мерой является повышение водонепроницаемости обделки объекта, в частности, для обделок вертикальных стволов снижение коэффициента фильтрации с 0,005 до 0,001 м/сут сопровождается уменьшением остаточных водопритоков в 1,8 4,8 раза.
Вероятностный анализ технологических параметров тампонажных завес выполнен для способов последовательного и группового нагнетания в режимах постоянного дебита, постоянного давления, боковой и донной схем нагнетания ньютоновских и неньютоновских тампонажных жидкостей в пористых и трещиноватых однородных и анизотропных грунтах. Особенности статистического моделирования технологических параметров тампонажа поясняются на модели бокового нагнетания вязко-пластичной жидкости в трещиноватый грунт, разработанной проф. И. И. Вахромеевым:
с Q R
P0 – PR –––– [ ––––– ln ––– B C1 (R – r0) ],
Kп 2 h r0
где – коэффициент, 81,6 / A; A – опытный коэффициент, 110 A 115; B 0 / с; C1 0,5 m b0; b0 – среднее раскрытие трещин, b0 4,83 (Kп m2,1)1/2; Kп – коэффициент проницаемости.
Исходные данные для вероятностного анализа указаны в табл. 7.
Таблица 5
Исходные данные для расчета водопритоков
через совершенную завесу котлована по схеме «большого колодца»
| Наименование и размерность параметра | Характеристика параметра | Значения детерминированных параметров | Выборочные статистики | |||
| среднее | стандарт | асимметрия | эксцесс | |||
| Напор, м | Случайный | – | 20 | 4 | – | – |
| Глубина завесы, м | Случайный | – | 15 | 3 | – | – |
| Коэффициент пьезопроводности, м2/сут | Случайный | – | 4107 | 4106 | – | – |
| Коэффициент фильтрации, м/сут | Случайный | – | 10 | 4 | 1,5 | 4 |
| Коэффициент фильтрации в затампонированной зоне, м/сут | Случайный, варьируемый | – | 1,0 | 0,4 | 0,5 | 2 |
| – | 0,1 | 0,04 | 0,5 | 2 | ||
| – | 0,01 | 0,004 | 0,5 | 2 | ||
| Приведенный радиус , м | Стабильный | 50 | – | – | – | – |
| Время дренирования, сут | Стабильный | 10 | – | – | – | – |
| Допустимый приток, м3/сут | Стабильный | 30 | – | – | – | – |
| Примечание: Варьируемые значения коэффициентов фильтрации kт отвечают результатам тампонажа обычными цементными суспензиями с удельной поверхностью 3 м2/г, суспензиями на вибродомолотых цементах с удельной поверхностью 5 м2/г, суспензиями «Микродура» с удельной поверхностью 24 м2/г . |
Таблица 6
Результаты моделирования водопритоков в котлован
в зависимости от мощности тампонажной завесы
| Мощность завесы, м | Приток воды через завесу, м3/сут | |||||
| детермини-рованный расчет | вероятностный расчет | |||||
| среднее выборочное / риск | с риском 20 % | с риском 10 % | с риском 5 % | риск затопления котлована | ||
| Коэффициент фильтрации протампонированной зоны 1,0 м/сут | ||||||
| 3 | 119,3 | 107,3 / 0,356 | 155,4 | 186,9 | 246,5 | 0,978 |
| 9 | 103,9 | 90,1 / 0,378 | 124,6 | 156,6 | 205,9 | 0,970 |
| 15 | 93,0 | 79,5 / 0,400 | 106,2 | 136,5 | 187,3 | 0,970 |
| Коэффициент фильтрации протампонированной зоны 0,1 м/сут | ||||||
| 3 | 66,1 | 55,9 / 0,415 | 73,2 | 99,9 | 116,9 | 0,822 |
| 6 | 45,2 | 38,5 / 0,393 | 56,0 | 67,7 | 86,1 | 0,585 |
| 9 | 34,7 | 29,9 / 0,385 | 41,2 | 52,7 | 65,1 | 0,385 |
| 12 | 28,5 | 24,7 / 0,383 | 34,9 | 44,2 | 51,4 | 0,274 |
| 15 | 24,3 | 21,2 / 0,400 | 29,6 | 38,6 | 43,1 | 0,193 |
| Коэффициент фильтрации протампонированной зоны 0,01 м/сут | ||||||
| 3 | 12,1 | 10,8 / 0,400 | 15,1 | 19,8 | 22,1 | 0,148 |
| 6 | 6,5 | 5,9 / 0,430 | 8,4 | 10,9 | 12,1 | 0,000 |
| 9 | 4,5 | 4,1 / 0,422 | 5,9 | 7,6 | 8,7 | 0,000 |
| 12 | 3,5 | 3,2 / 0,422 | 4,6 | 5,9 | 6,7 | 0,000 |
| 15 | 2,9 | 2,6 / 0,415 | 3,8 | 4,7 | 5,9 | 0,000 |
Таблица 7
Данные для вероятностного расчета радиусов инъекции
вязко-пластичной жидкости по схеме бокового нагнетания
-
Обозначение параметров
Размерность
Характеристика параметра
Значения
постоянных
параметров
Закон
Распределения
Выборочные статистики
среднее
выборочное
стандарт
асимметрия
эксцесс
PR
МПа
Ver
–
N
1,6
0,12
–
–
h
м
Ver
–
N
15
1
–
–
P0
МПа
Ver
–
N
6,5
0,13
–
–
Kп
м2
Ver
–
GS
1,15710–12
1,73610–13
– 1,5
3,0
с
Нсм–2
Ver
–
N
0,022
0,002
–
–
0
Нм–2
Ver
–
N
0,46
0,1
–
–
Нм–3
Ver
–
N
13000
1000
–
–
Q
м3с–1
Ver
–
N
6,94410–4
2,89410–5
–
–
M
–
Ver
–
N
0,05
0,005
–
–
r0
М
const
0,05
–
–
–
–
–
Примечание. Ver, const – вероятностные и детерминированные параметры, соответственно, N – нормальное распределение, GS – распределение Грамма-Шарлье.
В табл. 8 приведены демонстрационные результаты моделирования радиусов инъекции, в табл. 9 – поинтервальные вероятности для массива радиусов инъекции вязко-пластичной жидкости в границах вариационного размаха от Rmin 0,3 м до Rmax 1,424 м, на рис. 4 – гистограмма и статистики распределения радиусов, на рис. 5 – связь между рисками и радиусами инъекции.
Предельное давление нагнетания – важнейший технологический параметр, определяющий эффективность инъекции грунтов в режимах пропитки, гидроразрыва, а также в зонах расположения инженерных конструкций, зданий и сооружений. Риск-анализ предельного давления нагнетания, выполняемый методом Монте-Карло, устраняет субъективность и неопределенность при принятии решения, создает предпосылки реализации принципа оптимальной экономической безопасности. В вероятностной постановке условие вычисления риска превышения предельного давления выражается неравенством Pпрд / P0< 1, здесь P0, Pпрд – рабочее и предельное давления нагнетания. Принцип оценки риска поясняется демонстрационными данными статистического моделирования, приведенными в табл. 10.
Таблица 8
Отсортированные радиусы инъекции, полученные методом Монте-Карло
| Радиус инъекции, м |
| 0,30 0,35 0,36 0,36 0,37 0,38 0,39 0,39 0,40 0,40 0,40 0,40 0,41 0,42 0,43 0,43 0,45 0,45 0,46 0,46 0,46 0,47 0,47 0,47 0,47 0,47 0,48 0,48 0,48 0,48 0,49 0,49 0,49 0,49 0,50 0,50 0,50 0,51 0,51 0,52 0,52 0,53 0,54 0,54 0,54 0,54 0,55 0,55 0,55 0,55 0,55 0,56 0,56 0,56 0,56 0,57 0,57 0,58 0,58 0,58 0,59 0,59 0,59 0,60 0,62 0,63 0,63 0,63 0,63 0,63 0,64 0,65 0,65 0,65 0,66 0,66 0,66 0,66 0,66 0,66 0,67 0,67 0,67 0,68 |
Окончание таблицы 8
| 0,68 0,68 0,68 0,68 0,68 0,68 0,69 0,69 0,69 0,69 0,70 0,70 0,72 0,73 0,74 0,74 0,75 0,77 0,77 0,77 0,77 0,78 0,78 0,78 0,80 0,81 0,81 0,81 0,83 0,86 0,86 0,87 0,87 0,89 0,91 0,91 0,92 0,93 0,93 0,94 0,96 0,97 1,01 1,06 1,07 1,14 1,16 1,22 1,39 1,42 |
Таблица 9
Поинтервальные вероятности для массива радиусов инъекции
| Интервал | Вероятность попадания в интервал | Интервал | Вероятность попадания в интервал | ||
| номер | границы, м | номер | границы, м | ||
| 1 | 0,300 0,352 | 0,007 | 11 | 0,860 0,916 | 0,045 |
| 2 | 0,352 0,409 | 0,082 | 12 | 0,916 0,973 | 0,045 |
| 3 | 0,409 0,465 | 0,067 | 13 | 0,973 1,092 | 0,007 |
| 4 | 0,465 0,522 | 0,149 | 14 | 1,092 1,086 | 0,015 |
| 5 | 0,522 0,578 | 0,127 | 15 | 1,086 1,142 | 0,007 |
| 6 | 0,578 0,634 | 0,082 | 16 | 1,142 1,198 | 0,007 |
| 7 | 0,634 0,691 | 0,172 | 17 | 1,198 1,255 | 0,007 |
| 8 | 0,691 0,747 | 0,067 | 18 | 1,255 1,311 | 0,000 |
| 9 | 0,747 0,804 | 0,052 | 19 | 1,311 1,368 | 0,000 |
| 10 | 0,804 0,860 | 0,045 | 20 | 1,368 1,424 | 0,015 |
 | |  |
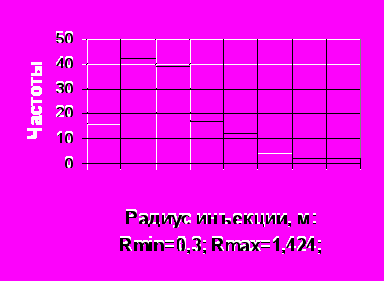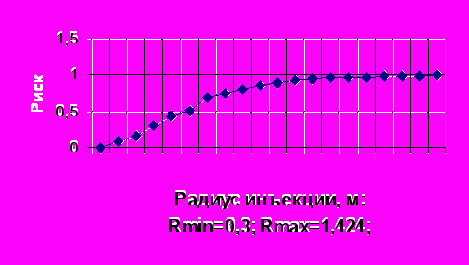| Рис. 4. Гистограмма распределения радиуса инъекции вязко-пластичной жидкости: Rср0,649; SR0,205; AR1,166; ER1,824 | Рис. 5. Связь между рисками и радиусами инъекции |
Таблица 10
Отсортированные показатели Pпрд /P0, полученные методом Монте-Карло
| Pпрд / P0 |
| 0,694 0,729 0,812 0,818 0,849 0,857 0,877 0,889 0,893 0,918 0,942 0,945 1,030 1,053 1,096 1,126 1,136 1,168 1,170 1,185 1,250 1,251 1,260 1,270 1,294 1,307 1,315 1,325 1,343 1,365 1,380 1,416 1,419 1,451 1,462 1,465 1,475 1,482 1,510 1,515 1,556 1,558 1,565 1,588 1,596 1,603 1,650 1,653 1,671 1,677 1,691 1,695 1,712 1,712 1,746 1,759 1,762 1,771 1,784 1,785 1,828 1,838 1,843 1,843 1,844 1,874 1,922 1,926 2,006 2,010 2,028 2,061 2,062 2,100 2,111 2,114 2,116 2,125 2,153 2,158 2,171 2,179 2,189 2,190 2,308 2,309 2,325 2,379 2,389 2,424 2,435 2,445 2,446 2,467 2,487 2,501 2,523 2,600 2,607 2,673 2,747 2,850 2,945 2,986 3,043 3,180 3,189 3,232 3,245 3,356 3,495 3,563 3,607 3,651 3,667 3,890 3,929 4,122 4,282 4,659 5,129 5,163 5,389 5,632 6,720 6,885 7,059 7,996 10,334 10,950 11,508 14,991 22,853 54,637 |
Уровень риска по фактору превышения предельного давления, согласно табл. 10 составляет 12 / 134 0,0896, надежность 0,9104.
Вероятностный анализ схем размещения тампонажных скважин в завесе является универсальным средством поиска рационального расположения скважин. Он позволяет найти разумный экономический компромисс между двумя альтернативами: обеспечение плотности завесы в результате смыкания полей инъекции, создаваемых вокруг каждой тампонажной скважины; исключение попадания вновь буримых скважин в ранее протампонированную область. На рис. 6 приведен пример расчетной схемы, а в табл. 11 данные вероятностного анализа расположения скважин в линейной тампонажной завесе.
Исследования, выполненные в главе 3, составили необходимую ранее отсутствовавшую базу для повышения качества формирования противофильтрационных завес. Вероятностный подход объясняет причины резкого несоответствия, наблюдаемого на практике между расчетными показателями и фактическими результатами, в частности, разброс результатов тампонирования в пределах завесы, возможность возникновения «окон», утечек тампонажных жидкостей, перерасхода ресурсов. В результате выполненных исследований установлены основные факторы риска и разработаны имитационные методики количественной оценки факторов, сопровождающих строительство и эксплуатацию тампонажных завес городских подземных сооружений: превышение нормируемого остаточного притока воды, подтопление и затопление строящегося или эксплуатируемого объекта; перерасход тампонажных материалов; завышенный объем буровых работ; разрушение или повреждение обделок подземных сооружений или их элементов; деформации вмещающего массива, зданий и сооружений, расположенных непосредственно в зоне производства тампонажной завесы или вблизи ее; увеличение сроков выполнения тампонажных работ.
-
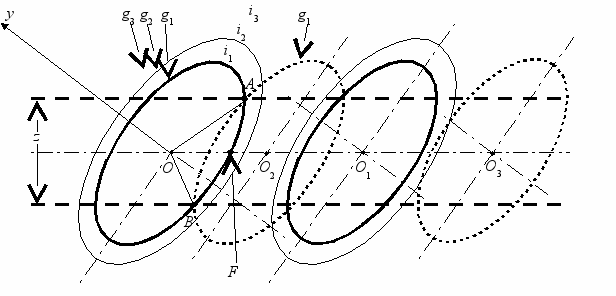
Рис. 6. Схема к вероятностному анализу расположения
скважин однорядной линейной завесы в анизотропных грунтах:
z – проектная мощность завесы; O, O1, O2, … – тампонажные скважины; g1, g2, g3, … – риски инъекции; i1, i2, i3, … – интервальные риски
Таблица 11
Риски инъекции и риски попадания вновь буримых скважин в эллипс инъекции
-
Интервал
Риск
инъекции
Параметры
эллипса
инъекции, м
Расстояние от скважины до
границы эллипса
инъекции
по оси ряда, м
Расстояние между
скважинами первой
и второй очередей,
м
Риск попадания скважины в поле инъекции
a
B
1
2
3
…
0,150
0,361
0,451
…
0,955
1,543
2,132
…
0,478
0,772
1,066
…
0,530
0,856
1,182
…
1,008
1,629
2,250
…
0,090
0,098
0,045
…
4. Оптимизация технологических параметров тампонажных завес
Составляющими современной теории риска, помимо изучения факторов риска и методов оценки риска, являются: определение цены риска, нормирование риска, управление риском. Полная цена риска для тампонажных завес определяется исходя из совокупности частной цены рисков по каждому из установленных факторов риска. Частная цена рисков равна произведению уровня риска на потенциальный ущерб, характеризующий непроизводительные затраты исполнителя работ или убытки заказчика при эксплуатации построенного подземного объекта (с учетом принципа «финансового запаса»).
Среди рассмотренной совокупности факторов риска наибольшие затруднения возникают при определении цены риска превышения нормативного или недопустимого водопритоков. Остаточный или недопустимый притоки воды сопровождаются ущербами в результате непроизводительных затрат на откачку, агрессивных воздействий воды на конструкции подземного сооружения, ухудшения санитарного состояния внутренних помещений. Суммарное количество поступающей воды устанавливается по результатам вероятностного анализа водопритоков через завесу с учетом формы завесы, расположения тампонажных скважин в завесе, порядка и способов тампонирования. Методика определения цены этого риска включает: 1 – формирование методом Монте-Карло шкалы границ (радиусов инъекции) и соответствующих им интервалов и поинтервальных рисков; 2 – вариантное определение числа тампонажных скважин; 3 – определение суммарной длины «окон» (незатампонированных участков завесы) в соответствии с числом интервалов и границами интервалов; 4 – генерацию массива вероятных водопритоков через «окна»; 5 – генерацию массива вероятных водопритоков через тело завесы; 6 – суммирование водопритоков (пример в табл. 12); 7 – фиксацию составляющих ущербов от водопритока; 8 – вычисление цены риска с учетом фактора времени, например, по формуле
tt n
Собв. ((Qсум – Qнорм) Уобв i)t (1 E)–t,
t1 i=1
где Собв – цена риска;. Уобв i – составляющие ущерба, i 1, n; Qнорм – нормируемый остаточный водоприток; t – время строительства объекта с момента завершения завесы; E – норма, учитываемая при дисконтировании затрат и доходов инвестора или строительной организации.
Таблица 12