Метод деления отрезка пополам

Вид материала

Документы

Подобный материал:

• Расшифровка : Наука в целом (информационные технологии 004), 79.71kb.
• Это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок, 53.74kb.
• А. В. Ремнев Омский государственный университет, 489.1kb.
• Курс 3 семестр Решения нелинейных уравнений методом половинного деления. Блок-схема, 25.7kb.
• Правила определения понятий. Логическая операция деления понятий. Правила деления понятий., 127.01kb.
• Способы деления эукариотических клеток: митоз, мейоз, амитоз, 51.33kb.
• Лекция №4 Тема: «Авария на чаэс», 173.57kb.
• Темы курсовых работ по курсу «Программирование» для студентов группы биб-11-1 (2011-2012, 85.51kb.
• Упростите: -, 10.56kb.
• Она засмеялась лёгким непринуждённым смехом. Хер тотчас же подхватил его и согнулся, 159.72kb.

Метод деления отрезка пополам

Это один из простейших методов нахождения корней нелинейного уравнения.

Требуется найти корень уравнения F(x)=0 с точностью . Пусть удалось отделить корень на отрезке [a₀,b₀]. В качестве начального приближения к корню выбирают середину отрезка

,

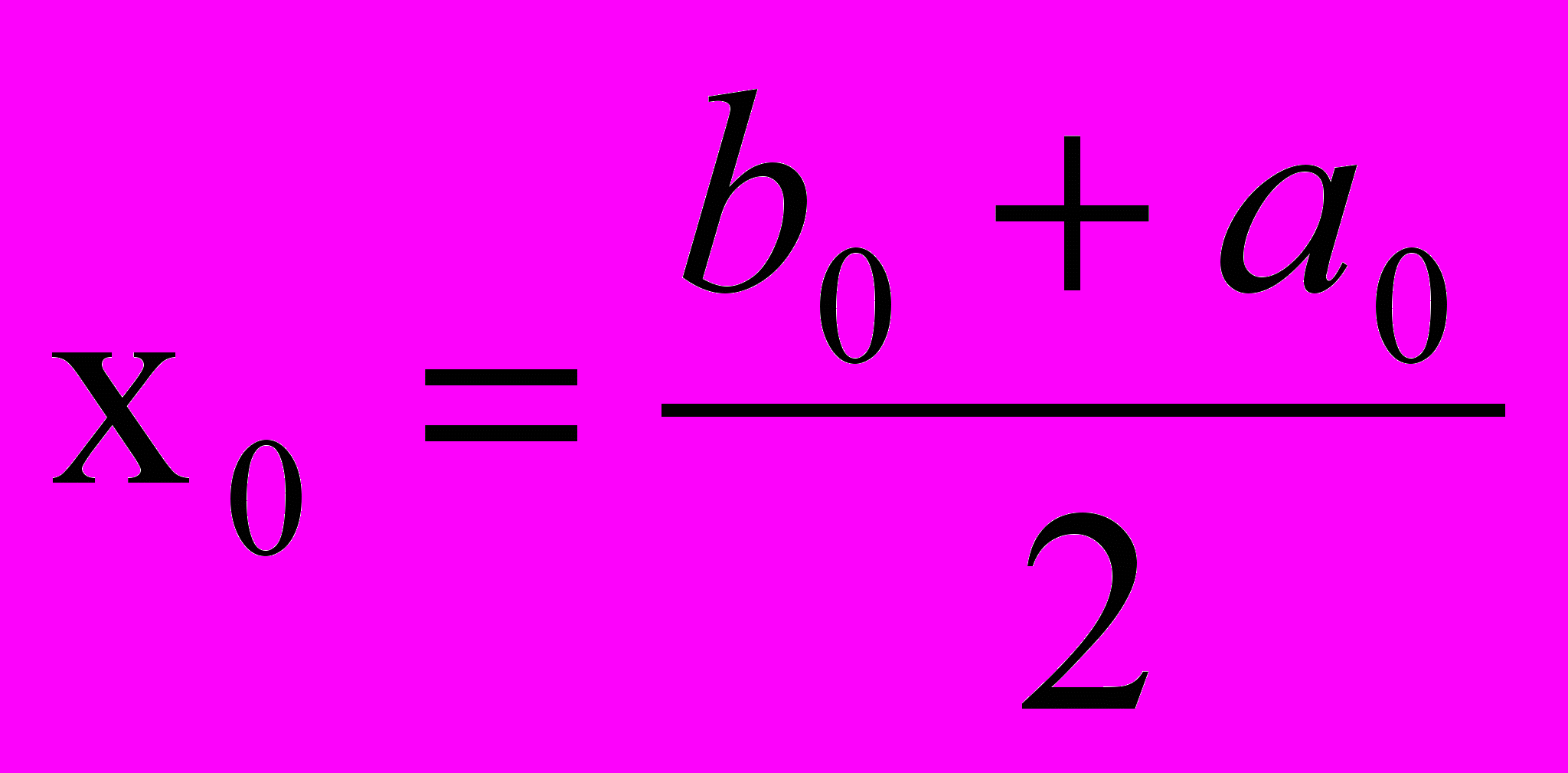затем определяют, слева или справа от середины отрезка функция меняет знак (т.е. слева или справа от середины отрезка находится точный корень), и в качестве следующего приближения берут середину того отрезка, где происходит перемена знака

[a_i+1,b_i+1]=[a_i,x_i], если F(a)*F(x_i)<0;

[a_i+1,b_i+1]=[x_i,b_i], если F(b)*F(x_i)<0;

где i=0, 1 ….

Получают последовательность вложенных отрезков[a_i,b_i], стягивающихся к точному корню уравнения, причем каждый следующий отрезок в два раза короче предыдущего. Процесс заканчивают, когда длина отрезка меньше , т.е. погрешностью i-го приближения к корню является в данном методе длина отрезка [a_i,b_i]

r_i = b_i-a_i .

Метод деления отрезка пополам сходится всегда, но сходится очень медленно. Большое количество вычислений нужно проделать, чтобы добиться высокой точности. Он является самым простым, надежным, но неэффективным методом.