А. Н. Фоменко, канд техн наук

Вид материала

Содержание

V — стоимость (текущая) потока доходов; I
Таблица 1. Местоположение точки «приписки» годового дохода
S — сумма членов бесконечной убывающей геометрической прогрессии; b
Yр — реальная ставка доходности; t
Таблица 2. Погрешности расчетов при использовании номинальных и реальных ставок доходности
Варианты исходных данных
Погрешность (различия) между результатами расчета стоимости актива по методу ПК и методу ДДП
Стоимость реверсии по Y

Подобный материал:

А.Н. Фоменко, канд. техн. наук,
генеральный директор ООО «АНФ-ОЦЕНКА»,
член Экспертного совета РОО
Московская обл.

О ПРАВИЛАХ ДИСКОНТИРОВАНИЯ ПРИ ПРАКТИЧЕСКОЙ ОЦЕНКЕ

Ключевые слова: метод дисконтированных денежных потоков, метод прямой капитализации, стоимость реверсии, ставка доходности, метод Инвуда, прогнозный и постпрогнозный периоды.

Аннотация

Среди практикующих оценщиков существуют различные мнения по поводу правил дисконтирования стоимости реверсии при смещении годовых доходов в середину периода и правил применения метода прямой капитализации. Логически и математически обосновано, что в этом случае стоимость реверсии также должна быть смещена на середину последнего года прогнозного периода. Сформулированы правила, обеспечивающие совпадение результатов расчетов методом прямой капитализации и методом дисконтированных денежных потоков при различной структуре потока доходов в постпрогнозном периоде.

На первый взгляд, правила дисконтирования денежных потоков и вопросы применения метода прямой капитализации давно описаны в литературе, поэтому говорить, казалось бы, не о чем. Однако опыт общения в среде практикующих оценщиков показывает, что все не столь однозначно.

Дело в том, что в классическом методе дисконтированных денежных потоков (ДДП) предполагается, что потоки доходов поступают в конце периода и дисконтируются на целочисленные периоды (обычно в годовом исчислении). В какой-то степени такое правило дисконтирования объясняется тем, что во времена разработки метода ДДП не было совершенных счетных приборов, способных без затруднений возвести число в любую дробную степень. Однако даже тогда допускалась возможность поступления доходов с фиксированной периодичностью в течение года. Для того чтобы обойти необходимость возведения числа в дробную степень, был «придуман» метод перехода от дробных степеней к целочисленным при дисконтировании. Для периода в один год такая зависимость имеет вид

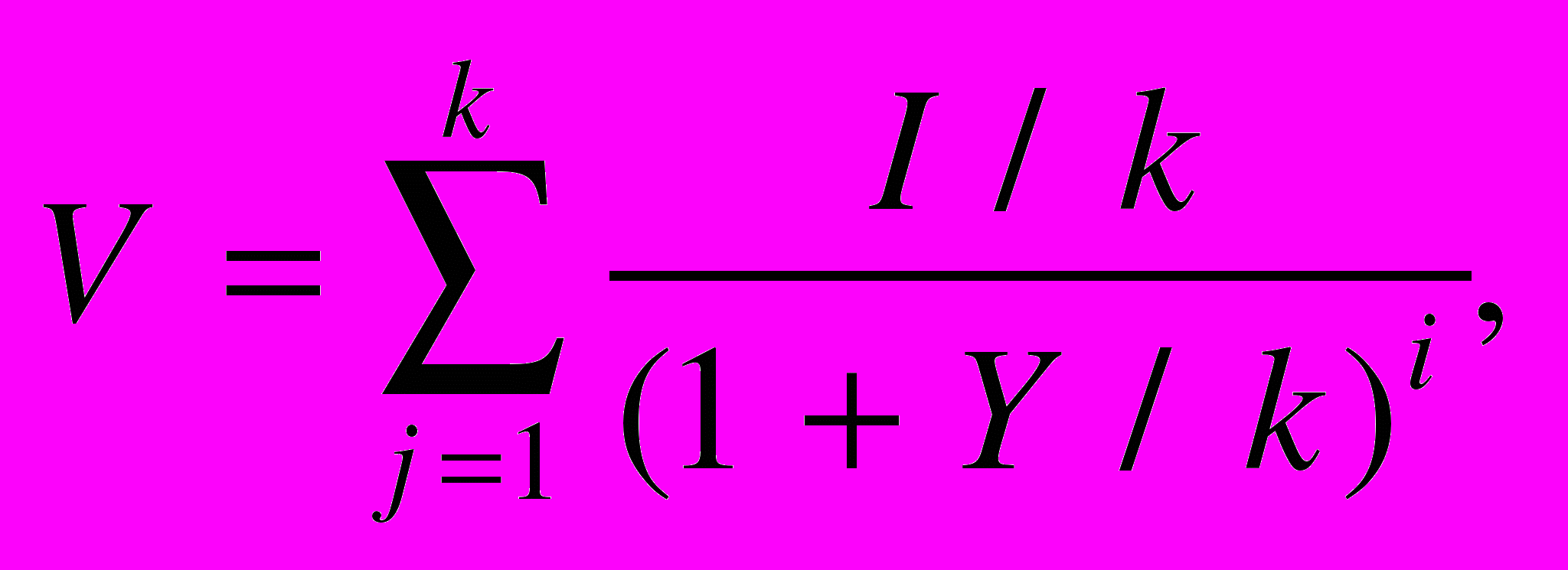(1)

где

V — стоимость (текущая) потока доходов;

I — годовой чистый доход;

Y — ставка дисконтирования (годовая ставка доходности);

k — количество платежей (элементов денежного потока) в течение года;

j — номер текущего платежа.

Однако, если подходить строго, то нужно учитывать, что метод ДДП предусматривает дисконтирование каждого элемента денежного потока на момент его поступления. Поэтому «правильная» формула для дисконтирования в рассматриваемом случае имеет следующий вид:

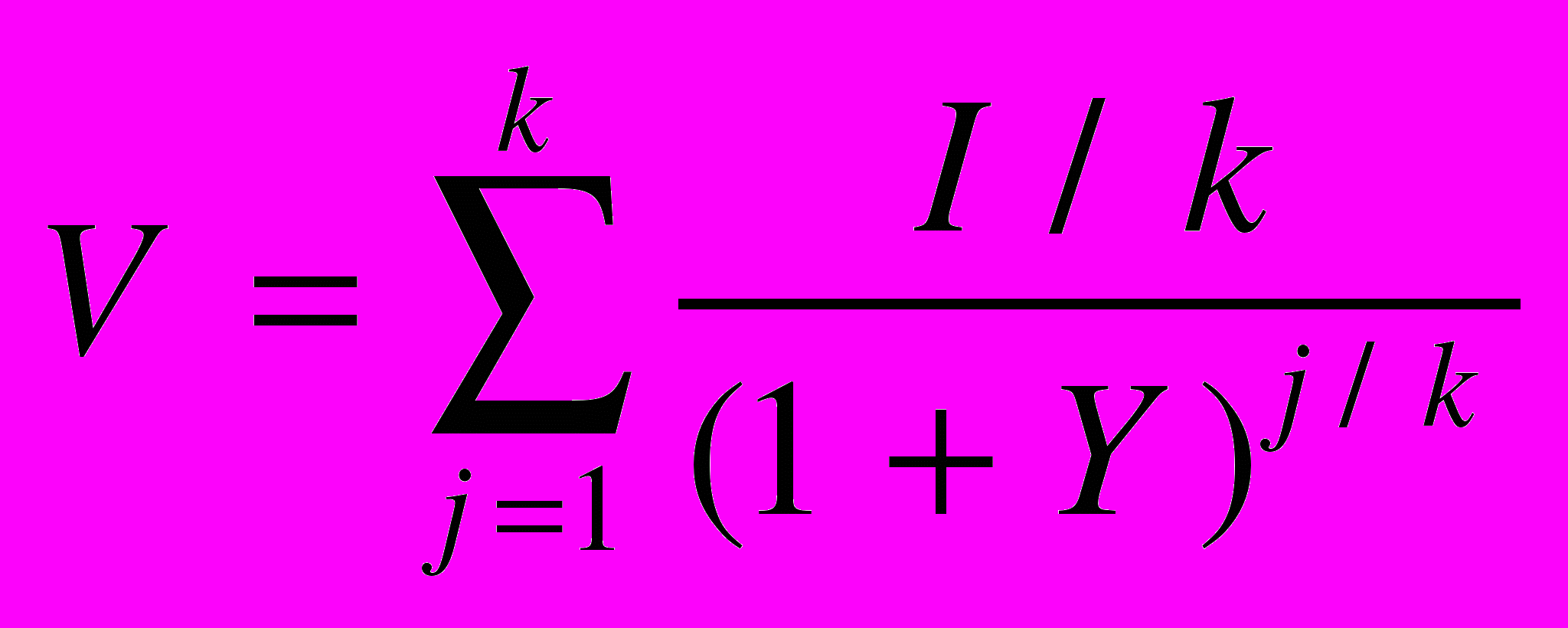(2)

Попробуем сравнить результаты расчета, например, при ежеквартальном поступлении доходов, которые схематично представлены на рис. 1, а (весь период — 1 год). При суммарном годовом потоке доходов, равном единице, и ставке дисконтирования 15 % расчетная величина согласно зависимости (1) составит 0,913, а согласно зависимости (2) — 0,917.

Поскольку при практической оценке количество годовых периодов в прогнозном периоде обычно достигает пяти, то дисконтировать каждый квартальный или месячный доход неудобно. Еще неудобнее описывать результаты такого расчета в отчете об оценке, поскольку таблица с результатами становится слишком громоздкой. Поэтому оценщики обычно оперируют годовыми доходами. В связи с этим возникает вопрос: к какому моменту времени приписать годовой доход? Если приписать его к концу года, как показано на рис. 1, б, то при приведенных выше исходных данных получим, что стоимость дисконтированного потока равна 0,870. То есть стоимость существенно занижается по сравнению со стоимостью, полученной по «правильной» формуле. В качестве альтернативы можно приписать годовой доход к середине года (0,5 года — рис. 1, в). В этом случае стоимость дисконтированного потока равна 0,933. Отличие от результата, полученного по «правильной» формуле, будет меньше. Поэтому подавляющее большинство практикующих оценщиков дисконтирует потоки, элементы которого приписаны к середине года (или, как говорят, дисконтирование осуществляется «на середину периода»). В этом случае расчетная зависимость для периода в 1 год принимает вид

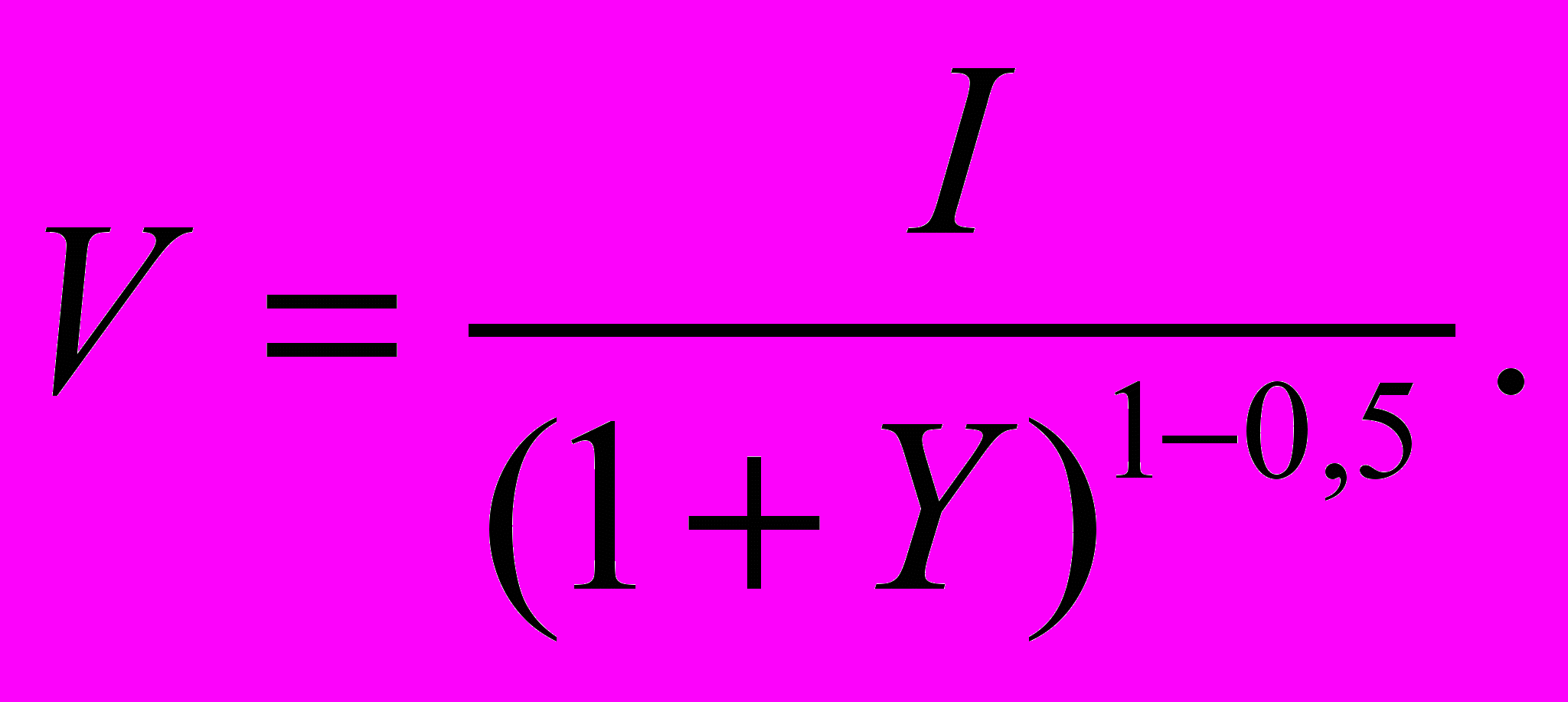
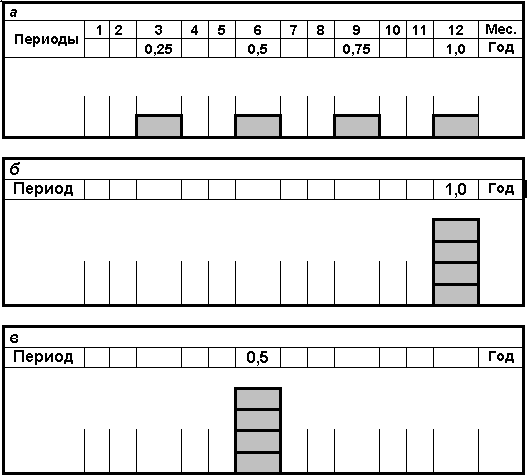
Рис. 1

При желании можно определить точное местоположение «приписки» годового дохода
(1 – а), обеспечивающее совпадение с результатом «правильной» формулы при различной периодичности получения доходов (табл. 1). Однако, учитывая относительно небольшую погрешность расчетов при периодичности поступления доходов раз в месяц или раз в квартал, на практике принято использовать дисконтирование «на середину периода» (0,5 года).

Таблица 1. Местоположение точки «приписки» годового дохода

Количество периодов поступления доходов в течение года j	365	12	4	1
Расчетное значение положения «точки приписки» 1 – a	0,4945	0,5348	0,6185	1,0000
Значение сдвига «точки приписки» a	0,5055	0,4652	0,3815	0,0000
Погрешность при дисконтировании «на конец периода», %	–8,7	–8,0	–6,5	0,0
Погрешность при дисконтировании «на середину периода», %	–0,1	0,6	1,9	7,9

Отметим, что банки продолжают придерживаться формулы (1). Видимо, это объясняется простотой расчета и возможностью дополнительно извлечь небольшой сверхдоход. Например, при приведенной выше ставке и ежеквартальных выплатах банк, выдав кредит в размере 913 д. е., получает годовое возмещение в размере 1000 д. е., которое соответствует кредиту в 917 д. е.

Вместе с тем, перейдя в массовом масштабе в методе ДДП от дисконтирования «на конец периода» к дисконтированию «на середину периода», оценщики столкнулись с неопределенностью: на какой период необходимо дисконтировать стоимость реверсии (стоимость потока доходов постпрогнозного периода)?

Классический вариант дисконтирования стоимости реверсии при поступлении доходов в конце периода схематично показан на рис. 2, а (5 лет прогнозного периода, начиная с 6-го года — постпрогнозный период). Альтернативные варианты дисконтирования стоимости реверсии при поступлении доходов в середине года показаны на рис. 2, б, в. Расчетные зависимости для каждой из приведенных схем имеют следующий вид:

схема 2, а:

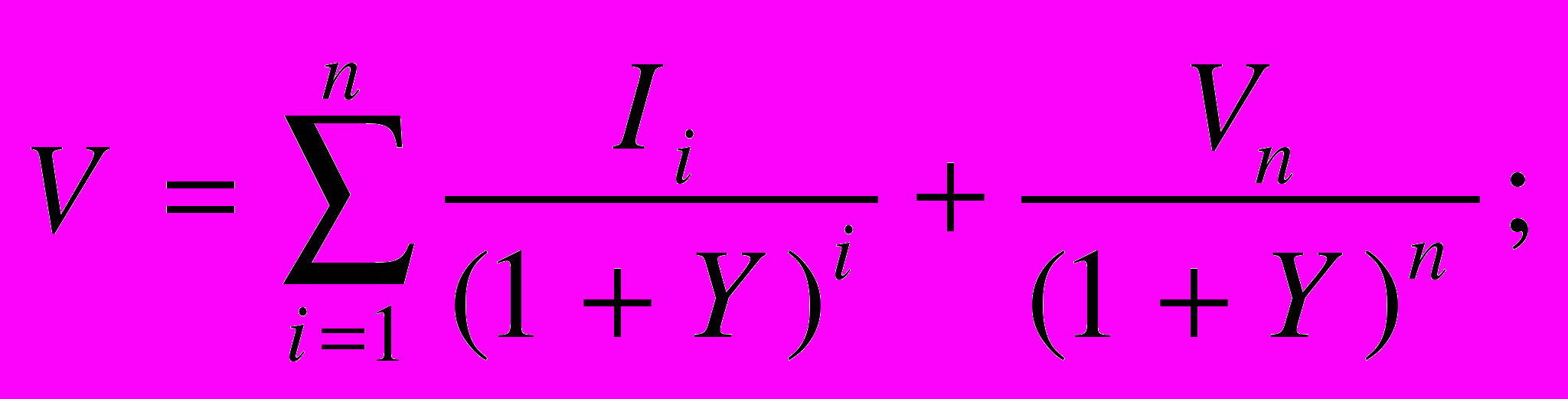
схема 2, б:

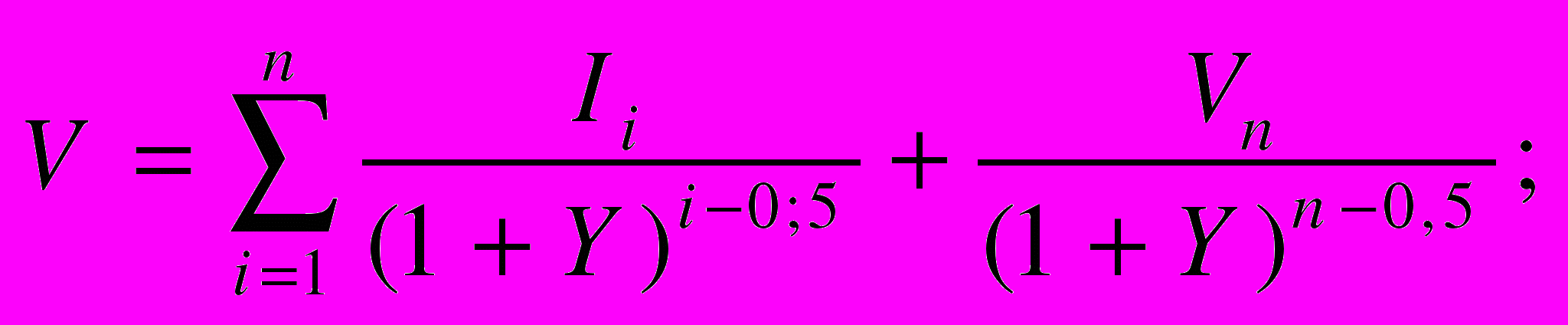
схема 2, в:

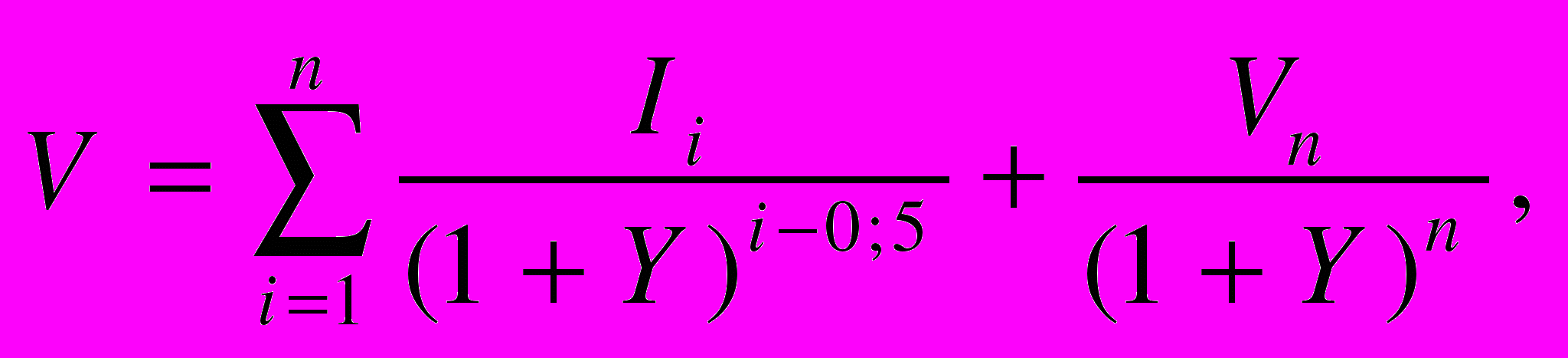
где

V_n — стоимость реверсии;

i – порядковый номер года прогнозного периода;

n — продолжительность прогнозного периода.

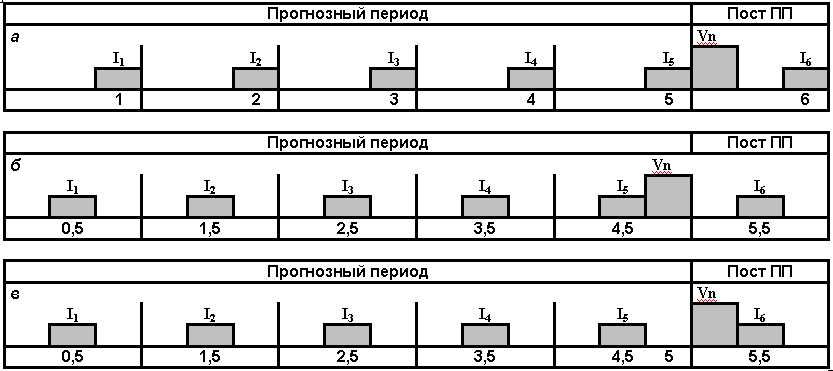
Рис. 2

Правило дисконтирования, показанное на рис. 2, в, приводится в ряде источников информации (например, [1, 2] и др.) и достаточно распространено среди практикующих оценщиков. Оно основано на логическом умозаключении, которое сводится примерно к следующему. Мы передвинули годовые доходы на середину года только для уменьшения погрешности расчетов, но продавать объект по стоимости реверсии мы по-прежнему собираемся по окончании прогнозного периода, который заканчивается через 5 лет. Поэтому и дисконтировать стоимость реверсии мы должны на начало 6-го года (конец 5-го года). То есть сдвиг доходов «на середину периода» не влияет на правило дисконтирования стоимости реверсии (иными словами, период ее дисконтирования всегда является фиксированным).

Попробуем обосновать необходимость применения схемы, изображенной на рис. 2, б. При этом к логическим умозаключениям вернемся позже, а пока рассмотрим «математику» — прежде всего потому, что метод ДДП представляет собой всего лишь математическую модель, описывающую реальные процессы инвестирования капитала и его возврат в виде периодического во времени потока доходов с учетом требуемой нормы отдачи (ставки доходности).

Для начала рассмотрим бесконечный поток доходов в постпрогнозном периоде, что характерно для неизнашиваемых (условно неизнашиваемых) активов, например, земли или бизнеса. Обычно принимают, что эти доходы в общем случае изменяются с постоянным темпом (роста или снижения). При таком изменении дисконтированную сумму доходов постпрогнозного периода на момент получения дохода 1-го года этого периода, можно выразить в виде суммы бесконечной убывающей геометрической прогрессии.

Напомним формулы геометрической прогрессии:

;

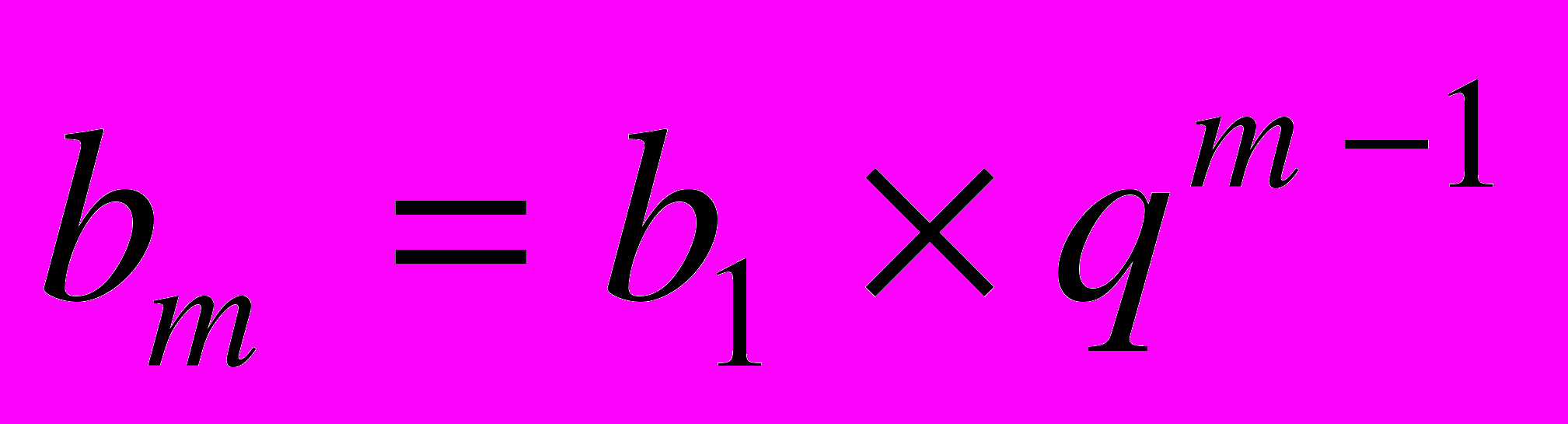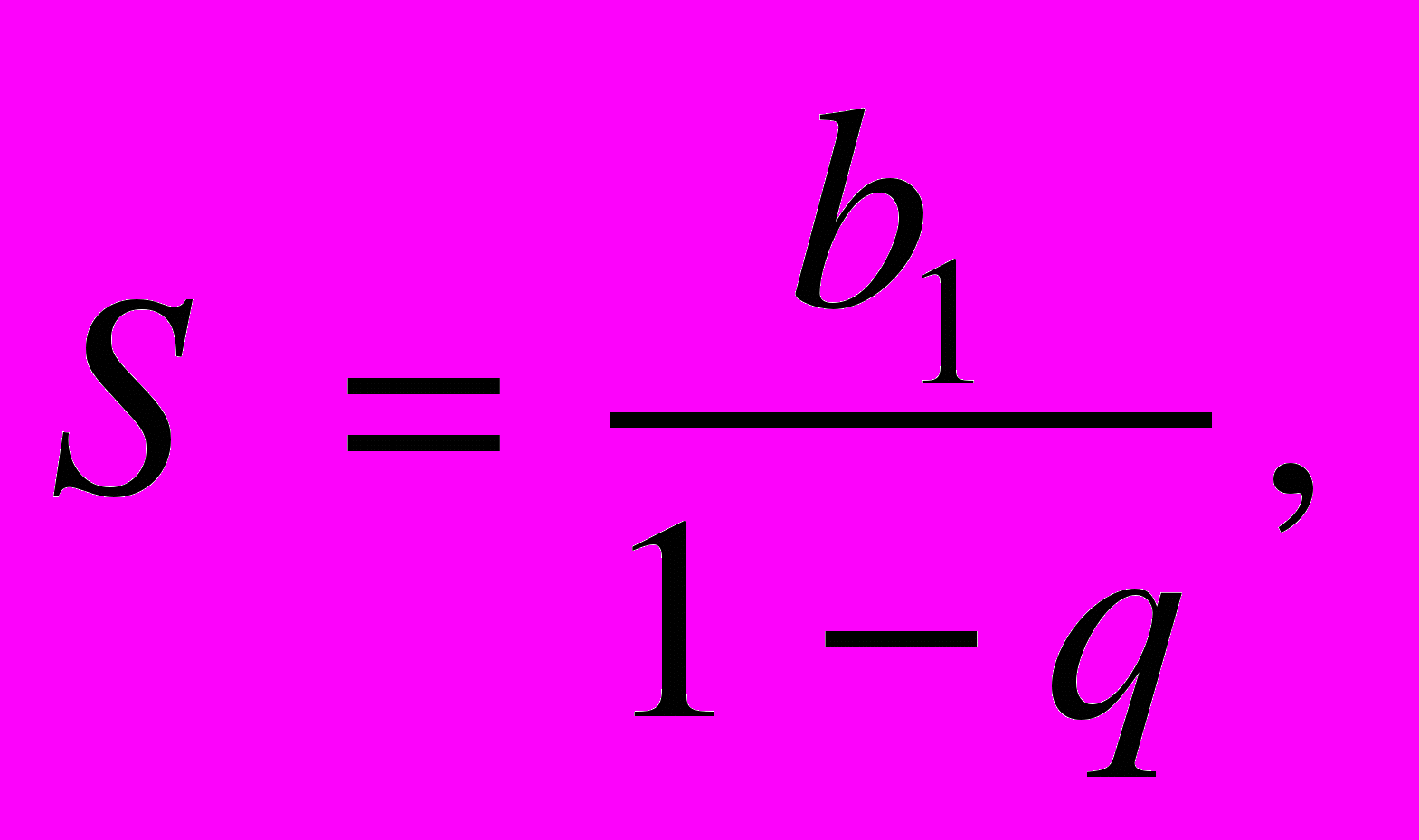(3)

где

S — сумма членов бесконечной убывающей геометрической прогрессии;

b₁ — первый член геометрической прогрессии;

b_m — любой m-й член геометрической прогрессии;

q — знаменатель геометрической прогрессии.

Для случая постпрогнозного периода имеем следующие элементы прогрессии:

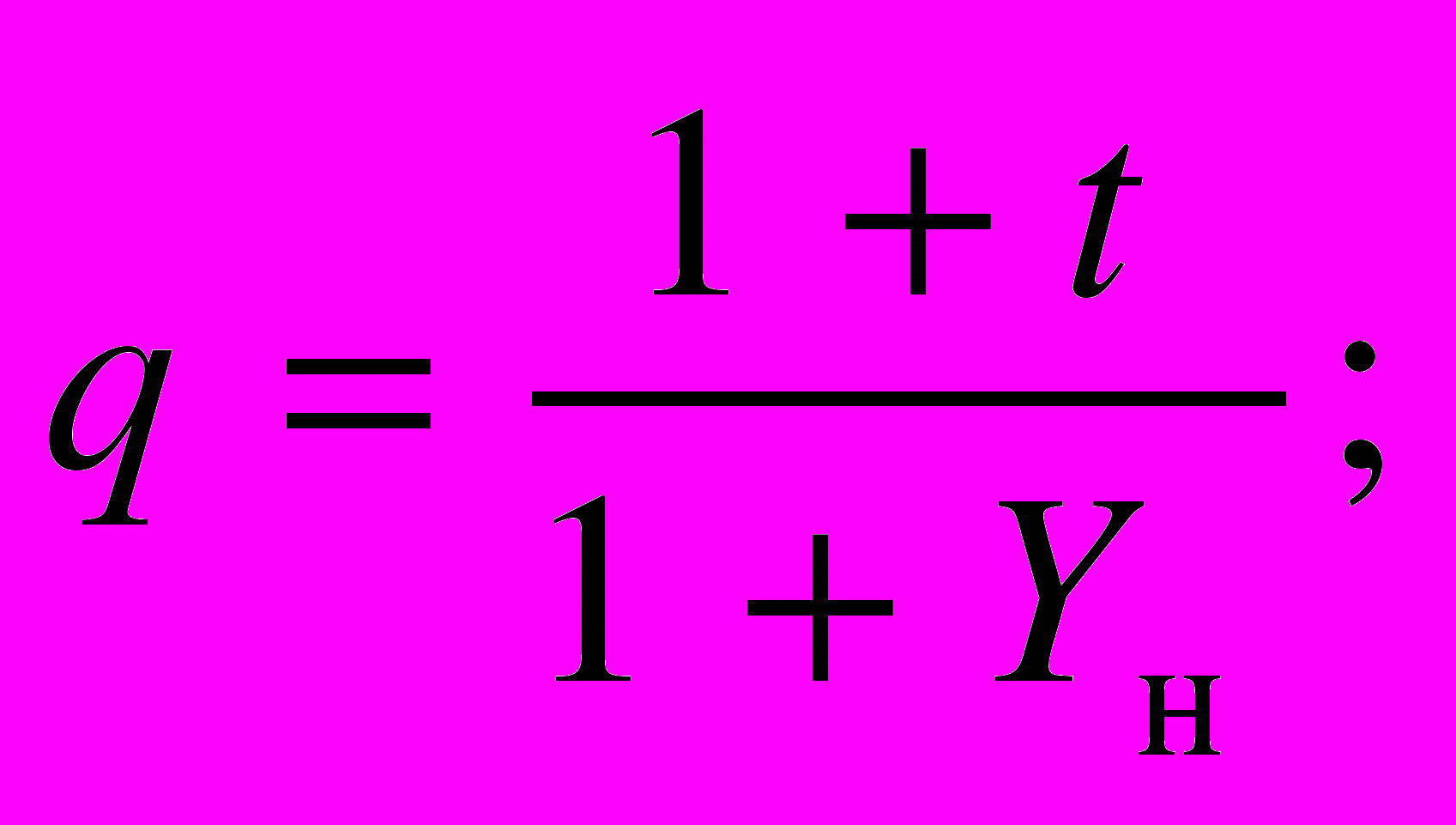
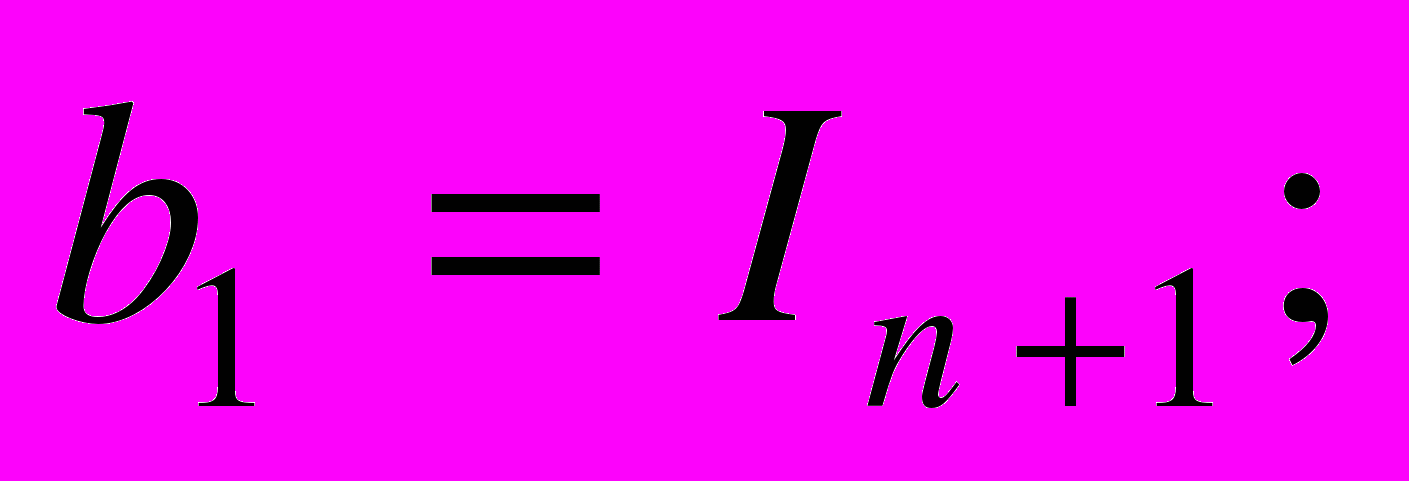
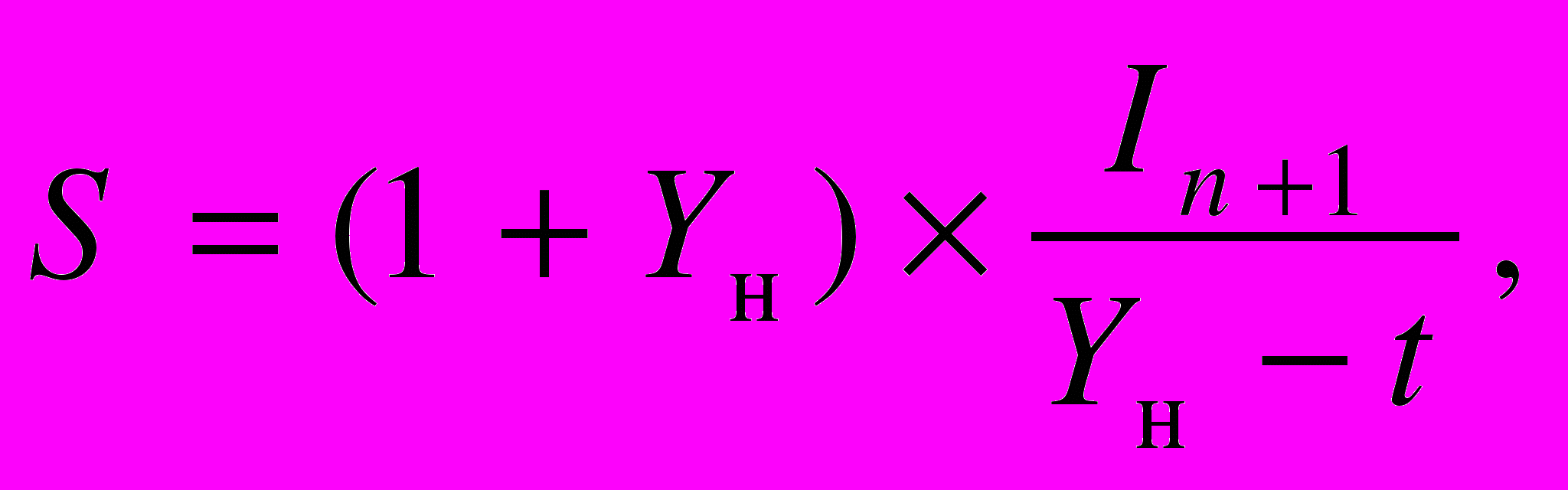
где

t — темп изменения (роста или снижения) величины годовых доходов в постпрогнозном периоде;

Y_н — номинальная ставка доходности.

Вместе с тем стоимость реверсии при бесконечном потоке доходов, как известно, выражается формулой Гордона. Подставляя в эту формулу значения полученной выше суммы прогрессии, получаем:

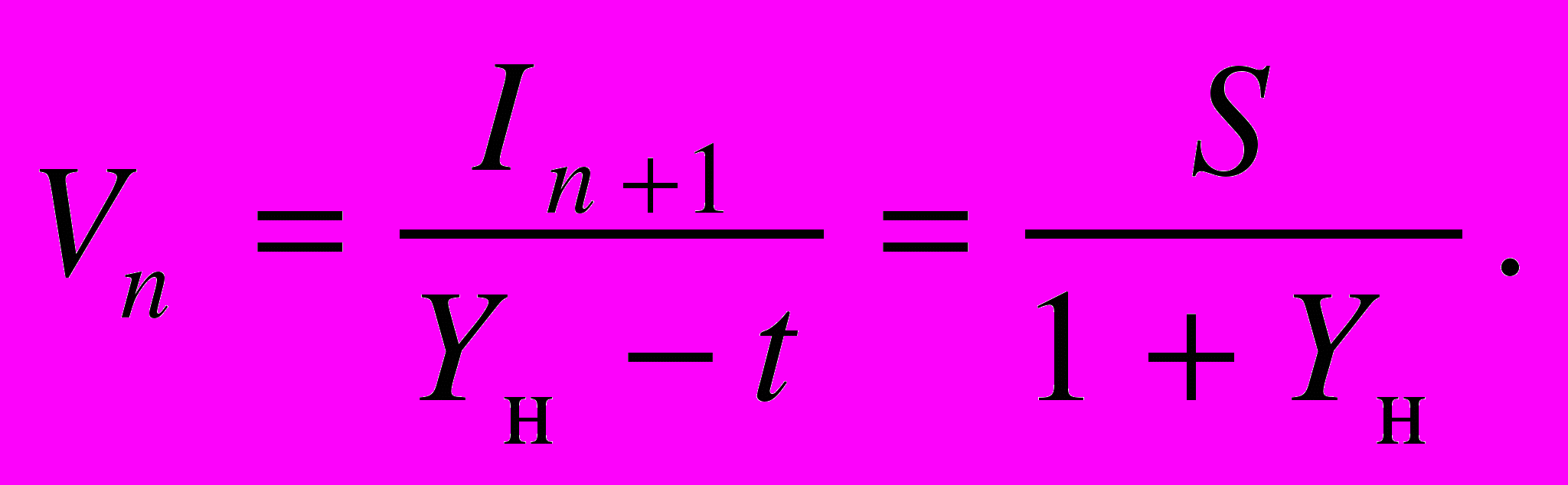(4)

Деление суммы прогрессии на (1 + Y_н) соответствует дисконтированию на 1 год назад относительно местоположения дохода 1-го года постпрогнозного периода. Следовательно, в случае дисконтирования «на середину периода» стоимость реверсии должна дисконтироваться на середину последнего года прогнозного периода (см. схему на рис. 2, б).

С учетом формулы Фишера, устанавливающей связь между номинальными и реальными ставками доходности

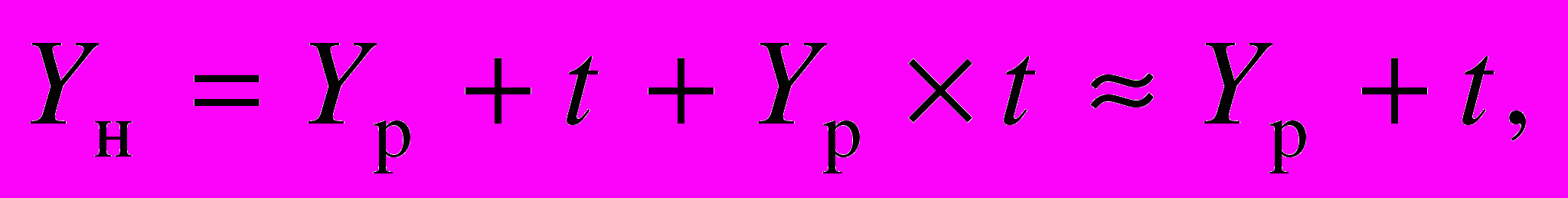(5)

можно записать

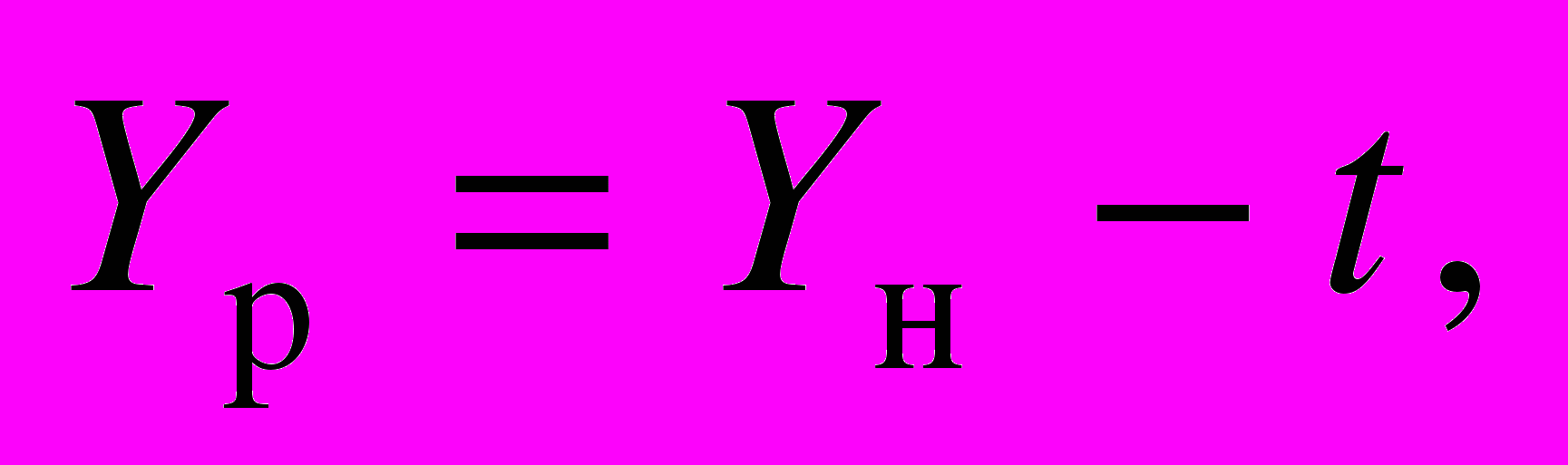
где

Y_р — реальная ставка доходности;

t — инфляция (темп роста стоимости) актива.

Следовательно, величина (Y_н – t) в формуле Гордона (4) по своей сути соответствует реальной ставке доходности, поскольку при постоянной ставке доходности темпы роста стоимости актива и темпы роста величины годовых доходов совпадают.

Отметим, что долгосрочный темп роста величины доходов не может быть равен или превышать значение номинальной ставки дисконтирования (доходности), поскольку в этом случае бесконечная убывающая прогрессия превращается в бесконечную возрастающую. Сумма такой прогрессии равна бесконечности (формула (3) неприменима). Такой же результат даст и метод ДДП. Следовательно, возможны два альтернативных предположения.

Первое — вывод о способности актива генерировать бесконечный поток доходов с назначенным долгосрочным темпом роста их величины, превышающим ставку доходности, предположительно неверен. Можно допустить, что в будущем предполагаются неучтенные периодические затраты на возобновление утраченных свойств (модернизацию) актива, что снижает реальный долгосрочный темп роста величины доходов.

Второе — в случае превышения долгосрочным темпом роста величины доходов значения номинальной ставки доходности следует предположить, что ставка доходности рассчитана неверно. Что бы убедиться в этом, необходимо провести исследование рынка объекта оценки, например, воспользоваться методом экстракции рынка.

Обратим внимание на то, что стоимость реверсии фактически определяется путем капитализации дохода 1-го года постпрогнозного периода, но при этом она соответствует моменту времени на один период назад. Если провести аналогию между процедурой расчета стоимости реверсии (при дисконтировании «на конец периода») и методом прямой капитализации (ПК), то в последнем случае дата оценки соответствует последнему году прогнозного периода, а капитализируемый доход — доходу следующего года (первому году постпрогнозного периода — прогнозное значение). Если доходы подвержены изменению с постоянным темпом (росту или снижению), то капитализируемый доход обязательно должен определяться с учетом этого темпа относительно величины текущего дохода (на дату оценки). В этом случае результаты расчетов методом ПК и методом ДДП совпадут.

В связи с этим хочется обратить внимание на распространенное среди практикующих оценщиков мнение при применении метода ПК, состоящее в том, что даже при наличии долгосрочных темпов изменения величины доходов необходимо капитализировать текущий доход (без учета темпа изменения его величины). Это мнение формируется на основе логического рассуждения о том, что при сдаче в аренду, например, земельного участка с возможностью роста ставки аренды по договору капитализируемый доход (за 1-й год) будет соответствовать текущей ставке аренды (на дату заключения договора аренды — дату оценки), поскольку ее увеличение возможно лишь через год. То есть в этом случае невольно предполагается, что эффективная величина текущего дохода (на дату оценки) равна реальной величине текущего дохода, уменьшенной (увеличенной) на величину годового прироста (снижения) в соответствии с долгосрочным темпом изменения, как бы соответствует величине дохода прошлого года. Поэтому корректность такого рассуждения представляется спорной. Однако в любом случае для обеспечения совпадения результатов расчетов методом ПК и методом ДДП необходимо капитализировать доход, который мы приписываем первому году в методе ДДП.

Для обеспечения совпадения результатов расчетов методом ПК и методом ДДП (при дисконтировании «на середину периода») капитализируемую прогнозную величину дохода для метода ПК необходимо дополнительно скорректировать. Величину корректировки можно определить из следующих соображений:

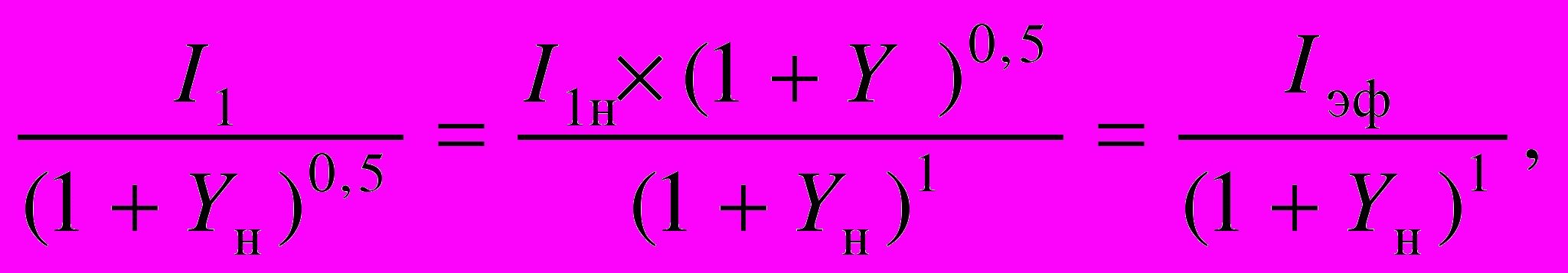
отсюда

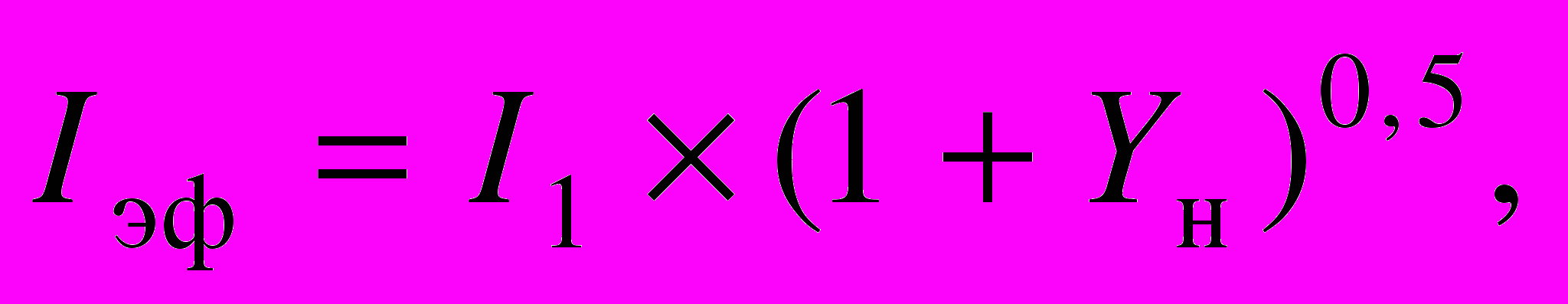
где

I₁ — капитализируемая прогнозная величина дохода, соответствующая величине дохода первого года в методе ДДП (равна текущей величине дохода на дату оценки, измененной в соответствии с темпом изменения за один год);

I_эф — эффективная величина капитализируемого (прогнозного значения) дохода.

Такая корректировка обеспечивает точное совпадение результатов расчетов методом ПК и методом ДДП (при дисконтировании «на середину периода»).

Далее рассмотрим постпрогнозный период с постоянным по величине, но ограниченным во времени потоком доходов (изнашиваемый актив). При этом сумму дисконтированного потока доходов в период с 1-го года постпрогнозного периода до года окончания срока жизни актива выразим в виде разности между суммой дисконтированного потока доходов в период с 1-го года постпрогнозного периода до бесконечности и суммой дисконтированного потока в период с 1-го года после года окончания срока жизни актива до бесконечности.

Поскольку для рассматриваемого случая

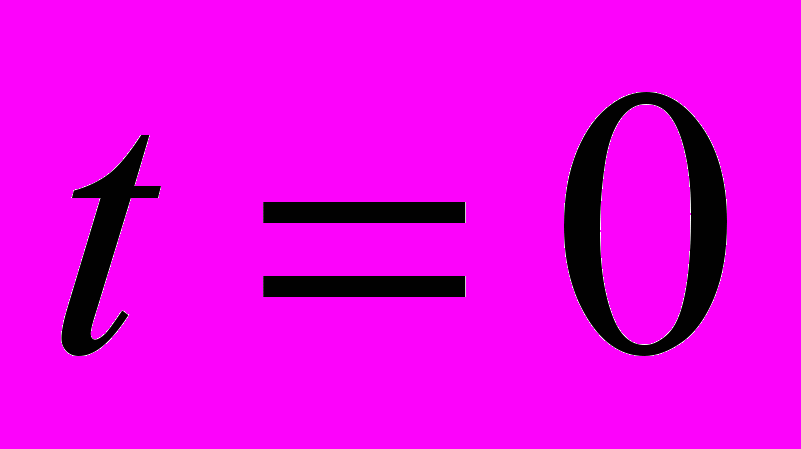, то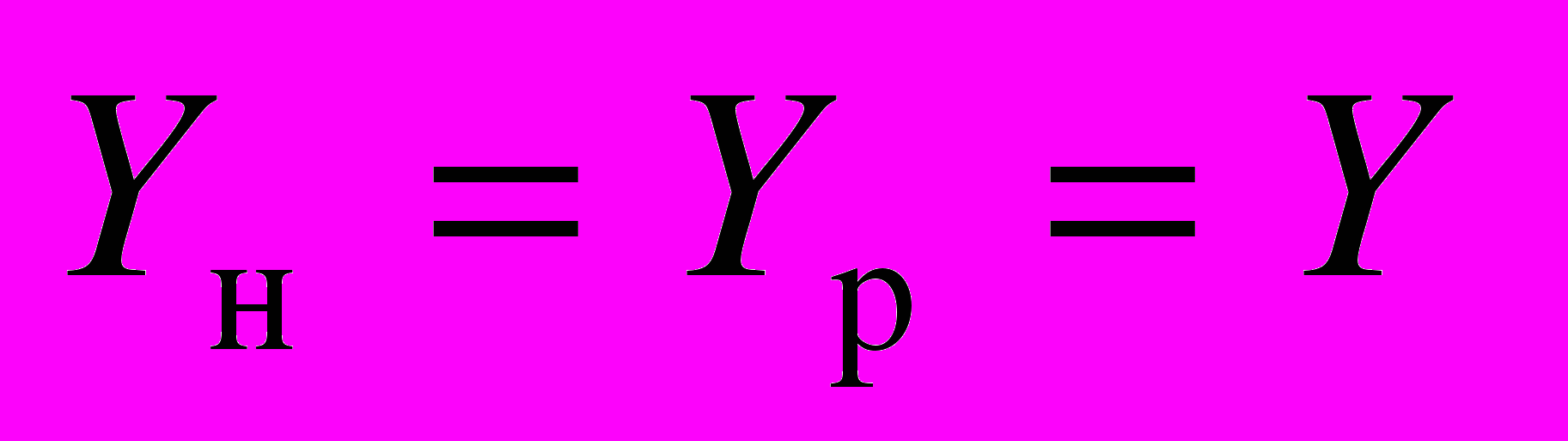

. Сумма дисконтированного потока доходов на момент (n + 1) в период с 1-го года постпрогнозного периода до бесконечности составляет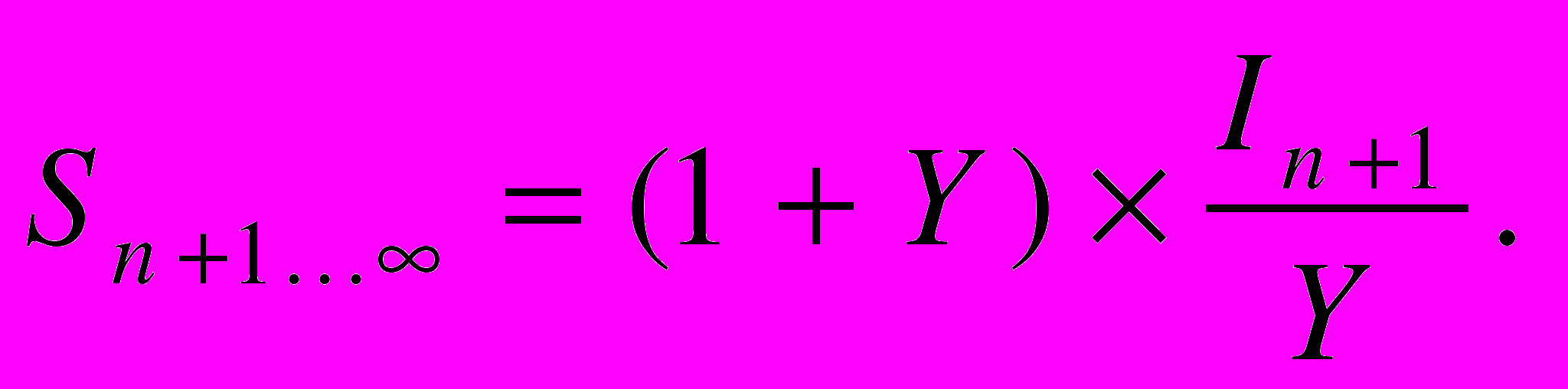

Сумма дисконтированного потока на момент (n + m + 1) в период с 1-го года после года окончания срока жизни актива до бесконечности равна

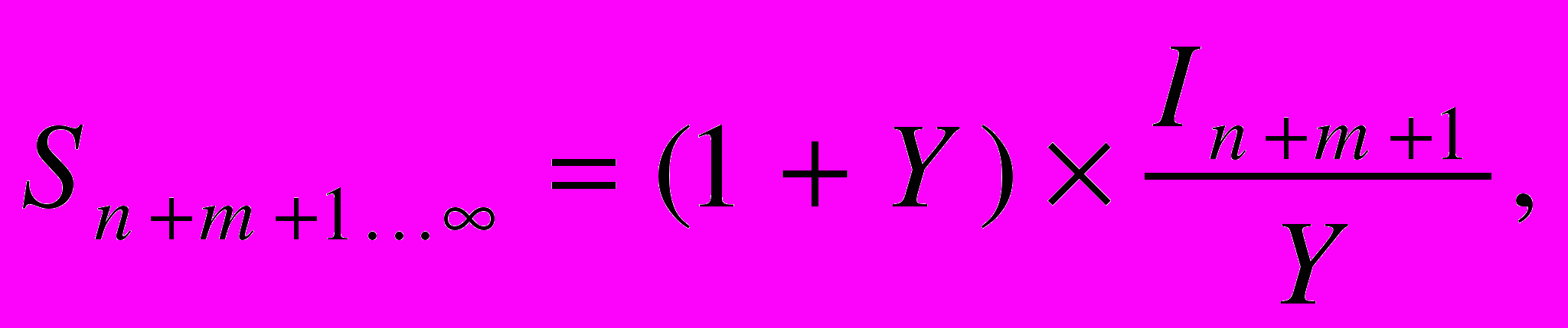
где

n — продолжительность прогнозного периода;

m — продолжительность срока экономической жизни актива в постпрогнозном периоде.

Поскольку поток состоит из постоянных по величине доходов, справедливо выражение

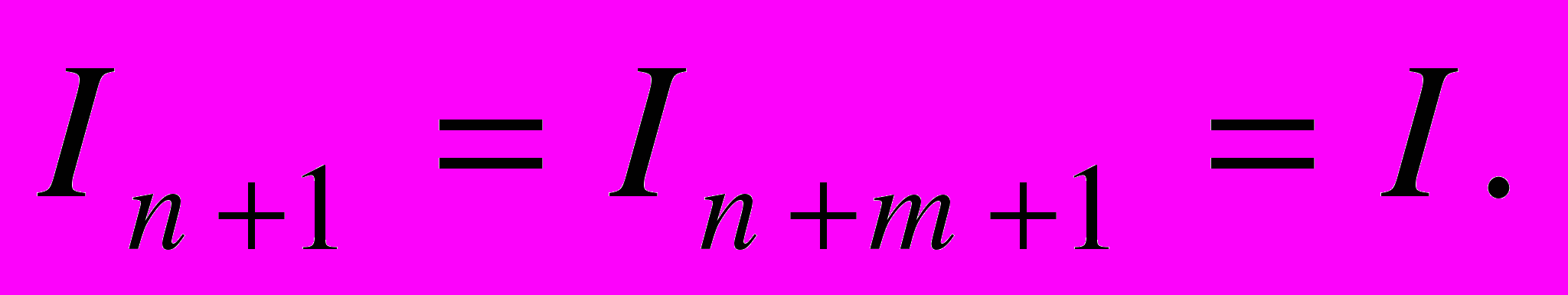
Следовательно, сумма дисконтированного потока доходов в период с 1-го года постпрогнозного периода до года окончания срока жизни актива на момент (n + 1) составляет

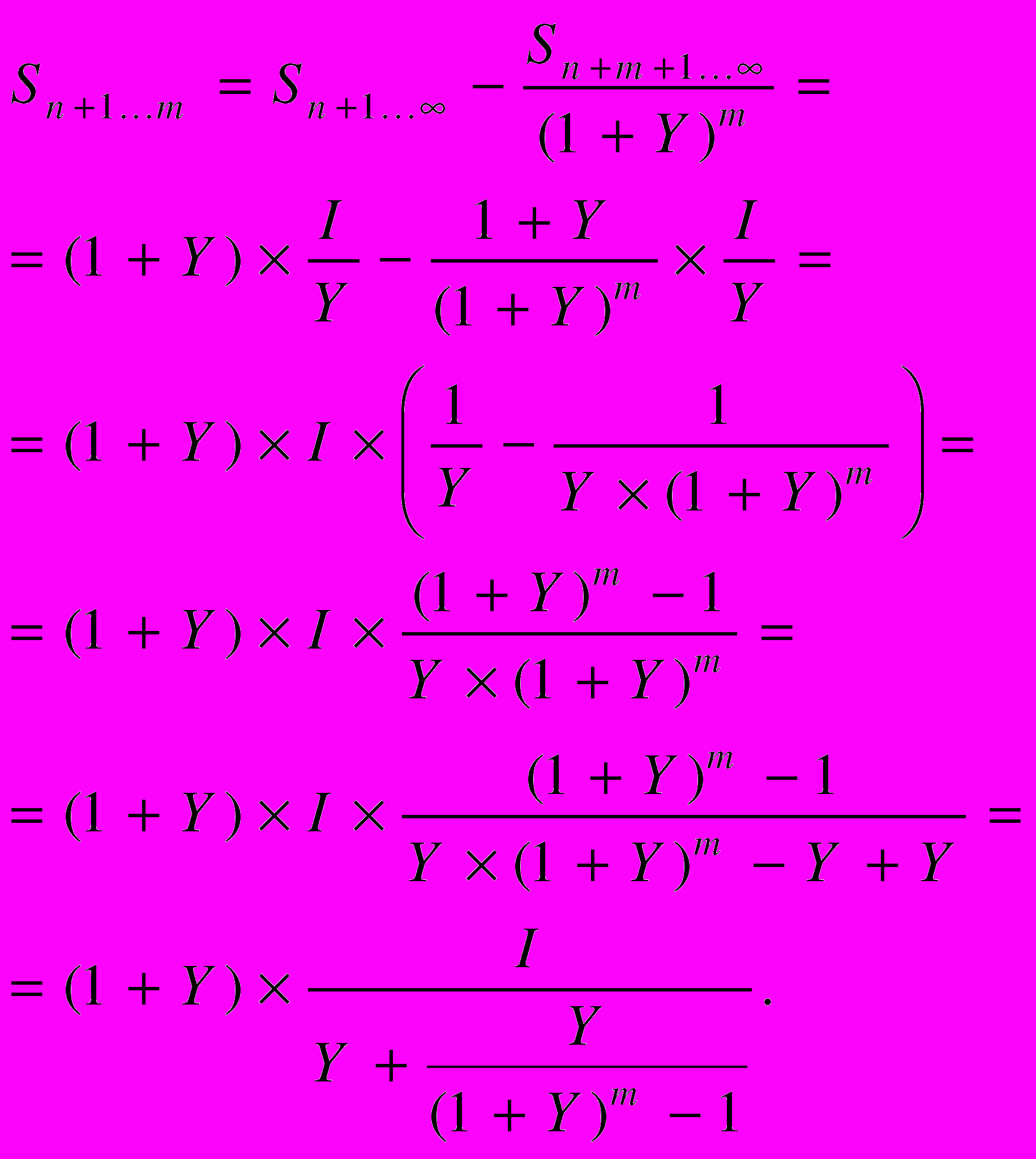
В свою очередь, стоимость реверсии, определенная методом прямой капитализации дохода 1-го года постпрогнозного периода с нормой возврата капитала по методу Инвуда, будет равна

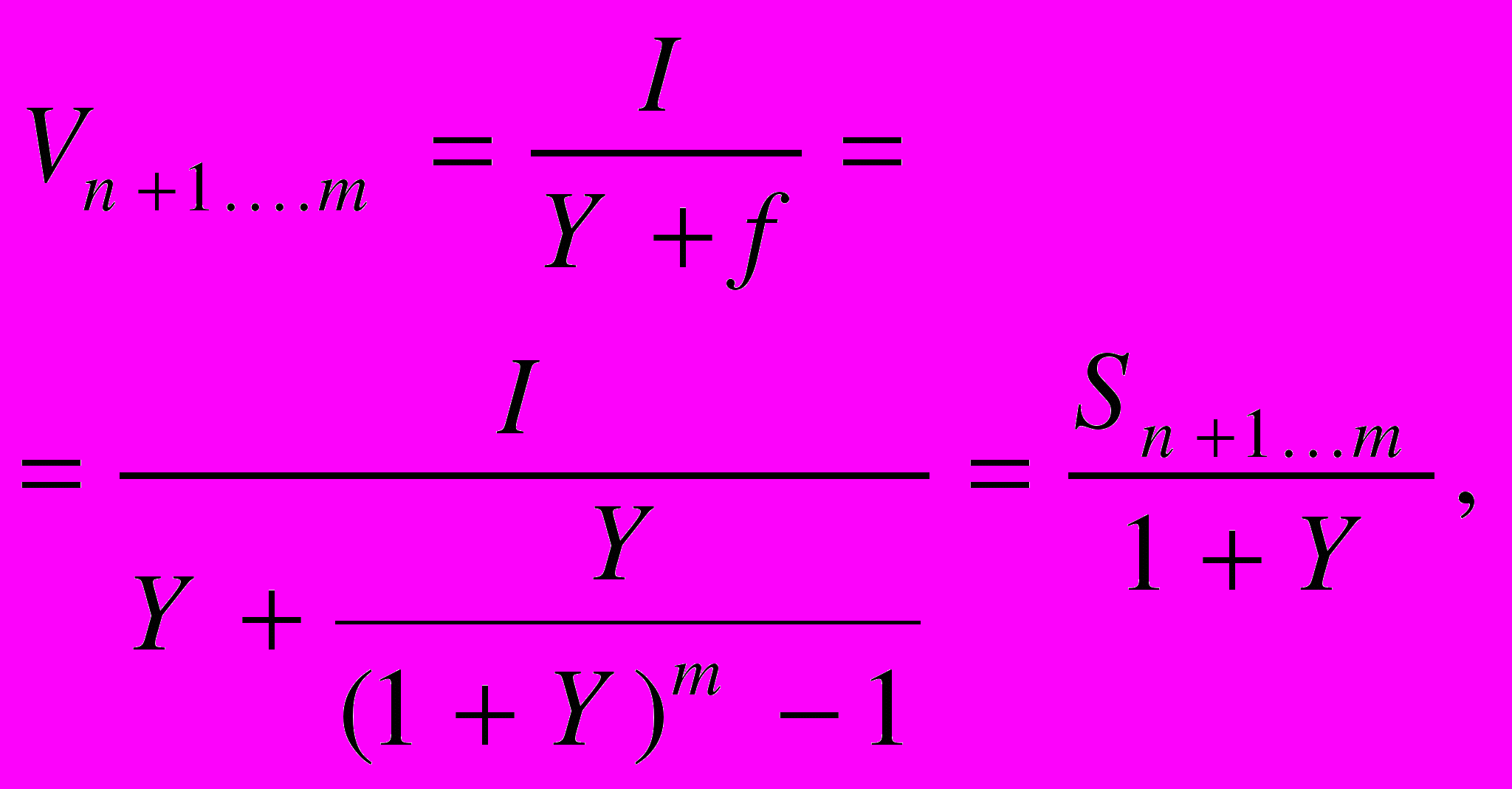
где f — норма возврата капитала.

Деление на (1 + Y) суммы потока доходов в постпрогнозном периоде, дисконтированной на момент получения 1-го дохода этого периода, соответствует дисконтированию на 1 год назад относительно местоположения этого дохода.

Таким образом, в случае дисконтирования при ограниченном во времени потоке постоянных по величине доходов в постпрогнозном периоде должны соблюдаться правила, изложенные выше для бесконечного потока доходов (при условии, что долгосрочный темп изменения величины доходов равен нулю).

Теперь рассмотрим более общий случай для ограниченного во времени потока доходов в постпрогнозном периоде, величина которых изменяется в соответствии с долгосрочным темпом изменения (роста или снижения). При этом, как и в предыдущем случае, выразим сумму ограниченного потока доходов в виде разности сумм бесконечных потоков. Тогда зависимости для расчета указанных сумм (с учетом формулы Фишера) будут иметь вид

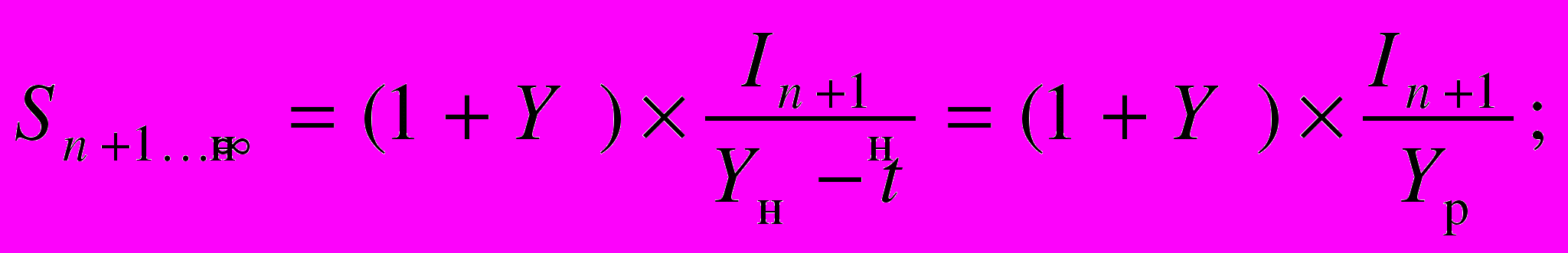
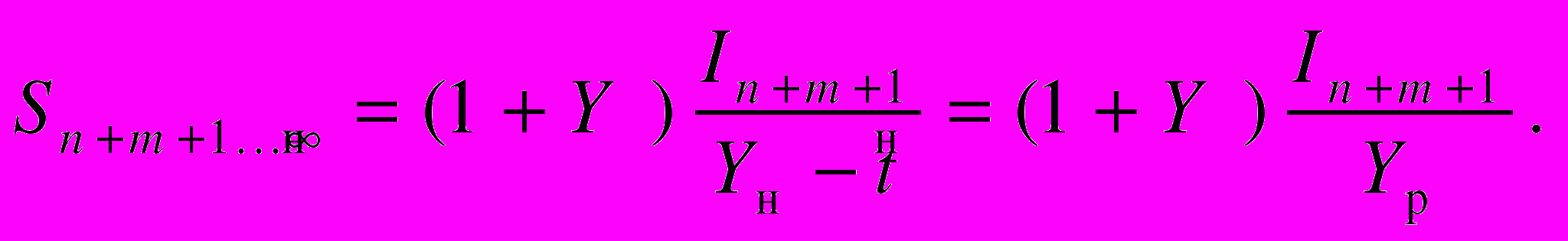
Учитывая, что

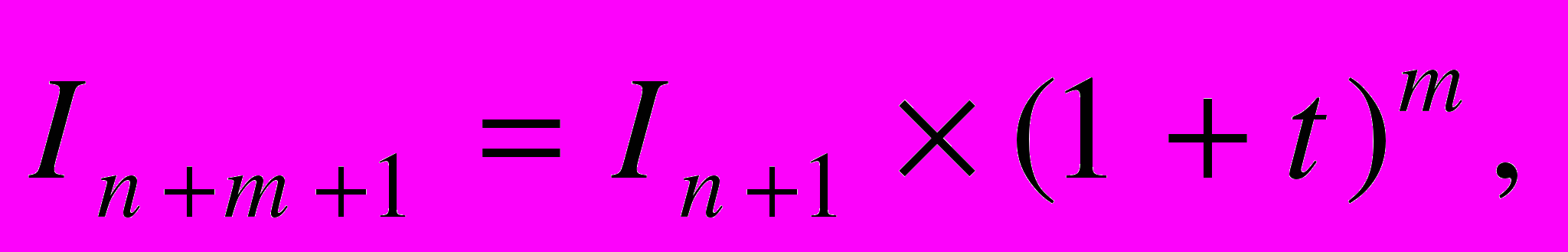получаем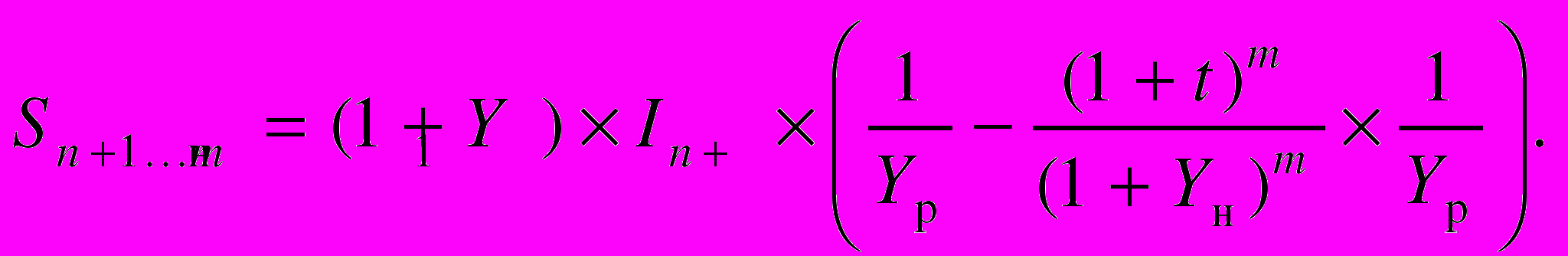

Для величин, значение которых существенно меньше единицы, можно записать соотношение

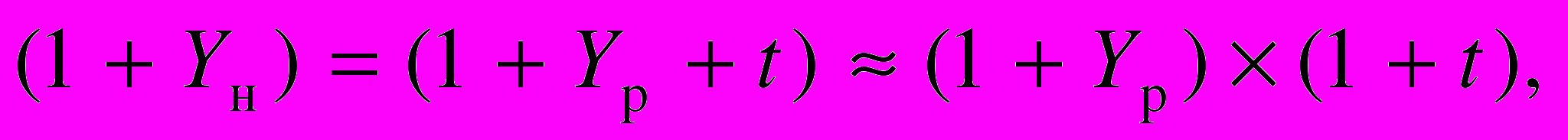(6)

откуда

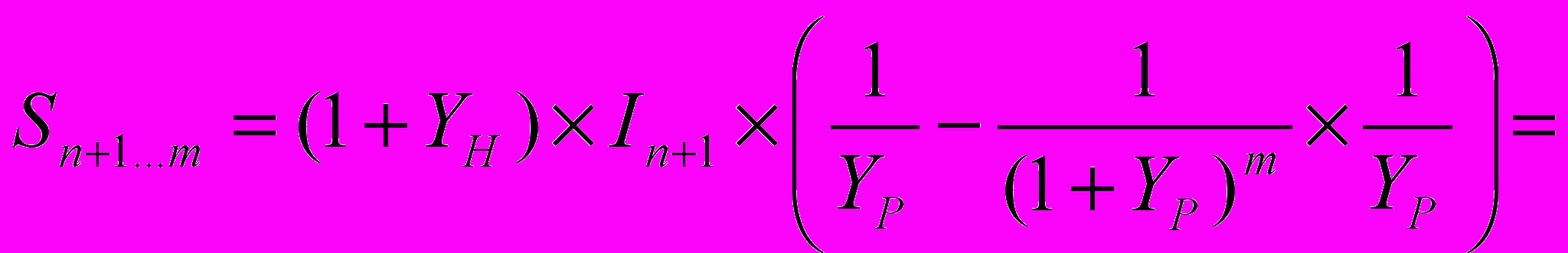
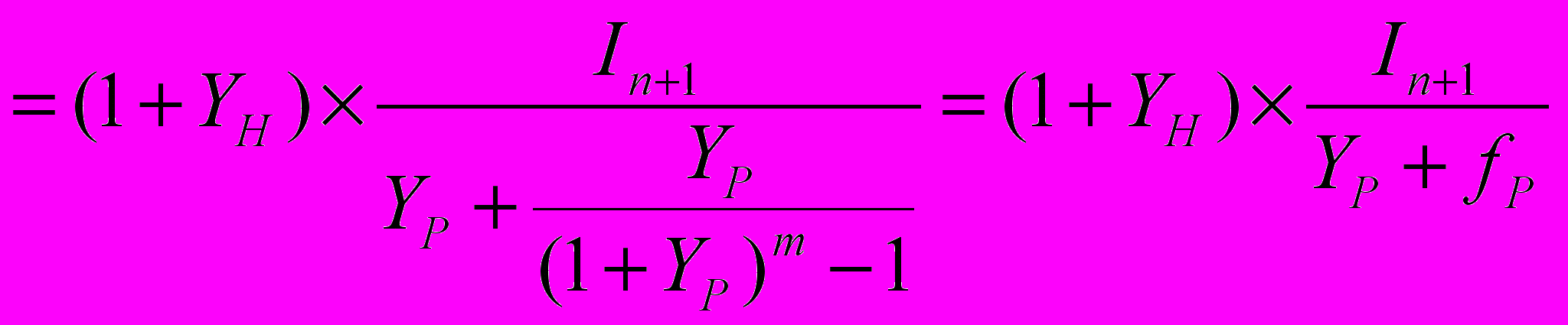
где f_p — норма возврата капитала, рассчитанная по методу Инвуда на основе реальной ставки доходности.

Продисконтировав полученную сумму на 1 год назад и сопоставив полученный результат с формулой расчета стоимости реверсии для ограниченного потока при использовании метода Инвуда для определения нормы возврата капитала, убедимся, что зависимости в точности совпадают при условии расчета стоимости реверсии по реальной ставке доходности. Характерно, что сходные выводы о капитализации по реальной ставке доходности следуют из [3] в отношении земли и из [4, 5] в отношении недвижимости. При этом в методе ДДП дисконтирование потока, состоящего из изменяющихся доходов в прогнозном периоде, и дисконтирование стоимости реверсии должно, как и прежде, осуществляться по номинальной ставке.

Отметим, что все изложенное выше для бесконечного потока в части дисконтирования «на середину периода» и метода ПК полностью распространяется и на рассмотренный случай (с той лишь разницей, что в рассматриваемом случае результаты, полученные методом ПК и методом ДДП, совпадают обычно не точно, а с незначительными погрешностями, что, по-видимому, связано с использованием приближенных зависимостей (5) и (6)). Характерные погрешности для типичных исходных данных приведены в табл. 2. Для сравнения здесь же приведены погрешности расчетов на основе ставки доходности без учета темпов изменения в методе ПК (на основе номинальной ставки доходности).

Таблица 2. Погрешности расчетов при использовании номинальных и реальных ставок доходности

Варианты исходных данных
n	5	5	5	5	5
m	10	10	100	10	10
Y_н, %	10	15	10	10	10
t, %	5	5	5	3	8
Y_p, %	5	10	5	7	2
Погрешность (различия) между результатами расчета стоимости актива по методу ПК и методу ДДП
Стоимость реверсии по Y_p, %	1,63	1,20	0,01	0,87	3,09
Стоимость реверсии по Y_н, %	–14,56	–13,58	–17,19	–9,00	–22,28

Характерно, что выражение для метода Инвуда при расчете нормы возврата капитала было получено на основе разности сумм бесконечных потоков доходов, т. е. без какого-либо допущения о необходимости такого возврата. Следовательно, что этот метод логически объясняется экономической природой инвестиционной деятельности и является основным экономически обоснованным методом расчета нормы возврата капитала. Методы Хоскольда или Ринга обеспечивают совпадение результатов расчетов методом ПК и методом ДДП лишь для фиксированных темпов снижения величины доходов. Поэтому эти методы являются частным случаем и имеют сугубо ограниченное применение. По сути это косвенно подтверждается результатами, приведенными в [6].

Теперь вернемся к приведенному выше логическому умозаключению о необходимости всегда дисконтировать стоимость реверсии на фиксированный период. На первый взгляд, кажется, что обоснованное выше правило о необходимости дисконтирования стоимости реверсии, так же как и доходов прогнозного периода «на середину периода», полностью противоречит указанному умозаключению. Однако поскольку метод ДДП представляет собой лишь математическую модель, описывающую реальные процессы, то изменение условий модели в одной части неизбежно влечет за собой изменение всей модели. Так, правило дисконтирования стоимости реверсии «на конец периода» соответствует модели поступления доходов в конце периода. При смещении доходов в середину года смещается и стоимость реверсии. И этому есть вполне логичное объяснение. Предположим на минуту, что мы не знаем причины переноса годовых доходов на середину года. Например, некто сформулировал нам следующие условия. В прогнозном периоде поступает пять доходов, причем периоды их поступления составляют: 0,5; 1,5; 2,5; 3,5; 4,5. Вполне логично предположить, что 1-й период заканчивается с поступлением 1-го дохода, т. е. в 0,5 года, 2-й период — в 1,5 года и т. д. Следовательно, прогнозный период закачивается в момент поступления 5-го дохода, т. е. в 4,5 года. Далее начинается постпрогнозный период. Именно такую логику подтверждает изложенная выше «математика».

Хочется обратить внимание на то, что все изложенное выше предполагает выполнение следующих условий (допущений):

- ставка доходности в методе ДДП - величина постоянная для прогнозного и постпрогнозного периодов;

- темп роста величины доходов в прогнозном и постпрогнозном периодах – величина постоянная.

Первое допущение привычно оценщикам и не вызывает особых возражений. Однако второе допущение вызывает неприятие, поскольку метод ДДП и применяется, когда поток доходов в прогнозном периоде изменяется самым разным образом. А постоянный темп роста является достаточно редким (идеализированным) случаем. Следовательно напрашивается вывод, что в этом случае метод ПК не применим. Однако присмотримся повнимательнее к этому случаю (при условии дисконтирования «на конец периода»).

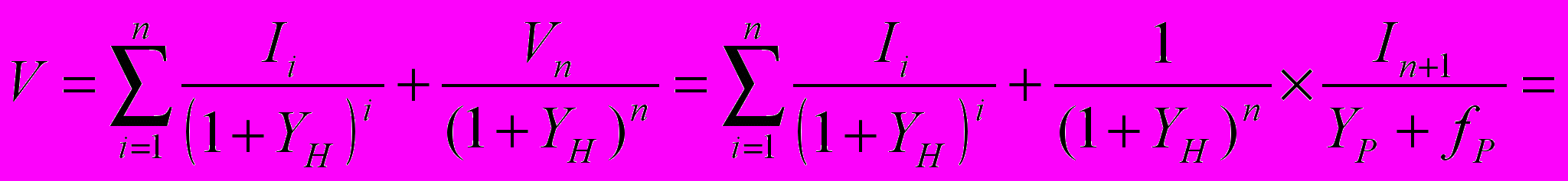
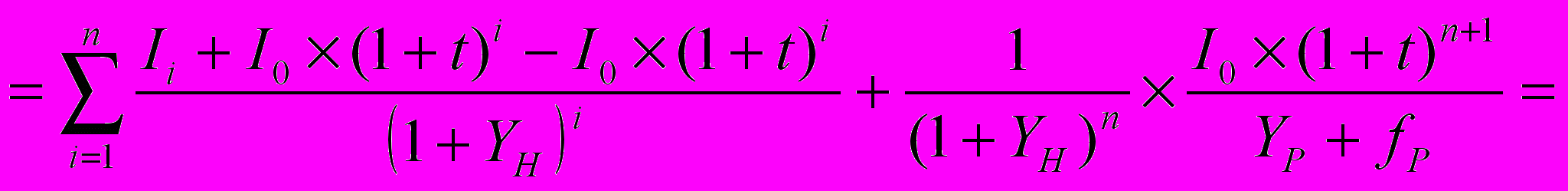
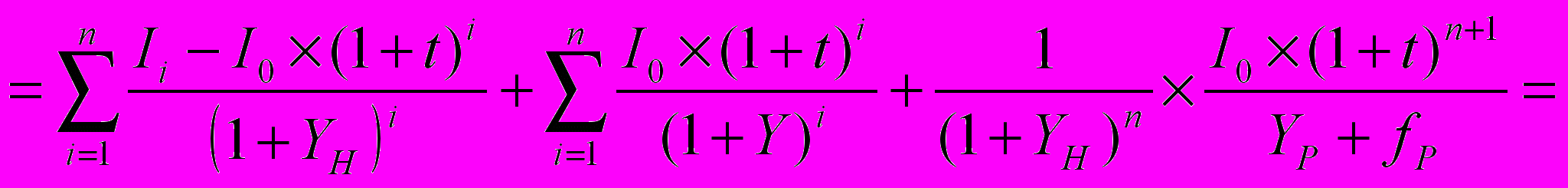
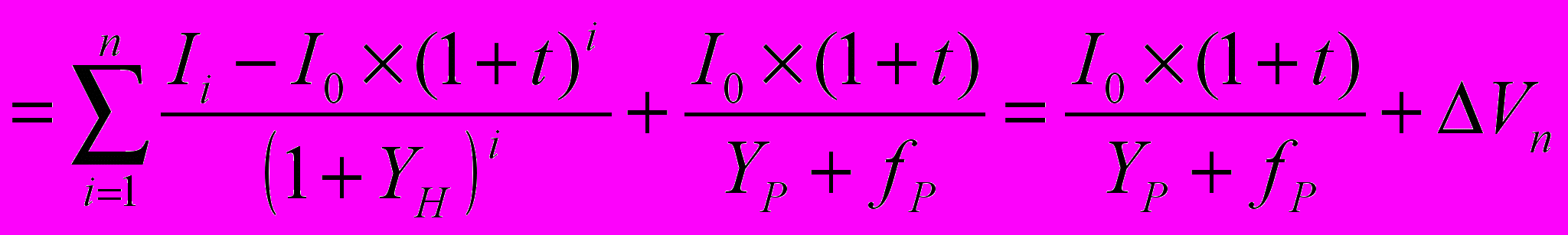(7)

При дисконтировании «на середину периода» зависимость приобретает вид:

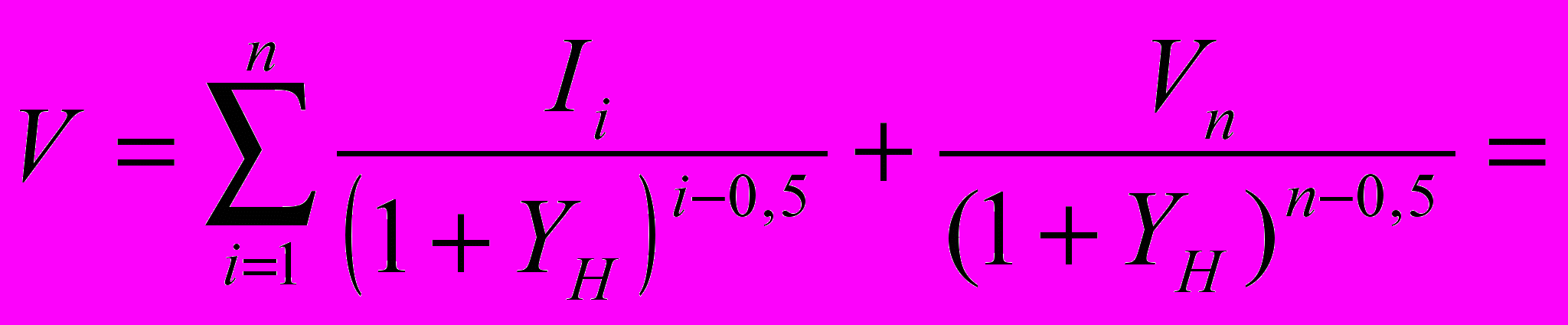
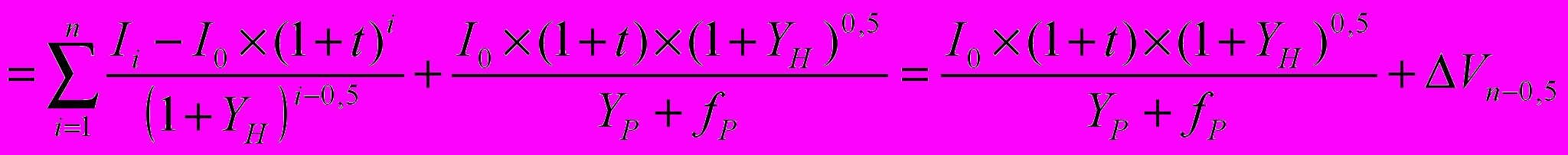(8)

где I₀ – текущая величина годового дохода (на дату оценки);

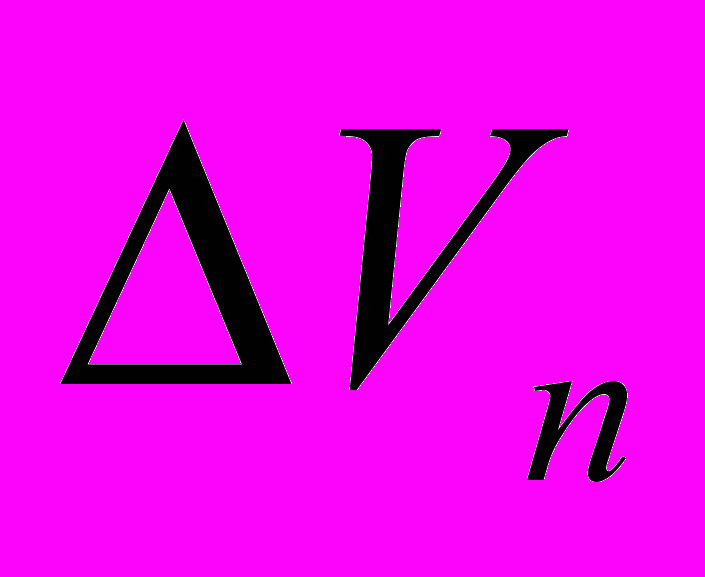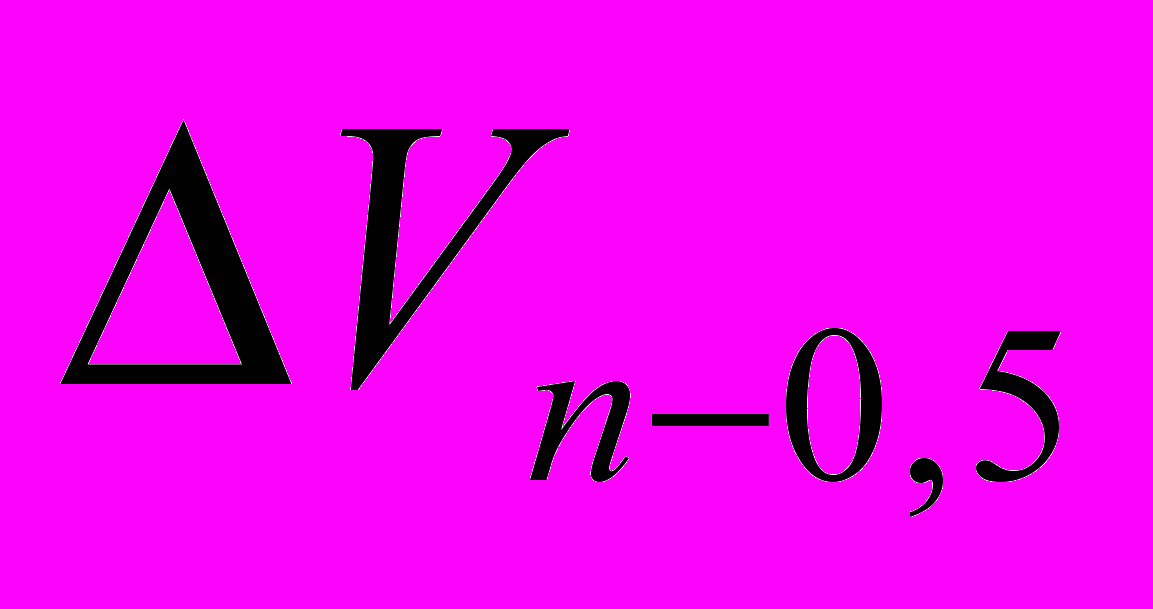— корректировки для метода ПК.

Таким образом, метод ПК может быть использован при любом изменении величины доходов в прогнозном периоде, при условии внесения корректировки.

Следует отметить, что в условиях продолжающегося кризиса в экономике, краткосрочный прогноз (на ближайшие годы) характеризуется высокой неопределенностью, в то время как долгосрочный прогноз (инфляция - темпы роста через десятки лет) с ориентиром на развитые страны в докризисный период представляется более надежным (если верить в перспективу экономического развития страны). Поэтому в настоящее время оценку, например, объекта недвижимости в условиях очевидной необходимости первоначальных капитальных вложений, например на ремонт, целесообразно производить методом ПК с внесением корректировки на эти вложения по зависимостям (7) или (8).

Заключение

На основе изложенного выше можно сформулировать следующие правила.

Правило 1. Вне зависимости от «точки приписки» годового дохода стоимость реверсии дисконтируется на тот же период, что и доход последнего года прогнозного периода, как при бесконечном потоке доходов (не изнашиваемый актив), так и при ограниченном во времени потоке доходов (изнашиваемый актив) в постпрогнозном периоде. В случае дисконтирования «на середину периода» дисконтирование стоимости реверсии во всех случаях должно осуществляться на середину предшествующего года (последнего года прогнозного периода).

Правило 2. При использовании метода ПК капитализируется прогнозная величина дохода, отличающаяся от величины текущего дохода на долгосрочный темп изменения величины этого дохода. Для получения результата, сопоставимого с результатом метода ДДП, во всех случаях капитализации подлежит прогнозное значение дохода, равное величине дохода в 1-й год прогнозного периода, принятого в методе ДДП. Для обеспечения совпадения результатов расчетов методом ПК и методом ДДП (при дисконтировании «на середину периода») в методе ПК капитализироваться должен доход, соответствующий 1-му году прогнозного периода для метода ДДП, скорректированный (умноженный) на квадратный корень из суммы единицы и номинальной ставки доходности.

Строго говоря, это правило справедливо при условии постоянного темпа изменения величины доходов по годам. При невыполнении этого условия, результат метода ПК должен быть дополнительно скорректирован на дисконтированную разность реального потока доходов в прогнозном периоде и потока доходов с постоянным темпом изменения их величины в этом периоде.

Правило 3. Капитализация дохода 1-го года постпрогнозного периода (при расчете стоимости реверсии в методе ДДП) и капитализация прогнозной величины дохода (в методе ПК) должны осуществляться на основе реальной ставки доходности, равной номинальной ставке за вычетом долгосрочного темпа изменения величины доходов. При этом дисконтирование потока состоящего из изменяющихся доходов прогнозного периода и стоимости реверсии в методе ДДП должно осуществляться, как и прежде, на основе номинальной ставки доходности.

Правило 4. При определении нормы возврата капитала для ограниченного и изменяющегося во времени с постоянным темпом потока доходов как в методе ДДП для постпрогнозного периода, так и в методе ПК расчет должен проводиться на основе метода Инвуда с применением реальной ставки доходности. При этом метод Инвуда является основным экономически обоснованным методом расчета нормы возврата капитала при любых постоянных во времени темпах изменения величин доходов. Методы Хоскольда и Ринга имеют сугубо ограниченное применение при фиксированных значениях постоянных темпов снижения величины доходов.

Правило 5. Долгосрочный темп роста величины доходов в методе ПК и для постпрогнозного периода в методе ДДП не может быть равен номинальной ставке доходности или превышать ее.

Литература

1. Оценка имущественных комплексов: Учебник / Под ред. М.И. Кошкиной, Д.В. Подшиваленко, В.И. Светлакова. М.: Экономика, 2007. 318 с.

2. Щербаков В.А., Щербакова Н.А. Оценка стоимости предприятия (бизнеса). М.: Омега-Л, 2006. 106 с.

3. Зельдин М.А., Грибовский С.В., Баринов Н.П. Оценка величины рыночной арендной платы за пользование земельным участком // Имущественные отношения в Российской Федерации. 2009. № 6.

4. Фоменко А.Н. Особенности применения модели Гордона при оценке стоимости объектов недвижимости. — www.anf-ocenka.narod.ru

5. Смоляк С.А. Метод прямой капитализации доходов при оценке недвижимости // Вопросы оценки. 2009. № 1.

6. Лейфер Л.А. Метод прямой капитализации. Обобщенная модель Инвуда. — www.labrate.ru/leifer

Фоменко Александр Никифорович, e-mail: anf-ocenka@mail.ru

Опубликована: Вопросы оценки №2, 2011, стр. 48

Blog

А. Н. Фоменко, канд техн наук

Содержание