Связь солнечной активности с Юпитером и Сатурном
| Вид материала | Документы |
СодержаниеДва замечания |
- 1. Солнечная активность, 192.05kb.
- История изучения солнечной активности, 144.74kb.
- Колебания солнечной активности – основной климатообразующий фактор в масштабе тысячелетия, 115.69kb.
- Малые тела Солнечной системы. Астероиды, 118.46kb.
- Влияние солнечной активности на биологические объекты, 1269.11kb.
- Динамика Солнечной системы, 11.55kb.
- Комитет по образованию г. Улан-Удэ, 180.31kb.
- Строение Солнечной системы, 248.93kb.
- Некоторые нерешенные вопросы в исследовании сенсорной системы у человека и ее обусловленности, 144.69kb.
- К вопросу о характере и механизмах влияния солнечной активности и космических лучей, 109.91kb.
Связь солнечной активности с Юпитером и Сатурном.
Л.А.Соловьева.
Предлагается новая версия связи солнечной активности с орбитами Юпитера и Сатурна.
Было замечено, что некоторые даты максимальной солнечной активности отличаются друг от друга на целое число периодов Юпитера и Сатурна.
Предполагается существование роя метеорных тел, орбита которого находится между орбитами Юпитера и Сатурна.
При сближении планет с роем, его тела покидают свою орбиту и летят во все стороны, в виде облака, в том числе, и прямо на Солнце, увеличивая солнечную активность и число болидов на Земле.
В нечетные циклы, в годы, близкие к максимальной солнечной активности, болиды регистрируются на Земле в 2-3 раза чаще, чем в годы минимальной солнечной активности.
До сих пор не все ясно в природе солнечной активности.
В версии приливной силы от Юпитера и Сатурна [1,2] выявлены 11-ти и 100-летние периоды СА, но никакой фазовой корреляции с планетами не обнаружено.
Автором было замечено, что некоторые даты максимальной солнечной активности (ТСА) отличаются между собой на целое число периодов обращения выше названных планет вокруг Солнца.
Это дает основание полагать, что эти планеты в определенных местах своих орбит влияют на солнечную активность, но не каждый раз. Например, Юпитер за 250 лет (с 1727 по 1979,5 года) обернулся вокруг Солнца 21 раз. Из них только 8 раз (табл. 1а, столбец 2 ) был связан с ТСА , а Сатурн за 210 лет (с 1727 по 1937 гг..) прошел по своей орбите 7 раз и только 4 раза был связан с ТСА (табл. 1б , столб.2).
Кроме того, в даты, связанные с Юпитером и Сатурном, солнечная активность была достаточно высокой и числа Вольфа были больше 80W.
Таким образом, на каком-то определенном месте орбит планет появляются иногда условия для увеличения солнечной активности.
Связь даты максимальной солнечной активности с периодом Юпитера (11.86 г).
Таблица 1а.
| № цикла | Дата максимальной СА | Разность r ТСА = ТСА - ТО | Число периодов | n ∙ 11.86 | Отклонение rТСА - n∙РЮ |
| | ТСА | rТСА | n | n∙PЮ | Δ r ТС А |
| 1 | 2 | 3 | 4 | 5 | 6 |
| | ТО= 1727,2 | | 1 | 11,86 | |
| | 1750,3 | 23,1 | 2 | 23,7 | 0,6 |
| | 88,1 | 60,9 | 5 | 59,3 | +1,6 |
| 9 | 1848,1 | 120,9 | 10 | 118,6 | +2,3 |
| 11 | 70,6 | 143,4 | 12 | 142,3 | +1,1 |
| 13 | 94,1 | 166,9 | 14 | 166,1 | +0,8 |
| 15 | 1917,6 | 190,4 | 16 | 189,8 | +0,6 |
| 21 | 79,5 | 252,3 | 21 | 249,1 | +3,2 |
(ΔrТСА)ср.= +1,1
Связь даты максимальной солнечной активности с периодом Сатурна (29, 5 г)
Таблица 1б
| № цикла | Дата макс. СА | Разность r ТСА – ТО | Число периодов | n·29,5 | Отклонение r TСА - n∙PC· |
| | ТСА | rTCA | n | n∙PC | |
| 1 | 2 | 3 | 4 | 5 | 6 |
| | ТО=1727,2 | | 1 | 29,5 | |
| | 1788,1 | 60,9 | 2 | 59,0 | +1,9 |
| 9 | 1848,1 | 120,9 | 4 | 118,0 | +2,9 |
| 17 | 1937,4 | 210,2 | 7 | 206,5 | +3,7 |
(ΔrТСА)ср= +2,1
Пояснения к табл. 1а и 1б.
Столбец 2 – даты ТСА - максимальной СА, связанные с орбитами Юпитера и Сатурна.
Столбец 3 – разность дат в годах. За ТО выбрана дата, первая из столбца 2 (табл.1а и 1б), чтобы все разности r ТCA были положительными.
Столбец 5 – целое число периодов Юпитера и Сатурна, близкое к данным столбца 3.
Столбец 6 – разность чисел из столбцов 3 и 5, т.е. отклонения rТСА от целого числа периодов планет. Следует заметить, что все значения ТСА – из нечетных циклов.
Для объяснения связи солнечной активности с положениями Юпитера и Сатурна на их орбитах, автором предложена версия о существования роя метеорных тел (назовем его Меро), орбита которого находится между орбитами Юпитера и Сатурна.
При сближении Меро с планетами, тела Меро покидают свою орбиту и летят во все стороны в виде облака, в том числе и прямо на Солнце, увеличивая его активность, и на Землю, увеличивая число болидов. Сближение Меро с планетами происходит вблизи узлов орбиты Меро. Даты ТСА (табл.1а и 1б, столбец 2) связаны с одним узлом Меро, второй узел отличается от первого на половину периодов Юпитера и Сатурна.
В учебнике по астрономии С.Н. Блажко [4] пишет, что “постоянного периода между соседними максимумами СА нет… промежуток между ними колеблется между 7 и 17 годами; в среднем он равен 11,1 года”.
Возможно, между 1788,1 и 1805,2 г.г. был не один, а два цикла.
Но за последние 150 лет период солнечной активности стал более стабильным, поэтому для определения узлов орбиты Меро, были взяты данные от 1840 до 1986 г.
На рис.1 кроме основных максимумов СА (М) заметны ещё вторичные максимумы (m), которые, видимо, являются отражением либрационных точек орбиты Меро.
Для того, чтобы определить узлы орбиты Меро, посмотрим какие связи существуют между остальными датами максимумов солнечной активности (M и m) (Табл. 2).
Таблица 2, в столбцах:
1 – номера циклов СА;
2 – числа Вольфа (W);
3 и 4 – даты максимумов СА (М и m) нечетных и четных циклов;
5 - Δ 1 - разность даты ТСА нечетного цикла СА и даты ближайшего предшествующего афелия Юпитера;
6 - Δ 2 - разность ТСА четного цикла СА и даты ближайшего предшествующего перигелия Юпитера;
7 - Δ 3 - разность ТСА нечетного цикла СА и даты ближайшего предшествующего перигелия Сатурна;
8 - Δ 4 - разность ТСА четного цикла СА и даты ближайшего предшествующего афелия Сатурна, ближайшего к дате ТСА;
9,10 - наличие сближения Меро с планетами отмечены крестом.
Буквой m обозначены даты и значения Δi вторичных максимумов на табл.2.
Афелии и перигелии планет, возможно, не совсем точно вычислены, но главное, моменты афелия и перигелия отличаются между собой на целое число периодов, а столбцы афелия со столбцами перигелия отличаются еще на половину периодов планет. Постоянные погрешности для всего периода (1840-1986 гг.) для данной задачи не имеют значения, так как здесь определяется только кучность значений Δi, которая определяет существование узлов орбиты Меро.
Расписание движения планет по орбитам является здесь равномерной шкалой времени. Все вариации периода солнечной активности определяются нестабильностью периода Меро. Наибольшее влияние на Меро Юпитер оказывает, когда он в афелии, а Сатурн в перигелии. В этих случаях планеты могут сблизиться с Меро на кратчайшее расстояние.
Наибольшее число дат ТСА, связанных с периодами выше указанных планет, оказалось в нечетных циклах СА.
И действительно, за период с 1840 по 1980 гг.. сближение Меро с Юпитером было семь раз (пять в нечетные и два в четные циклы) и шесть сближений с Сатурном (четыре в нечетные и два в четные циклы). Смотри рис. 2, 3.
Значение разности даты ТСА и положения планеты на орбите я называю проекцией даты ТСА на орбиту. Например, в 9ом цикле СА, значение Δ1 равно 8,9 года. Это значит, что когда наступила максимальная солнечная активность (1848,1 г.) Юпитер отошел от своего афелия на 8,9 года (по орбите с периодом 11,9 года), а в четный 18й цикл (в 1947,5 г.) Δ2 равно 7,5 года, т.е. в дату максимальной солнечной активности в 1947,5 г. Юпитер отошел от своего перигелия на 7,5 года. На рис. 2 и 3 показано как расположились даты ТСА на орбите Юпитера и Сатурна.
Значения Δ1 и Δ2 в среднем оказались равны 7,7, а Δ3 и Δ4 - 17,3 года. Эти же значения по вторичным максимумам равны 7,5 и 19.9 года (что в пределах точности определения практически совпадают), то есть вторичные максимумы (m), видимо, отражают либрационные точки орбиты Меро.

* * *

* * *
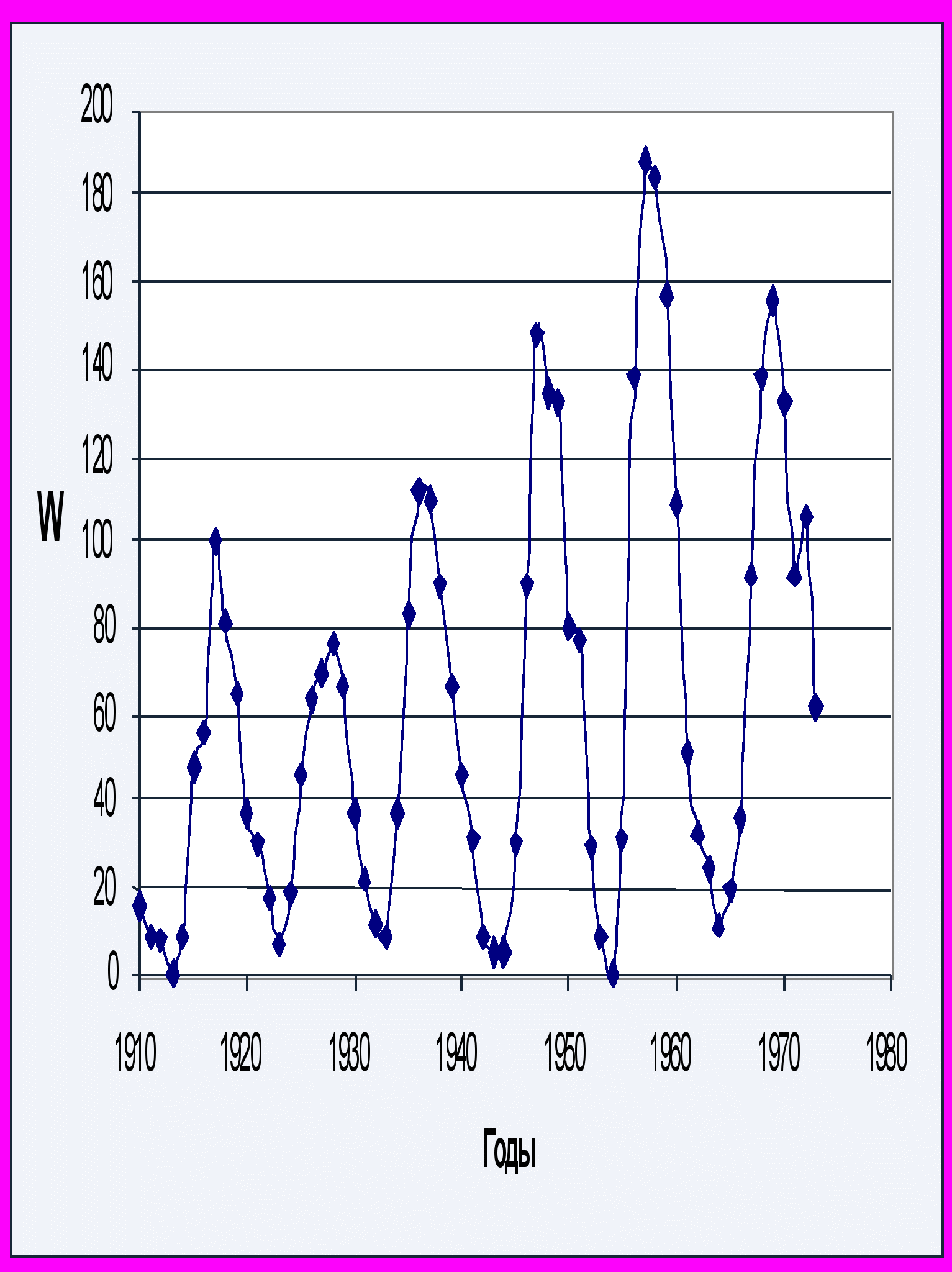
Рис.1. Изменения чисел Вольфа (W) за 140 лет с 1840 по 1980 гг [3];
Знаком ( • ) обозначено сближение Меро с Юпитером;
Знаком ( * ) обозначено сближение Меро с Сатурном (столбецы 9 и 10 табл.2).
Определение проекции узлов орбиты Меро на орбиты Юпитера и Сатурна.
Таблица 2.
| № цикла | Числа Воль-фа | Дата максимальной СА ТСА | ТСА – ТЮ | ТСА - ТС | Сбли-жение Меро с плане-тами | При-меча-ние | ||||
| № | W | Нечет. | Четн. | ∆1 | ∆2 | ∆3 | ∆4 | Ю | С | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 9 | 125 | 1848,1 | | +8,9 | | +20,8 | | + | + | |
| | | 51,5m | | (+0,5m) | | +24,2m | | | +m | |
| 10 | 98 | | 60,1 | | (+3,1) | | 17,9 | | + | |
| | | | 64,0m | | +7,0m | | +21,8m | +m | +m | |
| 11 | 140 | 70,6 | | +7,7 | | +13,8 | | + | + | |
| | | 72,0m | | +9,1m | | +15,2m | | +m | +m | |
| 12 | 65 | | 83,9 | | (+3,2) | | (+12,3) | | | W<80 |
| 13 | 85 | 94,1 | | +7,5 | | (+7,8) | | + | | |
| 14 | 65 | | 1907,0 | | (+2,6) | | (+5,9) | | | W<80 |
| | | 1915,6m | | +5,2m | | (-0,2) | | +m | | |
| 15 | 107 | 17,6 | | +7,2 | | (+1,8) | | + | | |
| 16 | 78 | | 28,4 | | (+0,3) | | (+27,3) | | | W<80 |
| 17 | 115 | 37,4 | | (+3,3) | | +21,6 | | | + | |
| 18 | 145 | | 47,5 | | +7,5 | | +16,9 | + | + | |
| | | | 49,0m | | +9,0m | | +18,4m | +m | +m | |
| 19 | 185 | 57,9 | | (+0,1) | | +12,6 | | | + | |
| 20 | 105 | | 68,9 | | +5,2 | | (+8,8) | + | | |
| | | | 71,0m | | +7,3m | | (+10,9m) | +m | | |
| 21 | 155 | 79,5 | | +9,8 | | (+4,7) | | + | | |
| | | | ∆iср n nm | 8,2 7,2 5 2m | 6,4 7,8 2 3m | 17,2 19,7 4 2m | 17,4 20 2 2m | | | |
n – число сближений Меро с планетами.
nm – число сближений либрационных точек Меро с планетами.
Р

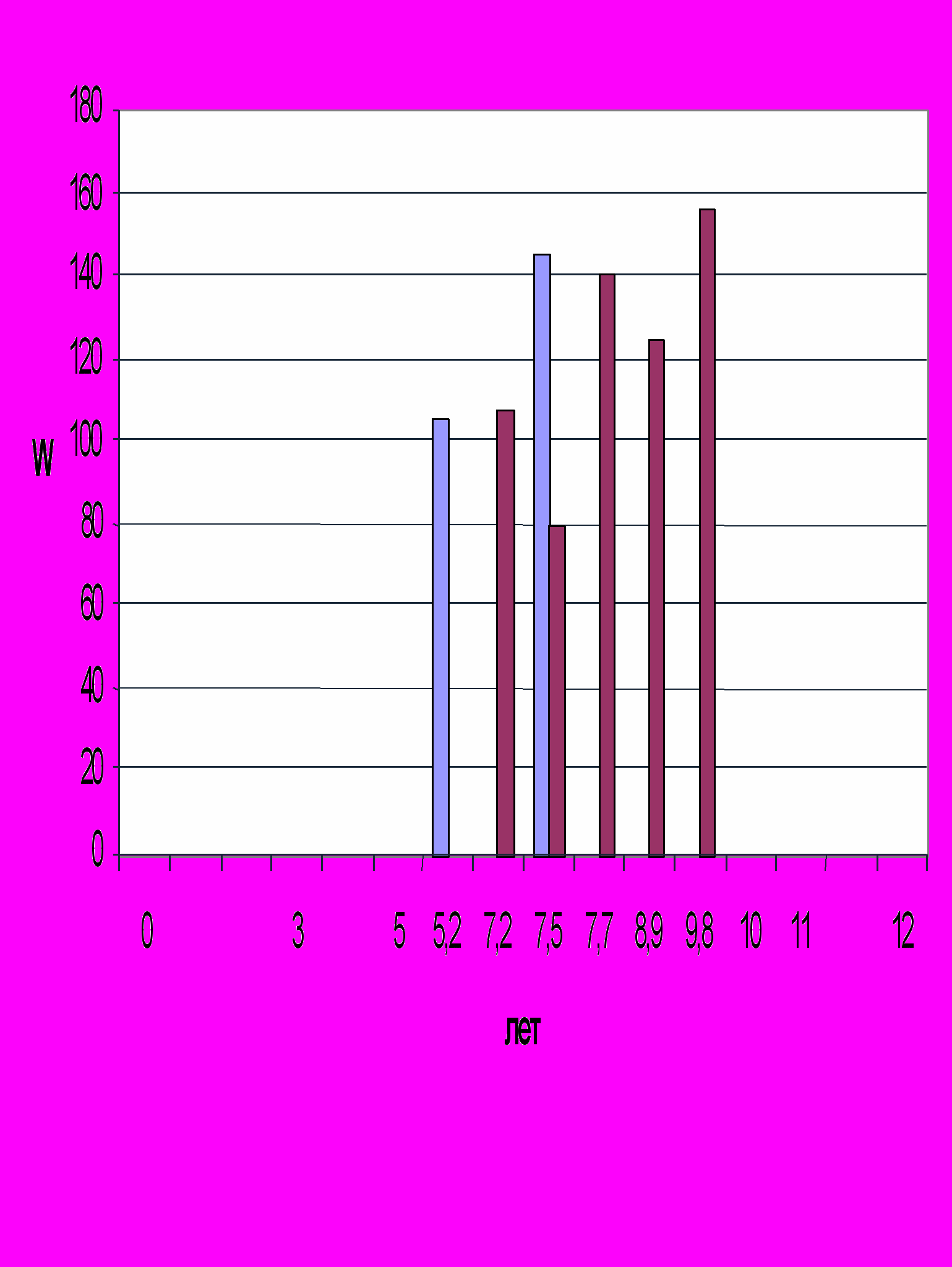
 ис. 2. Проекция дат максимальной солнечной активности ТСА ( - четные и - нечетные циклы) на орбиту Юпитера.
ис. 2. Проекция дат максимальной солнечной активности ТСА ( - четные и - нечетные циклы) на орбиту Юпитера. №№ циклов в порядке возрастания значений Δ1 и Δ2:
+ - Δ1: 15, 13, 11, 9, 21
· - Δ2: 20, 18
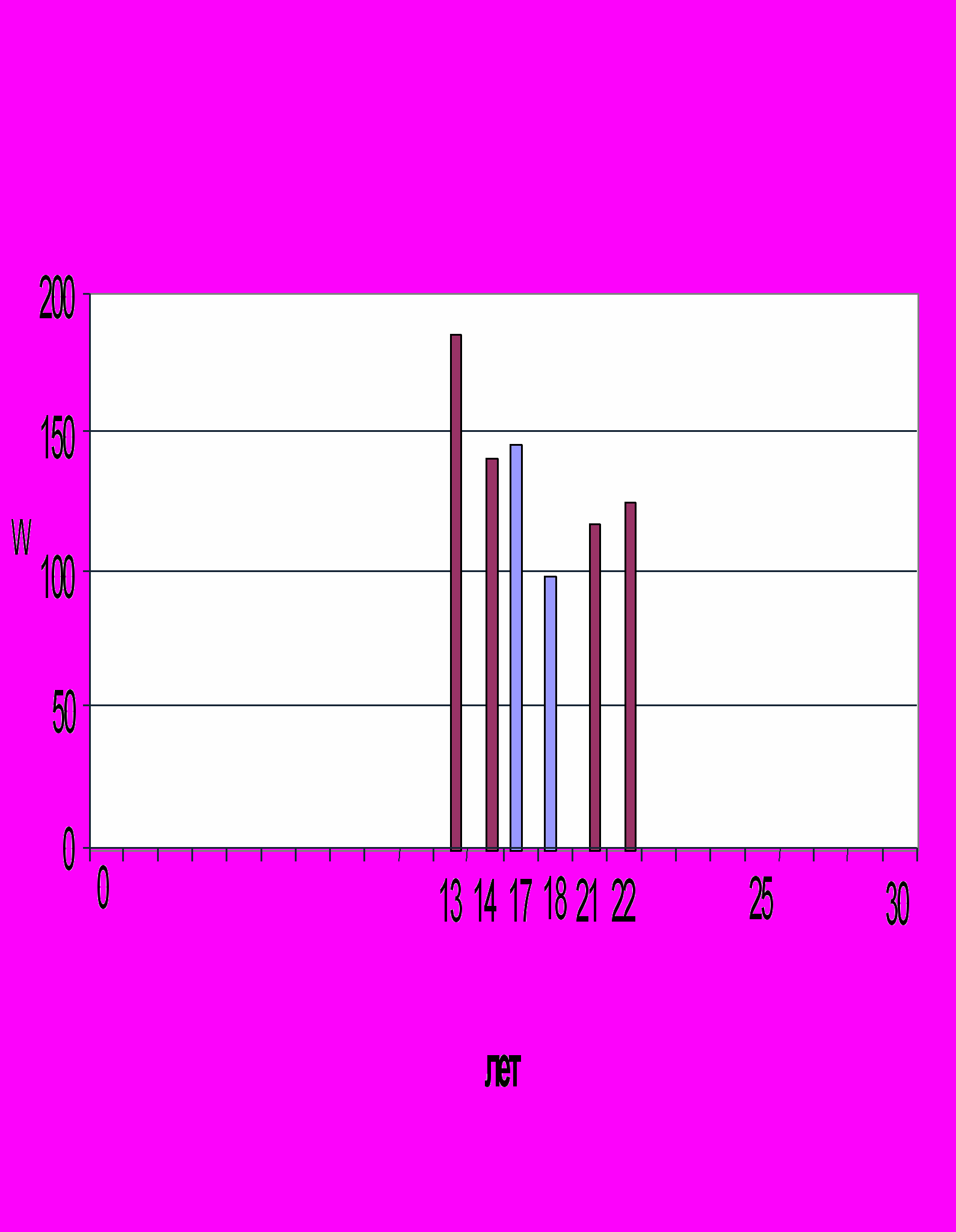
Р

 ис. 3. Проекция дат максимальной солнечной активности ТСА ( - четные и - нечетные циклы) на орбиту Сатурна: Δ3: 19, 11, 9, 17
ис. 3. Проекция дат максимальной солнечной активности ТСА ( - четные и - нечетные циклы) на орбиту Сатурна: Δ3: 19, 11, 9, 17Δ4: 18, 10
Е.И.Казимирчак-Полонская, исследуя движения комет, показала, что Юпитер и Сатурн, при сближении с кометой меняют элементы её орбиты существенным образом: “Юпитер начинает оказывать сильное возмущающее воздействие на кометную орбиту еще задолго до входа кометы в сферу его действия” [5].
Может быть дальнодействием Юпитера и Сатурна можно объяснить солнечную активность в годы, когда не было сближения Меро с планетами. В циклы 12-й, 14-й и 16-й максимальная солнечная активность была, хотя и слабая, но четко определена.
Еще один факт вызывает удивление: сближение Меро с планетами происходило в 2 раза чаще в даты нечетных циклов СА (рис. 2 и 3). Разброс проекций узлов Меро на орбиты Юпитера (на 140˚) и Сатурна (110˚) возможно обусловлен влиянием огромных масс Юпитера и Сатурна, но все же значения Δi раскинулись не на все 360° орбит, а расположились достаточно кучно, т.е. неслучайным образом. Можно прийти к выводу, что узлы Меро существуют и связь солнечной активности с орбитами Юпитера и Сатурна осуществляется через рой Меро.
Для подтверждения этого вывода рассмотрим существующие связи числа болидов с солнечной активностью, так как метеорный рой Меро должен проявить себя еще и в результатах регистрации болидов на Земле.
В комитет по метеоритам АН СССР [8] было сообщено о 1917 болидах. Числа S ежегодных сообщений были сгруппированы по близости года их наблюдений ТН к году максимальной солнечной активности ТСА. Обозначим через τ разность ТН - ТСА.
На рис. 4 приведены распределения числа болидов для четных и нечетных циклов СА. Оказалось, что в нечетные циклы СА максимальное число болидов совпадает с ТСА (τ =0). В четные циклы максимальное число болидов наступило раньше на 2 года. Кроме того, среднее число болидов в циклах различно. В четный цикл СА, в годы, близкие к ТСА (ТСА ± 1 год) болидов оказалось в два раза меньше, чем в нечетные циклы СА.
По данным Прерийной болидной сети [11] в четный цикл 1965 – 1975 гг.. максимальное число болидов с большой фотометрической массой метеорного тела М∞ было зафиксировано (в1966,8 г.) за 2 года до максимальной СА (ТСА= 1968,9 г.). На рис.5 показаны числа n ярких болидов. Это согласуется с рис. 4, кривая 2.
В четные циклы, в годы, близкие к ТСА, числа болидов заметно увеличены зимой. На рис.9 приведены их средние значения (кривая 1).
Для уточнения полученной корреляционной связи СА и числа болидов, автором был составлен каталог ярких (< - 6m.) болидов [9]. Каталог содержит около 600 болидов и метеоритов. Для определения отличия числа болидов в четные и нечетные циклы СА были взяты данные за 19 век, а в 20 веке - только за целые циклы СА (до 1975 г.). За 19 век было зафиксировано по 2 болида в год, а за период 1900-1975гг – по 5 болидов.
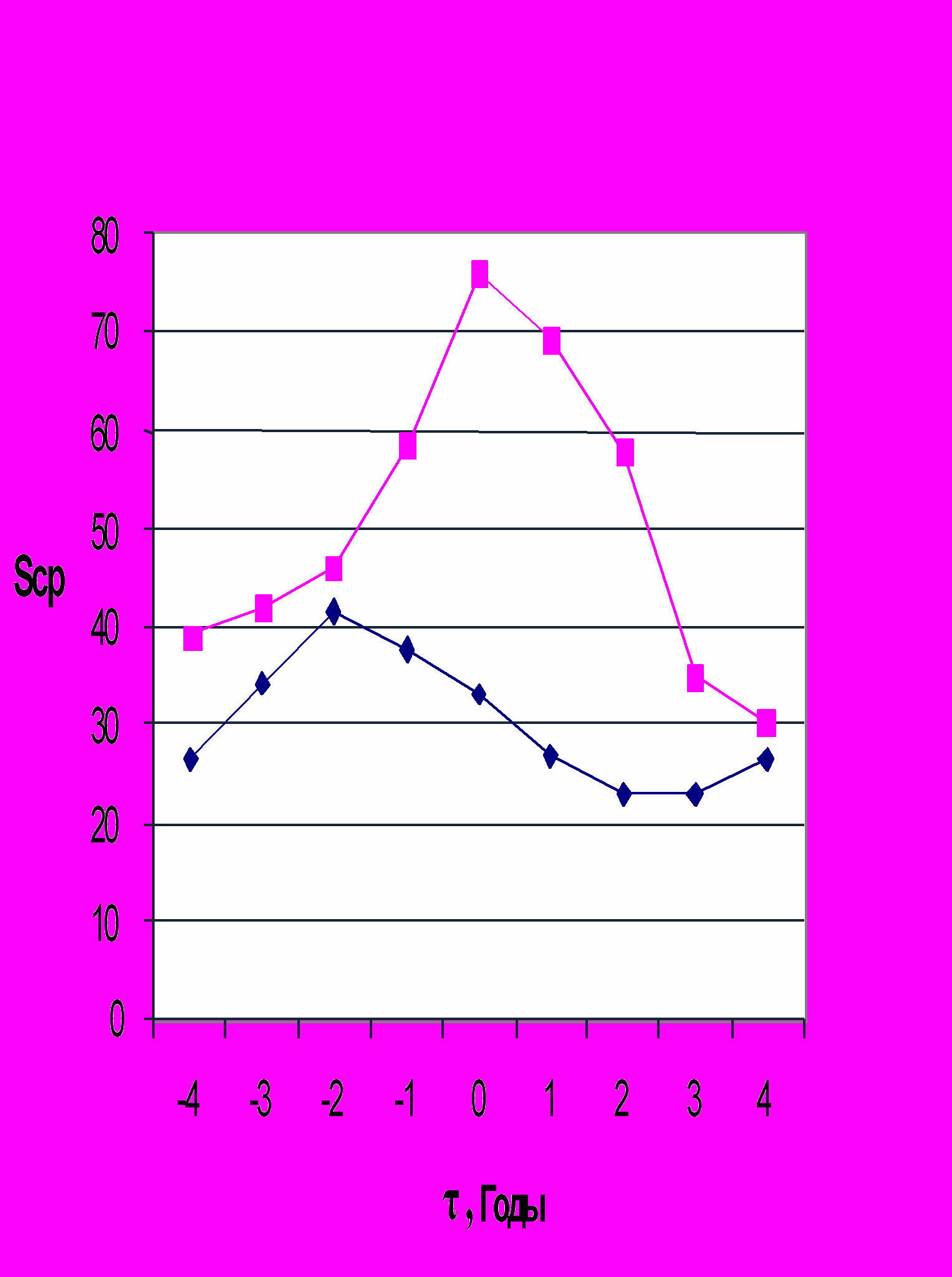
Рис.4. Распределение числа болидов в зависимости от близости τ года их регистрации к максимальной СА.[8].
- ▄ нечетные циклы n = 1024 (22 года);
- ♦ четные циклы n = 833 (29лет);
τ =0 – год максимальной СА; τ = ТН – ТСА.
Sср. – скользящее среднее по 3 года.
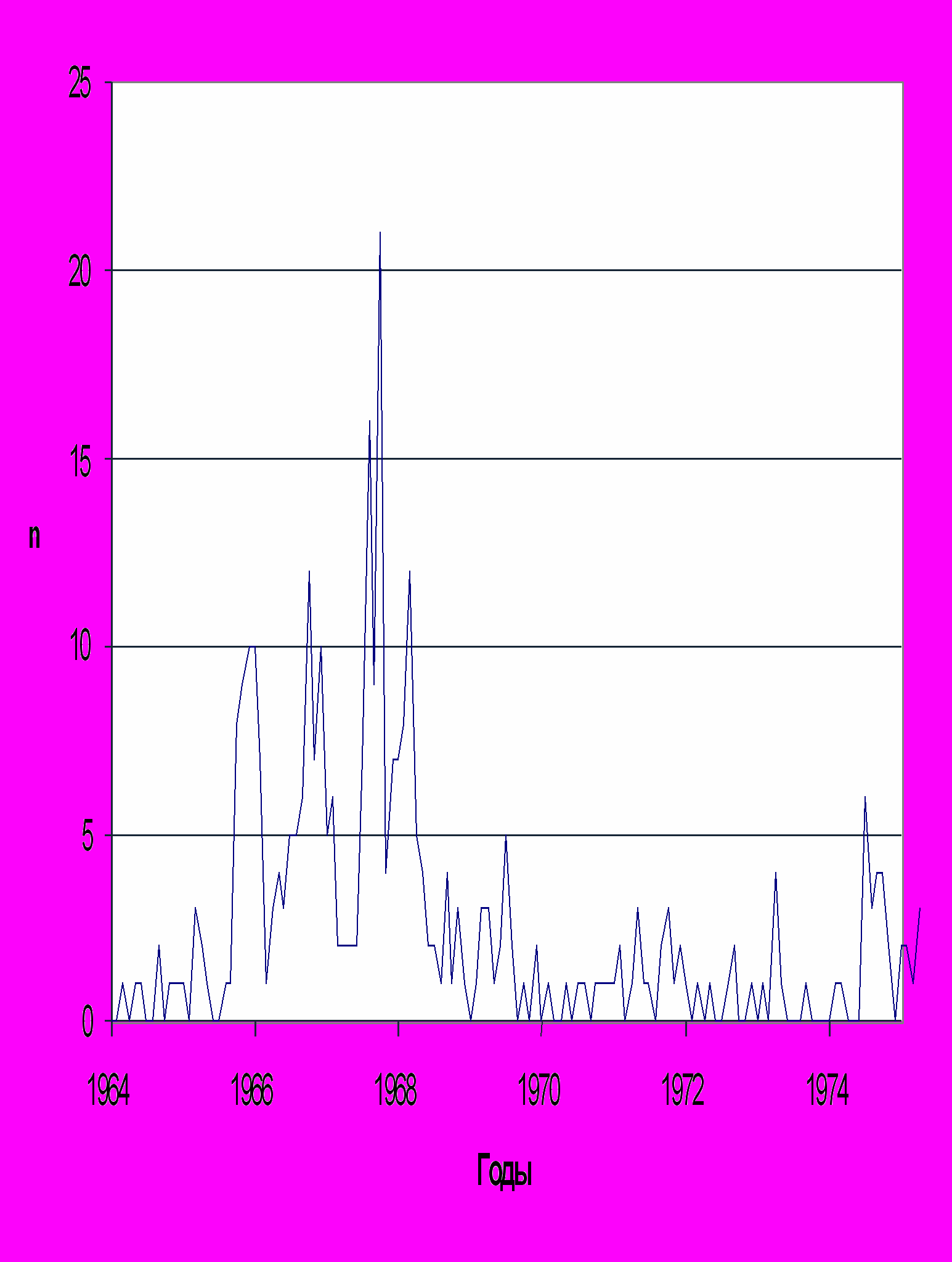
Рис.5. Число n ярких болидов (М∞ > 5 кг) Прерийной болидной сети за четный цикл СА (1965 – 1975 гг.) [11].
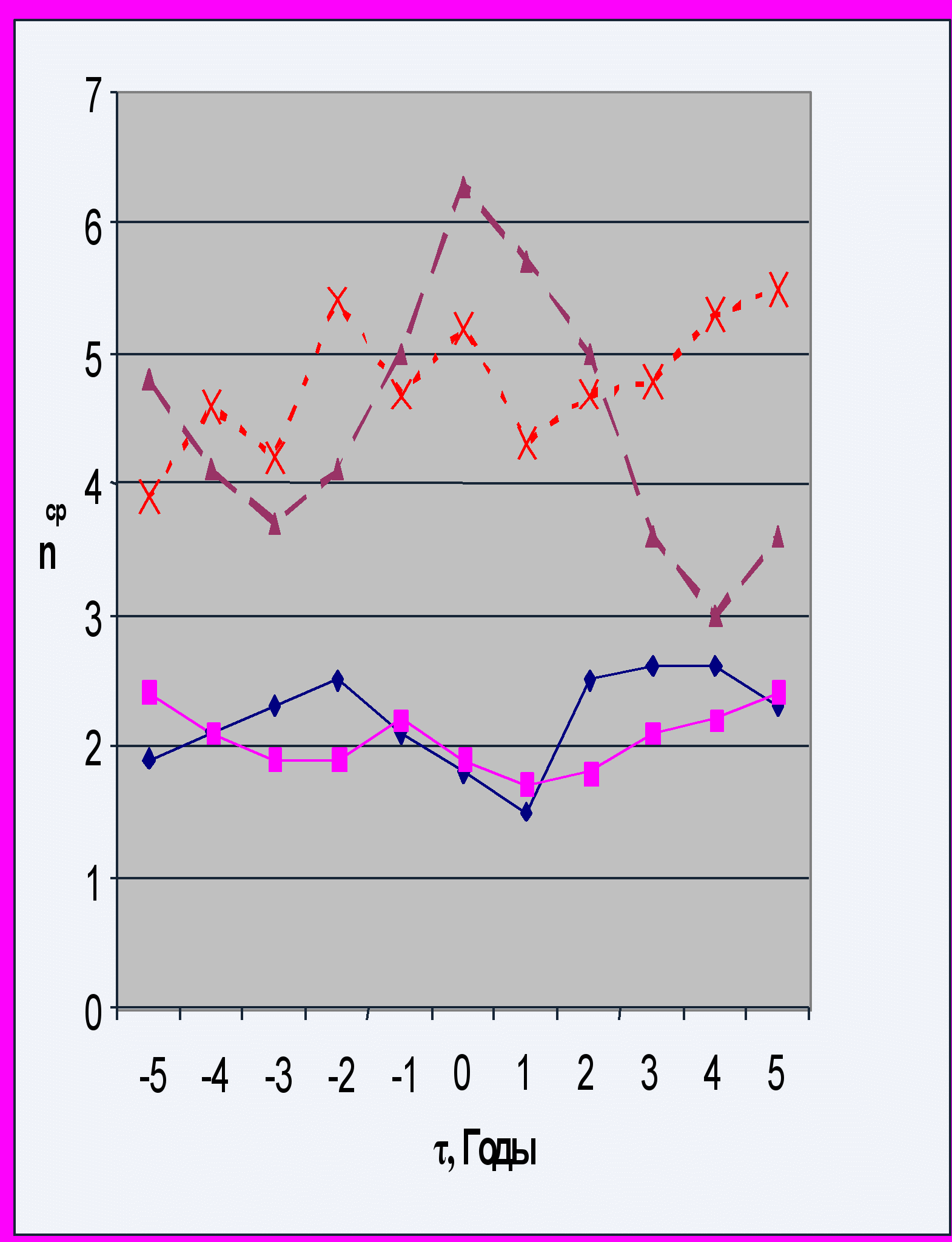
Рис.6. Распределение числа болидов в зависимости от близости τ к году максимальной СА.
1 – четные цикл 19 века, 2 ■ - нечетный цикл 19 века; 3 ▲– нечетный цикл 20 века; 4 х - четный цикл 20 века;
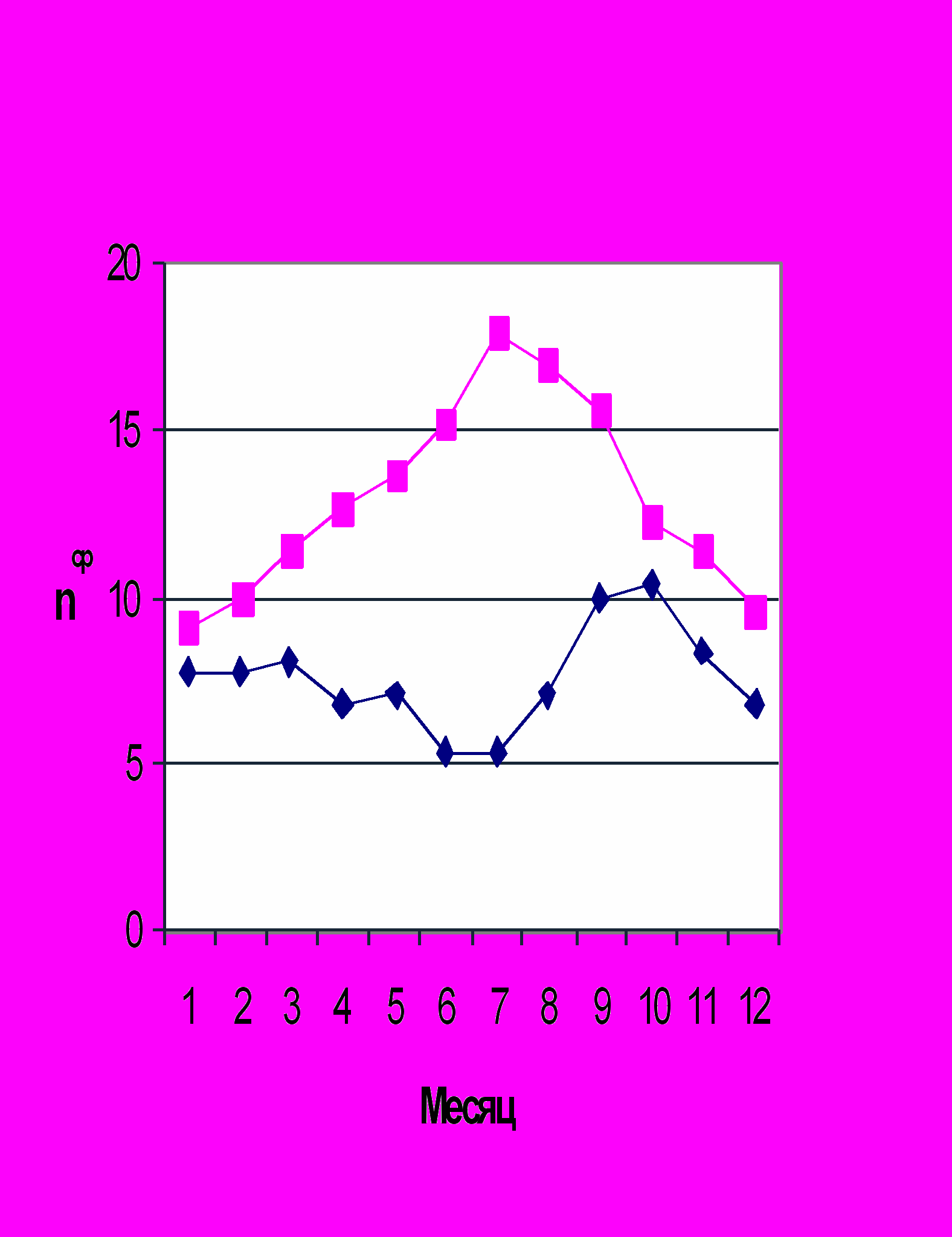
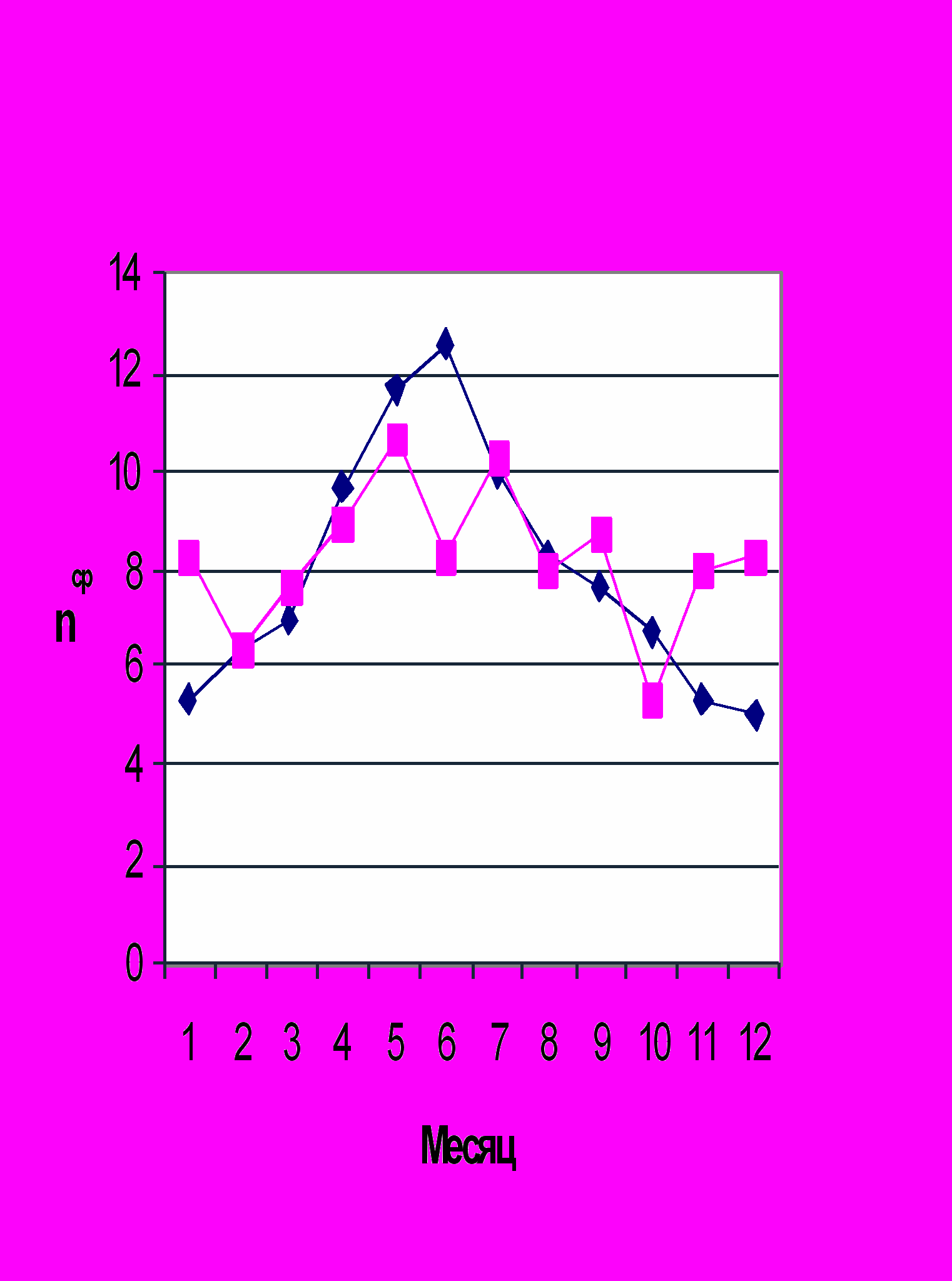
Рис.7. Годичная вариация численности болидов в четные циклы СА.
1 – в период τ4 - n = 90;
τ4 – четыре ближайших года к максимальной СА.
2 ■– в остальные 7 лет четного цикла, n = 156.
Рис.8. Годичная вариация болидов в нечетные циклы СА.
1 – в период τ4 - n = 95
2 ■– в остальные 7 лет нечетных циклов СА, n = 99.
Оказалось, что в 20 веке в нечетные циклы СА максимальное число болидов совпадает с максимальной солнечной активностью ТСА ( рис. 4, кривая 1 ; рис. 6, кривая 3). В 19 веке к значению ТСА ближе минимальное число болидов (рис.6, кривые 1 и 2). Такое же распределение болидов в 19 веке отметил и В. А. Алексеев [7].
Автором данной статьи было обнаружено еще одно различие числа болидов в четные и нечетные циклы СА, а именно, в годичной вариации численности болидов (рис. 7 и 8). В четные циклы СА в 4 года, близкие к максимальной СА (τ4) число болидов максимально зимой и минимально летом (рис. 7, кривая 1 и рис.9, кривая 1). В остальные 7 лет четных циклов и во все годы нечетного цикла максимальное число болидов приходится на лето. Если же определяется годичная вариация без учета этих особенностей, то в среднем получается (как показано на рис. 8) максимальное число болидов летом и минимальное – зимой, что как раз и получается у других авторов [7,10]. Бабаджанов П.Б. [10] объясняет: ”увеличение численности метеоров в мае-июле оказалось связанным с тем фактом, что именно в этот период орбиту Земли пересекает значительно большее количество комет, чем в остальное время года”. По мнению Алексеева В.А. [7] увеличение числа болидов летом можно отнести к “социальному фактору”, так как обычно зимой люди меньше замечают небесные явления. Оба автора не совсем правы. Число болидов зависит не только от цикла солнечной активности, но и от близости года регистрации болида к максимальной солнечной активности ТСА ( рис. 6, 7 и 8). Кроме того, имеется зависимость и от сезона года. Когда на северном полушарии лето, и небо почти круглые сутки светлое, замечаются только болиды значительно ярче Венеры, а зимой – наоборот, часов 16 можно наблюдать любые болиды. На рис.9 показано как зависит от δ годичная вариация численности болидов в четный цикл СА. На экваторе (для
 < 10˚) число болидов не зависит от знака δ. Кривые совпадают.
< 10˚) число болидов не зависит от знака δ. Кривые совпадают.Таким образом, число болидов зависит от цикла СА и от года в цикле, но все же общим является увеличение числа болидов в годы близкие к максимальной солнечной активности, особенно, в нечетные циклы. В годы максимальной СА метеоритная опасность для космических аппаратов в несколько раз больше, чем в годы спокойного Солнца. Подтверждением всего выше изложенного могло бы служить “групповое” расположение вспышек на Солнце, различное для четного и нечетного циклов СА (различные гелиоцентрические долготы) в 4 года (τ4) ближайших к году максимальной СА.

Рис. 9. Годичная вариация численности болидов [11] со склонениями
 >10˚., четный цикл.
>10˚., четный цикл.  1 - δ > 10˚, n1 = 144 (северное полушарие) ;
1 - δ > 10˚, n1 = 144 (северное полушарие) ;  2 - δ < -10˚, n2 = 44 (южное полушарие).
2 - δ < -10˚, n2 = 44 (южное полушарие).Два замечания:
1). Когда метеорные тела летят от определенного узла орбиты Меро, должна существовать годовая волна СА, так как короткоживущие явления СА на обратной стороне Солнца с Земли не видны. Автором действительно получена годовая волна по данным Блажко С.Н. [4], а вот двухлетних периодов с 1900 по 1928 год не оказалось.
2). В табл.2 последняя дата максимальной СА указана 1979,5. Следующая дата должна быть около 1990 г. (22й цикл). В книге Коротцева О.Н. [6] амплитуда чисел Вольфа для этого цикла равна 155W (одна из наибольших), а все четыре значения ∆i показали отсутствие сближений Меро с Юпитером и Сатурном. Это примерно такая же ситуация, какая была в 1770 году, после чего изменился период Меро. Вот и теперь дата -1990 г.- является исключением. Возможно, что между Юпитером и Сатурном имеются какие-то массивные тела. Например, была комета Шумейкеров-Леви 9, которая в 1994 г. упала на Юпитер [6]. Это можно проверить, если построить график распределения по афелию болидов в 22ом цикле СА и сравнить этот график с графиком распределения болидов по афелию в среднем за последние 300 лет из каталога Терентьевой А.К.[12]. Такое сравнение за 20й цикл четко показало, что болиды в 20ом цикле летели от Юпитера, а от Сатурна их не было.
Вывод .
Можно утверждать, что связь солнечной активности с орбитами Юпитера и Сатурна существует. Связующим звеном является рой метеорных тел Меро, орбита которого находится между Юпитером и Сатурном. После сближения Меро с этими планетами многие тела роя покидают свою орбиту и в виде облака летят во все стороны и в том числе прямо на Солнце, увеличивая его активность, и на Землю, увеличивая число наблюдений болидов.
Удивление вызывает тот факт, что сближение Меро с Юпитером и Сатурном происходит в 2 раза чаще в даты ТСА нечетных циклов и наблюдение болидов происходит в 2-3 раза чаще вблизи даты ТСА нечетных циклов, чем в четные.
Версия о существовании Меро объясняет многие явления, такие как связь ТСА с орбитами Юпитера и Сатурна, а так же увеличение числа метеоритов и болидов в годы максимальной солнечной активности.
Литература.
1.Шувалов В.М. “ Зависимость циклической солнечной активности от положения планет”. АВ, IV, №4, 1970, с.198.
2. Долгинов А.З. и др. “О корреляции активности Солнца с приливными силами”. АВ, VI, №3, 1972, с.195 .
3. Цесевич В.П. “Что и как наблюдать на небе”. М.,”Наука”, 1979, с.196.
4. Блажко С.Н. “ Курс общей астрономии”. ОГИЗ М.Л., 1947, с.285.
5. Казимирчак-Полонская Е.И. “Захват комет Юпитером ”. Астрономия и небесная механика. М.Л. 1978 . с.340, 401.
6. Коротцев О.Н. Астрономия. 2003. с.313, 515.
7.Алексеев В.А. Статистика метеорных выпадений. Метеоритика. №47,1988. с.24.
8.Зоткин И.Т. и Хотинок Т.Л. Число крупных болидов по наблюдениям за 50 лет. Метеоритика. №37, 1978. с.37.
9. Метеоритика №9, №12, №30, №35, №37, 210. 1951 – 1978 (за исключением [8].
10. Бабаджанов П.Б. Метеоры и их наблюдение. М., Наука, 1987. с.129, 130.
11. Метеоритика. №37, 1978. с.44-60.
12. Тереньева А.К. “Орбиты малых метеорных роев”. Астрономический циркуляр. №249, 1963; №264, !963; №415, 1967; №№442, 423, 1967.
