Эффекты эйнштейна и шапиро в контексте экспериметальных исследований

Вид материала

Документы

Содержание 4 Справочные материалы 4.2 Список использованных источников 4.3 Отклонение лучей S координат на некоторое произвольное расстояние R 4.4 Эффект эйнштейна 4.5 Эффект эйнштейна

Подобный материал:

• Автор(ы): Шапиро М., Год, 4188.71kb.
• А. В. Брушлинского и научного сотрудника А. З. Шапиро, 1854.41kb.
• К. В. Айгон М.: Институт Общегуманитарных Исследований. Серия. Современная психология:, 2103.15kb.
• Специальная теория относительности (сто) покоится на двух китах: оптике и механике,, 544.46kb.
• Книга содержит анализ теории относительности и творчества Эйнштейна другими великими, 174.63kb.
• Фонд перспективных исследований и инициатив, 815.29kb.
• Сс-системы и соответственно повреждающие эффекты стресс-реакции, в механизме устойчивости, 19.64kb.
• «Методология изучения диаспор: теория и практика», 62.12kb.
• Необыкновенные приключения феминизма в россии, 415.51kb.
• Любой космический комплекс несет на себе следующие эффекты: Коммерческий или финансовый, 11.44kb.

4 СПРАВОЧНЫЕ МАТЕРИАЛЫ

 

4.1 ПЕРЕЧЕНЬ ОСНОВНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

 

Список использованных источников к ссылкам настоящего перечня расположен ниже, в пункте 4.2

1. На результатах измерений сказывается отклонение от сферичности формы Солнца, составляющая /37/ 5,21 х 10^-3 %, из-за которой результаты наблюдений отклонений звезд оказываются зависимыми от углового положения радиуса - вектора звезды на небесной сфере и могут различаться в пределах 9,2 x 10^-5 ".

2. Влияние колебаний расстояния от Земли до Солнца при ее орбитальном вращении вокруг Солнца, т.е. влияние отклонения от круглости ее орбиты, составляющего 1,67 %, оценивается дополнительным отклонением звезд, достигающим 2,88 x 10^-2 ".

3. Дополнительное отклонение, обусловленное рефракцией лучей в атмосфере Солнца, достигает /38-39/ 0,004 ".

4. Значительным является вклад рефракции и дисперсии в атмосфере Земли, который зависит от высоты Солнца над горизонтом и достигает 0,01...0,1 ".

5. Атмосферная экстинкция, или дрожание изображения звезды, связанное с неоднородностью земной атмосферы, имеет амплитуду около 1 " /40/. Это явление не вызывает значительной погрешности измерения, поскольку период экстинкции составляет всего 0,1...0,2 с, тогда как время экспонирования при фотографировании достигает десятков секунд. Экстинкция приводит к "размыванию" изображения звезды около неискаженного экстинкцией ее положения. Значительные погрешности могут создавать /41/ систематические смещения большей продолжительности, распространяющиеся на целые группы звезд и вызываемые атмосферной турбулентностью /34 - 36/.

6. В модели Эйнштейна Земля и Солнце (а также закрывающая Солнце Луна) считались точечными объектами. Обладание ими ненулевыми размерами приводит к тому, что наблюдатель в общем случае располагается на некотором удалении от центральной линии. Подобное смещение вызывает погрешность отклонения звезд, достигающую /4; 42/ 2 x 10^-4 ".

7. Необходимо также учитывать, что во время затмения на отклонение луча влияют поля тяготения Луны и Земли, обусловливающие добавку к релятивистскому отклонению луча в 5,8 x 10^-4 ".

8. Добавка, зависящая от длины волны светового луча, оценивается значением 2,5 x 10^-4 ".

9. Установлена /43/ также корреляционная зависимость между индексом солнечной активности (числами Вольфа /44/) и отклонением звезд. Анализ этой зависимости позволяет считать вклад этого явления в отклонение лучей достигающим 0,156 ". Эта зависимость подтверждается также высокой теснотой корреляции /44-45/ среднегодовой гелиографической широты солнечных пятен с отклонением лучей.

10. Гипотетический эффект Курвуазье /3/ (непараллактическое годичное смещение видимых положений звезд) достигает в максимуме (на расстояниях около восьми солнечных радиусов) значений 1 ". При меньших угловых удалениях звезд от Солнца, т.е. в области оптических наблюдений эффекта Эйнштейна наблюдается уменьшение этого эффекта. Данное явление может по-видимому вносить наиболее существенный вклад в суммарную погрешность, хотя, с другой стороны, авторы /46-47/ считают этот эффект весьма сомнительным, либо целиком объясняют инструментальными и физиологическими ошибками, допущенными при его обнаружении.

11. Следует также упомянуть /3; 34-36; 48-52/ аддитивную погрешность от несовпадения масштабов дневного и ночного снимков, достигающую 0,25 " и частично компенсируемую поправкой; погрешность, вызванную неточностью наложения фотографий; погрешности, связанные с влиянием изменений температуры воздуха в ходе затмения на измерительную аппаратуру, с короблением фотопластинки и др. Кроме того, на результатах измерений сказываются преломление лучей в атмосфере Солнца; аномальное преломление в земной атмосфере, находящейся в конусе лунной тени; гипотетическое влияние электрического заряда Солнца, его плазменных потоков и т.п.

 

4.2 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

К ПЕРЕЧНЮ ПОГРЕШНОСТЕЙ

 

3. Вавилов С.И. Экспериментальные основания теории относительности // Новейшие течения научной мысли.- Вып. 3/4.-М.,-Л., Государственное изд-во, 1928.-172 с.

4. Гравитация: [В 3-х т.] / Ч.-В.Мизнер, К.Торн, Дж.Уиллер; Пер. с англ. М.М.Баско; Под ред. В.В.Брагинского и И.Д.Новикова.М., Мир, 1977.

34. Ацюковский В.А. Логические и экспериментальные основы теории относительности. М., изд-во МПИ, 1990.-55 с.

35. Ацюковский В.А. Общая эфиродинамика. Моделирование структур вещества и полей на основе представлений о газоподобном эфире.-М.: Энергоатомиздат, 1990.-280 с.

36. Ацюковский В.А. Материализм и релятивизм. Критика методологии современной теоретической физики.-М.: Инженер, 1993.-192 с.

37. Dicke // Ann. Rev. Astron. Ap.-1970.-N 8.-P. 297.

38. Арифов Л.Я., Кадыев Р.К. // Новейшие проблемы гравитации: Тезисы докл. / Всесоюзн. симпозиум.-М., 1968.

39. Бронштэн В.А. Об эффекте Эйнштейна и рефракции в Солнечной короне // Поле и материя. Сборник статей по физике и геофизике, посвящ. памяти проф. К.А.Путилова [Отв. ред. Я.П.Терлецкий].-М.: Изд-во Моск. ун-та, 1971.

40. Боков А.Д. // Астрономический циркуляр.-1966.-N 356.

41. Нестеров В.В., Подобед В.В. Общая астрометрия.-М.: Наука.-1982.

42. Лайман А., Пресс В., Прайс А., Тюкальс С. Сборник задач по теории относительности и гравитации.

43. Костин Б.В. // Астрономический циркуляр.-1965.-N 334.

44. Бакунин П.И., Кононович Э.В., Мороз В.И. Курс общей астрономии.-М.: Наука.-1974.-С.295.

45. Курт В.Г. Исследование космического пространства с помощью ИСЗ и АМС // Развитие астрономии в СССР.-М.:Наука, 1967.

46. Kienle H. // Phys. Z.-Bd. 25.-S.1

47. Kopff // Phys. Z.-Bd. 25.-S. 95.

48. Митенок В.В. // Проблемы теории гравитации и элементарных частиц.-М.: Атомиздат, 1977.-Вып. 8.-С. 156.

49. Ушаков Е.А., Костюкевич Н.Н. // Изв. АН БССР.- Сер. физ.-мат. науки.-1976.-N 3.-С. 113.

50. Ушаков Е.А., Костюкевич Н.Н. // Изв. АН БССР.- Сер. физ.-мат. науки.-1976.-N 6.-С. 242.

51. Jeffery G.B. // Proc. Roy. Soc. A.-1929.-V. 99.-P. 123.

52. Detre L. // Ann. Univ. Sci. Budapest, sect. geol.-1963.-Vol. 7.-PP. 99-108.

  

4.3 ОТКЛОНЕНИЕ ЛУЧЕЙ

В ТЕОРИИ ВСЕМИРНОГО ТЯГОТЕНИЯ

 

Для количественной оценки угла  по Зольднеру воспользуемся прямоугольной декартовой системой координат, в начале которой располагается тяготеющая масса - Солнце S (рис.1.2).



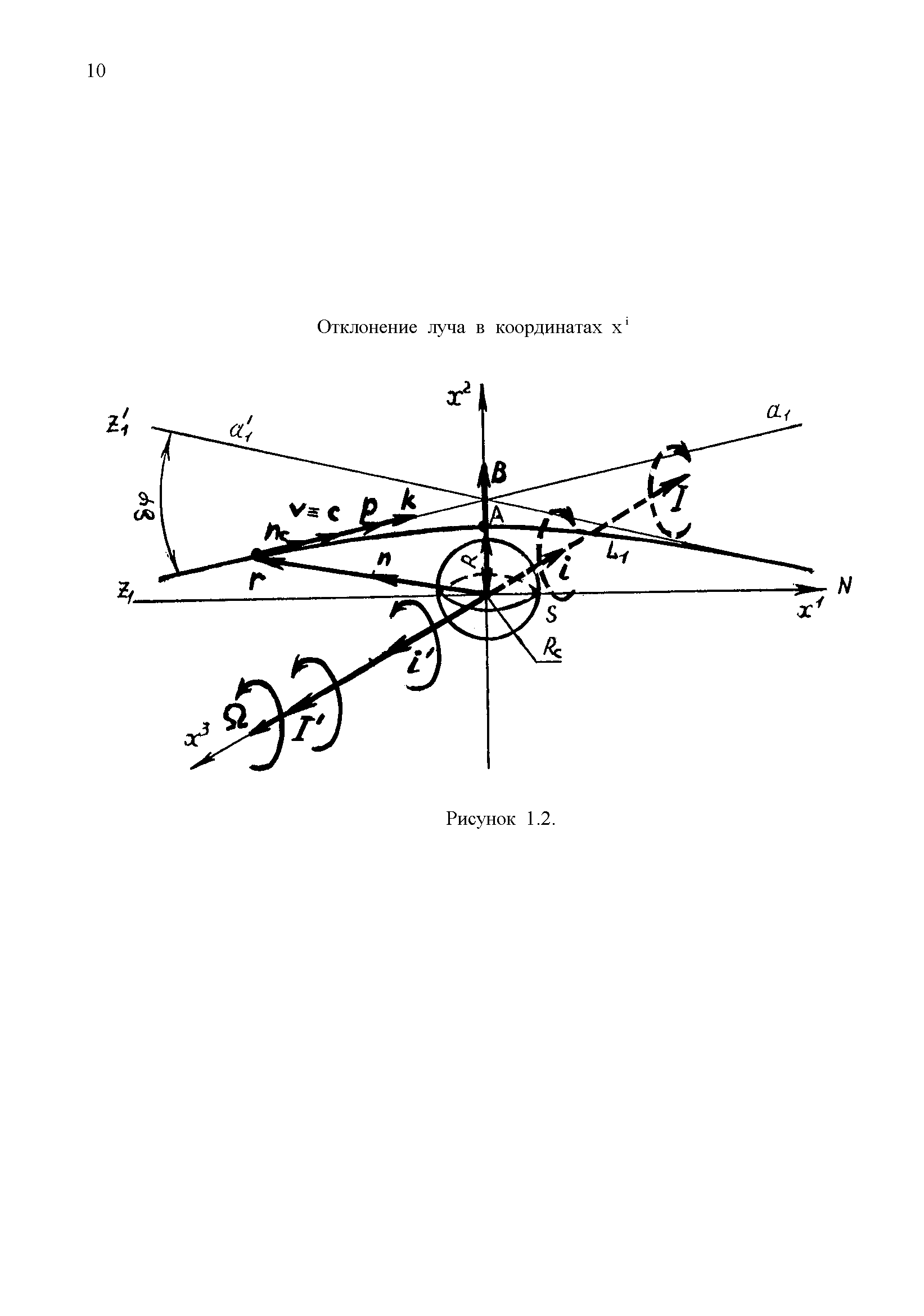
Пусть световой луч удален от начала S координат на некоторое произвольное расстояние R, которое определяется лежащей на луче точкой А. Проведем координатную ось х¹ в направлении, перпендикулярном вектору SA, таким образом, чтобы перемещение световой корпускулы вдоль луча сопровождалось возрастанием координаты х¹. Координатная ось х² направлена при этом в сторону SA.

Будем также считать бесконечно удаленного наблюдателя N неподвижным относительно назначенной таким образом системы координат.

Искомый угол   , согласно данному выше определению, равен разности углов

(1.1)

наклона к оси х¹ прямых, касательных к лучу в бесконечно удаленных от начала координат точках х¹ =   оси х¹, каковыми согласно рис.1.1 являются асимптоты а₁ и а₁'. Вследствие малости угла  можно приравнять функцию тангенс ее аргументу:

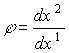(1.2)

и записать

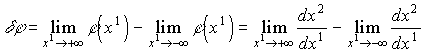. (1.3)

Разность  следует брать со знаком "минус" при отклонении лучей в сторону центра Солнца. В противном случае величина  должна была бы быть положительной.

Согласно второму закону И.Ньютона на световую корпускулу со стороны Солнца действует вектор силы

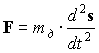, (1.4)

где ds - вектор элементарного перемещения световой корпускулы; m_д - ее масса движения. В условиях неопределенности понятия массы применительно к фотону заметим, что для дальнейшего анализа следует лишь иметь в виду обладание фотоном ненулевой массой движения (m_{д } 0).

Введем временную координату х⁰ = сt. Пусть начальному моменту времени t = x⁰ = 0 соответствует положение световой корпускулы в точке А. Как будет показано ниже, значения угла  достаточно малы для того, чтобы с хорошим приближением считать световой луч прямой x²=SA , параллельной оси х¹.

По этой причине можно приравнять

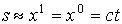. (1.5)

Скорость света с является постоянной по значению величиной. Следовательно, вектор ускорения световой корпускулы d²s/dt², как и вектор силы F (1.4), не содержат составляющей, направленной вдоль траектории движения корпускулы, т.е. направлены перпендикулярно световому лучу. Поэтому будем считать, что вектор силы F (1.4) направлен перпендикулярно оси х¹, т.е. вдоль х². Кроме того, вместо производной d²s/dt² в (1.4) следует использовать производную d² (x²)/dt²:

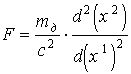. (1.6)

С другой стороны, в соответствии с законом всемирного тяготения модуль силы F составляет:

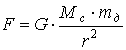, (1.7)

где G - гравитационная постоянная; M_с - масса Солнца; r² - квадрат текущего расстояния между световой корпускулой и Солнцем, с учетом (1.5) равный:

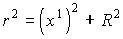. (1.8)

Приравнивая (1.6) и (1.7) с учетом (1.8) и деля обе части получившегося равенства на m_д  0, имеем:

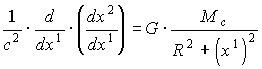. (1.9)

Интегрируя (1.9) в пределах от х¹ = -  до х¹ = +  , как того требует (1.3), получаем:

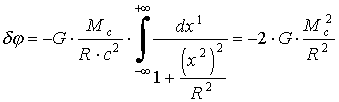. (1.10)

Знак "минус" в правой части (1.10) назначен для того, чтобы подчеркнуть направление отклонения светового луча в сторону начала координат. Введем обозначения:

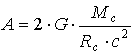; (1.11)

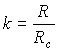. (1.12)

где R_c - солнечный радиус, и, следовательно, k - есть расстояние наибольшего сближения луча с Солнцем. Тогда, с учетом (1.11) - (1.12), выражение (1.10) преобразуется к виду:

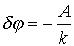. (1.13)

Подставляя в правую часть равенства (1.10) числовые значения входящих в него физических величин G=6,6710^-11 Н м^2 кг^-2 ; M_с=1,9910³⁰ кг; с=310⁸ м с^-1; R_с=6,9610⁸ м, получаем значение постоянной А, равное 4,24  10^-6. При k = 1, что согласно (1.12) соответствует касанию Солнца лучом, в выражении (1.10) угол   равен "минус" A, и, таким образом, величина A есть абсолютное значение угла   отклонения луча в случае касания им Солнца, причем его значение исчислено в радианах. Переводя значение А в угловые секунды, вслед за Зольднером имеем: А = 0,87 ".

 

4.4 ЭФФЕКТ ЭЙНШТЕЙНА

КАК ОТКЛОНЕНИЕ ОТ ПРЯМОЛИНЕЙНОСТИ

ТРАЕКТОРИИ РАСПРОСТРАНЕНИЯ

ВОЛНОВОГО 4-ВЕКТОРА

 

В геометрической оптике лучом считается линия, касательные к которой в каждой точке совпадают с направлением распространения волны электромагнитного излучения. Если f есть некоторая величина, описывающая поле волны и характеризующаяся амплитудой а, частотой  и начальной фазой  , то для плоской монохроматической волны можно записать:

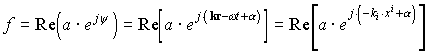. (1.14)

 где величина k называется волновым 4-вектором:

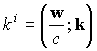; (1.15)

j - мнимая единица; индекс i, а также индексы, использованные ниже и обозначенные буквами j; k; l; и s латинского алфавита, могут принимать значения 0; 1; 2; 3. Здесь и далее по повторяющимся индексам производится суммирование в соответствии с правилами тензорной алгебры.

Величина  носит название эйконала. Эйконал, согласно (1.14) описывает поведение волнового процесса в пространстве и во времени. В окрестностях Солнца, в пределах расстояний, соизмеримых с солнечным радиусом, т.е. значительно превосходящих длины волн излучения звезд и существенно меньших межзвездных расстояний, излучение звезд можно считать плоскими волнами. Поэтому для определения отклонения лучей необходимо исследовать поведение эйконала в гравитационном поле Солнца с учетом релятивистских эффектов.

Анализируя (1.14) - (1.15), запишем, что

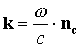. (1.16)

где n_с - единичный вектор в направлении распространения волны. Кроме того:

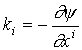. (1.17)

Сравнивая (1.15) и (1.16), можно установить, что квадрат волнового 4-вектора равен нулю:

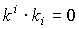. (1.18)

 Подставляя (1.17) в (1.18), получаем уравнение эйконала:

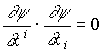. (1.19)

 Проанализируем поведение эйконала в гравитационном поле. Перепишем (1.19) в контравариантных компонентах

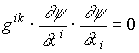. (1.20)

где g^ik - компоненты метрического тензора, соответствующего, согласно выводам теории относительности, метрике Шварцшильда, которая в сферических пространственных координатами r;  ;  имеет вид:

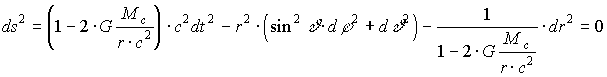. (1.21)

Поле тяготения, соответствующее метрике (1.21) является центрально - симметричным, поэтому световые лучи представляют собой плоские кривые. Если движение происходит в плоскости =/2, то d=0 и sin=0, а следовательно:

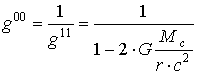; (1.22)

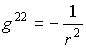; (1.23)

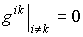. (1.24)

Подставляя (1.22) - (1.24) в (1.20), имеем:

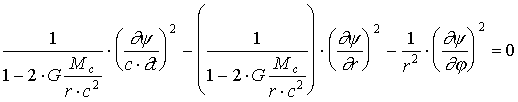. (1.25)

Выражение (1.20) по своей структуре отличается от уравнения Гамильтона - Якоби

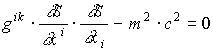. (1.26)

соответствующего движению частицы массой m, где S - действие, лишь на вычитаемое m²c². Поэтому, решение (1.20) находится по общим правилам решения уравнения Гамильтона - Якоби в виде:

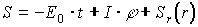, (1.27)

с той лишь разницей, что вместо действия S определяется эйконал , и следовательно, радиальной части действия S_r(r) в искомом решении соответствует радиальная часть эйконала _r(r), а постоянным коэффициентам - энергии E₀=-S/t и моменту импульса I=S/ частицы соответствуют частота ₀=-/t электромагнитного излучения и константа / :

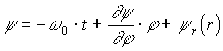. (1.28)

Заметим, что величина

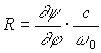(1.29)

имеет размерность расстояния. Подстановкой (1.28) в (1.25) с введением обозначения (1.29) можно определить радиальную часть _r(r) эйконала:

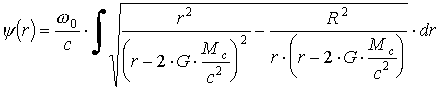. (1.30)

Заменяя в (1.30) переменную интегрирования

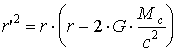, (1.31)

пренебрегая в сравнении с r' членом G^{2 } M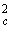/c⁴: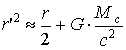

(1.32)

а далее - членом 2 r' G M_c / с²:

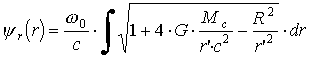(1.33)

и раскладывая (1.33) в ряд Маклорена по степеням второго слагаемого под знаком радикала с последующим интегрированием, получаем:



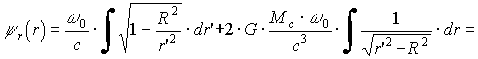
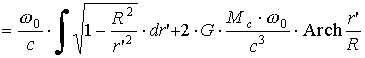. (1.34)

Форма светового луча согласно (1.28) определяется производной =d[_r(r)]/d[/], или, с учетом (1.29), =[_r(r)]/[R₀/c]=(c/₀){[_r(r)]/R}:



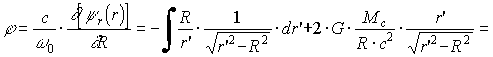
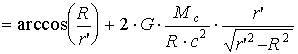. (1.35)

Первое слагаемое в (1.35) определяет прямую линию r'=R/cos , проходящую на расстоянии R от начала координат и соответствующую прямолинейному световому лучу, каким его можно считать ввиду малости анализируемого явления. Второе слагаемое представляет собой поправку к положению луча, которая согласно (1.1) - (1.3) позволяет вычислить искомое отклонение  луча, как взятую с отрицательным знаком разность ее пределов при изменении r' в пределах от - до + . Это отклонение составляет:

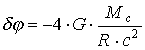. (1.35a)

Выделяя в (1.35a) величину k (1.12) и сравнивая получающееся выражение с (1.13), убеждаемся, что абсолютное значение A отклонения луча, касающегося края Солнца, вычисляется по формуле

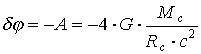(1.36)

и превосходит в два раза аналогичное значение (1.11), рассчитанное Зольднером, составляя при этом 1,75 ".

Двукратное увеличение отклонения обусловлено кривизной околосолнечного пространства - времени, которая учитывается метрикой (1.21).

 

4.5 ЭФФЕКТ ЭЙНШТЕЙНА

КАК ОТКЛОНЕНИЕ ОТ ПРЯМОЛИНЕЙНОСТИ

ТРАЕКТОРИИ ДВИЖЕНИЯ

4-ИМПУЛЬСА ЧАСТИЦЫ

 

В литературных источниках можно обнаружить также расчет отклонения светового луча, исходя из корпускулярных представлений. Световая корпускула при этом движется вдоль геодезической линии пространства - времени, являющимся пространством Римана, уравнение которой имеет вид:

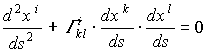, (1.39)

где xⁱ - система координат, пространственные компоненты которой соответствуют рассмотренному выше (см. рис.1.2) зольднеровскому анализу отклонения; Г 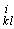- символы Кристоффеля:

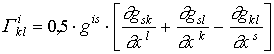, (1.40)

а g^is - компоненты метрического тензора.

Геометрия пространства - времени в окрестностях считающегося неподвижным Солнца при этом соответствует упрощенной метрике Шварцшильда (1.21), переписанной в декартовых координатах:

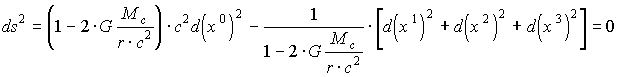. (1.41)

Возведенным в отрицательную степень множимым вычитаемого (1.41) пользоваться далее неудобно. Его следует разложить в ряд:

 

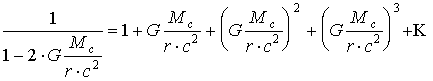, (1.42)

а для подстановки в (1.41) ограничиться первыми двумя членами ряда

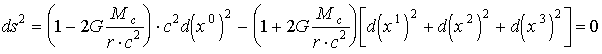. (1.43)

При этом, компоненты метрического тензора составляют:

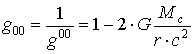; (1.44)

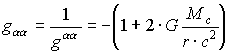; (1.45)

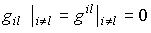, (1.46)

где индекс  пробегает значения 1; 2; 3.

В силу (1.5), имеем:

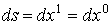, (1.47)

а следовательно, выражение (1.39) преобразуется к виду:

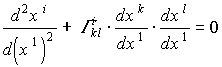. (1.48)

Искомое отклонение  (1.3) определяется как разность производных  (1.2), благодаря чему можно записать:

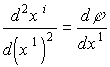, (1.49)

после чего искать  и   подстановкой (1.48) в (1.49) при i = 2:

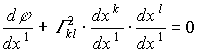. (1.50)

Для подстановки в (1.50) символов Кристоффеля воспользуемся формулой (1.40) с учетом (1.44) - (1.46) и (1.42):

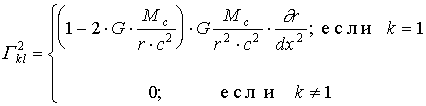. (1.51)

Так как величина А (1.11) существенно меньше единицы, а входящее в (1.51) вычитаемое из заключенной в круглые скобки разности меньше А в R_c/r раз, где rR_c, то подобным вычитаемым можно пренебречь в сравнении с уменьшаемым - единицей. Кроме того, дифференцируя (1.8) с учетом x²=R:

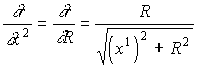(1.52)

с последующим использованием в (1.51), имеем:

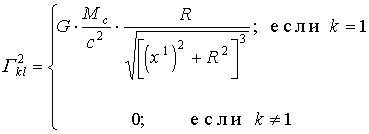. (1.53)

Так как отклонение луча от горизонтали является пренебрежимо малым: х²=