Учебно-методический комплекс по дисциплине Специальность 033100 Физическая культура (очное отделение, срок обучения 5 лет)
| Вид материала | Учебно-методический комплекс |
СодержаниеЦель работы. Порядок выполнения работы Лабораторная работа №3. Оценивание с использованием стандартных шкал Разновидности шкал. Стандартные шкалы Шкалы выбранных точек Шкала ГЦОЛИФК. Цель работы |
- Учебно-методический комплекс по дисциплине Специальность 033100 (050720) «Физическая, 225.94kb.
- Учебно-методический комплекс по дисциплине Специальность 033100 (050720) «Физическая, 343.13kb.
- Учебно-методический комплекс по дисциплине Специальность 033100 (050720) «Физическая, 1063.84kb.
- Учебно-методический комплекс по дисциплине Специальность по гос впо (050720) «Физическая, 513.83kb.
- Учебно-методический комплекс дисциплины специальность 033100 (050720) «Физическая культура», 243.87kb.
- Учебно-методический комплекс по дисциплине Специальность 033100 (050720) «Физическая, 154.92kb.
- Учебно-методический комплекс по дисциплине Специальность 050720 (033100) Физическая, 516.63kb.
- Учебно-методический комплекс дисциплины/ Специальность 033100 (050720)- «Физическая, 219.1kb.
- Курс очное отделение (п олный срок обучения) 4 курс очное отделение (сокращенный срок, 18.56kb.
- Учебно-методический комплекс дисциплины Специальности 033100 (050720) Физическая культура, 606.13kb.
Лабораторная работа №2. Расчет сопоставительных норм оценок
 Цель работы. Ознакомление с методами расчёта норм оценок на основе результатов тестирования.
Цель работы. Ознакомление с методами расчёта норм оценок на основе результатов тестирования.Краткие теоретические сведения. Показанные спортсменами результаты (в тестах):
- выражаются в разных единицах измерения и, поэтому несопоставимы друг с другом;
- Сами по себе не указывают, насколько удовлетворительно состояние спортсмена (12,0 в беге на 100 м - это хорошо или плохо?., и для кого?).
По этим причинам результаты тестов принято переводить в оценки (очки, баллы, разряды и т.д.).
Оценкой называется унифицированная мера успеха в каком-либо задании, в частном случае - в тесте.
Например: разряды ЕВСК, таблицы очков по видам спорта, школьные, вузовские отметки (отл-хор-удовл-неуд, зачёт-незачёт, "1"-"5").
Нормой в спортивной метрологии называется граничная величина результата теста, на основе которой производится классификация спортсменов.
Существует три вида норм: сопоставительные, индивидуальные и должные. Сопоставительные нормы устанавливаются после сравнения достижений людей, принадлежащих к одной и той же группе (совокупности) в следующем порядке:
- выбирается совокупность людей;
- измеряются их достижения в комплексе тестов;
- основой для расчёта норм является функция нормального распределения (имеющая симметричную колоколообразную форму). Поэтому определяются средние величины и стандартные отклонения;
Если классифицировать нормы оценок по 5-балльной шкале, они будут выглядеть так:
Оценка "3" - от Xср до Хср+σ
Оценка "4" - от Хср+σ до Хср+2σ
Оценка"5" - отХср+2σ до Хср+Зσ
Классификация оценок может быть основана на 7-балльной шкале:
Очень низкая - <Хср-2σ
Низкая - от Хср-2σ до Хср-1σ
Ниже средней - от Хср-1σ до Хср-0,5σ
Средняя - от Хср-0,5σ до Хср+0,5σ
Выше средней - от Хср+0,5σ до Хср+1σ
Высокая - от Хср+1σ до Хср+2σ
Очень высокая - >Хср+2σ
Порядок выполнения работы:
- Перерисовать таблицу расчёта оценочных норм в тетрадь.
| Объём выборки, n | Значения выборки, xi |
| 1 | |
| 2 и т.д. | |
- Во второй столбец таблицы занести исходные значения выборки, на основе которых будет производиться расчёт оценочных норм.
- Значения выборки записываются в отдельные столбики, и определяется количество значений (объём) выборки - n;
- Определяется среднее арифметическое выборки - Хср;
- Определяется коэффициент ряда нормального распределения - k по таблице, представленной ниже (значение коэффициента находится по объёму выборки - n):
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | - | - | 1,128 | 1,692 | 2,058 | 2,325 | 2,534 | 2,704 | 2,847 | 2,970 |
| 10 | 3,077 | 3,171 | 3,258 | 3,335 | 3,406 | 3,531 | 3,587 | 3,587 | 3,640 | 3,688 |
| 20 | 3,734 | 3,778 | 3,819 | 3,858 | 3,895 | 3,930 | 3,964 | 3,996 | 4,027 | 4,057 |
| 30 | 4,085 | 4,112 | 4,139 | 4,164 | 4,180 | 4,213 | 4,236 | 4,258 | 4,280 | 4,307 |
| 40 | 4,321 | 4,341 | 4,360 | 4,379 | 4,397 | 4,415 | 4,432 | 4,449 | 4,456 | 4,482 |
| 50 | 4,498 | 4,513 | 4,528 | 4,543 | 4,557 | 4,571 | 4,585 | 4,599 | 4,612 | 4,625 |
| 60 | 4,638 | 4,651 | 4,663 | 4,675 | 4,687 | 4,699 | 4,710 | 4,721 | 4,733 | 4,743 |
| 70 | 4,754 | 4,765 | 4,775 | 4,785 | 4,796 | 4,805 | 4,815 | 4,825 | 4,834 | 4,844 |
| 80 | 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 |
| 90 | 4,94 | 4,95 | 4,96 | 4,96 | 4,97 | 4,98 | 4,98 | 4,99 | 5,00 | 5,01 |
| n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| | 5,02 | 5,49 | 5,76 | 5,94 | 6,07 | 6,18 | 6,28 | 6,35 | 6,42 | 6,48 |
- Определяется разница между наибольшим и наименьшим значениями выборки - х;
- Определяется стандартное отклонение выборки по формуле:
| σ = | х |
| k |
- На основе имеющихся значений среднего арифметического и стандартного отклонения рассчитать нормы оценок по 5-балльной и 7-балльной шкалам.
Лабораторная работа №3. Оценивание с использованием стандартных шкал
Краткие сведения по теории оценок и норм. Показанные спортсменами результаты (в частности, результаты тестов) во-первых, выражаются в разных единицах измерения (время, расстояние и т.п.) и поэтому непосредственно не сопоставимы друг с другом. Во-вторых, сами по себе не указывают, насколько удовлетворительно состояние спортсмена (скажем, время бега не 100 м, равное 12,0 с, может рассматриваться и как очень хорошее, и как очень плохое, в зависимости от того, о чем идет речь). Поэтому результаты превращаются в оценки (очки, баллы, отметки, разряды и т.п.).
Непосредственно сопоставлять достижения в разных заданиях нельзя (скажем, не ясно, что труднее - бег 100 м за 11,0 с или прыжок в высоту на 2,00 м). В таких случаях используют косвенные подходы, в частности перевод результатов в баллы или очки на основе шкал оценок.
Разновидности шкал. Все шкалы можно разделить на две группы: пропорциональные (линейные) шкалы; нелинейные шкалы. Принято выделять четыре основных типа шкал оценок: пропорциональная шкала, регрессирующая, прогрессирующая, сигмовидная.
Стандартные шкалы относятся к группе пропорциональных шкал. Названы они стандартными потому, что масштабом в них служат стандартные отклонения. Наиболее популярна среди стандартных шкал Т-шкала. Здесь средняя величина приравнивается к 50 очкам, а стандарт - к 10 очкам, и расчет суммы баллов ведется по формуле:

Например, если средняя величина в прыжках в длину с места равнялась 224 см, а стандартное отклонение составило ± 20 см, то за результат 222 см начисляется 49 очков:
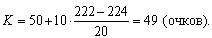
При массовых обследованиях спортсменов или групп здоровья можно использовать так называемую С-шкалу, описываемую формулой:
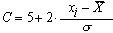
Достоинством этой шкалы является простота подсчетов, что достигается за счет меньшей точности.
Перцентильная шкала основана на мере преимущества каждого спортсмена по сравнению с более слабыми участниками соревнования. Если, например, проводится кросс с общим стартом, спортсмену можно начислять столько очков, сколько участников (в процентах) он обогнал. Если спортсмен опередил всех участников (99%), то он получает 99 очков, если опередил 72% - 72 очка и т.д. Тот же принцип можно использовать и в других тестах: число начисляемых очков приравнивается к проценту лиц, которых опередил (по результату) данный участник. Шкала, построенная таким образом, называется перцентильной, а интервал этой шкалы - перцентилем. Один перцентиль включает 1% всех испытуемых.
Шкалы выбранных точек. Описанные шкалы можно построить, если известно статистическое распределение результатов теста: средняя, стандарты и другие параметры распределения. Такие данные не всегда удается получить. Это достижимо при использовании шкалы выбранных точек. В этом случае обычно поступают так: берут какой-нибудь высокий спортивный результат (например, мировой рекорд или 10-й результат в истории данного вида спорта) и приравнивают его, скажем, к 1000 очкам. Затем на основе результатов массовых испытаний определяют среднее достижение группы слабо подготовленных лиц и приравнивают его, скажем, к 100 очкам. После этого, если используется пропорциональная шкала, остается выполнить лишь арифметические вычисления - ведь две точки однозначно определяют прямую линию.
Д

ля примера рассмотрим построение шкалы выбранных точек на основе данных мирового табеля о рангах спортсменов по итогам выступления в течение года. В нем мировым рекордам во всех видах спорта дается наивысшая сумма баллов — 1000 очков, а худшие результаты оцениваются 100 очками. Используя принцип построения пропорциональных шкал, строится график шкалы выбранных точек, представленный на рисунке. Конечный вид уравнения прямой для расчета оценок по шкале выбранных точек имеет вид:
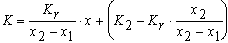

Например, лучший результат в беге на 100 м в группе исследуемых спортсменов, равный 11,0 с, оценивался 100 очками, а худший (14,0 с) — 10 очками. Тогда сумма очков спортсмена, показавшего время забега, равное 12,5 с, по формуле уравнения прямой для расчета оценок по шкале выбранных точек равна:

Шкала ГЦОЛИФК. При периодических обследованиях состав и общая численность тестируемой команды по разным причинам не остаются постоянными: кто-то заболел, кто-то отозван для участия в других соревнованиях и т.п.
Предположим, что в ноябре тестирование проводилось на 10, а в феврале на 20 спортсменах. Конечно, занять 10 место при 10 или при 20 участниках - не одно и то же (во втором случае спортсмен опередил девятерых, а в первом - никого). Кроме того, ранговая шкала (шкала порядка), например, перцентильная, неудобна тем, что она однозначно не определяет интервалы между исследуемыми.
Для случаев, когда условия тестирования не остаются постоянными, в ГЦОЛИФКе была разработана шкала, в основе которой лежит следующее математическое выражение:

где: К — оценка результата в баллах или очках.
Например, лучший результат в ударе ногой по мячу на дальность (в метрах) для подростков 10-11 лет равнялся 30,5м, худший — 8,5м. Очки, начисляемые спортсмену за результат 19,5м, рассчитываются по следующей формуле:
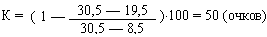
Спортсмен, показавший лучший результат, по шкале ГЦОЛИФКа всегда получает 100 очков, занявший же последнее место очков не получает.
Шкала ГЦОЛИФК относится к сигмовидным шкалам оценок, в то время как стандартные, перцентильные и шкалы выбранных точек — это пропорциональные шкалы.
Цель работы: научиться правильно выбирать шкалы оценок для оценивания результатов спортсменов в различных видах спорта.
Ход работы
- Используя данные тестирования студентов группы в показателях
xi — результаты _____________________________________
yi — результаты______________________________________
zi — результаты______________________________________
определить личный результат в баллах по каждому из предлагаемых тестов, применив следующие шкалы оценок: 1 - перцентильная шкала; 2 - шкала выбранных точек; 3 - стандартная Т-шкала; 4 - шкала ГЦОЛИФК.
- Занести результаты тестирования в рабочую таблицу 1.
- Рассчитать количество баллов, используя шкалы оценок.
Перцентильная шкала оценок
- Проранжировать показатели тестов.
- Рассчитать оценки в каждом тесте по формуле:
-

Кх = Ку = Кz =
- Распределить места по сумме очков в рабочей таблице 1 для каждого теста.
Шкала выбранных точек
- Рассчитать оценки в каждом тесте по формуле:


Кх = Ку = Кz =
- Распределить места по сумме очков в рабочей таблице 1 для каждого теста.
Стандартная Т-шкала
- Занести данные тестирования студентов в таблицу 2.
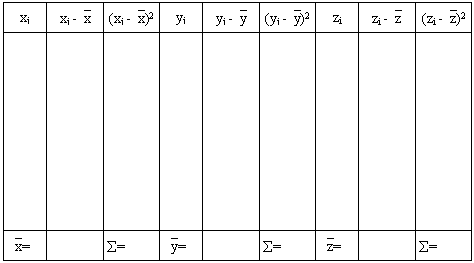

- Рассчитать среднее арифметическое и стандартное отклонение для выборок по формулам:
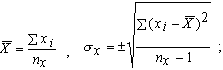
- Рассчитать оценки в каждом тесте по формуле:
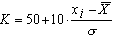
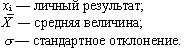
Кх = Ку = Кz =
- Распределить места по сумме очков в рабочей таблице 1 для каждого теста.
Шкала ГЦОЛИФК
- Рассчитать оценки в каждом тесте по формуле:

Кх = Ку = Кz =
- Распределить места по сумме очков в рабочей таблице 1 для каждого теста.
