Методические указания тесты по курсу статистической физики, термодинамики и физики конденсированных сред Ростов-на-Дону

Вид материала

Методические указания

Содержание Тесты по курсу термодинамики, статистической физики и физики конденсированных сред

Подобный материал:

• Рабочая программа Молекулярная физика Специальность 010400 физика, направление 510400-физика, 92.73kb.
• Программа ростов-на-Дону 2007 Конференция осуществляется при финансовой поддержке Российского, 406.02kb.
• Курс лекция по термодинамике и основам статистической физики. Основные положения термодинамики, 21.47kb.
• Методические указания к выполнению контрольных работ Для студентов, 327.25kb.
• Алгоритмы и программы Методические указания для подготовительных курсов Ростов-на-Дону, 1376kb.
• Методические указания для подготовительных курсов Ростов-на-Дону, 445.48kb.
• Академии наук, 6712.96kb.
• Учебно-методический комплекс по дисциплине Линейные и нелинейные уравнения физики (Методы, 325.5kb.
• Программа и планы семинарских занятий по курсу Организация и техника внешнеэкономической, 296.92kb.
• Паспорт специальности 01. 04. 07 – физика конденсированного состояния, 1004.81kb.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»


МЕТОДИЧЕСКИЕ УКАЗАНИЯ


Тесты по курсу статистической физики, термодинамики и физики конденсированных сред


Ростов-на-Дону

2005

Методические указания разработаны кандидатом физико-математических наук, доцентом кафедры теоретической и вычислительной физики В.А.Бейлиным.


Ответственный редактор доктор физ.-мат. наук,

профессор В.П. Саченко


Компьютерный набор и верстка В.А. Бейлина


Печатается в соответствии с решением кафедры теоретической и вычислительной физики физического факультета РГУ, протокол № 2 от 6 сентября 2005 г.


Тесты по курсу термодинамики, статистической физики и физики конденсированных сред


Представленные в настоящем методическом пособии вопросы, относящиеся к различным разделам курса, безусловно, не позволяют изучить весь курс статистической физики, термодинамики и физики конденсированных сред — даже при наличии верных ответов на все вопросы. И дело даже не в том, что данный набор вопросов далеко не исчерпывает всего богатства физического содержания предмета, просто цель представленного пособия иная: дать возможность студентам проверить свои знания не в практическом курсе решения задач, а обдумывая (и находя) ответы на вопросы теоретического содержания. Безусловно, для ответа на некоторые вопросы имеет смысл держать под рукой ручку и бумагу — некоторые догадки полезно проверить, т.е. «поверить алгеброй гармонию», для чего следует провести необходимые выкладки. Зачастую вопросы сформулированы так, что выбор ответа не является очевидным, поэтому поиск верного ответа представляет собой не просто «сканирование» теоретического материала — текста лекций или учебников, но процесс анализа почти каждого из приведенных варианта ответов. Именно это и представляется автору полезным занятием для тех, кто намерен разобраться в способах и методах исследования структуры и эволюции макроскопических систем.

1. Предметом исследования в статистической физике являются:
   

а) взаимодействия частиц (атомов, молекул или их комплексов), из которых состоит любая система;

б) методы квантовомеханического описания свойств систем, состоящих из большого числа частиц;

в) особые закономерности, описывающие свойства и поведение систем с макроскопически большим числом частиц ( 10²⁴).

2. Уравнения Гамильтона классической механики:
   

а) позволяют получить все соотношения статистической физики путем усреднения по всем возможным координатам и импульсам частиц;

б) описывают только поведение отдельных частиц при заданном гамильтониане всей системы;

в) не выводятся, как частный случай, из классического уравнения Лиувилля для функции Н(p,q).

3. Энергия замкнутой макроскопической системы:
   

а) в статистической физике не может рассматриваться как функция только макроскопических параметров P и V;

б) является функцией только температуры;

в) не зависит от микроскопических характеристик — например, импульсов, координат — отдельных частиц системы.

4. В рамках термодинамического метода устанавливаются:
   

а) феноменологические закономерности поведения систем с большим числом частиц;

б) траектории движения отдельных частиц в системе;

в) закономерности эволюции микросостояний системы.

5. В рамках классической гамильтоновой механики точное описание макроскопических систем:
   

а) невозможно, ввиду принципиальной незамкнутости любой макросистемы;

б) невозможно, поскольку практически нереально решить систему уравнений Гамильтона для числа частиц  10²⁴;

в) возможно после задания начальных условий для соответствующей системы уравнений.

6. Начальные условия:
   

а) полностью задают статистические характеристики системы;

б) необходимо задавать при вычислении средних значений динамических функций системы;

в) несущественны при статистическом описании макроскопических систем.

7. Статистическим весом макроскопического состояния называется:
   

а) число частиц, находящихся в данном макросостоянии;

б) число микроскопических состояний, которым соответствует одно наблюдаемое макросостояние;

в) число частиц в макросистеме при фиксированной ее температуре.

8. Основной постулат статистической физики — это:
   

а) утверждение о равенстве вероятностей реализации различных микросостояний, соответствующих данному макросостоянию изолированной системы;

б) утверждение о необходимости усреднения динамических функций для макросистем с использованием статистического распределения;

в) вывод о направлении теплообмена между двумя телами с разной температурой.

9. Термостат — это:
   

а) любая внешняя среда для данной системы;

б) стационарная внешняя среда для квазизамкнутой системы;

в) внешняя среда, находящаяся всегда при той же температуре, что и рассматриваемая система.

10. Время релаксации макроскопической системы:
    

а) не зависит от плотности частиц и от интенсивности взаимодействия между ними;

б) не зависит от длины свободного пробега частиц, но зависит радиуса действия сил между частицами;

в) тем больше, чем меньше плотность и слабее взаимодействие.

11. При переходе системы в равновесное состояние:
    

а) ее конечное состояние существенно зависит от начального состояния;

б) число параметров, описывающих макроскопическую систему, уменьшается;

в) ее состояние однозначно определяется давлением и объемом.

12. Функция статистического распределения подсистемы:
    

а) зависит от начального состояния других подсистем, с которыми данная подсистема взаимодействует;

б) находится в результате решения системы уравнений для фазовых траекторий всех частиц системы с учетом начальных условий;

в) не зависит от начального состояния рассматриваемой подсистемы и других подсистем.

13. Функция статистического распределения подсистемы:
    

а) позволяет определить статистический вес макросостояния;

б) используется для вычисления средних значения всех микроскопических динамических функций f(r,t,p,q)для данной подсистемы;

в) позволяет вычислять механические, но не тепловые макроскопические наблюдаемые для данной подсистемы путем усреднения микроскопических динамических функций.

14. Эргодическая гипотеза:
    

а) предполагает, что классическая фазовая траектория подсистемы проходит через каждую точку ее фазового пространства бесконечное множество раз за время жизни подсистемы;

б) всегда верна для любой известной макроскопической системы;

в) не справедлива, если некоторые степени свободы подсистемы недоступны в определенных условиях или по причинам динамического характера.

15. Взаимодействие между квазизамкнутыми подсистемами:
    

а) настолько мало, что при переходе системы в целом к равновесию им можно пренебречь;

б) не зависит от числа частиц в подсистемах;

в) необходимо учитывать при рассмотрении релаксации системы в целом.

16. С точки зрения статистической физики:
    

а) флуктуации наблюдаемых динамических переменных f(r,t) для подсистемы отсутствуют;

б) флуктуации f(r,t) имеются, они не зависят от числа частиц;

в) относительная флуктуация f(r,t) характеризует время пребывания системы в тех областях ее фазового пространства, где мала величина f и уменьшается с ростом числа частиц.

17. Статистический ансамбль — это:
    

а) набор подсистем, находящихся при одинаковой температуре;

б) совокупность различных подсистем, находящихся в одинаковых и неизменных внешних условиях;

в) большое (в пределе — бесконечное) число макроскопически точных копий данной подсистемы, находящихся в одинаковых и неизменных внешних условиях.

18. Классическая теорема Лиувилля:
    

а) справедлива только для замкнутых систем с небольшим числом частиц;

б) приводит к выводу, что функция статистического распределения зависит только от интегралов движения;

в) функция распределения подсистемы постоянна вдоль ее фазовой траектории в течение произвольного промежутка времени.

19. Статистические свойства изолированной системы в состоянии равновесия полностью определяются:
    

а) давлением и температурой системы;

б) статистическим весом системы в состоянии равновесия;

в) значениями семи аддитивных интегралов движения.

20. Микроканоническое распределение для равновесной подсистемы:
    

а) имеет вид (p, q) = const(E(p,q) – E₀) (P(p.q) – P₀) (M(p,q) – M₀), здесь P, M – давление и масса системы;

б) имеет вид (p, q) = const(E(p,q) – E₀) (P(p,q) – P₀) (M(p,q) – M₀), в котором учитывается основной постулат статистической физики;

в) имеет вид (p, q) = constexp(- E(p,q)/T).

21. Статистический оператор в квантовой статистике:
    

а) позволяет находить для подсистемы средние значения всех динамических функций, включая и температуру;

б) используется для нахождения в подсистеме распределения вероятностей по координатам и импульсам одновременно;

в) коммутирует с гамильтонианом замкнутой системы в стационарном состоянии.

22. Функция (Е):
    

а) определяет вероятность для подсистемы находиться в состоянии с энергией Е;

б) задает число состояний подсистемы с энергиями, меньшими Е;

в) определяет число состояний с энергиями в интервале от Е до Е+dE.

23. Распределение по энергиям для равновесной (квази) замкнутой системы
    

а) экспоненциально спадает с ростом энергии;

б) имеет резкий максимум при значении энергии, равном средней энергии;

в) можно использовать для описания свойств системы только для интервалов времени, меньших ее времени релаксации.

24. Энтропия подсистемы в состоянии термодинамического равновесия:
    

а) аддитивная функция температуры и энергии подсистемы;

б) не зависит от числа частиц в подсистеме и определяет расстояние между соседними уровнями в ее энергетическом спектре;

в) безразмерная аддитивная функция статистического веса.

25. Энтропия:
    

а) характеризует средние свойства макросистемы за интервал времени t, больший времени ее релаксации;

б) замкнутой системы достигает максимума или минимума в состоянии полного равновесия в зависимости от начальных условий;

в) характеризует энергетический спектр системы в данный момент времени.

26. Второе начало термодинамики формулируется как:
    

а) энтропия замкнутой системы возрастает;

б) вероятность самопроизвольного выхода системы из состояния равновесия равна нулю;

в) при переходе замкнутой системы из неравновесного состояния в равновесное наиболее вероятно, что S  0.

27. Инвариантность относительно обращения времени
    

а) для микропроцессов существует и в классической, и в квантовой механике;

б) означает реальную обратимость и для любых макропроцессов;

в) не имеет отношения к движению отдельных частиц, а важна только для описания обратимых макроскопических процессов.

28. Термодинамика:
    

а) позволяет вычислять термодинамические параметры макроскопических систем, опираясь на известные данные экспериментов и микроскопической теории;

б) позволяет проанализировать только получаемые из опыта соотношения между различными тепловыми параметрами системы;

в) устанавливает феноменологические соотношения между различными термодинамическими параметрами макроскопических систем.

29. Для системы, состоящей из двух подсистем, находящихся в термодинамическом равновесии:
    

а) вдоль всей системы постоянна величина dS/dE;

б) статистический вес системы равен сумме статистических весов двух ее подсистем;

в) постоянна температура, которая может быть вычислена путем усреднения тепловой функции по статистическому ансамблю.

30. Для макроскопической равновесной системы как целого
    

а) возможно только вращательное движение с независящей от температуры скоростью;

б) невозможны никакие типы движения;

в) скорость поступательного движения пропорциональна температуре.

31. Адиабатический процесс:
    

а) в системе должен протекать так быстро, чтобы отсутствовал теплообмен системы с термостатом, внешние условия фиксированы;

б) протекает в замкнутой системе квазистатически, при этом энтропия возрастает в соответствии со Вторым началом термодинамики;

в) происходит в теплоизолированной системе так, чтобы система в каждый момент времени находилась в состоянии равновесия, соответствующем медленно меняющимся внешним условиям.

32. Из основного термодинамического тождества следует, что:
    

а) при фиксированной энергии энтропия равновесной системы зависит от объема (при отсутствии внешних полей);

б) энергия системы полностью определяется ее объемом и давлением;

в) энтропия замкнутой системы в равновесии определяется только ее температурой.

33. Энергия тела:
    

а) может меняться только за счет работы, совершаемой самой системой;

б) остается неизменной во всех процессах, происходящих с системой;

в) может меняться за счет работы и/или благодаря теплообмену.

34. Полными дифференциалами являются:
    

а) dR и dQ;

б) dR и dE;

в) dS и dE.

35. Термодинамические потенциалы — это:
    

а) функции состояния системы, достигающие минимума при фиксированных энергии и энтропии;

б) аддитивные функции состояния системы, достигающие экстремума в равновесии при фиксированных внешних параметрах, различных для разных потенциалов;

в) функции E(S,V) , E(P,V), E(P.T).

36. Энтальпия:
    

а) функция энергии, давления и объема;

б) остается постоянной в изобарных процессах, происходящих с теплоизолированной системой;

в) в дифференциальной форме dW = S dT – V dP.

37. Изменение свободной энергии:
    

а) равно работе, совершаемой над системой в обратимом изотермическом процессе;

б) равно количеству тепла, получаемого системой в обратимом процессе;

в) в дифференциальной форме dF = -S dT + V dP.

38. Термодинамический потенциал Гиббса:
    

а) достигает максимума в равновесии при постоянной температуре и давлении системы;

б) в дифференциальной форме d = -S dT + V dP;

в) есть аддитивная функция температуры, давления и объема.

39. Все термодинамические потенциалы:
    

а) не зависят от параметров термостата, в котором находится изучаемая система;

б) достигают минимума при фиксированных значениях давления, объема

и температуры системы;

в) функции термодинамически несопряженных параметров состояния.

40. Малые изменения термодинамических потенциалов:
    

а) равны друг другу при произвольных значениях параметров, от которых зависят потенциалы;

б) равны друг другу и обусловлены неконтролируемыми флуктуациями параметров системы в равновесии;

в) обусловлены изменениями внешних параметров и равны при фиксированных значениях термодинамических параметров, разных для различных потенциалов.

41. Уравнение состояния макроскопической системы:
    

а) связывает между собой термодинамически сопряженные параметры;

б) позволяет выразить температуру, давление и объем в одном состоянии через эти же параметры в другом состоянии;

в) связывает между собой температуру, давление и объем в одном и том же состоянии системы.

42. Производная теплоемкости C_V по объему при фиксированной температуре равна:
    

а) T(²P/T²)_V;

б) T(²P/V²)_T;

в) -T(²V/P²)_T.

43. Какое из нижеследующих соотношений Максвелла верно:
    

а) (S/P)_V = - (V/T)_S;

б) (S/P)_V = - (T/V)_P;

в) (S/T)_V = (P/V)_T.

44. Дать определение якобиана перехода в случае функции двух переменных и выписать основные свойства якобианов.
    

45. Какое из тождеств верно:
    

а) (T,S)/(P,V) = -1;

б) (T,S)/(P,V) = 0;

в) (T,S)/(P,V) = 1.

46. Проверить с использованием метода якобианов, что при адиабатическом расширении при условии (V)/(T)_P < 0:
    

а) температура системы падает;

б) температура системы растет;

в) температура системы остается неизменной.

47. Проверить с использованием метода якобианов, что адиабатическая сжимаемость:
    

а) равна изотермической сжимаемости при условии C_P > C_V;

б) меньше изотермической сжимаемости при условии C_P < C_V;

в) меньше изотермической сжимаемости при условии C_P > C_V.

48. По данным эксперимента можно установить (с точностью до констант) значения всех термодинамических потенциалов:
    

а) измеряя ход температурной зависимости C_V= C_V(T) в интервале температур [T₀, T] и значение энтропии при абсолютном нуле;

б) измеряя ход температурной зависимости C_P = C_P(T) в некотором интервале температур [T₀, T] и значение энтальпии при температуре T₀;

в) измеряя в некотором интервале [T₀, T] зависимость коэффициента теплового расширения от температуры.

49. В процессе Джоуля – Томсона:
    

а) давления по обе стороны пористой перегородки поддерживаются постоянными и равными, процесс необратим;

б) свободная энергия газа в необратимом процессе стационарного перехода из объема V₁ в объем V₂ остается неизменной;

в) возрастает энтропия, а энтальпия не меняется.

50. При расширении газа в пустоту:
    

а) сохраняется свободная энергия газа, так как его температура остается постоянной;

б) сохраняется энергия в нестационарном процессе расширения;

в) энтропия газа остается постоянной при уменьшении давления газа.

51. Тепловые машины:
    

а) выполняют полезную работу только при наличии не менее трех тел с различными температурами;

б) позволяют получить максимальную работу в квазистатическом (обратимом) процессе;

в) совершают работу только при переходе из неравновесного в равновесное состояние, сопровождаемом ростом энтропии.

52. Цикл С.Карно;
    

а) представляет собой обратимую последовательность изотермического, адиабатического, изобарного и изохорного процессов при участии рабочего тела;

б) не может быть практически реализован, поскольку представляет собой идеальный цикл с К.П.Д., равным 1;

в) может быть изображен в виде прямоугольника в осях «Температура – Энтропия».

53. В произвольном обратимом цикле:
    

а) ;

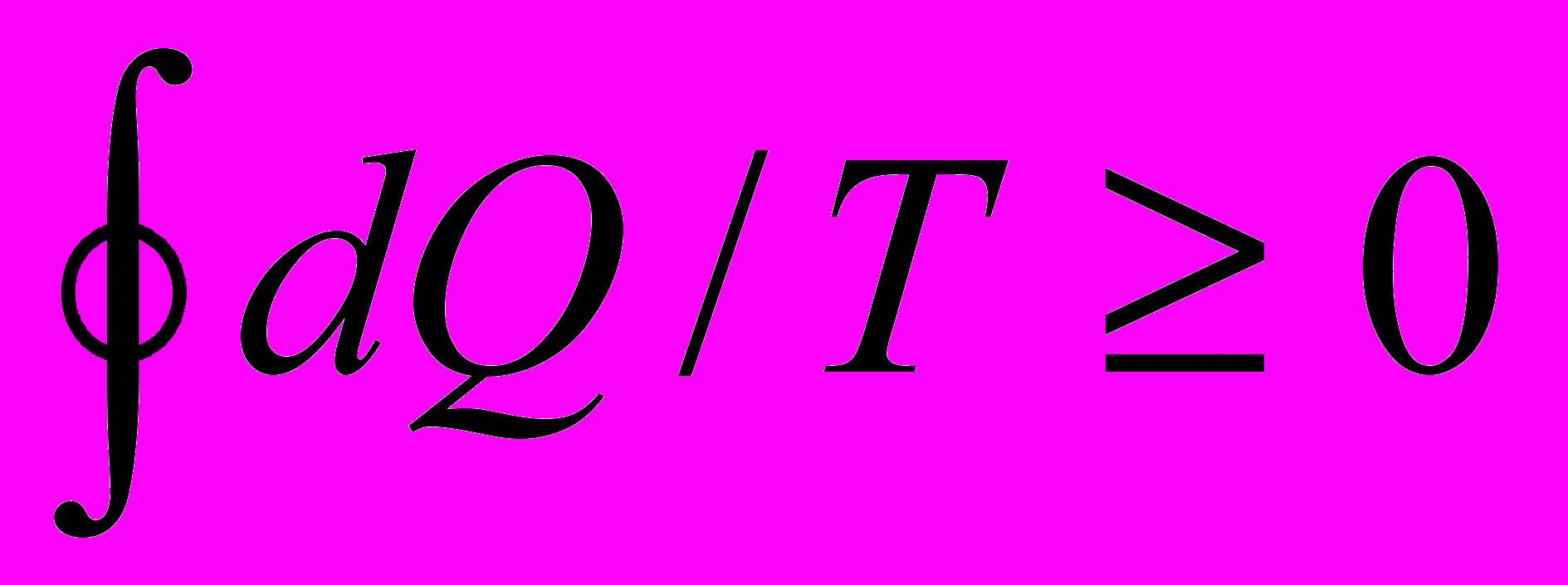б) ;

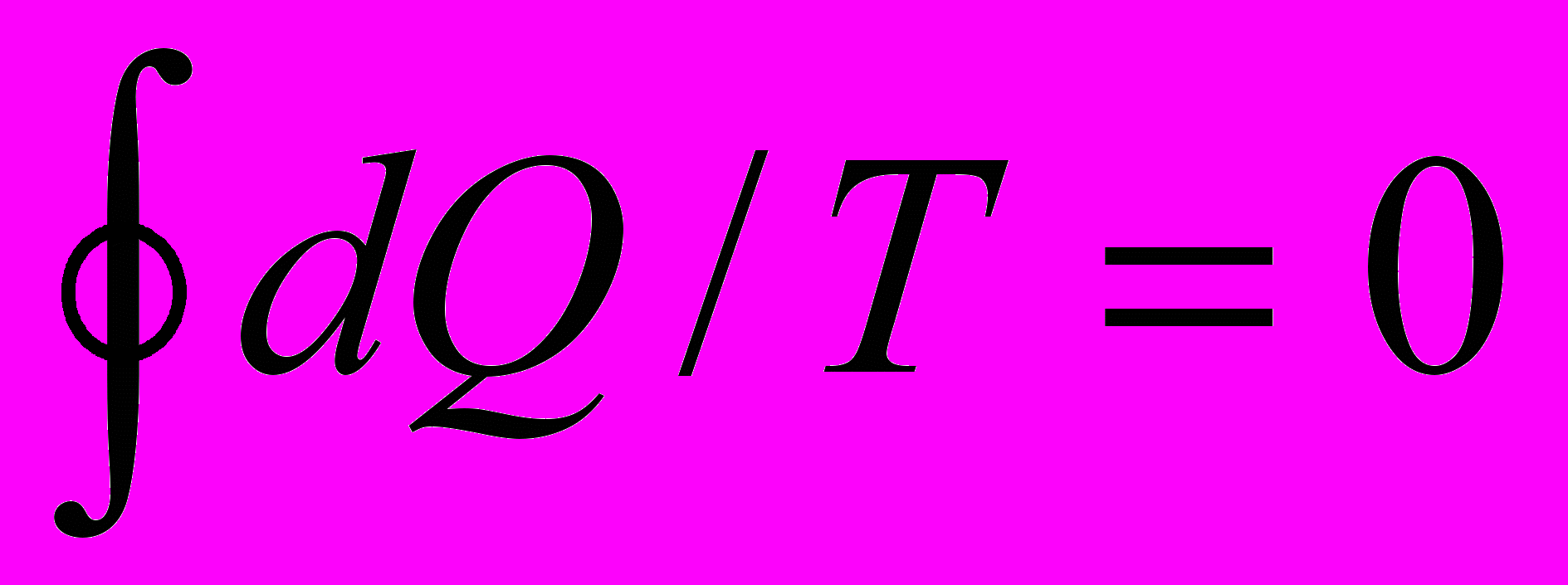в) энтропия остается постоянной в любой момент времени.

54. Тело, находящееся в термостате
    

а) может совершить работу над некоторой теплоизолированной подсистемой в обратимом круговом процессе;

б) совершает максимальную работу в некруговом процессе, при неизменных объеме и температуре тела эта работа равна изменению свободной энергии тела;

в) совершает максимальную работу над подсистемой адиабатически, работа равна изменению внутренней энергии системы.

55. Однородное тело в равновесии
    

а) устойчиво, если C_P > C_V > 0 и T/S < 0;

б) устойчиво, если C_P > C_V > 0 и P/S < 0;

в) устойчиво, если (W/T)_P > (E/T)_V > 0

и P/V < 0.

56. Условие C_V > 0 означает, что:
    

а) с ростом температуры энтальпия системы растет;

б) с уменьшением объема возрастает энтропия;

в) уменьшение энергии системы при падении температуры.

57. Третье начало термодинамики:
    

а) указывает на стремление к нулю энтальпии системы при уменьшении температуры до 0⁰С;

б) содержит и утверждение о стремлении к нулю теплоемкостей при уменьшении температуры до 0 К;

в) говорит о равенстве нулю энтропии любого тела при температуре, равной 0 К.

58. Аддитивные характеристики системы —
    

а) могут зависеть только от аддитивных же параметров, т.е. не зависят от температуры системы;

б) это ее энергия, энтальпия и энтропия;

в) прямо пропорциональны числу частиц в системе.

59. Химический потенциал системы
    

а) это свободная энергия системы, приходящаяся на одну частицу;

б)  = (W/N)_S,P;

в) зависит от температуры и объема системы.

60.  - потенциал системы
    

а) зависит от энтропии и числа частиц в системе;

б) зависит от давления и объема системы;

в) достигает экстремума в состоянии равновесия при фиксированных температуре, химическом потенциале и объеме.

61. Если две подсистемы могут в равновесии обмениваться частицами, находясь во внешнем стационарном поле, то
    

а) равны температуры и давления подсистем, но различны производные (S/N)_E,T;

б) равны температуры, давления и значения производных (S/N)_E,T;

в) равны температуры и химические потенциалы систем.

62. Принцип Ле-Шателье
    

а) описывает только реакцию системы на изменение ее температуры или давления;

б) описывает тип перехода системы из неравновесного в равновесное состояние;

в) указывает характер реакции системы на внешнее воздействие, выводящее систему из состояния равновесия.

63. Каноническое распределение:
    

а) устанавливает вероятность обнаружения замкнутой микроскопической системы в состоянии с энергией Е = Е_n;

б) указывает вероятность обнаружения в состоянии с энергией Е_n сравнительно малой и квазизамкнутой подсистемы в термостате;

в) задает распределение вероятностей по энергии для любой макроскопической подсистемы большого термостата.

64. Распределение Гиббса по энергии:
    

а) при большом числе частиц в подсистеме ведет себя практически как микроканоническое;

б) представляет собой гладкую монотонно убывающую функцию энергии;

в) имеет резкий максимум вблизи среднего значения энергии подсистемы, точно так же, как и распределение Гиббса по квантовым состояниям.

65. Свободная энергия системы F:
    

а) может быть вычислена, если известен спектр энергетических состояний подсистемы;

б) в классическом случае для любой системы определяется энергетическим спектром одной частицы;

в) одна и та же для различных систем при одной и той же температуре.

66. Классическое распределение Максвелла:
    

а) не зависит от координат частиц в любой системе;

б) позволяет находить распределения по импульсам и координатам независимо друг от друга;

в) выводится без использования распределения Гиббса и только при отсутствии внешнего силового поля.

67. Для макроскопической системы квантовых осцилляторов:
    

а) распределение по координатам не сводится к классическому распределению при любой температуре;

б) распределение по импульсам отличается от распределения Максвелла по импульсам классических частиц;

в) распределения по координатам и импульсам сводятся к классическим распределениям при T>>hw/2.

68. Если в состоянии термодинамического равновесия между подсистемами в термостате может происходить обмен одинаковыми частицами, то:
    

а) энергия n-го квантового состояния подсистемы и ее энтропия не зависят от числа частиц N в подсистеме;

б) химический потенциал термостата равен химическому потенциалу подсистемы;

в) энергия рассматриваемой подсистемы не должна слишком отличаться от энергии термостата.

69.  - потенциал:
    

а) является функцией температуры и давления системы;

б) не зависит от объема и температуры системы;

в) определяет нормировочный коэффициент для большого канонического распределения.

70. Сравнение различных распределений, применяемых в статистической физике, показывает, что:
    

а) проще всего применять для расчетов средних значений различных динамических функций микроканоническое распределение;

б) большое распределение Гиббса, в отличие от микроканонического и канонического распределений, учитывает помимо флуктуаций энергии также и флуктуации числа частиц в подсистеме;

в) каноническое распределение так же, как и микроканоническое, опирается на гипотезу о равнораспределении (постулат об априорных вероятностях).

71. Для открытой подсистемы:
    

а) можно вычислить лишь среднее число частиц в ней, зная свободную энергию подсистемы;

б) можно вычислить среднее число частиц и среднеквадратичное отклонение от него, зная  - потенциал подсистемы;

в) число частиц в подсистеме, находящейся в состоянии термодинамического равновесия со средой, является постоянной величиной.

72. Идеальный газ — это:
    

а) статистическая система, энергетический спектр которой полностью определяется энергетическим спектром одной частицы;

б) макроскопическая система частиц, невзаимодействующих между собой силовым образом и соударяющихся только со стенками сосуда;

в) макроскопическая система частиц, энергия взаимодействия между которыми пренебрежимо мала по сравнению с полной энергией системы, а радиус действия сил между частицами  ( — длина свободного пробега частиц).

73. В идеальном газе:
    

а) каждую отдельную частицу можно считать квазизамкнутой подсистемой, которая подчиняется распределению Гиббса;

б) нельзя применять распределение Гиббса к подсистеме частиц, находящихся в одном и том же квантовом состоянии;

в) нужно использовать распределение Больцмана, а не распределение Гиббса.

74. Классическое распределение Больцмана:
    

а) может быть применено ко всем степеням свободы частицы, включая и ее внутренние степени свободы;

б) при отсутствии внешнего поля совпадает с максвелловским распределением по импульсам (или скоростям) частиц;

в) имеет вид

dN = ,

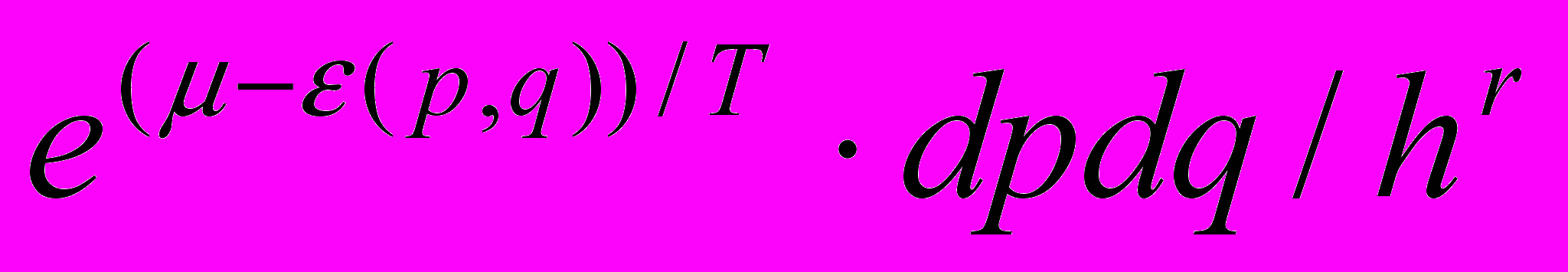где r – число степеней свободы системы.

75. Среднее число соударений молекул:
    

а) со стенками сосуда не зависит от температуры газа в состоянии термодинамического равновесия;

б) между собой не зависит от характеристик процесса рассеяния (сечения рассеяния, например) частиц друг на друге;

в) друг с другом может быть вычислено с использованием распределения Максвелла по скоростям (относительным) частиц.

76. Свободная энергия больцмановского идеального газа:
    

а) в классическом случае пропорциональна 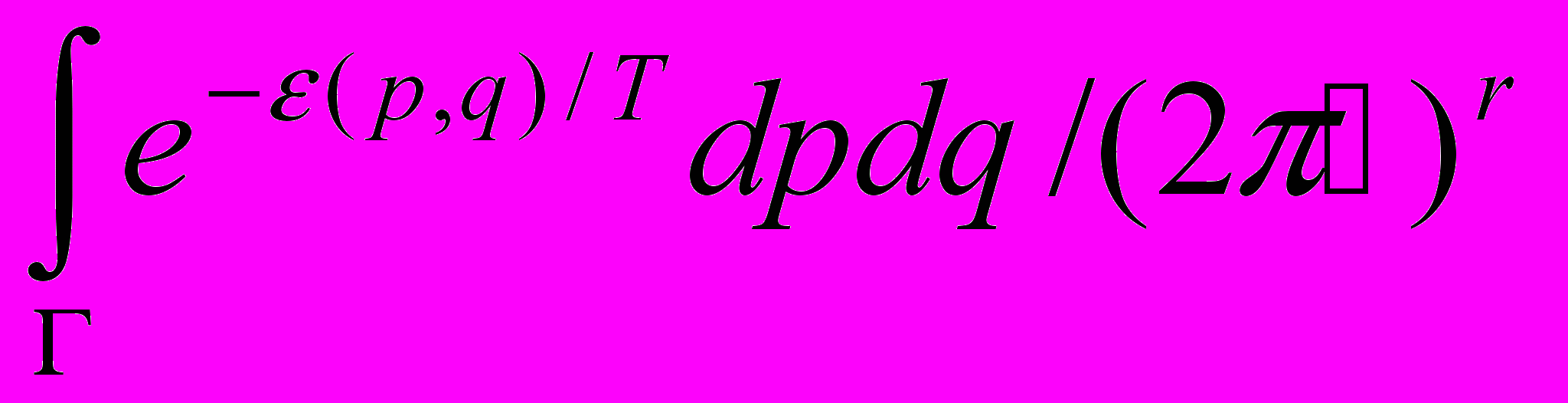, где интегрирование идет по фазовому объему одной частицы;

б) не зависит от полного числа частиц в системе;

в) определяется статистической суммой по квантовым состояниям всего газа, причем указанная статсумма не выражается через статистическую сумму по состояниям одной частицы.


77. Уравнение состояния идеального газа:

а) определяет внутреннюю энергию идеального газа, как функцию его давления и энтропии;

б) задает зависимость давления газа от его объема и энергии;

в) позволяет вычислить температуру газа при заданных числе частиц, давлении и объеме газа.


78. Теплоемкость идеального газа:

а) зависит только от его температуры;

б) только в процессах, происходящих при постоянном объеме, зависит от температуры газа и числа частиц;

в) не зависит от температуры в любом процессе.

79. Для газа с постоянной теплоемкостью:
    

а) внутренняя энергия зависит от температуры и энтропии;

б) энтропия S = N(– lnP+c_PlnT +c_P);

в) энтальпия W = Nc_VlnT + N₀.

79. Уравнение адиабаты:
    

а) для любого идеального газа имеет вид PV^ = const;

б) вида T^ P^1- = const имеет место только при постоянном числе частиц N;

в) описывает процесс, происходящий с теплоизолированным идеальным газом при постоянной энтальпии.

79. Число колебательных степеней свободы L:
    

а) не зависит от числа атомов в молекуле и равно 3 для линейных молекул;

б) равно L = 6n – 6 для любого типа молекул, n – число атомов в молекуле;

в) для n- атомной нелинейной молекулы L  L_вр, L_вр – число вращательных степеней свободы.

79. Закон равнораспределения для классического идеального газа:
    

а) означает, что все степени свободы частиц, из которых состоит газ, вносят в энергию вклад, равный Т/2;

б) утверждает, что вращательные и колебательные степени свободы частиц вносят в теплоемкость газа равные вклады, по ½;

в) каждая переменная в одночастичной энергии, как функции координат и импульсов, вносит равный вклад, по ½, в теплоемкость газа.

79. Вычисление свободной энергии для одноатомного идеального газа:
    

а) имеет смысл проводить при температурах Т<< E_{ионизации}, чтобы считать атомы находящимися на низшем энергетическом уровне;

б) можно проводить при любой температуре газа;

в) не требует нахождения статистической суммы по вращательным и электронным квантовым состояниям.

79. Статистика Больцмана для описания газа:
    

а) применима, если при фиксированной плотности газа его температура не слишком мала;

б) может быть использована только при Т<< E_{ионизации}, независимо от плотности газа;

в) неприменима, если газ состоит из тяжелых многоатомных молекул.

79. Энтропия одноатомного идеального газа:
    

а) не стремится к нулю при Т 0, так что теорема Нернста нарушается;

б) стремится к нулю в соответствии с теоремой Нернста;

в) остается постоянной при Т 0, поскольку зависит только от плотности газа.

79. Тонкая структура уровней для одноатомного газа:
    

а) возникает, в частности, когда вырождение энергетических уровней с фиксированными значениями L и S снимается малым (по сравнению с электростатическим) релятивистским взаимодействием;

б) означает возникновение 2L + 1 компонент тонкой структуры уровня;

в) не влияет на значение статистической суммы для газа при любых температурах.

79. Для двухатомных газов с гетерогенными молекулами:
    

а) энергия молекулы не зависит от энергии кулоновского взаимодействия электронов с ядрами и между собой;

б) полная статистическая сумма имеет вид Z =Z_вращ. Z_{колебат.};

в) колебательная часть свободной энергии при высоких температурах (причем Т<диссоциации) пренебрежимо мала по сравнению с F_вращ.

79. Для двухатомного газа с гетерогенными молекулами:
    

а) при низких температурах (Т<<²/2 I) энергия, связанная с вращением молекулы, экспоненциально мала;

б) не существует никакого интервала температур, когда двухатомный газ ведет себя, как одноатомный;

в) вклад колебательных степеней свободы в теплоемкость равен единице.

79. Парадокс Гиббса для смеси двух идеальных газов состоит в том, что:
    

а) изменение энтропии газов после их смешения зависит от того, одинаков ли тип молекул смешиваемых газов;

б) давление в смеси газов не равно сумме их парциальных давлений;

в) энтропия смеси газов оказывается независящей от числа частиц в смешиваемых газах.

79. При понижении температуры Т до нуля:
    

а) необходимо учитывать относительно небольшие поправки к уравнению состояния идеального газа, однако статистика Больцмана остается справедливой;

б) нужно вводить поправки к распределению Больцмана, обусловленные спином частиц;

в) для систем из частиц с полуцелым спином следует учитывать антисимметричность волновых функций.

79. Появление конденсата в системах частиц с целым спином:
    

а) означает возникновение в них при понижении температуры подсистем частиц с нулевым импульсом;

б) происходит только при температуре Т = 0;

в) происходит точно так же, как в системах фермионов при температуре, меньшей энергии Ферми.

79. Химический потенциал электронного газа:
    

а) при Т = 0 равен максимально возможной энергии электронов в этой системе, т.е. энергии уровня Ферми;

б) при температуре, близкой к нулю, становится отрицательным;

в) при низких температурах не зависит от плотности системы, а при Т = 0 обращается в ноль.

79. Для ультрарелятивистской системы:
    

а) уравнение состояния имеет вид Р = /3 независимо от спина частиц;

б) уравнение состояния совпадает с уравнением состояния идеального газа;

в) давление вообще не зависит от плотности частиц, если это система фермионов.

79. Равновесное тепловое излучение:
    

а) можно рассматривать как идеальный газ, поскольку рассеяние фотонов на фотонах крайне мало, и поэтому оно описывается уравнением состояния идеального газа;

б) представляет собой систему бозе-частиц, для которой химический потенциал отрицателен;

в) при низких температурах удовлетворяет закону Релея – Джинса, как частному случаю формулы Планка.

79. Учет неидеальности газа:
    

а) в первом приближении означает учет парных соударений частиц между собой;

б) можно произвести, вводя ненулевые размеры частиц газа и эффективную энергию отталкивания частиц при их сближении до некоторого характерного расстояния;

в) можно всегда произвести, приближенно вычисляя 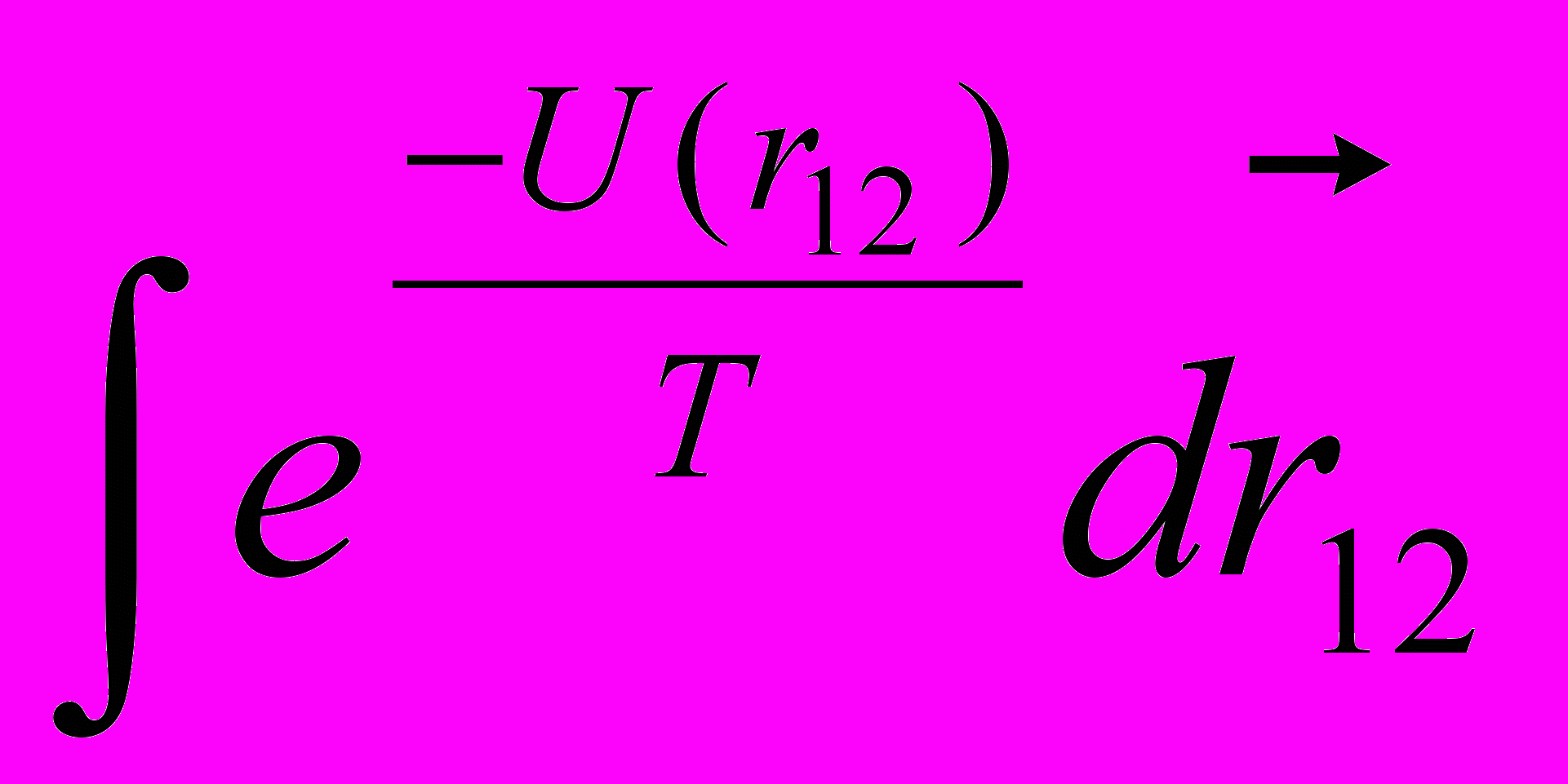при любой зависимости .

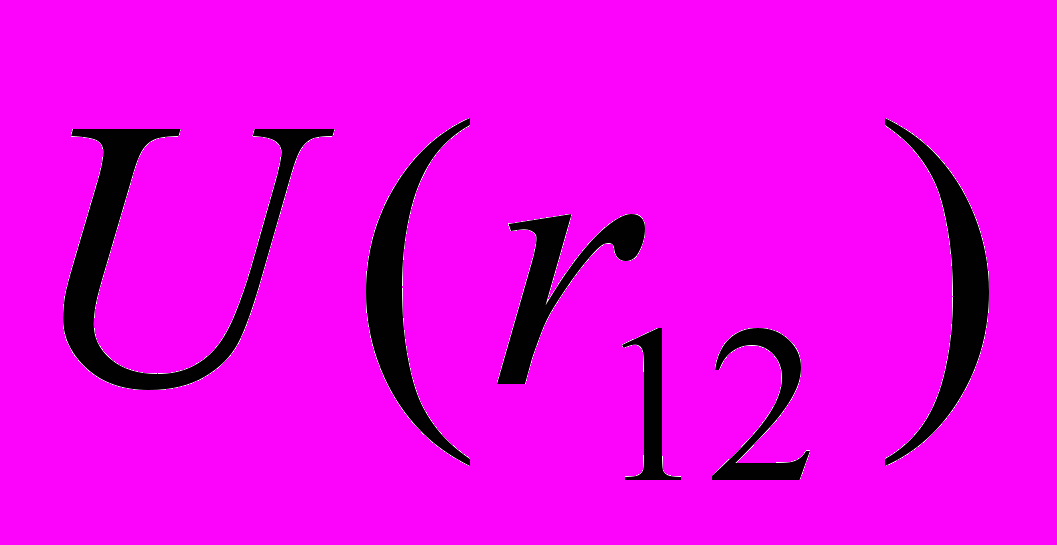79. Интерполяционная формула (уравнение состояния неидеального газа) Ван-дер-Ваальса:
    

а) содержит подгоночные параметры a и b, которые не имеют реального физического смысла и вводятся лишь для того, чтобы этим уравнением состояния можно было описывать реальные системы;

б) графически в осях P – V представлена изотермой, которая одновременно является и изобарой, описывающей фазовый переход I рода между жидкостью и газом;

в) в осях T – V, как и в осях P – V, также изображается одной кривой равновесия фаз.

79. Равновесный переход из одной фазы в другую при фазовом переходе I рода:
    

а) сопровождается выделением или поглощением некоторого количества тепла в соответствии с принципом Ле-Шателье;

б) происходит необратимым образом с выделением количества теплоты q = T(s₂ – s₁),

в) происходит с изменением температуры системы, одновременно радикально меняется симметрия системы.

79. При анализе колебательной статистической суммы твердого тела, как макроскопической системы:
    

а) невозможно ни в каком приближении использовать классическую статистику;

б) при не слишком малых температурах можно трактовать колебательные моды кристалла как звуковые волны;

в) спектр осцилляторов в твердом теле никак не зависит от плотности.

79. Теплоемкость твердого тела:
    

а) при низких температурах не зависит от температуры;

б) при низкой температуре пропорциональна T³;

в) пропорциональна T³ при высоких температурах, когда применима классическая статистика.

79. Интерполяционные формулы в модели Дебая:
    

а) позволяют приближенно вычислить термодинамические функции твердого тела при любой температуре;

б) хорошо воспроизводят поведение теплоемкости твердого тела только при высокой температуре;

в) не содержат зависимости от плотности кристалла.