С. Хабаров "Экспертные системы" (конспект лекций)

Вид материала

Содержание

9.2.Основы теории Демстера–Шеффера
9.3.Меры доверия и правдоподобия в ТДШ
9.4.Отличие ТДШ от теории вероятностей
9.5.Связь между ТДШ и классической теорией вероятностей
9.6.Комбинация функций доверия

Подобный материал:

9.ЭКСПЕРТНЫЕ СИСТЕМЫ НА ОСНОВЕ ТЕОРИИ ДЕМСТЕРА–ШЕФФЕРА

9.1.Предпосылки возникновения новой теории.

При использовании теории вероятностей для представления неопределенных знаний исследователи столкнулись с рядом трудностей. Это стимулировало возникновение новой теории, которая была разработана в 1960 г Демстером и в дальнейшем развита Шеффером (1970 год). Она получила название "теории Демстера-Шеффера" (ТДШ).

Основными предпосылками ее возникновения явилось преодоление ряда ограничений, накладываемых классической теорией вероятностей на предоставление неопределенных знаний. К разряду таких ограничений обычно относят следующие:

представление полного незнания, когда мы ничего не знаем об объекте;
жесткие условия , что требует знания или определения вероятностей всех возможных исходов (гипотез);
фиксирования вероятности отрицательной гипотезы вероятностью прямой гипотезы, т.к.  1.

Первое ограничение связано с тем, что традиционный байесовский подход представляет незнание (неосведомленность) равномерными вероятностями. Некоторый недостаток этого подхода заключается в том, что равномерное распределение вероятности, оказывается, представляет большую информацию, чем дано.

Так, например, если эксперт утверждает, что из всех возможных видов транспортировки груза, мы должны воспользоваться речным транспортом ("РТ"), либо железнодорожным ("ЖД"), то это говорит о степени незнания эксперта и совсем не означает, что вероятности возможной транспортировки будут Р("РТ")=0,5 и Р("ЖД")=0,5.

Второе ограничение определяется тем, что психологически во многих ситуациях эксперту сложно оставаться в рамках строгого математического аппарата теории вероятностей, которая по своей природе носит объективный характер. Необходимо нарушить жесткие условия равенства единице сумм вероятностей всех исходов, особенно при большом их количестве.

В большинстве случаев реально наблюдаемые свидетельства подтверждают не какой-либо конкретный исход (или гипотезу) а сразу же некоторое множество, что не позволяет определить вероятность каждого из них. Так, если мы на 90% уверены в том, что промчавшийся мимо нас автомобиль - это "Жигули", то эта масса уверенности (m₁=0.9) относится ко всем моделям "Жигулей", а масса уверенности m₂=0.1 – ко всем прочим маркам легковых автомобилей, причем более детальное её распределение нам неизвестно.

Что касается третьего ограничения, то, как следует из множества реальных ситуаций, свидетельства, которые только частично поддерживают гипотезу не следует рассматривать как свидельство также поддерживающее отрицание гипотезы.

9.2.Основы теории Демстера–Шеффера

Прежде всего, остановимся на основных понятиях и определениях ТДШ. Возможно, наиболее основным понятием этой теории является фрейм различения , определяемый как полное множество взаимоисключающих событий. Роль фрейма различения  в ТДШ такая же, как роль выборочного пространства  в теории вероятностей. Однако отличие заключается в том, что если в теории вероятностей число возможных гипотез равно

, то в ТДШ число возможных гипотез равно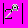

и представляет собой все возможные подмножества .

Пример 1. Пусть полное множество взаимоисключаемых событий связанных с перевозкой груза включает в себя 4 события, определяющие перевозки железнодорожным (ЖД), автомобильным (Авто), морским (МТ) и авиационным (Авиа) транспортом. В этом случае фрейм различения , как и выборочное пространство , имеют по 4 элемента. Но если в теории вероятностей число возможных гипотез равно 4: Н₁={Авто}; H₂={МТ}; H₃={ЖД}; H₄={Авиа}, то в ТДШ число возможных гипотез будет 2⁴= 16:

	События
i	ЖД	Авто	МТ	Авиа	A_i (гипотезы)
0	0	0	0	0	{}
1	0	0	0	1	{Авиа}
2	0	0	1	0	{МТ}
3	0	0	1	1	{МТ, Авиа}
4	0	1	1	0	{Авто}
-	-	-	-	-	-
7	0	1	1	1	{Авто, МТ, Авиа}
-	-	-	-	-	-
15	1	1	1	1	{ЖД, Авто, МТ, Авто}

ТДШ несколько по-иному трактует не только понятие гипотезы, но и её отрицание в теории Демстера - Шеффера:

гипотеза А означает "А и только А"

в то время как

А означает "что угодно, но не А".

То есть ТДШ рассматривает наблюдение свидетельств против гипотезы как свидетельства поддержки отрицания гипотезы.

Пример 2. Если мы воспользуемся определениями гипотез из примера 1, то свидетельства, нарушающие гипотезу А={Авто} (т.е. автомобильный и только автомобильный транспорт) эквивалентно свидетельству, поддерживающему гипотезу А={МТ, ЖД, Авиа} (т.е. что угодно, но не автомобильный транспорт)

Рассмотрим еще одно фундаментальное понятие ТДШ, а именно понятие базовой вероятности. Пусть А - некоторое подмножество . Основная мера вероятности, обозначаемая m(A), - это базовая вероятность, приписываемая множеству А. Величина m(A) может рассматриваться как порция (или доля) от общего доверия, назначаемая точно А. Во многих аспектах это число может рассматриваться подобно обычной вероятности.

Функции р(А) и m(A) в первую очередь отличаются тем, что в теории вероятностей А должно быть отдельным элементом, в то время как в ТДШ А может содержать несколько элементов, т.е. являться множеством. Базовые вероятности должны удовлетворять двум основным свойствам:

1) базовая вероятность нулевого события равна 0 , т.е. m()=0

2) сумма базовых вероятностей для всех подмножеств фрейма различения  равна 1, т.е.

= 1.

Пример 3. Пусть в результате экспертного оценивания возможности транспортировки грузов 30% экспертов высказывались за использование автотранспорта, 20% - за железнодорожный, 10% - за морской, а 40% - за использование либо автомобильного, либо железнодорожного транспорта (не выделив предпочтение одного из них). Тогда базовые вероятности, назначаемые как порции от общего доверия экспертов к возможным транспортировкам, будут иметь значение:

m({Авто}) =0.3; m({ЖД})=0.2; m({МТ})=0.1

m({Авто, ЖД})=0.4

m(Ai)=0 во всех остальных 12-ти случаях

При этом должно выполняться второе свойство базовых вероятностей, т.е.

= m({Авто}) + m({ЖД}) + m({МТ}) + m({Авто, ЖД}) = 1

Отметим ещё одну особенность ТДШ по сравнению с теорией вероятностей. Так как А может являться не только конкретным элементом, но и множеством, то это позволяет задавать оценки базовых вероятностей для интервалов изменения случайных величин, не зная их законов распределения на этих интервалах.

Так, например, если в рамках теории вероятностей эксперт может предположить, что прибыль фирмы будет 50 тыс. руб. с вероятностью Р(50)=0.5, 60 тыс. руб. с вероятностью Р(60)=0.2 и т.д. для всех вероятных исходов, то в рамках ТДШ эксперт может дать следующие оценки прибыли фирмы: от 50 до 70 тыс. руб. с вероятностью m(50 70)=0.4, от 60 до 80 тыс. руб. с вероятностью m(60  80)=0.3

Другими словами, если для определения вероятности некоторой совокупности событий при использовании теории вероятностей необходимо знать вероятности всех элементарных исходов, то при использовании ТДШ это не обязательно. Однако платой за это является возможность получения только интервальных оценок, к способам, определения которых мы и переходим.

9.3.Меры доверия и правдоподобия в ТДШ

Мера доверия А, обозначаемая Bel(A), измеряет полное число доверий в А. Математически это может быть выражено, как

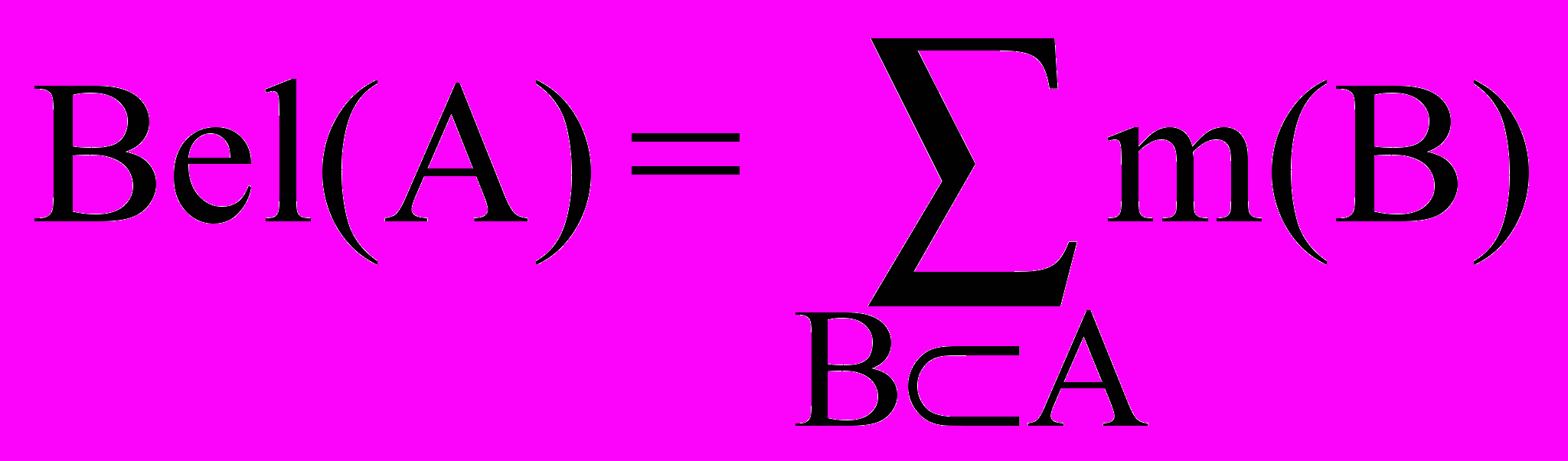
Функция Bel() называется функцией доверия (от англ. believe - доверять), если она удовлетворяет следующим условиям:

1) Доверие к нулевой гипотезе равно 0, т.е. Bel()=0

2) Доверие ко всему фрейму различения равно 1, т.е. Bel ()=1

3) Сумма доверий А и А должна быть  1, т.е. Bel(А) + Bel(А)  1

Таким образом, функция доверия будет равна базовым вероятностям в случае множеств, состоящих из одного элемента (элементарного исхода), и будет больше или равна базовым вероятностям для множеств, содержащих более одного элемента, т.е.

Bel(А) = m(A), если А - множество из одного элемента,

Bel(А) m(A), если А - содержит более одного элемента.

Пример 4. Для случая базовых вероятностей, определенных в примере 3 функции доверия будут иметь вид:

Bel ({Авто}) = m ({Авто}) = 0.3,

но Bel ({Авто, ЖД}) = m ({Авто, ЖД}) + m ({Авто}) + m ({ЖД})  m ({Авто, ЖД}),

т.е. Bel({Авто, ЖД}) = 0.4 + 0.3+0.2 = 0.9 > 0.4

Задав функцию доверия можно определить несколько вспомогательных характеристик. Величина 1 - Bel(А) называется правдоподобием множества

и обозначается Pl (A) (от англ. plausibility - правдоподобие), т.е.

Pl(A) = 1 - Bel( A) = 1 -

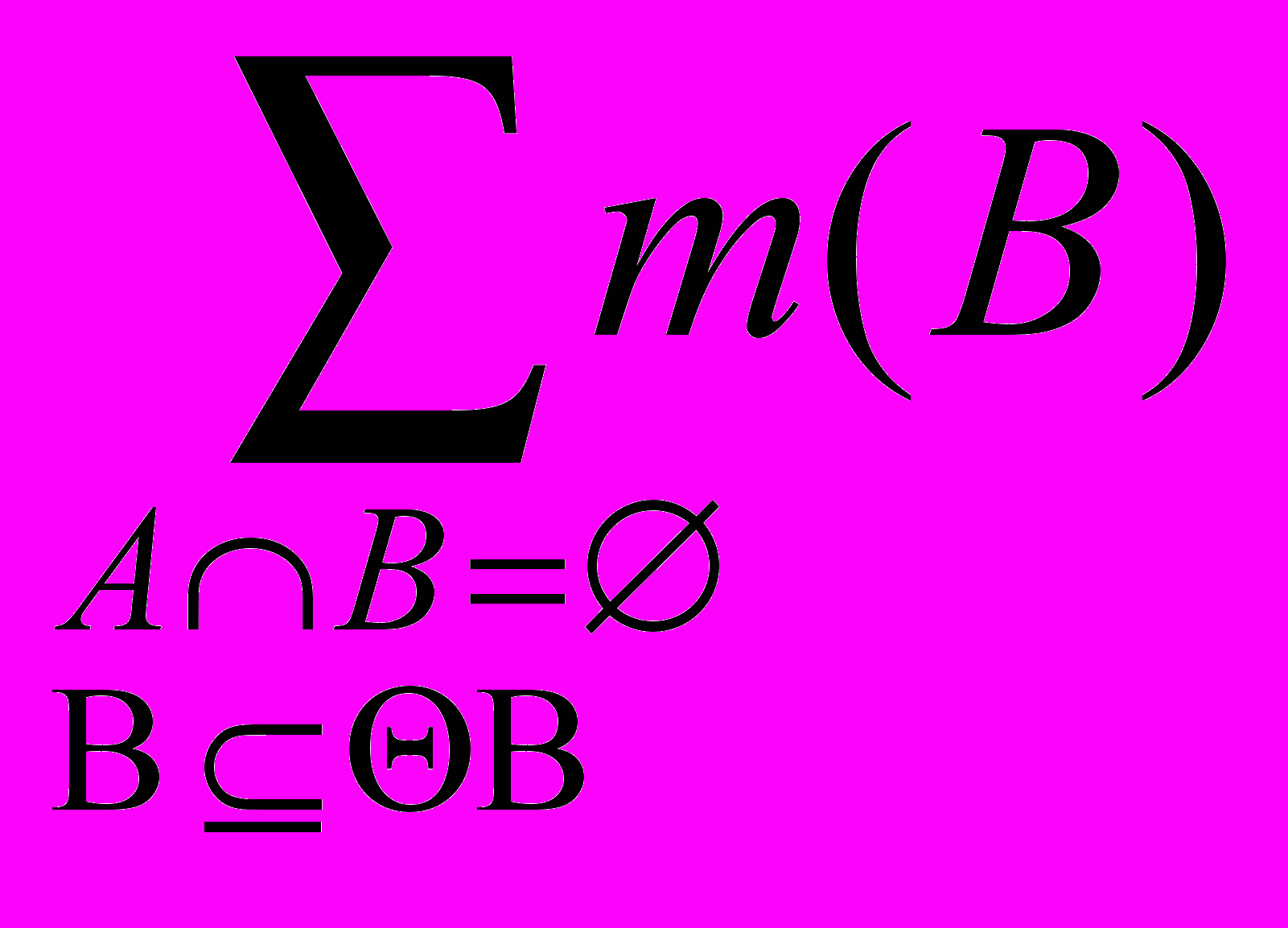
Эта величина определяет максимальное значение степени доверия, которое может быть по возможности назначено А. Функции Bel(A) и Pl(A) можно интерпретировать как нижние и верхние вероятности множеств

в том смысле, что предполагается существование некоторой истинной вероятности Р(А):

Bel(A)  P(A)  Pl(A), для

.

Это следует из того факта, что из свойств функции доверия

Bel(A) + Bel( А)  1,

тогда

Bel(A)  1 - Bel(А)

и

Bel(A)  Pl(A).

Пример 5. На основе предыдущих примеров, функция правдоподобия для А={Авто}   будет иметь вид:

Pl({Авто}) = 1 - Bel({Авто}) = 1 - Bel({ЖД, Авиа, МТ}) =

= 1 - (m({ЖД}) + m({МТ}) = 1 - (0.2 + 0.1) = 0.7

Откуда следует, что некоторая истинная вероятность события, связанного с транспортировкой груза автомобильным транспортом на основе мнений экспертов будет 0.3P({Авто})  0.7

Следует отметить, что в ТДШ рассматриваются не все подмножества фрейма различения, а только те, которые имеют ненулевые базовые вероятности. Каждое из этих подмножеств называется фокальным элементом функции доверия Bel.

Другими словами, если m(A) > 0, то

- фокальный элемент распределенного доверия на множестве . Объединение всех фокальных элементов для функции доверия называется его ядром. Для рассматриваемого нами примера фокальными элементами функции доверия являются

{Авто}, {ЖД}, {МТ}, {Авто, ЖД},

а их объединение образует ядро функции доверия

{Авто, ЖД, МТ} = {Авто}  {ЖД}  {МТ}  {Авто, ЖД}.

9.4.Отличие ТДШ от теории вероятностей

В теории вероятностей, равномерное априорное распределение описывает полное незнание. Однако это не делает различие между полным незнанием и знанием, что случайная величина или событие равномерно распределено.

С другой стороны ТДШ выражает незнания явно. Например, если А и В – только гипотезы, то в теории вероятностей незнание об А и В выражается, как Р(А)=Р(В) = ¹/₂. В ТДШ, m({A}) = m({В}) = ¹/₂ показывает, что доверия к А и В одинаковы, но нет незнания.

Функция доверия, в этом случае, называется байесовской функцией доверия. То есть, если все фокальные элементы – отдельные элементы (элементарные события), то не существует незнания относительно их возникновения. Если некоторый фокальный элемент содержит более чем один элемент, то существует некоторое незнание.

В теории вероятностей, вероятность отрицания гипотезы фиксируется, если известна вероятность А, т.к. A  A =  и p(A) + p(A) = 1. Аналогичный результат в ТДШ дает Bel(A) + Bel(A)  1.

Однако использование ТДШ ведет к комбинаторному взрыву, т.к. пространство гипотез существенно увеличивается. Чтобы заполнить это пространство, эксперт должен определить все доверия на всех подмножествах пространства возможных гипотез перед тем, как создавать ЭС.

Конечно, эксперт должен определить базовые вероятности только для интересующих его подмножеств, т.к. все остальные подмножества будут иметь нулевые базовые вероятности. В то же время, пока нет эффективной процедуры логического вывода. Это приводит к тому, что в настоящее время не так много систем строится на использовании ТДШ.

9.5.Связь между ТДШ и классической теорией вероятностей

Одной из главных особенностей ТДШ является то, что меры доверия и правдоподобия являются частным случаем интервальных вероятностей, то есть мера доверия – нижняя вероятность, а мера правдоподобия – верхняя вероятность, определённая на вложенных интервалах. Это открывает путь как для построения функции распределения доверий, так и её интерпретации.

Рассмотрим простейший пример, иллюстрирующий связь ТДШ с теорией вероятностей. Пусть оценивается возможность инвестирования финансовых средств либо в производство, либо в ценные бумаги. Для оценки состояния и принятия решения была привлечена группа экспертов, которая разделилась во мнениях и дала следующие оценки:

половина экспертов высказались за инвестирование средств в производство;
вторая половина, не отдав предпочтения какому-либо конкретному виду инвестирования, высказались за то, что возможны вложения, как в производство, так и в ценные бумаги.

Как в условиях заключений этих двух групп экспертов найти вероятность P₁ по вложению инвестиций в производство и вероятность P₂ об инвестициях в ценные бумаги.

Обозначим p(A₁) и p(A₂) доли экспертов, давших первую и вторую оценки. В рассматриваемом примере это будет p(A₁) = 0,5 и p(A₂) = 0,5. Пусть p(B_jA_i) – условная вероятность того, что на j–й вариант инвестирования указывает i–я группа экспертов (j=1,2 и i=1,2). Тогда, следуя классической теории вероятностей и используя формулу полной вероятности, можно записать:

P₁ = P(A₁)  P(B₁A₁) + P(A₂)  P(B₁A₂)

P₂ = P(A₁)  P(B₂A₁) + P(A₂)  P(B₂A₂)

Но если первая группа экспертов чётко определилась с выбором в пользу первого варианта, то есть

P(B₁A₁) = 1 и P(B₂A₁) = 0,

то этого мы не можем сказать о второй группе экспертов. Использование классической теории вероятностей и байесовского подхода к приятию решению приводит к тому, что если у нас нет сведений о распределении вероятности событий (в нашем примере вероятности выбора вариантов инвестирования второй группой экспертов), то принимается, что это распределения равномерное, то есть

P(B₁A₂) = P(B₂A₂) = 0.5

Однако это предположение может быть ошибочным и, принимая его, мы заведомо вносим ошибку или погрешность, нигде не учитываемую при вычислении P₁ и P₂, значения которых в этом случае будут

P₁= 0.5  1 + 0.5  0.5 = 0.75

P₂= 0.5  0 + 0.5  0.5 = 0.25

Можно рассмотреть другой способ расчёта P₁ и P₂. Возьмём крайние случаи, когда условные вероятности выбора варианта инвестирования второй группой экспертов берут:

	P(B₁A₂)	P(B₂A₂)
случай 1	0	1
случай 2	1	0

Тогда расчёт по формуле полной вероятности для каждого из этих случаев даст

	P₁ = P(B₁)	P₂ = P(B₂)
случай 1	0.51 + 0.50 = 0.5	0.50 + 0.51 = 0.5
случай 2	0.51 + 0.51 = 1	0.50 + 0.50 = 0

Таким образом, получены нижние и верхние вероятности, определяющие границы P₁=[0.5; 1] и P₂=[0; 0.5]. Вероятности P₁ и P₂ , соответствующие всем возможным распределениям условных вероятностей р(B_jA_i), находятся в приведённых границах.

Использование ТДШ для этого же примера позволяет на основе мнений каждой из групп экспертов назначить базовые вероятности m({B₁}) = 0.5 и m({B₁ ,B₁}) = 0.5, на основе которых можно определить функции доверия и правдоподобия для каждого из вариантов инвестирования:

Инвестирование в производство	Инвестирование в ценные бумаги
Bel({B₁}) = m({B₁}) = 0.5 Pl({B₁})=1-Bel({B₁})=1-Bel({B₂})=1	Bel({B₂}) = m({B₂}) = 0 Pl({B₂})=1-Bel({B₂})=1-Bel({B₁})=0.5

Из полученных результатов легко видеть, что функции доверия и правдоподобия есть нижние и верхние вероятности, которые в общем случае могут быть получены на основе методов классической теории вероятностей и полностью с ней согласуются.

Вместе с тем следует отметить, что стремление получить с использованием классической теории вероятностей «точную» оценку вероятности является естественным в инженерной практике, но далеко не всегда оправданным. Такая оценка может только ввести в заблуждение относительно принятия решения, а не указывать на реальное состояние дел.

Если вернуться к рассматриваемому примеру, то можно увидеть, что «точная» оценка может быть далека от истинной. Так «точной» оценкой P₁ вместо 0.75 может быть на самом деле любая точка в интервале [0.5; 1].

На ширину интервала существенное влияние оказывает доля экспертов, в высказываниях которых содержится некоторая степень неопределённости или незнания. Если в рассматриваемом примере ³/₄ экспертов можно отнести к первой группе, а ¹/₄ – ко второй, то «точные» оценки по формуле полной вероятности будут иметь вид:

P₁ = 0.75  1 + 0.25  0.5 = 0.875

P₁ = 0.75  0 + 0.25  0.5 = 0.125,

а их верхние и нижние оценки, полученные как с использованием классической теории вероятностей, так и ТДШ позволяют определить их интервальные значения P₁=[0.75; 1] и P₂ = [0; 0.25].

9.6.Комбинация функций доверия

Если текущие свидетельства ведут к множественным довериям относительно одних и тех же гипотез, то доверия необходимо комбинировать для получения общего доверия к гипотезам. Для рассмотрения доверий, ТДШ обычно комбинирует различные функции доверия, вычисляя их ортогональные суммы по правилу Демстера.

Пусть имеем два свидетельства. Одно из них задаётся множеством, определённых на фрейме различения, базовых вероятностей m₁, то есть

и позволяет определить доверия к тем или иным гипотезам. В общем случае ко всем возможным на  гипотезам. При поступлении нового свидетельства также задаётся множеством базовых вероятностей

,

определяющих новое доверие к гипотезам. Если же мы хотим распространить доверие, то есть учесть в логическом выводе оба поступивших свидетельства

,

то для этого необходимо вычислить ортогональные суммы базовых вероятностей, определённых для каждого из свидетельств, то есть

.

Исходя из правила Демстера, ортогональные суммы определяются следующим выражением:

,

где K– нормировочная постоянная, определяемая следующим образом:

.

Если

, то

. Если

, то ортогональная сумма не существует и базовые вероятности m₁ и m₂ противоречивы.

Значение logK называется весом конфликтности между Bel₁ и Bel₂. Таким образом, если Bel₁ и Bel₂не конфликтны, то K = 1. Если Bel₁ и Bel₂полностью противоречивы, то

. Ортогональные суммы являются коммунитативными и ассоциативными.

Рассмотрим пример. Пусть две функции доверия, соответствующие двум свидетельствам, заданным базовыми вероятностями m₁ и m₂, определённым на одном и том же фрейме различения  имеют вид:

свидетельство 1: {m₁({Авто}) = 0.8; m₁ ({}) = 0.2} Bel₁

свидетельство 2: {m₂({Авто, ЖД}) = 0.2; m₂ ({ЖД}) = 0.5 ; m₂ ({}) = 0.3} Bel₂

На основе первого свидетельства может быть определён диапазон, в котором находится вероятность, каждой из гипотез. В частности:

0.8 = Bel₁({Авто})  P({Авто})  Pl₁({Авто}) = 1.

При поступлении и учёте свидетельства 2 можно распространить доверия на основе вычисления ортогональных сумм. Промежуточные вычисления представим в виде таблицы

A=XY m₁(X) х m₂(Y)	m₂({ЖД})=0.5	m₂({Авто,ЖД})=0.2	m₂({})=0.3
m₁({Авто})=0.8	A= (0.4)	A={Авто} (0.16)	A={Авто} (0.24)
m₁({})=0.2	A={ЖД} (0.1)	A={Авто, ЖД} (0.04)	A={} (0.06)

Тогда вычислив

, можно будет определить значения ортогональные суммы базовых вероятностей

m₁ m₂ ({Авто}) =

= 0.6667

m₁ m₂ ({ЖД}) =

= 0.1666

m₁ m₂ ({Авто, ЖД}) =

= 0.0667

m₁ m₂ ({}) =

= 0.1

Все другие подмножества  имеют комбинированные доверия равные 0 и сумма всех комбинированных базовых вероятностей для m₁ m₂ равна 1. На основе этих базовых вероятностей могут быть вычислены доверия и правдоподобия для всех необходимых гипотез. С учётом распространения доверия на основе двух, полученных от экспертов свидетельств получим P({Авто})  Bel({Авто})=0.6667. Это говорит о том, что вновь поступившее свидетельство (свидетельство 2) снижает наше доверие к использованию к использованию для транспортировки автотранспорта.

Blog