40гг первые цифровые компьютеры программирование путем коммутации проводов
| Вид материала | Документы |
- Рабочая программа учебной дисциплины «Системы коммутации» Направление подготовки, 204.68kb.
- Неоднородный полупроводниковый носитель информации в переменном магнитном поле, 107.68kb.
- Темы Лекции Практика, 13.65kb.
- Общие принципы построения вычислительных сетей, 1480.56kb.
- Курс лекций "интернет технологии", 1261.62kb.
- А) Представление информации в цифровых автоматах (ЦА), 34.28kb.
- Информатика. Лекции. Краткая история компьютерной техники Первые компьютеры: Z3, Colossus,, 3630.67kb.
- Курс лекций для студентов очного и заочного отделений по специальности 210406 «Сети, 3045.9kb.
- Радумльская средняя школа, 28.4kb.
- Лекция №7. Обобщенная задача коммутации Важной задачей построения сетей ЭВМ является, 67.2kb.
Программа на языке Пролог представляет собой набор фактов и (возможно) правил.
?- 5+4<3.
No
Пролог анализирует запрос и выдает ответ Yes (Да) в случае истинности утверждения и No (Нет) в противном случае или когда ответ не может быть найден.
Хранение программ
- Хранят программы на языке Пролог в текстовых файлах, чаще всего имеющих расширение pl, например, example1.pl.
- Для того чтобы Пролог мог оперировать информацией, содержащейся в файле, он должен ознакомится с его содержимым (проконсультироваться с ним).
?- [example1].
или
?- consult(example1).
Термы и объекты
- Программа на языке Пролог обычно описывает некую действительность.
- Объекты (элементы) описываемого мира представляются с помощью термов.
- Терм интуитивно означает объект.
- Существует 4 вида термов: атомы, числа, переменные и составные термы.
- Атомы и числа иногда группируют вместе и называют простейшими термами.
Атом
- Атом -это отдельный объект, считающийся элементарным.
- В Прологе атом представляется последовательностью букв нижнего и верхнего регистра, цифр и символа подчеркивания '_', начинающейся со строчной буквы.
- Любой набор допустимых символов, заключенный в апострофы является атомом.
- Комбинации специальных символов + - * = < > : & также являются атомами
Числа
- Целые (Integer)
- Вещественные (Float)
Переменные
- Переменными в Прологе являются строки символов, цифр и символа подчеркивания, начинающиеся с заглавной буквы или символа подчеркивания
X, _4711, X_1_2, Результат, _x23, Объект2
Анонимная переменная
- Анонимная переменная (обозначается одним символом подчеркивания) применяется, когда ее значение не используется в программе.
Составные термы (функции)
- Составные термы (функции) состоят из имени функции (нечислового атома) и списка аргументов (термов Пролога, то есть атомов, чисел, переменных или других составных термов), заключенных в круглые скобки и разделенных запятыми.
- Группы составных термов используют для составления фраз Пролога.
итого(клиент(X,23,_), 71)
'Что случилось?'(ничего)
Факты
- Программировать на Прологе - значит описывать некий мир.
- Программа на этом языке состоит из множества фраз, задающих взаимосвязь между термами.
- Каждый терм обозначает ту или иную сущность, принадлежащую миру. Один из способов описания - это задание фактов.
Факт
- Факт - это утверждение о том, что соблюдается некоторое конкретное отношение. Он является безусловно верным. В разговорной речи под фактом понимается нечто вроде "Сегодня солнечно" или “Коле 10 лет". На Прологе это запишется в виде
'Сегодня солнечно'.
'Коле 10 лет'.
Предикат
- Предикат - это логическая функция от одного или нескольких аргументов, то есть функция, действующая в множество из двух значений: истина и ложь. Предикат Пролога записывается в виде составного терма: имя_предиката(аргументы).
Аргументы предикатов
- Аргументы перечисляются через запятую и представляют собой какие-то объекты или свойства объектов, а имя предиката обозначает связь или отношение между аргументами.
- Предикат однозначно определяется парой: имя и количество аргументов.
Пример
Факт "Коля работает слесарем" на Прологе запишется следующим образом:
профессия(коля, слесарь).
База данных
- База данных на Прологе - это совокупность фактов.
- В процессе работы в базу данных можно добавлять новые факты, удалять или изменять старые.
Пример
Составим базу данных из следующих фактов: "слон больше, чем лошадь", "лошадь больше, чем осел", "осел больше, чем собака" и "осел больше, чем обезьяна":
больше(слон, лошадь).
больше(лошадь, осел).
больше(осел, собака).
больше(осел, обезьяна).
Запросы к базе данных
Запрос - это последовательность предикатов, разделенных запятыми и завершающаяся точкой.
- На естественном языке запятая соответствует союзу "и", а на языке математической логики обозначает конъюнкцию.
- С помощью запросов можно "спрашивать" базу данных о том, какие утверждения являются истинными.
- Предикат запроса называется целью.
Примеры запросов
?- 5+4<3.
No
?- больше(слон, лошадь).
Yes
?- больше(лошадь, слон).
No
?- больше(лошадь, корова).
No
Правила
- Правило задает новый предикат через определенные ранее.
- Правило состоит из головы (предиката) и тела (последовательности предикатов, разделенных запятыми). Голова и тело разделены знаком :-
- Правило должно заканчиваться точкой.
- Запятая в теле правила означает конъюнкцию (&&, логическое и).
Правила
- Знак :- есть схематическая запись стрелки (<-) и показывает, что из правой части следует левая. Этот знак читается как "если".
- Интуитивный смысл правила состоит в том, что цель, являющаяся головой, будет истинной, если Пролог сможет показать, что все выражения (подцели) в теле правила являются истинными.
Пример
Правило, определяющее отношение ребенок/2 через отношение отец/2, запишется следующим образом:
ребенок(X, Y) :- отец(Y, X).
Это означает, что если человек Y является для человека X отцом, то X является ребенком Y. Здесь X и Y - переменные.
Правила с рекурсией
- Т.к. в Прологе отсутствуют операторы управления, то более сложные правила создаются с помощью рекурсии.
- В Прологе рекурсия встречается, когда предикат содержит цель, которая ссылается на саму себя.
- В рекурсивном правиле более сложные входные аргументы должны выражаться через менее сложные.
- Используя рекурсию как прием программирования мы должны быть уверены, что рекурсивная процедура будет завершена.
Пример рекурсии
больше(слон, лошадь).
больше(лошадь, осел).
больше(осел, собака).
больше(осел, обезьяна).
больше_2(X, Y) :- больше(X, Y).
больше_2(X, Y) :- больше(X, Z), больше_2(Z, Y).
Результат использования рекурсивных правил
?- больше(слон, обезьяна).
No
?- больше_2(слон, обезьяна).
Yes
Функциональное программирование
(пример - Excel)
- Функциональное программирование ставит своей целью придать каждой программе простую математическую интерпретацию.
- Эта интерпретация должна быть независима от деталей исполнения.
Семантика ЯП
Семантика ЯП задается определением средств описания данных и действий.
Функциональное программирование использует математическое понятие функции для выражения концепции действия.
Подобно обычным математическим функциям, процедуры («функции») функциональных языков отображают одни объекты (аргументы) в другие (значения).
В отличие от процедур (функций) императивных языков, значения функций однозначно определяются их аргументами и не зависят от истории вычислительного процесса.
Важное различие между математическими функциями и императивными процедурами заключается в том, что процедуры должны быть эффективно определены.
Понятие функции используется в функциональных языках программирования и для выражения концепции данных.
Функции в функциональных языках являются объектами «первого класса».
Элементы первого класса - это элементы с наименьшим количеством ограничений. Важные свойства таких первоклассных элементов:
- На них можно ссылаться посредством переменных.
- Их можно включать в структуры данных.
- Их можно передавать как параметры.
- Они могут быть возвращены в качестве результата.
Язык Лисп
- Лисп – интерпретатор
- Обычно работа с интерпретатором Лиспа происходит по следующему сценарию:
- Пользователь вводит выражение.
- Интерпретатор вычисляет значение этого выражения и печатает результат.
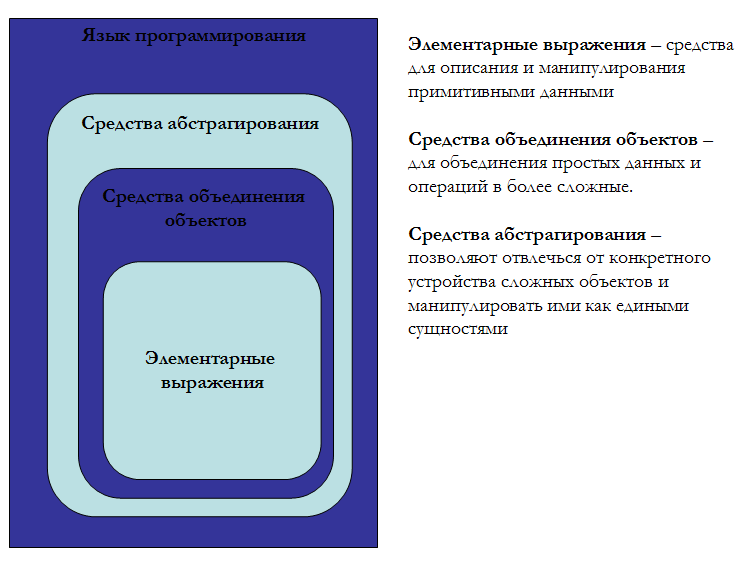
Элементарные выражения
Выражения и значения выражений.
Числовые константы обозначают числа, которые и являются их значениями. Разнообразие доступных типов чисел зависит от реализации языка, но все реализации поддерживают целые и вещественные числа, а многие ещё и рациональные и комплексные.
10
10
Последовательность букв, цифр и специальных знаков, отличающаяся от числа называется символом. Главное их назначение - именовать объекты. Поэтому, значением символа является объект, поименованный этим символом.
Hello
Error: undefined variable
С именем «+» связана встроенная функция, вычисляющая сумму чисел, которая и является значением.
+
#
Значением выражения '<символ> является сам этот символ. Лисп нечувствителен к регистру букв и значение символа приведено к стандартному виду.
'Hello
hello
Строковые константы записываются в двойных кавычках и представляют последовательности отображаемых знаков.
"Hello"
"Hello"
Две логические константы #t и #f обозначают истину и ложь.
#f
#f
Константы и символы носят общее имя атомы, поскольку представляют собой простейшие элементы языка, из которых строятся выражения.
Для записи выражений (форм в терминологии Лиспа) используется единая префиксная форма: имя функции стоит перед аргументами и записывается внутри скобок
(+ 2 2)
4
(* 1.1 2)
2.2
(= 1 2)
#f
Подобные выражения, описывающие применение функции к аргументам, называются комбинационными формами или комбинациями.
Значение комбинации - результат применения функции, указанной первым элементом списка (оператором) к параметрам, которые являются значениями остальных элементов (операндов).
В данном случае, операторы - встроенные функции +,*,=.
Пример более сложного выражения.
(+ (* 3 5) (- 10 5))
20
Общее правило вычисления значения комбинации следующее:
- Вычислить значение всех подвыражений.
2. Применить функцию, которая является значением оператора к аргументам, которые являются значениями операндов.
Таким образом, в Лиспе используется аппликативный порядок вычислений
В традиционной математической нотации имя функции стоит перед аргументами, заключенными в скобках. Кроме того, используется инфиксная запись арифметических выражений, разнообразные индексы и специальные знаки.
| Математическая запись | Запись на Лиспе |
| f(x) | (f x) |
| g(x, y) | (g x y) |
| h(x, g(y, z )) | (h x (g y z)) |
| sin x | (sin x) |
| x + y | (+ x z) |
| x + y·z | (+ x (* y z)) |
| xy | (expt x y) |
| |x| | (abs x) |
| x = y | (= x y) |
| x + y < z | (< (+ x y) z) |
В сравнении с этим многообразием и даже с синтаксисом большинства языков программирования префиксная форма кажется несколько непривычной и громоздкой. Но она обладает, по крайней мере, одним неоспоримым достоинством - описание синтаксиса умещается на одной строчке:
<выражение> ::= <атом> | ( <выражение>)
Чтобы сделать выражения более читаемыми, многие реализации допускают использование квадратных скобок.
(/ [+ (* 3 5) (- 10 5)] 2)
10
Несмотря на то, что Лисп - бестиповый язык и любое сочетание аргументов является синтаксически допустимым, в процессе выполнения для каждого значения определяется его тип и попытка применить + к логическому значению вызывает ошибку.
Поэтому Лисп называют динамически типизированным языком.
Заметим что правила типизации соблюдаются гораздо более строго, чем в Си или даже в Паскале - нет никакой возможности подсунуть функции аргумент не того типа.
(1 2 3)
Error: attempt to apply a non-procedure
1 не является функцией. Поэтому попытка применить её приводит к ошибке.
(+ 1 (= 1 2))
Error in +: #f is not a number.
Базовые функции.
В Лиспе определён большой набор базовых функций, рассмотрим некоторые из них. Это во-первых арифметические операции (+,-,*,/). Функции + и * имеют произвольное количество аргументов. В принципе, это не очень хорошая практика, но в данном случае она себя оправдывает.
| (+ 1 2 3 4 5) 15 | (+ 1) 1 | (* 1 2 3 4 5) 120 |
Поскольку операции вычитания и деления не ассоциативны, попытка расширить их определение на произвольное количество аргументов может привести к путанице. Однако, для одного аргумента определено, что (- a)выдаёт -a , а (/ a)- 1/a.
| (- 5) -5 | (/ 10 5) 2 | (/ 2 3) 2/3 |
Неожиданность. Ожидалось скорее 0 или 0.666667 в зависимости от типа данных. Но для непредубежденного человека вполне естественно. Впрочем, если реализация не поддерживает рациональных чисел (что допускается для Scheme) получим 0.666667.
Для деления с остатком предназначены функции quotient и remainder, возвращающие целую часть и остаток от деления.
Логические функции
Функции, возвращающие логические значения, называются предикатами. В Lisp принято названия предикатов (кроме распространённых арифметических операций сравнения =,>,<,<=,>= ) завершать вопросительным знаком или - буквой "p"(от слова predicate).
| (= 1 2) #f | (odd? 2) #f |
| (< 1 2) #t | even? 2) #t |
(Подобно + и *, операции сравнения допускают произвольное число аргументов (но, конечно же, не менее двух). Это сделано всё с той же целью - уменьшить сложность выражений. Например (< x1 x2 …xn)вернёт #t, только если аргументы упорядочены по возрастанию.
Для символов единственная осмысленная операция - сравнение на идентичность.
(eq? 'a 'a)
#t
Может показаться странным использование специального предиката, а не символа равенства. Но мы часто подразумеваем совершенно разные вещи, когда говорим, что два объекта равны. Предикат = сравнивает численные значения двух выражений, а предикат eq? проверяет, что эти выражения именуют один и тот же объект. Поэтому:
| (= 1 1.0) #t | (eq? 1 1.0) #f | (eq? 1 1) #t |
Типовые предикаты
Поскольку переменные Лиспа могут принимать значение любого типа, необходимо иметь возможность определять этот тип. Для этого предусмотрены типовые предикаты.
| (boolean? 1) #f | (integer? 1) #t | (real? 1.1) #t | (procedure? '+) #f |
| (number? 1) #t | (integer? 1.1) #f | (procedure? +) #t | (symbol? '+) #t |
Логические связки
Для представления логических связок используются функции not, or и and.
(not x)
возвращает #t, если значение аргумента равно #f и #f в противном случае.
(or x1 x2 … xn)
возвращает значение первого аргумента, не равного #f. Если же все аргументы имеют значение #f, то оно и возвращается.
(and x1 x2 … xn)
возвращает значение #f, если оно встречается среди значений аргументов. В противном случае возвращается значение последнего аргумента.
Любое значение, отличное от #f интерпретируется как истина.
| (not #f) #t | (  not 0) not 0)#f |
Условные выражения
Если зависимость значений истинности от значений других типов выражается предикатами, а зависимость значений истинности от других значениях истинности логическими связками, то условные выражения - средство для выражения зависимости значений произвольного типа от значений истинности.
(if p et ef)
возвращает значение ef, если значение p - #f , и et в противном случае.
(cond (p1 e1) (p2 e2) … (pn en))
возвращает значение ei , для первого i при котором значение pi отлично от #f.
Средства объединения объектов
Определения
Для определения новых объектов, применяются определяющие формы.
(define n e)
связывает имя n со значением выражения e.
(define (f a1…an) e)
определяет новую функцию с именем f.
a1…an - формальные параметры, т.е. имена, используемые внутри тела функции для ссылок на соответствующие параметры.
e -тело функции, выражение, определяющее её значение
| (define x 1) x 1 (+ x x) 2 | (define x 2) (+ x x) 4 |
