Законам механики

Вид материала

Подобный материал:

Кинематика

При наблюдении множества движений тел в пространстве можно заметить их общее свойство: в любом из этих процессов изменяется положение одних тел (или частей тела) относительно других.

Изменение положения одного тела относительно другого называют механическим движением. Раздел физики, изучающий механические движения, называется механикой.

Любое изменение тел в природе подчиняется определенным законам. Движение тел в пространстве подчиняется законам механики.

Раздел механики, изучающий способы описания движений и связь между величинами, которые характеризуют эти движения, называют кинематикой. (В следующем разделе механики, в динамике, будут рассмотрены причины изменения параметров механического движения тел.)

Любое механическое движение является относительным. Тело, относительно которого наблюдается движение, называют телом отсчета.

Положение тела относительно тела отсчета можно охарактеризовать с помощью системы координат, которую следует жестко связать с телом отсчета. Кроме того, следует договориться о том, как будет отсчитываться время движения. С этой целью необходимо условиться о начале измерения времени и способе его отсчета.

Тело отсчета, связанная с ним система координат и способ измерения времени движения с указанием на начало его отсчета образуют систему отсчета.

Без указания системы отсчета разговор о движении является бессмысленным. Например, движение пассажира в поезде неопределенно без указания системы отсчета.

Движение тел может быть очень сложным. При этом важное значение имеет строение самого тела: при движении отдельные его части могут перемещаться относительно друг друга (например, движение ракеты и ее отделившейся ступени), что также усложняет движение.

Как уже было сказано, в науке принято теоретическое описание явления строить на основе модели, которая отражает изучаемый объект с той или иной степенью точности.

Каждая модель лишь приближенно отражает свойства изучаемого объекта. Самой простой моделью механики, с помощью которой можно описать движение тел в пространстве, следует считать материальную точку. За материальную точку принимается такое тело, размерами которого можно пренебречь при решении поставленных задач. Такое допущение возможно в следующих случаях:

а) если размеры тела пренебрежимо малы по сравнению с его перемещением;
б) если все точки тела совершают одинаковые движения (такое движение тела называют поступательным);
в) если вращательным движением отдельных частей можно пренебречь.

Линия, по которой движется материальная точка в данной системе отсчета, называется траекторией.

В кинематике под движением точки подразумевается ее перемещение в пространстве относительно тела отсчета и связанной с ним системы координат. Следовательно, в кинематике описание движения носит геометрический характер.

При решении задач по кинематике удобнее выбирать ту систему, в которой движение выглядит проще. Так, например, движение материальной точки в плоскости Земли может быть описано двумя координатами, а движение точки вдоль определенной дороги - одной координатой. Если же материальная точка перемещается в пространстве и при этом изменяются все три координаты, то следует воспользоваться трехмерной системой координат.

Как известно из геометрии, положение точки в пространстве и его изменение можно описать двумя способами:

Один из них требует введения понятия "радиус-вектор". Радиусом-вектором (r) называется направленный отрезок, соединяющий начало координат и точку с произвольными координатами. Положение точки в пространстве в заданной системе отсчета будет полностью определено, если известен r (его положение относительно осей координат и его размеры) (рис. 1).
Второй способ описания местоположения точки связан с первым: точка может быть задана с помощью трех координат, которые в данном случае равны проекциям вектора на оси Ox; Oy; Oz (проекция вектора r на ось Ох обозначается r_х, на ось Оу - r_у, на ось Oz - r_z). Следует отличать проекции вектора от составляющих вектора.

Первый способ предполагает, что любое изменение положения точки должно описываться как результат сложения радиуса-вектора с его изменением (приращением). Этот способ связан с достаточно трудоемкой операцией сложения векторов по правилу параллелограмма.

Второй способ приводит к сложению алгебраических величин - координат, что является более привычной операцией.

Таким образом, оба способа описания положения точки в пространстве однозначно связаны между собой, но в школьном курсе при решении задач предпочтение отдается координатному методу (хотя есть ряд задач повышенной трудности, решить которые можно только с помощью векторного подхода).

Заметим, что Государственным стандартом введены следующие обозначения:

r - векторная величина (в данном случае радиус-вектор);
|r| - ее модуль;
r_х - проекция вектора r на ось х.

При этом нетрудно доказать, что модуль вектора будет равен

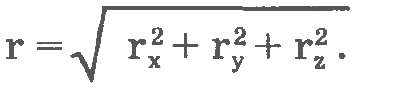
Рассмотрим, как меняется радиус-вектор при движении точки в пространстве.

Пусть в момент времени t₀ = 0 точка А имеет координаты х₀, у₀, z₀, (что соответственно описывается радиусом-вектором r₀), а по истечении некоторого промежутка времени t₁ материальная точка переместилась в точку В, ее координаты стали равными x₁, у₁, z₁ (что соответственно описывается радиусом-вектором r₁) (рис. 2).

Для того чтобы рассчитать, как изменилась величина, необходимо вычесть из ее нового значения предыдущее, то есть дельта r = r₁ - r₀ . Эту величину называют перемещением. Нетрудно заметить, что для координат это изменение можно записать следующим образом:

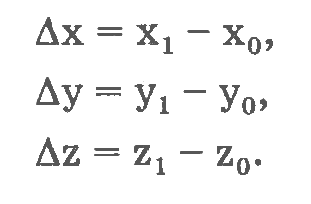
Отсюда следует:

Следовательно, для того чтобы определить местоположение точки через какой-то промежуток времени t₁, необходимо знать начальный радиус-вектор и перемещение за промежуток времени t₁. Эта же задача может быть решена, если известны начальные координаты и их приращение за промежуток времени t₁

Очень важно отметить, что перемещение чаще всего не совпадает с траекторией, поэтому модуль перемещения отличается от пройденного пути (за исключением того случая, когда траектория точки есть прямая линия) (см. рис. 2).

Перемещение показывает, на какое расстояние и в каком направлении точка сместилась при своем движении. Однако эта величина не позволяет оценить характер движения. Для этого необходимо ввести еще одну величину, характеризующую быстроту движения. Такой величиной является средняя скорость (v_ср), которая показывает, как быстро в среднем перемещалась точка:

где v_ср - средняя скорость; дельта r- перемещение; дельта t - промежуток времени, за который перемещение произошло.

В Международной системе единиц (СИ) модуль скорости измеряется в м/с. В практике применяются и другие единицы: км/ч; см/с и т. д.

Знания средней скорости недостаточно для подробного описания движения. Средняя скорость позволяет тем точнее описывать процесс движения, чем за меньший промежуток времени рассматривается перемещение точки.

При стремлении дельта t к нулю дробь дельта r/ дельта t будет стремиться к некоторому значению средней скорости, характеризующему движение материальной точки, вблизи которой был взят малый интервал времени дельта t и соответственно малое изменение вектора перемещения дельта r.

Это значение, т. е. предел, к которому стремится дробь дельта r/ дельта t при стремлении дельта t к нулю, называют мгновенной скоростью в данной точке или в данный момент времени и обозначают v:

Так как дельта t - скалярная величина, то направление скорости совпадает с направлением вектора перемещения. Если дельта r стремится к нулю, то нетрудно увидеть, что направление мгновенной скорости в точке траектории совпадает с касательной (рис. 3).

Итак, вектор v скорости точки направлен по касательной к траектории точки в сторону ее перемещения. Модуль вектора скорости v характеризует быстроту перемещения точки по траектории.

Прибор, которым измеряют скорость, называется спидометром.

Любой вектор можно разложить на его составляющие, при этом следует выполнить требование: векторная сумма составляющих вектора должна быть равна вектору, который подлежал разложению.

На рис. 4, а и б изображены векторы и их составляющие. Напомним, что проекция вектора на ось - алгебраическая величина, численно равна произведению модуля вектора на косинус угла между вектором и осью (при этом в трехмерном пространстве рассматривается угол между плоскостью, которая проходит через вектор, и интересующей нас осью). Рассмотрим пример в двухмерном пространстве: если вектор r расположен на плоскости хОу, то его проекция на ось Ох равна r_x = r*cosa (рис. 5).

Вектор скорости с течением времени может изменяться: либо его модуль, либо направление, либо то и другое. Для характеристики быстроты изменения скорости движущейся точки вводится понятие ускорения. Ускорение (а) - векторная величина. Оно равно отношению изменения скорости к промежутку времени, за которое это изменение произошло:

Если выбирать все меньшие и меньшие промежутки времени, то а_ср будет более точно описывать характер изменения скорости точки, и в пределе можно получить мгновенное ускорение точки, которое будет направлено туда же, куда направлен вектор изменения скорости дельта v.

Отметим, что ускорение направлено в сторону изменения скорости, но не в сторону самой скорости. Например, при движении брошенного вверх тела скорость направлена вверх, но она убывает, при этом изменение скорости направлено вниз. Следовательно, и ускорение направлено в этом случае вниз. Оно носит название ускорения свободного падения (обозначение g).

Ускорение измеряется в Международной системе единиц (СИ) в 1 м/с². Физический смысл единицы ускорения: 1 м/с² - это такое ускорение, при котором за 1 с скорость изменяется на 1 м/с при условии, что ускорение в этот промежуток времени остается постоянным.

Ускорение измеряется прибором, который называется акселерометром.

Blog

Законам механики