Занятие №1. Механическое движение и его относительность. Законы Ньютона. Закон всемирного тяготения. Механическим движением

Вид материала

Закон

Содержание Материальной точкой Равномерное движение. Принцип относительности галилея Задача №2. Задача №1. Домашнее задание. Закон всемирного тяготения Задача №1. Мпульс тела. Механическая работа Мощность (Р)– Энергия– скалярная функция состояния, имеющая размерность работы и сохраняющаяся для замкнутых систем. Механическая энергия– Кинетическая энергия– Потенциальная энергия упруго- деформированного тела Задача №2. Домашнее задание. Механические колебания Свободные колебания Атухание колебаний Амплитуда колебаний (а) ... Полное содержание

Подобный материал:

• Самостоятельная работа Повторение основных понятий, определений, законов из курса механики, 251.69kb.
• Урок по физике в 9 классе Тема урока: закон всемирного тяготения, 114.37kb.
• Урок по теме «Закон всемирного тяготения», 42.5kb.
• А. А. Гришаев этот «цифровой» физический мир в 5-ти разделах с Дополнением Раздел организация, 975.13kb.
• Программа вступительного испытания по дисциплине Физика, 54.3kb.
• Физика механика кинематика, 60.32kb.
• Примерные программы вступительных испытаний в высшие учебные заведения российской федерации, 47.51kb.
• Программа по физике механика, 42.61kb.
• Связанные с механическим движением жидкости в различных природных и техногенных условиях, 1539.22kb.
•  - высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз,, 99.34kb.

Занятие №1.

Механическое движение и его относительность. Законы Ньютона. Закон всемирного тяготения.

Механическим движением называется изменение положения тела (или его частей) относительно других тел.

Кинематикой называется раздел механики, в котором изучаются механические движения тел во времени и не рассматриваются какие-либо воздействия на эти тела других тел или полей.

Тело отсчёта твердое тело, относительно которого определяется положение всех остальных тел.

Система отсчёта- совокупность тела отсчета, связанной с ним системы координат и часов.

Материальной точкой называется тело, размерами которого в данной задаче можно пренебречь.

Траектория- линия, вдоль которой движется тело.

Путь -скалярная величина, равная длине траектории. S[м]

Перемещение -радиус-вектор, соединяющий начальную и конечную точку пути. r [ м ]

Скорость -путь, пройденный телом за единицу времени. υ [м/с].

Равномерное движение. υ=const; S=υt

Равноускоренное движение.

Ускорение-это физическая величина, равная отношению изменения скорости материальной точки к длительности промежутка времени, в течение которого это изменение произошло.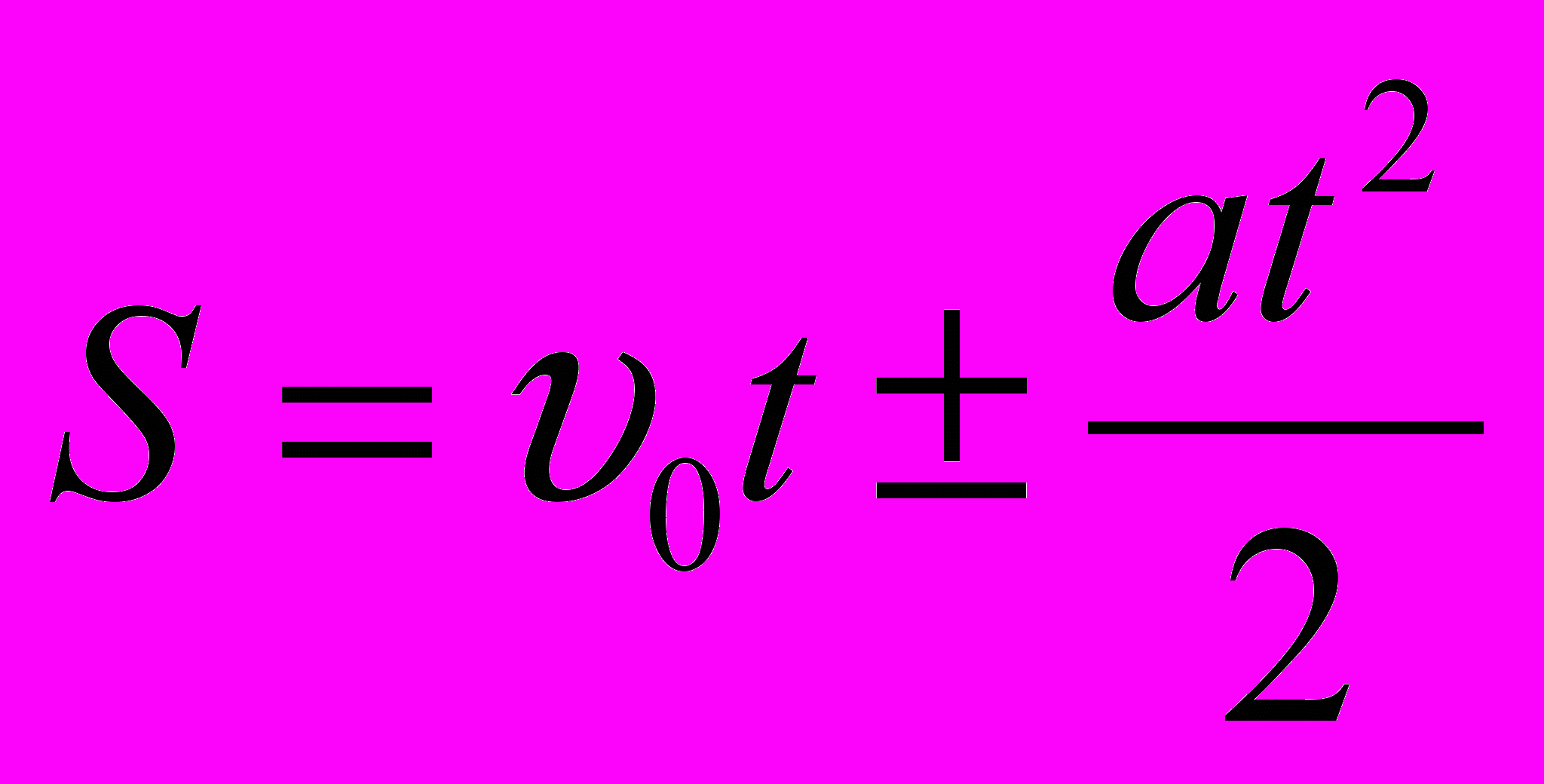

[м/с²].

П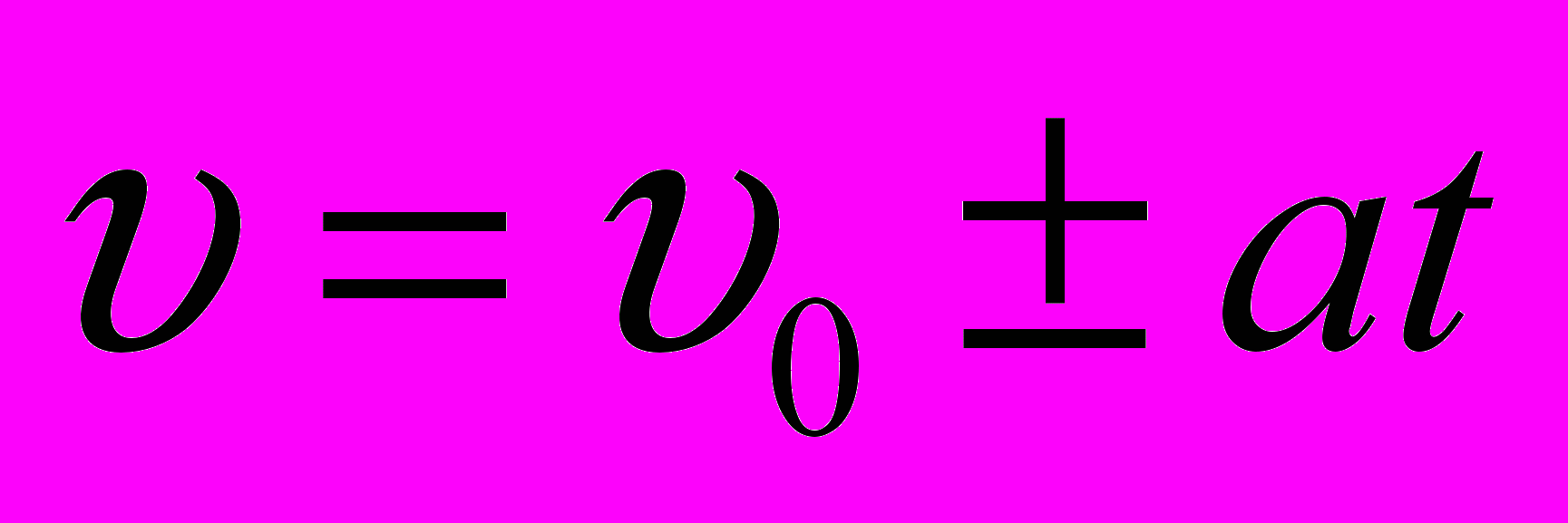уть «+» - когда тело разгоняется, «-» - когда тело тормозит.

Скорость

Свободное падение

ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ– законы классической механики для замкнутых систем во всех инерциальных системах отсчета имеют один и тот же вид.

Задача №1. С каким ускорением двигался автомобиль, если за 10 секунд его скорость увеличилась с 18 до 36 км/ч?

Задача №2. Какова величина (модуль) ускорения ударной части свайного молота, если её скорость при ударе о сваю уменьшается от 5 м/с до нуля за 0,05 с?


Законы Ньютона.

1 закон: Существуют такие системы отсчёта, в которых всякое тело будет сохранять состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие других тел не заставит его изменить это состояние.

2 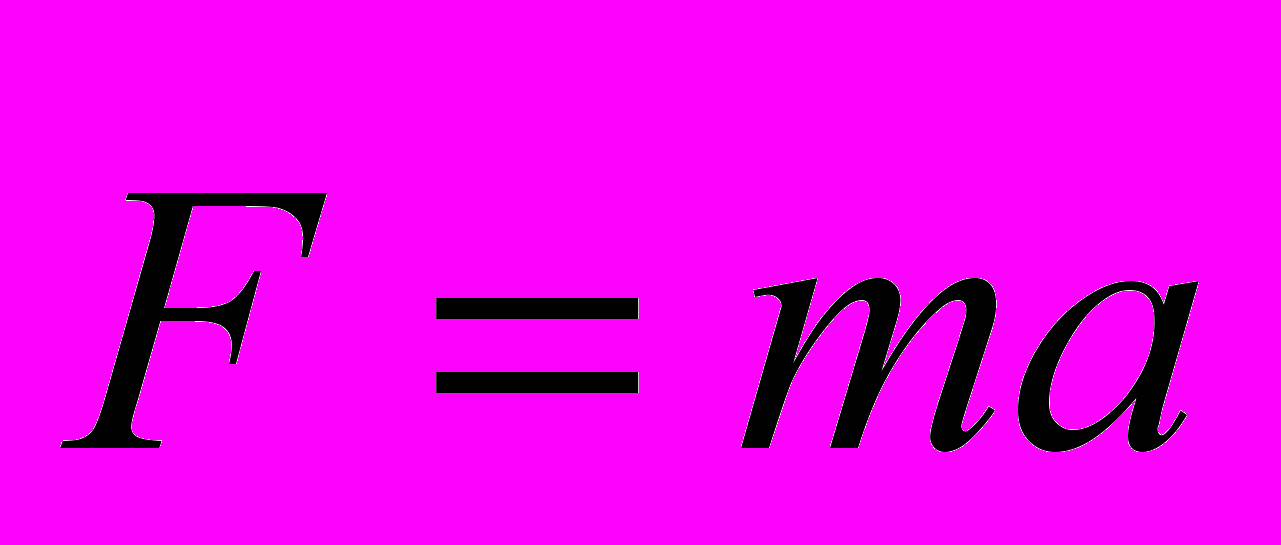закон: под действием силы тело приобретает такое ускорение, что его произведение на массу тела равно действующей силе.

3 закон: силы, с которыми взаимодействующие тела действуют друг на друга, равны по модулю и направлены по одной прямой в противоположные стороны.

Задача №1. Лыжник, начиная спуск с горы, имеет скорость 2м/с и в течение 20 с проезжает путь 150 м. Какой скорости он достигает в конце пути?

Задача №2.Тормозящий автомобиль движется с ускорением, модуль которого равен 2,5 м/с² и при этом скорость его уменьшается с 15 до 5 м/с. Какой путь прошёл автомобиль при торможении?

Домашнее задание. Выучить конспект. Решить задачу: №144. С каким ускорением двигался при разбеге реактивный самолёт массой 60 т, если сила тяги двигателей 90 кН


Закон всемирного тяготения.

ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ: сила гравитационного притяжения любых двух частиц (материальных точек) прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.



ВЕС ТЕЛА ( P  )– сила, с которой тело давит на горизонтальную опору или растягивает вертикальный подвес.

Измеряется с помощью весов. Единицей веса в СИ является ньютон (Н).

НЕВЕСОМОСТЬ– состояние тела, при котором его вес равен нулю (движение под действием только силы тяжести).

Задача №1.Определите силу взаимного тяготения двух кораблей, удалённых друг от друга на 100 м, если масса каждого из них 10 тысяч тонн. Корабли считать материальными точками.

Задача №2.Два тела массами по 5т притягиваются друг к другу с силой 6,7^. 10^-9 Н. На каком расстоянии друг от друга расположены эти тела?

Домашнее задание 1. Выучить формулу и формулировку закона всемирного тяготения.2.Решить задачу: №171. Найти силу гравитационного взаимодействия Земли и Луны. (Масса Земли: 6 ^. 10²⁴ кг, масса Луны:7,35 ^. 10²² кг, расстояние от Земли до Луны: 3,8 ^.10⁸ м).

Занятие №3

Закон сохранения импульса. Механическая работа и мощность. Закон сохранения энергии.

И 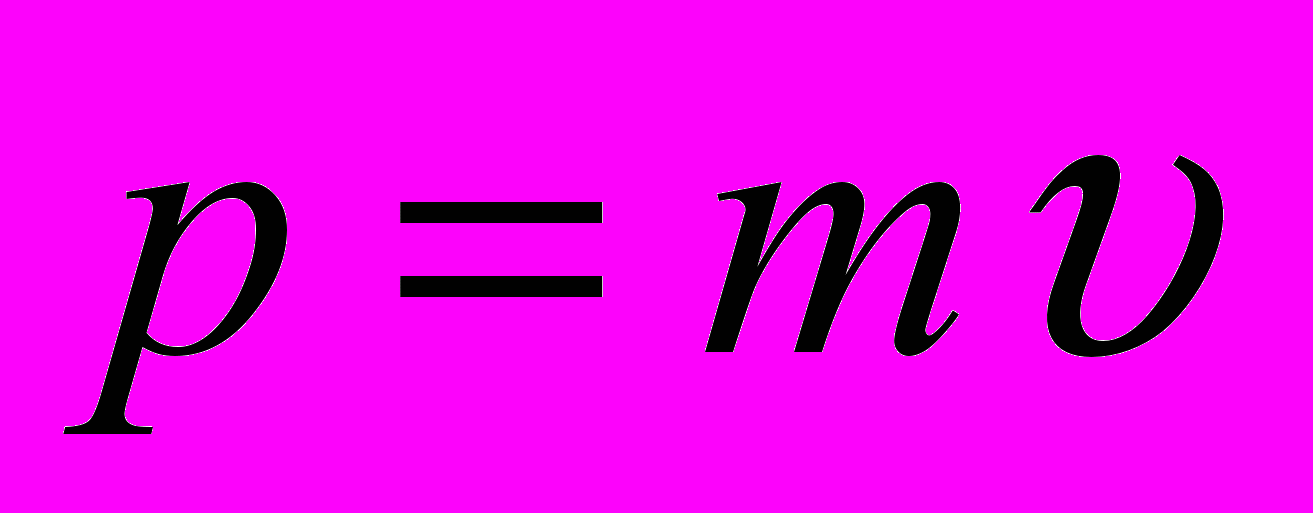МПУЛЬС ТЕЛА. Векторная физическая величина, равная произведению массы тела на его скорость. Единицей импульса в СИ является  кг·м/с.

Закон сохранения импульса. При любых процессах в замкнутой системе ее полный импульс остается неизменным.

М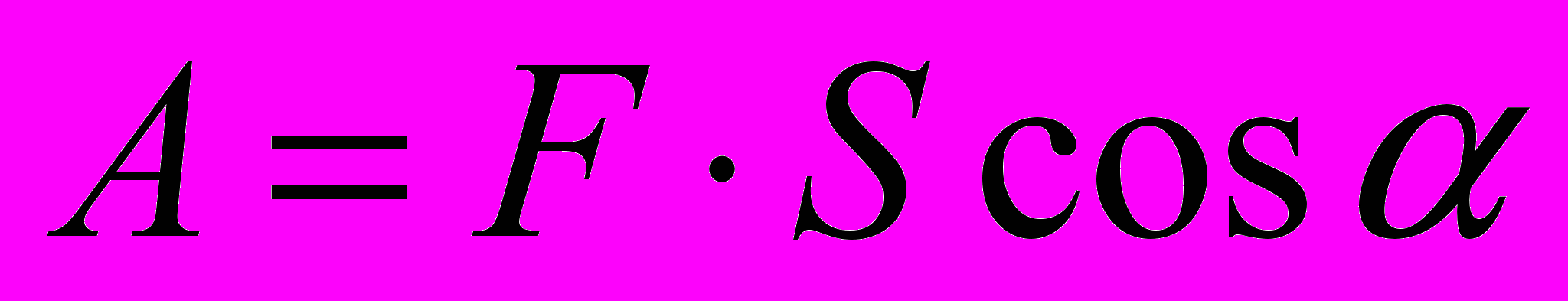еханическая работа (A)  – скалярная физическая величина, равная произведению модуля силы (F), модуля перемещения (S) и косинуса угла между направлениями силы и перемещения. Единицей работы в СИ является джоуль (Дж).

А- работа [Дж], F- сила [H], S- перемещение [м], - угол между F и S.

М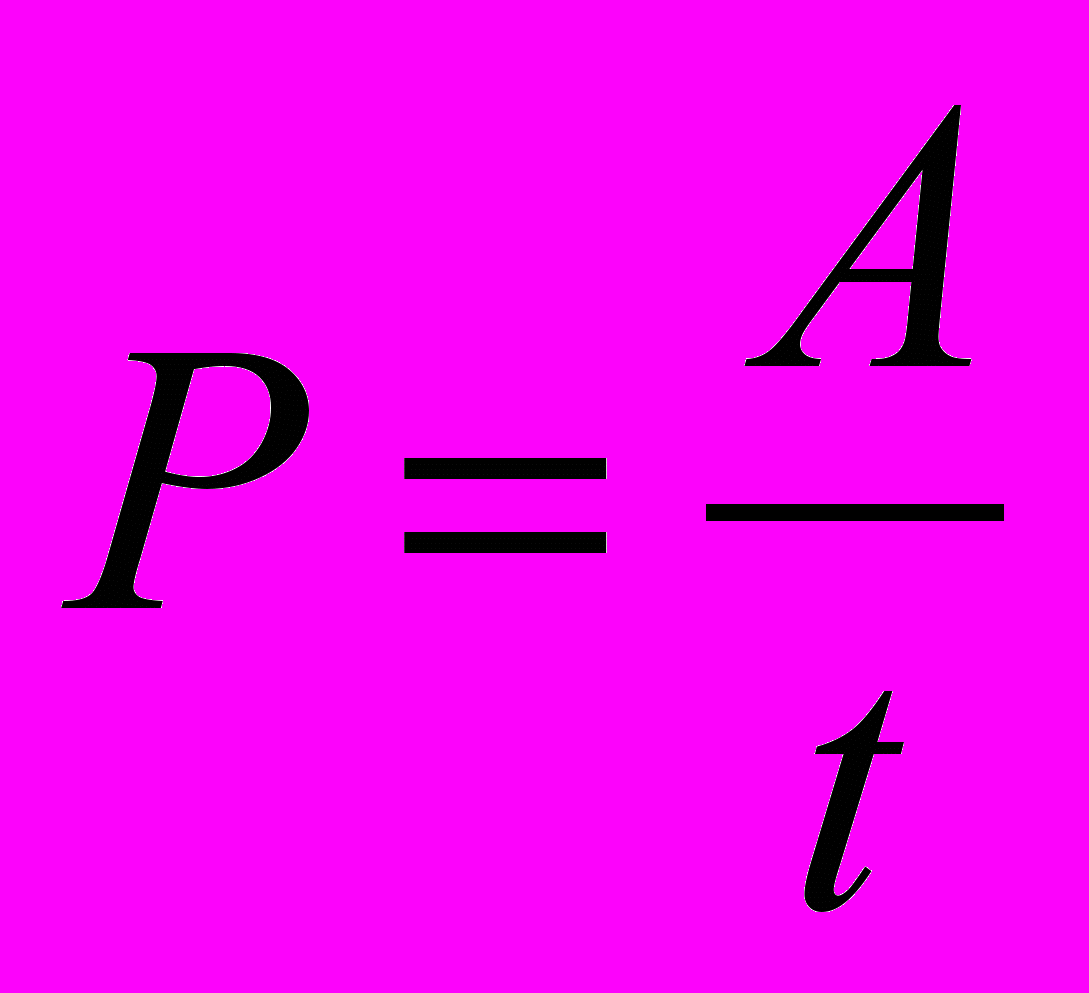ощность (Р)– скалярная физическая величина, равная отношению работы к промежутку времени, в течение которого она была произведена. Единицей мощности в СИ является ватт (Вт). Р- мощность [Вт], А- работа [Дж], t - время [c].

Энергия– скалярная функция состояния, имеющая размерность работы и сохраняющаяся для замкнутых систем.

Механическая энергия– скалярная физическая величина, равная сумме кинетической и потенциальной энергий.

К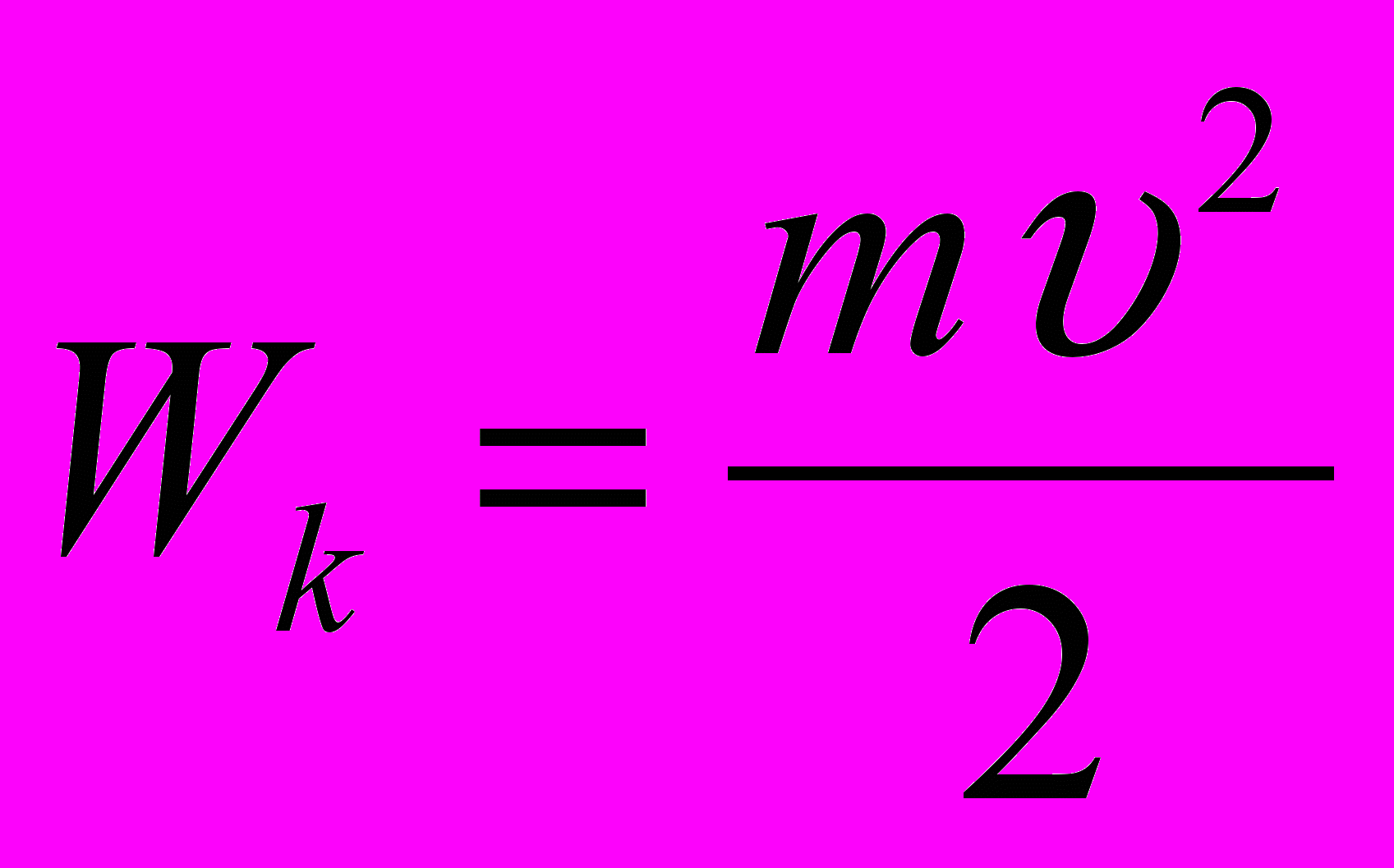инетическая энергия– скалярная физическая величина, характеризующая движущееся тело и равная половине произведения массы частицы на квадрат ее скорости.

Единицей кинетической энергии в СИ является джоуль (Дж).

П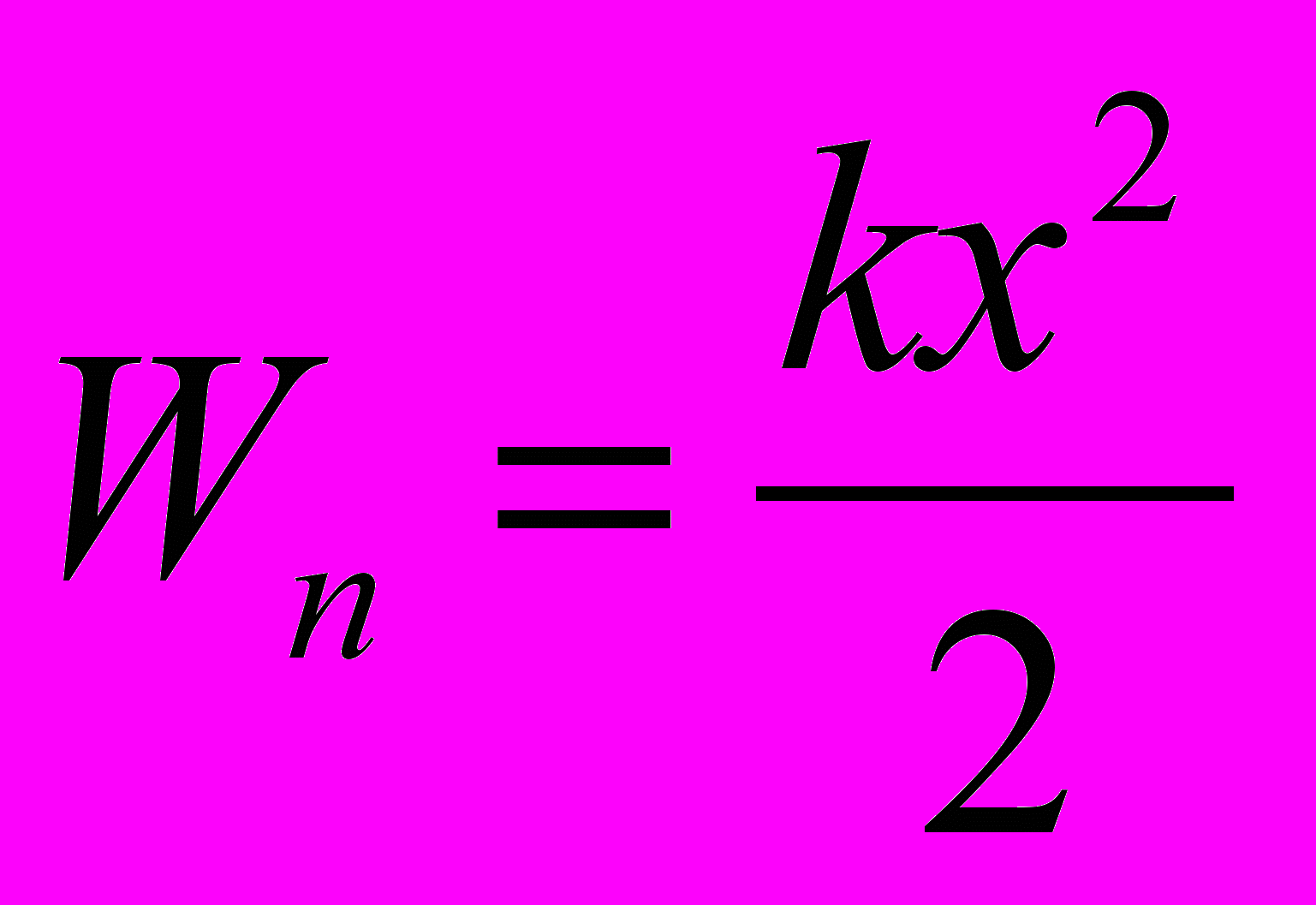отенциальная энергия– скалярная физическая величина, равная работе, совершаемой потенциальными силами при перемещении частицы из данного положения в нулевое (т. е. такое, в котором потенциальная энергия считается равной нулю).

Потенциальная энергия упруго- деформированного тела:

З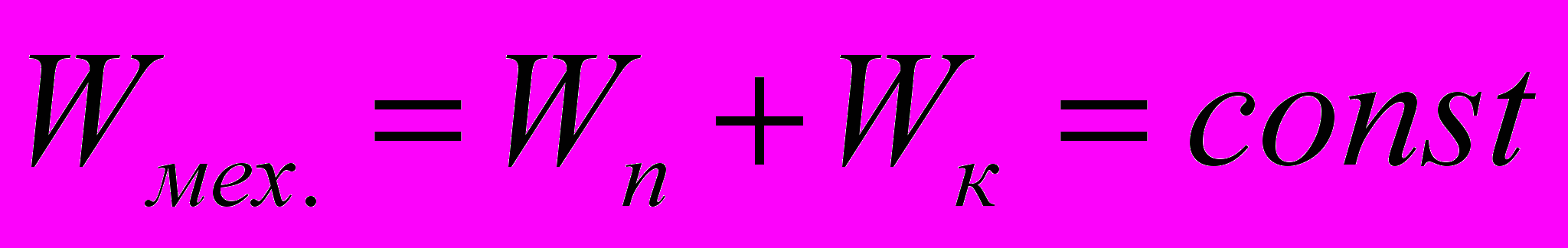акон сохранения механической энергии. При любых процессах, происходящих в консервативной системе, ее полная механическая энергия остается неизменной.

Задача №1. Автомобиль массой 1,2 т движется со скоростью 72 км/ч. Чему равна кинетическая энергия автомобиля? Ответ выразить в килоджоулях.

Задача №2. Тело массой 1 кг свободно падает с высоты 490 м. Чему равна его потенциальная энергия в начальный момент времени? Ответ выразить в килоджоулях (кДж).

Домашнее задание. Выучить конспект. Подготовиться т тесту по механике. Решить задачу № 360. Тело массой 3 кг, свободно падает с высоты 5 м. Найти потенциальную и кинетическую энергии тела на расстоянии 2 м от поверхности земли.

Занятие №4

Механические колебания. Распространение колебаний в среде. Волны и их характеристики.

КОЛЕБАНИЯ - процессы, обладающие той или иной степенью повторяемости во времени.

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ – повторяющиеся движения, при которых тело многократно и в разных направлениях проходит одно и то же (среднее) положение.

Различают периодические и непериодические колебания. Периодическими называют колебания, при которых состояние колеблющегося тела повторяется через равные промежутки времени.

СВОБОДНЫЕ КОЛЕБАНИЯ – колебания, возникающие в системе под действием внутренних сил после того, как система была выведена из состояния равновесия и предоставлена самой себе.

З АТУХАНИЕ КОЛЕБАНИЙ – уменьшение амплитуды колебаний системы с течением времени. В случае механических колебаний затухание обусловлено трением.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ – колебания, происходящие по законам синуса или косинуса:

x – значение колеблющейся величины в момент времени t, A – амплитуда колебаний, ω– циклическая (или круговая) частота, φ – полная фаза колебаний. Графиком гармонических колебаний является синусоида.

АМПЛИТУДА КОЛЕБАНИЙ (А) - максимальное значение периодически изменяющейся величины.

П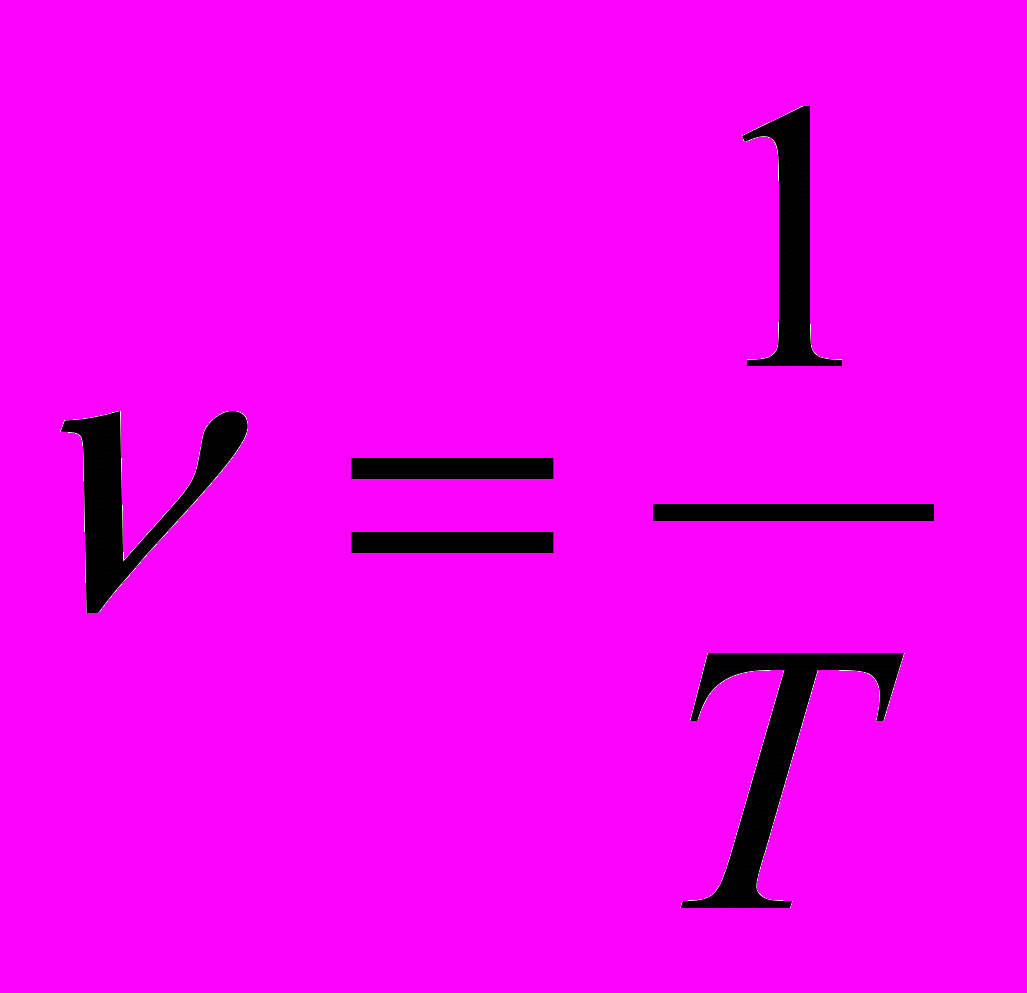ЕРИОД КОЛЕБАНИЙ (Т) – время, за которое совершается одно полное колебание. В СИ измеряется в секундах (c).

ЧАСТОТА колебаний (ν) – физическая величина, показывающая число колебаний, совершаемых за 1 с.

Частота ν является величиной, обратной периоду колебаний. Единицей частоты в СИ является герц (Гц).

Циклическая (или круговая) частота (ω) – это число колебаний, совершаемых за 2π секунд. Единицей циклической частоты в СИ является радиан в секунду (рад/с).

Ф 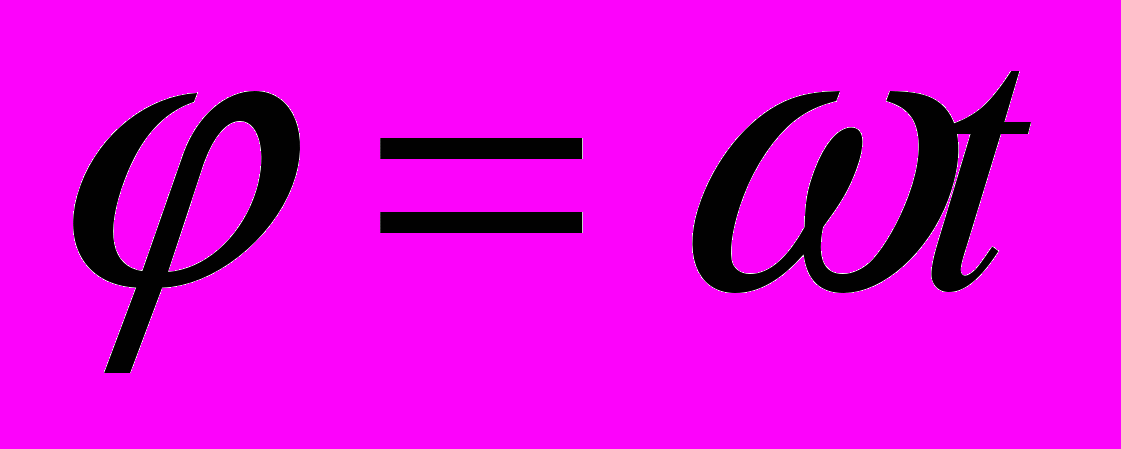АЗА КОЛЕБАНИЙ (φ) -определяет величину и направление периодически изменяющейся величины в данный момент времени.

М АТЕМАТИЧЕСКИЙ МАЯТНИК – колеблющаяся в поле тяжести материальная точка, подвешенная на невесомой и нерастяжимой нити.

Т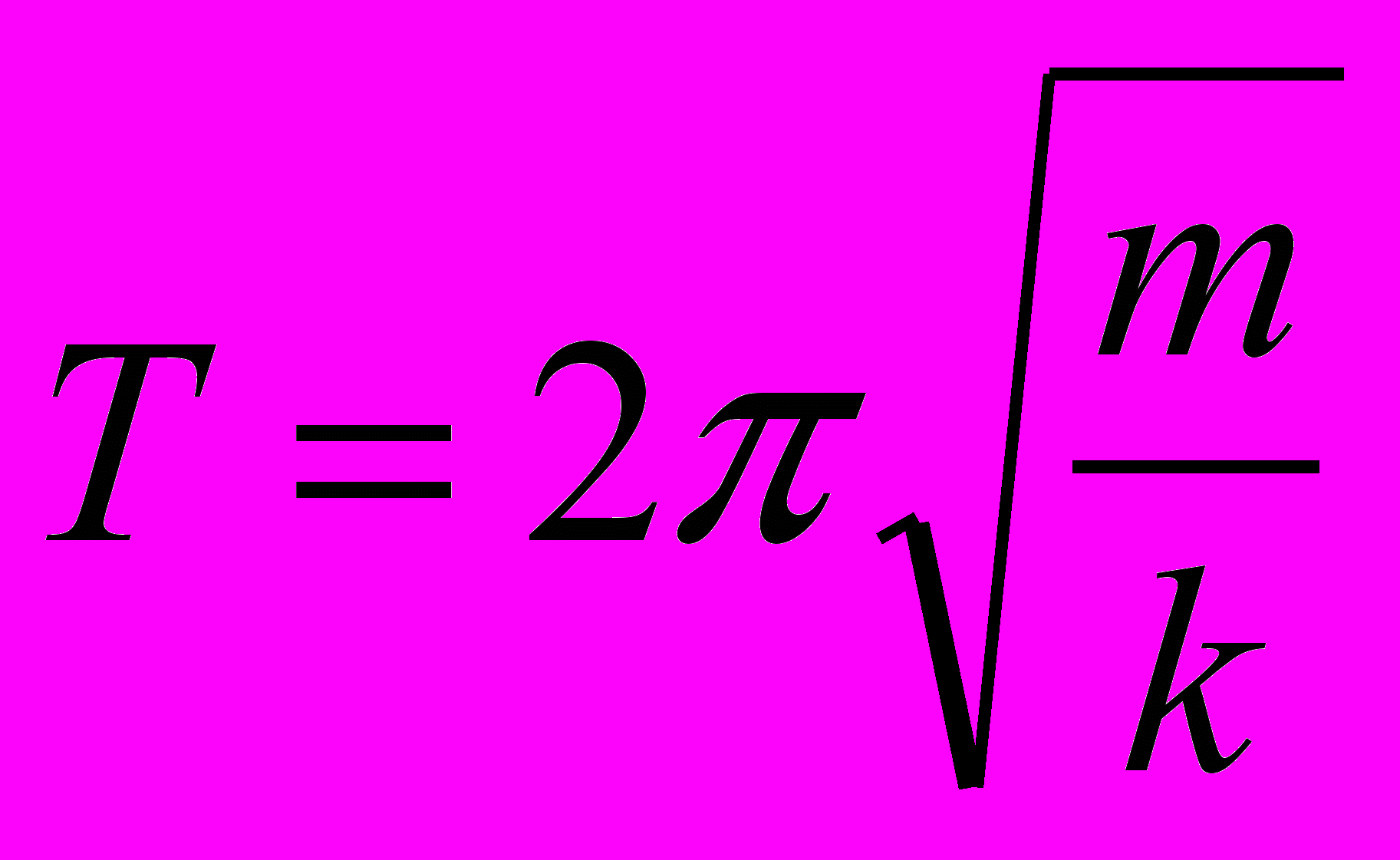- период (с); l- длина нити (м);g- ускорение свободного падения (м/с²).

ФИЗИЧЕСКИЙ МАЯТНИК – груз, колеблющийся на пружине.

Т- период (с); m- масса груза (кг); k- коэффициент упругости пружины (Н/м).

ВОЛНЫ –колебания, распространяющиеся в пространстве с течением времени. Наиболее важные и часто встречающиеся виды волн: упругие волны, волны на поверхности жидкости и электромагнитные волны. ВОЛНОВОЙ ФРОНТ- волновая поверхность, отделяющая в данный момент времени часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. При этом само распространение волны можно рассматривать как движение волнового фронта.

ДЛИНА ВОЛНЫ (λ) – расстояние, на которое распространяется волна за время, равное периоду колебаний в ней (расстояние между соседними гребнями волны). λ- длина волны (м); ν- скорость волны (м/с); Т- период (с). ПОПЕРЕЧНЫЕ ВОЛНЫ – волны, у которых характеризующие их векторные величины совершают колебания в направлении, перпендикулярном направлению распространения волны. ПРОДОЛЬНЫЕ ВОЛНЫ – волны, у которых характеризующие их векторные величины совершают колебания в направлении, параллельном направлению распространения волны. В отличие от поперечных волн продольные волны могут распространяться во всех средах, так как во всех средах при деформации сжатия возникают силы упругости, обеспечивающие распространение этих волн. СКОРОСТЬ ВОЛНЫ- скорость распространения возмущения. Индивидуальное расчётное задание.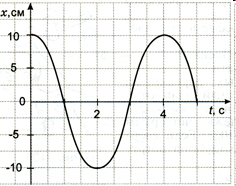



Найти: А- амплитуду; Т- период; ν- частоту; ω- циклическую частоту; Какой длины математический маятник колеблется с этой же частотой? Какой жёсткости должна быть взята пружина для маятника, чтобы та же масса груза колебалась в вертикальной плоскости с частотой в 10 раз большей?

Задача №1. Период колебаний источника волны равен 8 с, скорость распространения волны 13 м/с. Чему равна длина волны?

Задача №2. Определите длину волны, распространяющейся со скоростью 320 м/с, если частота колебаний равна 256 Гц.

Домашнее задание. Выучить конспект. Прочитать § 12.3. Решить задачу: № 438. По поверхности воды в озере волна распространяется со скоростью 6 м/с. каковы период и частота колебаний бакена, если длина волны 3м?