Geum.ru

Учебном процессе программного обеспечения для решения экстремальных задач

Вид материалаДокументы

Содержание


О пакете FinPlus
О пакете GP.
О пакете ORP
Подобный материал:

О создании и использовании в учебном процессе программного обеспечения для решения экстремальных задач

Бухвалова В. В., Рогульская А. С.


Различные типы экстремальных задач рассматриваются во многих математических, экономических курсах и курсах по различным прикладным дисциплинам. При изучении алгоритмов решения этих задач, как обучающим, так и обучаемым желательно иметь специальное (учебное) программное обеспечение (ПО). Это ПО должно удовлетворять ряду требований, среди которых, по мнению авторов, главными являются следующие:

    1. требования, предъявляемые к компьютеру для его установки, должны быть минимальными;
    2. наличие дружественного интерфейса, в частности, использование стандартных постановок задач и обозначений;
    3. поддержка стандартных способов ввода данных задачи и сохранения решения;
    4. возможность не только решения задачи (получения оптимального решения, если оно существует), но и просмотра процесса решения по итерациям;
    5. возможность исследования полученного решения на устойчивость (определения интервалов изменения параметров задачи, при которых оптимальное решение либо остается неизменным, либо легко вычисляется);
    6. возможность проведения тестирования алгоритмов, в частности, по времени решения задачи и количеству выполненных итераций;
    7. возможность генерации случайной экстремальной задачи заданной размерности.


Авторам известен только один пример учебного ПО, которое удовлетворяет первым пяти требованиям из перечисленных выше – это программа TORA. Студенческая версия этой программы распространяется вместе с, видимо, самым популярным в мире учебником по исследованию операций Х. Тахи ([4]). Однако возможность проводить тестирование алгоритмов (п. 6) также является важным элементом обучения. Имея результаты тестирования, можно, например, сравнивать алгоритмы и оценивать увеличение времени решения задач с ростом их размерности. Что касается генераторов задач (п.  7), то они предназначены, прежде всего, преподавателям. Их использование существенно упрощает процесс составления большого числа индивидуальных заданий и их проверку.

Работы по созданию ПО, удовлетворяющего всем перечисленным выше требованиям, проводятся в течение ряда лет на кафедре исследования операций СПбГУ под руководством В. В. Бухваловой. Так как при создании ПО, ориентированного на решение слишком широкого класса оптимизационных задач, как это сделано, например, в надстройке Excel «Поиск решения», трудно выполнить требования, перечисленные выше, было принято решение создать несколько программ (пакетов). Каждый из пакетов предназначен для решения определенного класса экстремальных задач. К настоящему моменту создано три пакета для решения оптимальных задач следующих классов:
  • линейное и квадратичное программирование – пакет FinPlus;
  • геометрическое программирование – пакет GP;
  • дискретные задачи исследования операций – пакет ORP.


В качестве платформы, на базе которой создается ПО, была выбрана программа Microsoft Excel со встроенным в нее языком программирования Visual Basic for Applications (VBA, [6]). Этот выбор был обусловлен тем, что программа Microsoft Office установлена на большинстве компьютеров, работающих под управлением операционной системы Windows. Таким образом, наличие программы Microsoft Excel и является основным системным требованием. Установка на компьютере любого из созданных пакетов предельно проста – достаточно открыть главный xls-файл пакета в режиме, когда допускается использование макросов. Для размещения пакетов (полного набора файлов) на компьютере требуется совсем немного памяти: 1. 90 Мб для пакета FinPlus, 1.07 Мб для пакета GP и 670 Кб для пакета ORP.

Еще раз подчеркнем, что создано ПО, предназначенное, прежде всего, для использования в учебном процессе. Это означает, во-первых, что для реализации были выбраны алгоритмы, которые изучаются в стандартных курсах. Например, задача линейного программирования в пакете FinPlus решается стандартным модифицированным двухфазным симплекс-методом. Но с учетом того, что в курсах по математическому программированию симплекс-метод часто излагается с помощью симплекс-таблиц, предусмотрена возможность просмотра этих таблиц по итерациям. Во-вторых, не ставилась цель решать реальные задачи большого размера также быстро, как это делается коммерческим ПО. Хотя заметим, что, например, решение ряда задач линейного программирования в пакете FinPlus с 30 переменными занимало несколько секунд.

Все пакеты имеют одинаковый дизайн. В качестве примера на рис. 1 приведено главное меню пакета FinPlus. Выбор языка программирования VBA позволяет в полной мере использовать принцип модульности, который упрощает модификацию ПО и использование ранее разработанных модулей при создании нового ПО.


О пакете FinPlus ([1]). Стандартные курсы, посвященные экстремальным задачам, одними из первых рассматривают задачи линейного программирования (ЛП), а как метод их решения – симплекс-метод. Задачи квадратичного программирования (КП) можно решать, используя модификации того же симплекс-метода. Именно поэтому ПО для этих двух классов задач было объединено в один пакет. Для решения задачи КП в пакете реализован метод дополнительного базиса ([3]), который изучают студенты кафедры исследования операций СПбГУ. Версия пакета FinPlus для свободного копирования размещена на сайте exponenta.ru:

enta.ru/educat/systemat/buhvalova/index2.asp.




Рис. 1. Пакет FinPlus: главное меню

Перечислим основные возможности пакета FinPlus:
      1. решение задачи ЛП общего вида;
      2. решение задачи КП общего вида;
      3. формирование листа с отчетом о решении задачи;
      4. ознакомление с работой пакета на примере демонстрационной задачи;
      5. поддержка стандартных способов ввода-вывода и сохранения решения задачи;
      6. редактирование данных задачи на рабочем листе MS Excel;
      7. формирование отчета по итерациям;
      8. для задач ЛП:
  • формирование отчета «Постоптимальный анализ»;
  • тестирование модуля;
  • генерация задачи с заданными параметрами.

На рис. 2 показано, как выглядит лист с данными задачи ЛП:



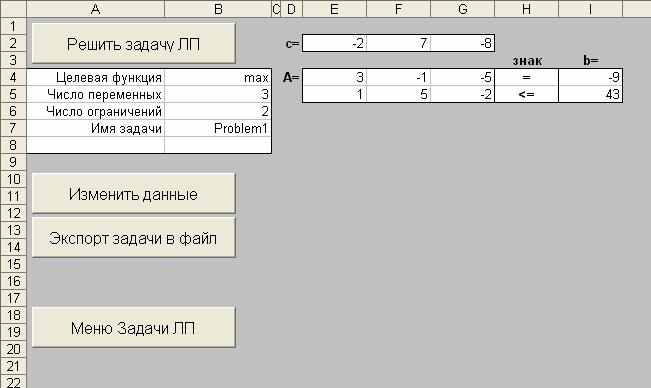
Рис. 2. Пакет FinPlus: рабочий лист с данными задачи ЛП

Отчет «Постоптимальный анализ» отражает результаты исследования решения задачи на устойчивость (рис. 3):




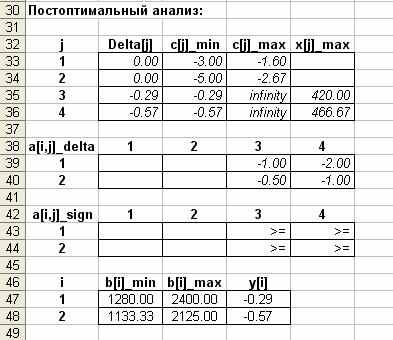
Рис. 3. Пакет FinPlus: отчет «Постоптимальный анализ»


Существует расширенная версия пакета FinPlus, позволяющая дополнительно решать задачи целочисленного ЛП (алгоритм Балаша) и некоторые задачи финансового планирования и портфельного анализа.


О пакете GP. Задачи геометрического программирования (ГП) гораздо реже изучаются в курсах экстремальных задач, чем задачи ЛП и КП. Однако в последние годы ситуация существенно изменилась. Это связано с тем, что были разработаны, во-первых, эффективные методы решения этих задач ([7], [10], [11], [12]), а, во-вторых, методы сведения довольно широкого класса оптимизационных нелинейных задач к задачам ГП ([2], [9]). Для популяризации идей и методов ГП авторы статьи разработали вводный интернет-курс по геометрическому программированию, который, в частности, предполагает использование пакета GP.

Для решения задач ГП в пакете GP реализован двойственный метод, предложенный в [12], который на данный момент считается одним из самых эффективных. Перечислим возможности пакета GP:
  1. решение задачи ГП с ограничениями;
  2. поддержка русского и английского языков;
  3. поддержка стандартных способов ввода-вывода, сохранения данных и решения задачи (рис.4);
  4. формирование отчета по итерациям;
  5. формирование листа с отчетом о решении задачи;
  6. получение информации о времени решения задачи и количестве итераций.




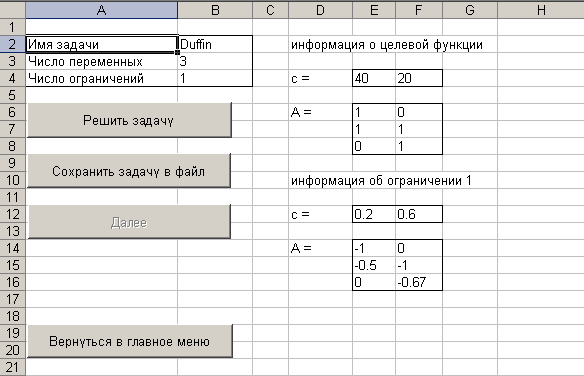
Рис. 4. Пакет GP: рабочий лист с данными задачи ГП

Создание генератора нетривиальных задач ГП является сложной задачей, для решения которой пока не существует подходящего алгоритма. Поэтому в качестве его замены авторами был создан банк задач ГП, состоящий на данный момент из 74 объектов. Банк задач представляет из себя текстовый файл в csv-формате. В нем для каждой задачи указывается: источник, из которого она взята, данные задачи, оптимальное решение и значение целевой функции. Нам представляется, что банк задач ГП будет полезен не только преподавателям при составлении контрольных заданий, но и разработчикам нового ПО для решения нелинейных задач оптимизации в процессе его тестирования.






Рис. 5. Пакет GP: фрагмент банка задач ГП

О пакете ORP ([5]). Текущая версия пакета предназначена для решения следующих дискретных экстремальных задач: о назначениях, коммивояжера, кратчайший путь в графе, минимальное остовное дерево в графе. К настоящему моменту полностью сформирован модуль, связанный с задачей о назначениях (ЗН). Для решения ЗН можно использовать три алгоритма: аукционный ([8]), Мака, эвристический жадный.

Для решения сетевых задач в текущей версии пакета реализованы следующие алгоритмы: задача о кратчайшем пути – алгоритм Дейкстры, задача о минимальном остовном дереве – алгоритм Краскала, задача о коммивояжере – метод ветвей и границ и жадный (эвристический) алгоритм. Перечислим реализованные возможности пакета ORP:

    1. решение задачи о назначении;
    2. решение задачи о коммивояжере;
    3. решение задачи о минимальном остовном дереве в графе;
    4. решение задачи о кратчайшем пути в графе;
    5. поддержка стандартных способов ввода-вывода и сохранения решения задачи;
    6. формирование листа с отчетом о решении задачи;
    7. формирование отчета по итерациям;
    8. тестирование модуля;
    9. формирование файла статистики;
    10. генератор задач.


Файл статистики содержит дату и время начала решения задачи, имя задачи, название алгоритма, с помощью которого данная задача была решена в пакете, размерность матрицы данных, количество итераций, время решения задачи, значение целевой функции и отклонение от оптимального значения (для жадного алгоритма).

На рис. 6 приведен лист с отчетом о решении задачи о назначениях эвристическим алгоритмом:




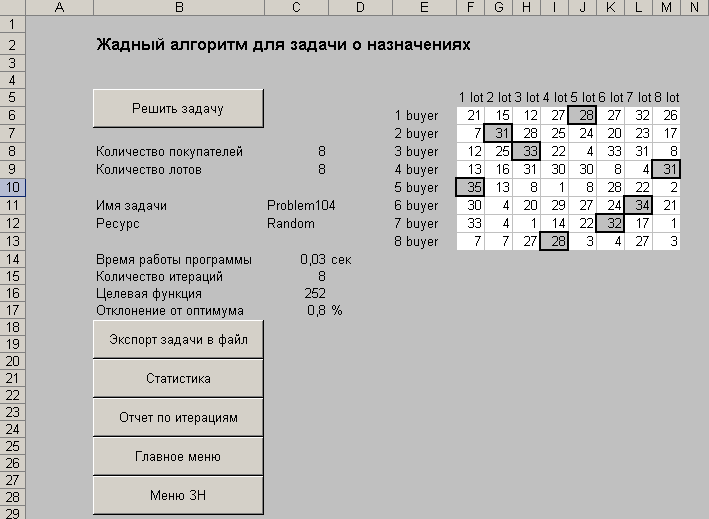
Рис. 6. Пакет ORP: лист c отчетом о решении задачи о назначениях

Литература
  1. Бухвалова В. В. Использование пакета прикладных программ FinPlus в учебном процессе / В. В. Бухвалова, А. В. Ковальчук // Обозрение прикладной и промышленной математики. – 2007. – Том 14, № 1. – с. 95-98.
  2. Бухвалова В. В. Расширение области применимости методов геометрического программирования / В. В. Бухвалова, А. С. Рогульская // Обозрение прикладной и промышленной математики. – 2008. – Том 15, № 2. – с. 270-273.
  3. Даугавет В. А. Численные методы квадратичного программирования / В. А. Даугавет. – СПб.: Изд-во С.-Петерб. ун-та, 2004. – 128 с.
  4. Таха Х. А. Введение в исследование операций / Х. А. Таха; пер. с англ., ред. А. А. Минько. – 7-изд. – М.: Издательский дом «Вильямс», 2005. – 912 с.
  5. Филькина Т. Н. Алгоритмы решения задачи о назначениях: дипломная работа (СПбГУ, кафедра исследования операций). – СПб., 2008.
  6. Уокенбах Д. Microsoft Office Excel 2007: профессиональное программирование на VBA / Д. Уокенбах; пер. с англ. – М.: Издательский дом «Вильямс», 2008. – 928 с.: ил. – (Прикладное программное обеспечение).
  7. Alejandre J. L. A General Alternative Procedure for Solving Negative Degree of Difficulty Problems in Geometric Programming / J. L. Alejandre, A. Allueva, J. M. Gonzalez // Computational Optimization and Applications. – 2004. – No. 27. – p. 83-93.
  8. Bertsekas D.P. A new algorithm for the assignment problem / D. P. Bertsekas // Math. Programming. – 1981. – Vol.1, No.21. - p. 152-171.
  9. Boyd S. A Tutorial on Geometric Programming / S. Boyd, S., J. Kim, L. Vandenberghe, A. Hassibi // Optimization and Engineering. – 2007. – Vol. 8, No. 1. – p. 67-127.
  10. Kortanek K. O. An infeasible interior-point algorithm for solving primal and dual geometric programs / K. O. Kortanek, X. Xu, Y. Ye // Mathematical Programming. – 1997. – No. 76. – p. 155-181.
  11. Liu S. T. Posynomial geometric programming with interval exponents and coefficients / S. T. Liu // European Journal of Operational Research. – 2008. – No. 186. - p. 17-27.
  12. Rajgopal J. Solving Posynomial Geometric Programming Problems via Generalized Linear Programming / J. Rajgopal, D. L. Bricker // Computational Optimization and Applications. – 2002. –No. 21. – p. 95-109.