А. В. Кузовкин московский инженерно-физический институт (государственный университет) математическое описание процесса разработки компонентного программного обеспечения вдоклад
| Вид материала | Доклад |
- И. Ф. Бабалова московский инженерно-физический институт (государственный университет), 39.62kb.
- Д. С. Варганов научный руководитель Н. П. Васильев, к т. н., доцент Московский инженерно-физический, 31.85kb.
- В. А. Карандасов научный руководитель В. П. Румянцев, к т. н., доцент Московский инженерно-физический, 28.6kb.
- А. В. Кузовкин московский инженерно-физический институт (государственный университет), 31.8kb.
- Ю. В. Смирнов московский инженерно-физический институт (государственный университет), 13.81kb.
- Д. В. Гуцко Московский инженерно-физический институт (государственный университет), 34.47kb.
- К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
- В. В. Пивоваров московский инженерно-физический институт (государственный университет), 27.99kb.
- А. В. Кузовкин московский инженерно-физический институт (государственный университет), 27.29kb.
- Е. В. Чепин московский инженерно-физический институт (государственный университет), 30.11kb.
УДК 004.4(06) Технологии разработки программных систем
А.В. АНИСИМОВ, А.В. КУЗОВКИН
Московский инженерно-физический институт (государственный университет)
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА РАЗРАБОТКИ КОМПОНЕНТНОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
В докладе рассматривается один из подходов к математическому описанию крупного программного продукта, имеющего компонентную структуру. В качестве объекта рассмотрения взята большая информационная система, обладающая сложной версионно-временной структурой. Такой подход является одним из необходимых шагов на пути к частичной автоматизации процесса разработки систем данного класса.
Крупная информационная система со сложной версионно-временной структурой является не типичным объектом рассмотрения с точки зрения разработки программного обеспечения. Однако доля таких систем в сфере информационных технологий весьма велика и продолжает стремительно расти.
Специфика таких систем заключается в том, что с некоторой периодичностью (скажем, ежегодно) выпускаются базовые конфигурации системы, которые затем дорабатываются под нужды региона, в котором они будут использоваться, доработанные конфигурации впоследствии изменяются, чтобы соответствовать требованиям каждого заказчика, и так далее. В итоге образуется древовидная версионно-временная структура, в "корнях" которой лежат базовые конфигурации, а ветви образованы производными конфигурациями системы, появляющимися в разные периоды времени. На рис. 1 схематично представлено дерево конфигураций такой системы.
При разработке (доработке) такой системы возникает большое число вопросов, которые приходится решать вручную, в то время как некоторая часть задач может быть автоматизирована. Примером такой задачи может являться задача переноса функциональности между разными конфигурациями системы. Процесс переноса функциональности для общего случая автоматизировать невозможно, но весьма большая доля проделываемой программистом работы может быть выполнена машиной.
Таких задач можно найти достаточно много. Но для их автоматизации необходимо иметь некоторый точный аппарат, с помощью которого систему удалось бы описать математически и иметь возможность оперировать математическими величинами. В данной статье приводится один из возможных вариантов такого математического описания (представления) системы. В качестве математического аппарата были выбраны множества [1]. Система, а, вернее, процесс её разработки и построения, описывается с помощью теоретико-множественной модели [2].
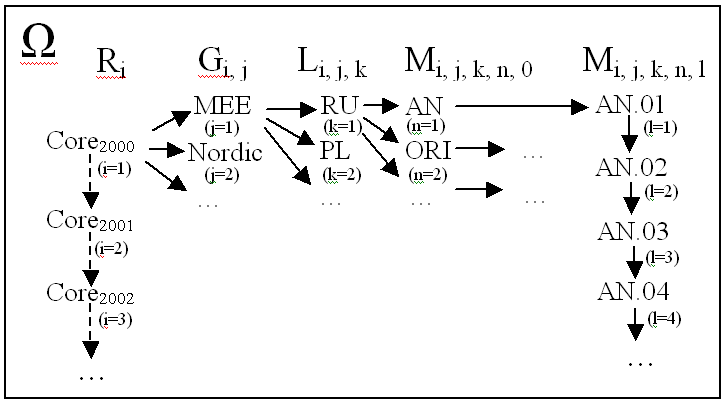
Рис. 1. Дерево конфигураций системы.
Подход заключается в разделении системы на классы конфигураций и представление конфигурации как подмножества некоторого множества
 . Множество
. Множество  является множеством всех исходных кодов системы таких, что
является множеством всех исходных кодов системы таких, что  – множество упорядоченных двоек
– множество упорядоченных двоек  ,
,  ,
,  , где
, где  – множество названий исходных кодов,
– множество названий исходных кодов,  – множество индексов исходных кодов.
– множество индексов исходных кодов.Такой подход позволяет строить модели, описывающие различные аспекты функционирования систем, что является основой для разработки алгоритмов автоматизации ряда процессов [3]. Автор данной статьи в настоящее время использует данный подход для реализации алгоритма переноса функциональности между различными конфигурациями системы.
Список литературы
- Кантор Г. Труды по теории множеств. М: Наука 1965.
- Бусленко Н.Б. Моделирование сложных систем. М: Наука 1968. 342 с.
- Овчинников В.А. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем. М: МГТУ 2001. 94-141 с.
ISBN 5-7262-0710-6. НАУЧНАЯ СЕССИЯ МИФИ-2007. Том 2
