Geum.ru

Название файла

Вид материалаДоклад
Подобный материал:

Внимание!!! Название файла тезисов должно соответствовать имени докладчика латиницей

Cx-X

Моделирование фрактальной структуры агрегатов дисперсных частиц сферической формы

Н. Ф. Бункин, А. В. Старосветский, А. В. Шкирин, В. А. Козлов

Институт Общей Физики им. А.М. Прохорова РАН, Москва, Россия

Агрегация частиц дисперсной фазы с образованием кластеров разнообразной пространственной структуры существенно влияет на физические свойства дисперсных систем, таких как, например, коллоиды и нанокомпозитные материалы. Поэтому изучение процессов кластеризации дисперсных частиц является актуальной проблемой. В качестве эффективного средства бесконтактной диагностики дисперсных систем широко применяется метод измерения угловых зависимостей элементов матрицы рассеяния лазерного излучения, которые оказываются чувствительными к форме и распределению рассеивающих частиц по размерам. В рамках этого метода нами предлагается математический подход к восстановлению кластерной структуры дисперсной фазы путем аппроксимации угловых зависимостей матрицы рассеяния теоретическими кривыми, вычисленными как среднее по ансамблю стохастических кластеров сферических частиц. С этой целью была разработана математическая модель иерархического роста фрактальных кластеров сферических частиц, учитывающая кластер–кластерную агрегацию. В данной модели кластер–кластерной агрегации средняя фрактальная размерность генерируемых ансамблей кластеров сферических частиц имеет монотонную зависимость от параметра модели , задающего зависимость вероятности участия кластера в акте коагуляции от объема кластера. Введение этого параметра предоставляет новую «степень свободы», которая дает возможность влиять на форму кривой и равномерно приближать соответствующую теоретическую индикатрису рассеяния к экспериментальным точкам. Созданный на основе этой модели программный модуль для компьютерной генерации случайных реализаций кластеров сферических частиц и программа численного расчета рассеяния электромагнитных волн отдельным кластером, были объединены в программный комплекс, позволяющий вычислять статистические характеристики рассеяния оптического излучения системами с заданным числом кластеров, их распределением по размерам и типом агрегации.

Конкретная задача, поставленная в данной работе, была связана с исследованием указанным методом законов формирования естественной гетерогенности в системах жидкость – растворенный газ. С помощью программного комплекса были проведены численные эксперименты по моделированию матрицы рассеяния света на кластерах нанопузырьков в водных растворах электролитов, позволившие более точно оценить среднюю фрактальную размерность таких кластеров и параметры распределения по размерам нанопузырьков в их составе. Анализ результатов компьютерных экспериментов позволил сформулировать общие закономерности углового поведения матрицы рассеяния света для больших выборок кластеров, полученных в соответствии с различными механизмами агрегации. Методом минимизации функционала отклонения расчетных функций от данных физического эксперимента на равномерной сетке значений параметров ансамблей кластеров иерархического типа были определены численные значения статистических характеристик нанопузырьковых кластеров в водном 0.8 М растворе NaCl: 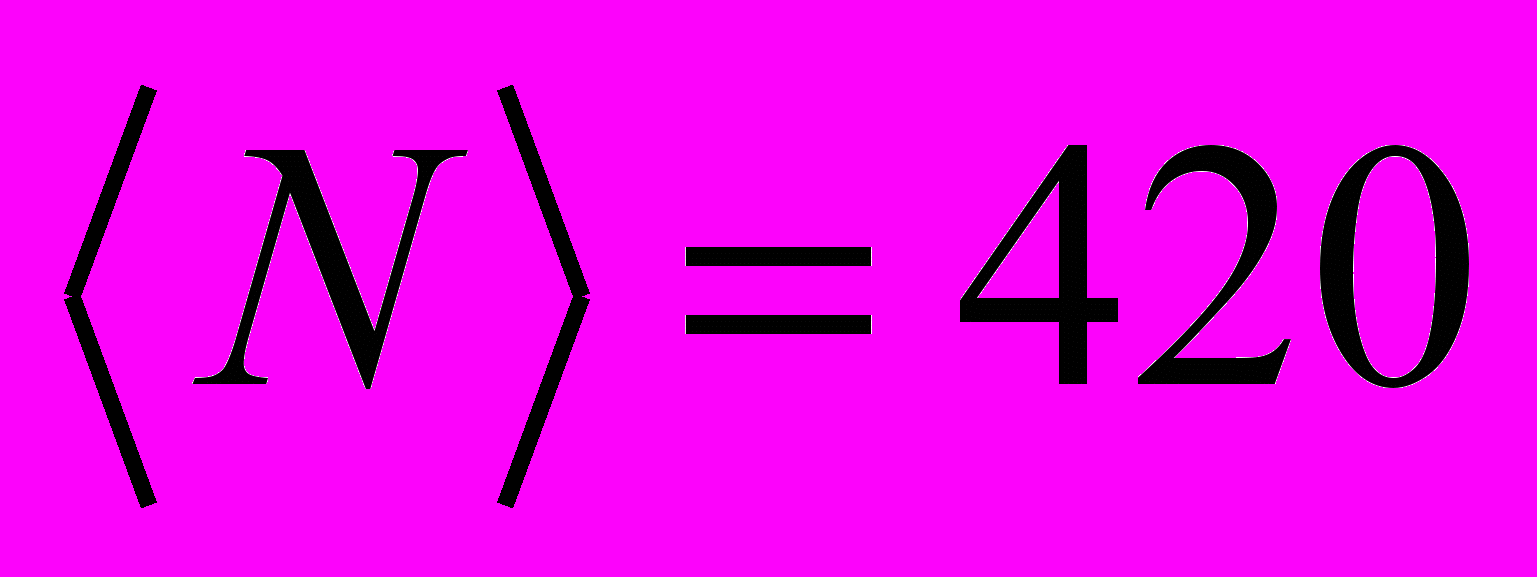– среднее количество частиц-мономеров в кластере, 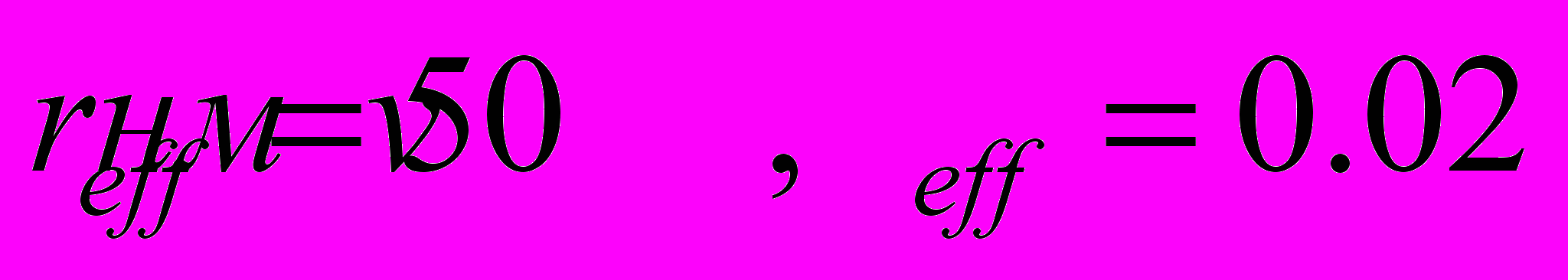– эффективный радиус и эффективная относительная ширина логнормального распределения по размерам мономеров, 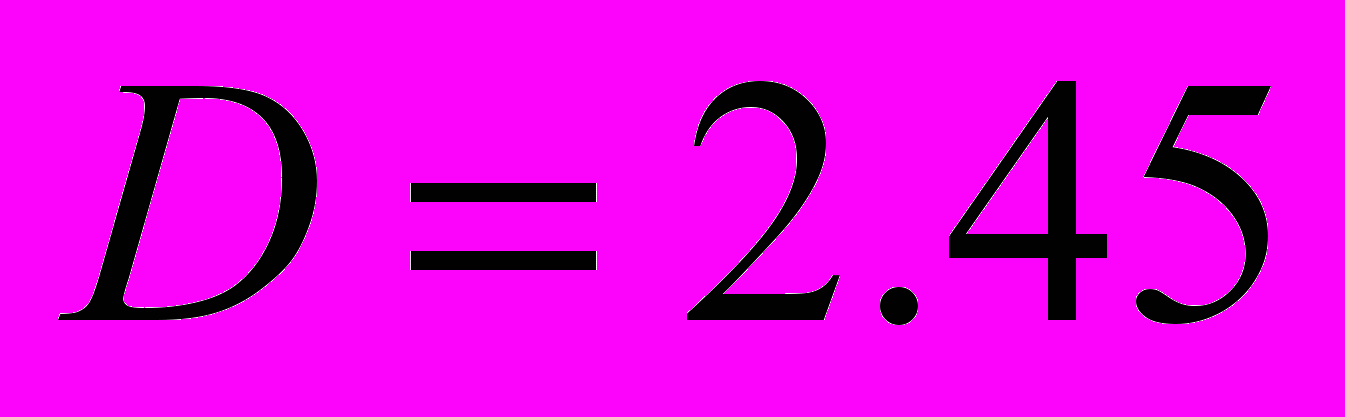– средняя фрактальная размерность по выборке из 200 кластеров.


1. N. F. Bunkin, S. O. Yurchenko, N. V. Suyazov, A. V. Starosvetskiy, A. V. Shkirin, V. A. Kozlov, Modeling the cluster structure of dissolved air nanobubbles in liquid media // (Mathematics Research Developments, Classification and Application of Fractals, Nova Science Publishers: 2011).

2. Н. Ф. Бункин, Н. В. Суязов, А. В. Шкирин, П. С. Игнатьев, К. В. Индукаев, ЖЭТФ, 135, № 5: 917-937 (2009).