Вестник тгасу №1, 2005

Вид материала

Документы

Содержание Математическая модель пластической деформации скольжения Структура пакета прикладных программ Численный метод Представление результатов расчетов Библиографический список

Подобный материал:

• Вестник тгасу №2, 2000, 205.29kb.
• Методические указания к курсовой работе для студентов и слушателей ино-тгасу составители, 1167.21kb.
• Вестник банка россии, 2020.43kb.
• Вестник банка россии, 1295.25kb.
• М. А. «Proteia antropolatria». Диагноз болезни от Константина Леонтьева, 369.71kb.
• В. Б. Безгин Кафедра истории и философии тгту, 188.78kb.
• Научная литература «Вестник Московского государственного университета леса – Лесной, 1372.53kb.
• Развитие России во второй половине 19 века, 38.64kb.
• Аннотация, 232.88kb.
• Вендров А. М. Case-технологии. Современные методы и средства проектирования информационных, 9.59kb.

Колупаева С.Н., Семенов М.Е. Пакет прикладных программ для исследования пластической деформации скольжения в г.ц.к. материалах // Вестник ТГАСУ. – 2005. – №1. – С. 36-46.


УДК 539.2+004.422.8

С.Н. Колупаева, канд. физ.-мат. наук, доцент, ТГАСУ, г. Томск

М.Е. Семенов

ПАКЕТ ПРИКЛАДНЫХ ПРОГРАММ для ИССЛЕДОВАНИЯ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ скольжения В Г.Ц.К. МАТЕРИАЛАХ

Разработан пакет прикладных программ SPFCC для описания закономерностей пластической деформации скольжения в г.ц.к. материалах. Для расчетов используется математическая модель, базирующаяся на системе дифференциальных уравнений баланса деформационных дефектов в г.ц.к. материалах. Поскольку процессы генерации и аннигиляции дефектов являются существенно разноскоростными, система дифференциальных уравнений является жесткой. Для решения жесткой системы ОДУ в пакете использован неявный метод Гира переменного порядка. Пакет программ SPFCC ориентирован на пользователей, имеющих различную квалификацию в области программирования и работы с системами ОДУ.

Введение

Пластическое поведение и свойства кристаллических материалов существенно определяются совместным, как правило, нелинейным взаимообусловленным влиянием текущего дефектного состояния, типа и параметров деформирующего воздействия, характеристик материала и упрочняющих фаз. Для исследования закономерностей пластической деформации в широком спектре характеристик материалов и параметров приложенного воздействия одним из наиболее перспективных подходов является последовательное создание, развитие и применение математических моделей механизмов и процессов, определяющих основные явления пластичности. В широком спектре условий доминирующим явлением, обеспечивающим макроскопическое формоизменение материалов, является кристаллографическое скольжение. При исследовании процессов пластической деформации в кристаллических материалах широко используются математические модели, основанные на уравнениях баланса деформационных дефектов [1–8]. И соответственно исследователю часто приходится работать с системами ОДУ (обыкновенных дифференциальных уравнений), которые часто являются жесткими, а их решение – весьма нетривиальной задачей.

Современная вычислительная техника позволяет решать задачи автоматизации расчетов при решении сложных математических задач. В настоящее время существует множество специализированных математических пакетов программ (Maple, Mathematica, MathCad, MATLAB и другие), позволяющих решать системы дифференциальных уравнений. В пакеты программ заложены, как правило, классические методы из семейства методов Рунге-Кутты, а также специализированные методы для решения жестких систем ОДУ. Заметим, что при решении задач с использованием математических пакетов пользователь должен иметь достаточное представление о методах решения ОДУ, а также навыки работы с пакетом программ и, как правило, программирования на внутреннем языке пакета.

В работе ставится задача создания специализированного пакета прикладных программ с развитым интерфейсом пользователя для описания закономерностей пластической деформации скольжением в г.ц.к. материалах.


Математическая модель пластической деформации скольжения

в г.ц.к. материалах


Процессы пластической деформации скольжения определяются, главным образом, образованием, движением, взаимодействием и аннигиляцией дефектов, прежде всего дислокаций и точечных дефектов, поэтому весьма эффективно при описании закономерностей пластической деформации скольжения использование математических моделей, основу которых составляют уравнения баланса деформационных дефектов [1–11].

При пластической деформации скольжения образуются, преимущественно, дислокации различного типа и точечные дефекты, определяющими механизмами их генерации являются процессы производства дефектов при формировании зон кристаллографического сдвига [5-8]. Деформация скольжения непосредственно связана с изменением плотности дислокаций, поскольку расширение дислокационных петель приводит к увеличению как деформации сдвига, так и плотности дислокаций. Кроме того, при скольжении дислокации производят различные атомные деформационные дефекты, образуют дислокационные дипольные и мультипольные конфигурации, а в дисперсно-упрочненных материалах еще и геометрически необходимые дислокации у частиц второй фазы, то есть скольжение порождает дефектную среду. Эта среда, в свою очередь, взаимодействует с дислокациями, образующими зоны сдвига, оказывая на них существенное и разнообразное влияние. Процессы аннигиляции носят преимущественно диффузионный характер, реализуются в дефектной среде в целом, создаваемой совокупностью дефектов, порожденных скольжением в большом числе зон сдвига.

Для моделирования процессов пластической деформации в г.ц.к. материалах при разработке пакета прикладных программ используется математическая модель, базирующаяся на системе обыкновенных дифференциальных уравнений баланса деформационных дефектов, сформулированная в работах [9–12]. Математическая модель включает уравнения баланса сдвигообразующих дислокаций, дислокаций в дипольных конфигурациях межузельного и вакансионного типа, межузельных атомов, моно- и бивакансий, в дисперсно-упрочненных материалах дополнительно дислокационных призматических петель межузельного и вакансионного типа; уравнение, связывающее скорость деформации с напряжением и плотностью дислокаций; уравнение, описывающее приложенное воздействие [11, 12].

В общем виде систему ОДУ баланса деформационных дефектов можно представить следующим образом:

, (1)

где , – функции генерации, аннигиляции и релаксационной трансформации деформационных дефектов соответственно, – вектор переменных, характеризующих дефектную среду, – вектор переменных, характеризующих внешнее воздействие, t – независимая переменная. Для нахождения решения задачи Коши начальные условия зададим в виде: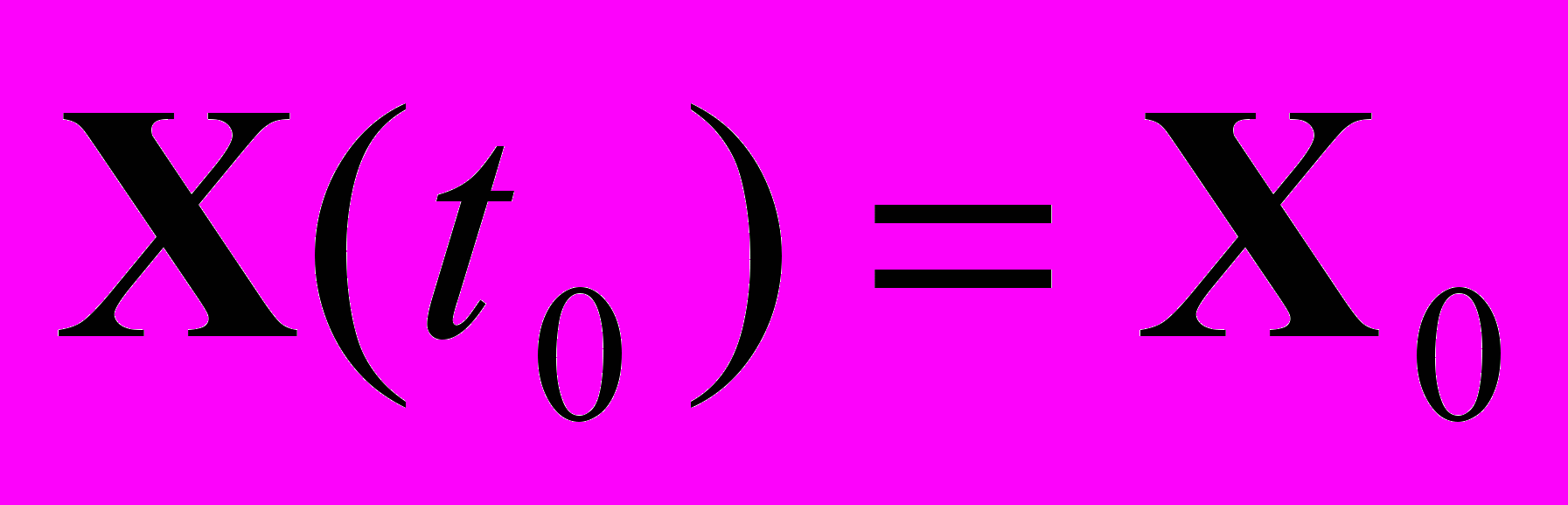

. (2)

Различными авторами рассмотрен ряд механизмов аннигиляции дислокаций и показано, что основными механизмами аннигиляции дислокаций являются переползание невинтовых дислокаций в результате осаждения на их экстраплоскостях точечных дефектов и аннигиляция винтовых дислокаций при их поперечном скольжении [1-11]. В пакете программ SPFCC в частных моделях аннигиляции деформационных точечных дефектов рассмотрены следующие стоки: 1) для межузельных атомов – невинтовые дислокации, моновакансии, бивакансии; 2) для моновакансий – невинтовые дислокации, межузельные атомы, моновакансии; 3) для бивакансий – невинтовые дислокации, межузельные атомы. Образующиеся при встрече двух бивакансий или моновакансии и бивакансии комплексы точечных дефектов в настоящей работе не рассматриваются. Для аннигиляции дипольных дислокационных конфигураций рассмотрены следующие механизмы: 1) уменьшение плеча дислокационных диполей вакансионного типа до их аннигиляции при осаждении на них межузельных атомов и дислокационных диполей межузельного типа при осаждении на них моновакансий и бивакансий; 2) увеличение плеча дислокационных диполей вплоть до потери их устойчивости. Аналогичные механизмы аннигиляции рассмотрены для дислокационных призматических петель при осаждении на них точечных дефектов. Уравнения баланса деформационных дефектов записаны в предположении, что все пороги, находящиеся на околовинтовых составляющих дислокационной петли, движутся вместе с дислокацией и производят точечные дефекты [9-12].

Частные модели механизмов генерации и аннигиляции деформационных дефектов создают основу для формирования моделей пластической деформации скольжения с различным набором уравнений баланса деформационных дефектов и учитываемых механизмов генерации и аннигиляции деформационных дефектов и дают возможность исследования роли различных механизмов и процессов в закономерностях пластического поведения и эволюции деформационной дефектной среды в монокристаллах г.ц.к. металлов и дисперсно-упрочненных сплавов на их основе при различных условиях деформирования и приложенных воздействиях.


Структура пакета прикладных программ

Для реализации математической модели пластической деформации скольжения [9-12] создан пакет прикладных программ Slip Plasticity of Face-Centered Cubic v1.0 (SPFCC). Разработка программного продукта производится в рамках развития модели пластической деформации в кристаллических материалах [9–12]. В связи с этим перед разработчиками стояли следующие задачи: 1) обеспечить максимальную гибкость программного кода и логической структуры пакета в целом для простоты сопровождения, модификации и расширения пакета прикладных программ, 2) сделать представление входных-выходных данных удобным для пользователя.

Пакет SPFCC разработан с использованием языка программирования Object Pascal под управлением операционной системы Microsoft Windows [13, 14]. Целевая аудитория: студенты, аспиранты, специалисты, занимающиеся исследованиями в области пластичности и прочности. Для работы с пакетом необходимо знакомство с основами работы приложений под управлением MS Windows. Данная версия пакета программ позволяет проводить расчеты для случая деформирования кристалла с медной, алюминиевой или никелевой матрицей при постоянной скорости деформации, при постоянном приложенном напряжении, при постоянной нагрузке (для растяжения и сжатия). Пакет позволяет проводить серии расчетов в автоматическом режиме при выбранном варьируемом параметре модели (например, температуре, скорости деформирования) и заданных нижнем и верхнем пределах его изменения.

Для различных материалов (однофазный, дисперсно-упрочненный) и деформирующих воздействий число уравнений в системе (1) различно, кроме того сами уравнения могут быть кусочно-сшитыми. Этот факт учтен при программировании, и пользователь имеет возможность сформировать явный вид системы (1) в диалоговом режиме или выбрать по умолчанию (в этом случае учитывается максимальный возможный набор дефектов и механизмов). При написании пакета программ использован объектно-ориентированный подход, который обеспечивает разработчику гибкую возможность дальнейшей модификации, расширения пакета новыми программными модулями, предназначенными для описания различных типов материалов и воздействий (в настоящее время для этих целей в пакет заложено 8 модулей) или альтернативными численными методами решения задач.

Согласно поставленным задачам приложение функционально разделено на взаимодействующие, но максимально независимые части. Настоящая версия пакета SPFCC состоит из следующих блоков:

• исходные данные,
  
• расчетный блок,
  
• база данных и
  
• справка,
  

взаимосвязанных между собой через Головной модуль, который осуществляет общее управление работой пакета программ и взаимодействие с пользователем. Принципиальная схема взаимодействия блоков пакета представлена на рис. 1.





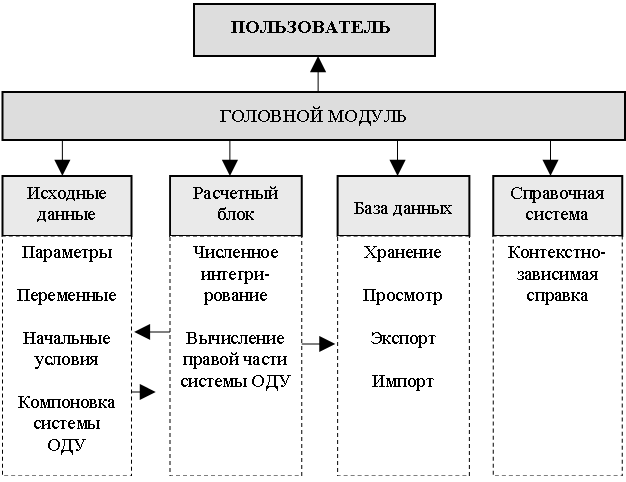
Рис. 1. Принципиальная схема взаимодействия блоков пакета.


Работа пакета SPFCC начинается с загрузки ресурсов приложения, создания сеанса связи с источником данных (блок база данных), загрузки конфигурации и создания главного окна приложения (рис. 2). Выполнение этих операций возложено на головной модуль. В верхней части главного окна расположены меню, с его помощью обеспечивается доступ пользователя к функциям приложения. Заканчивая работу, приложение сохраняет текущую конфигурацию, выгружает из оперативной памяти ресурсы программы, разрывает соединение с источником данных. В левой части рабочей области главного окна (рис. 2) находится иерархическая группа переключателей «Дефекты», реализованная в виде дерева. Пользователь в рамках предложенной модели может определить набор механизмов генерации и аннигиляции деформационных дефектов (в правой части системы ОДУ), которые будут использованы в расчетах, или воспользоваться выбором по умолчанию. По умолчанию в систему ОДУ включаются все механизмы. В правой части рабочей области главного окна (рис. 2) находится список результатов расчетов.





Рис. 2. Общий вид главного окна пакета SPFCC


Блок исходные данные предназначен для инициализации значений параметров пакета. Модули, входящие в состав блока исходные данные, считывают и обрабатывают требуемые для данного случая значения входных параметров модели, формируют необходимые списки и массивы, устанавливаются их размерность.

Интерактивное взаимодействие система-пользователь, реализованное с помощью графического интерфейса, позволяет пользователю в режиме диалога задать значения параметров материала и деформирующего воздействия, начальные условия задачи Коши, значения параметров численного метода решения или воспользоваться значениями параметров, предложенных по умолчанию. Эти функции осуществляет «Менеджер входных данных», реализованный в отдельном диалоговом окне (рис. 3). В случае задания пользователем неверных значений параметров (например, значение параметра не имеет физического смысла) выдается сообщение с предупреждением. При выборе значений параметров модели отличных от значений по умолчанию в базе данных формируются записи, в которых хранятся значения параметров, указанные пользователем. При необходимости эту информацию можно выгрузить в текстовый файл [13, 14].





Рис. 3. Общий вид окна «Менеджер входных данных»


Порядок действий по определению значений параметров, переменных и начальных условий не имеет значения.

Входными данными пакета прикладных программ являются:

• исходная плотность дислокаций и точечных дефектов;
  
• значения параметров, характеризующих материал: модуль сдвига, энергия образования и миграции точечных дефектов, коэффициент Пуассона, модуль вектора Бюргерса и т.п.;
  
• условия деформирования: способ нагружения, скорость деформирования;
  
• нефизические (вспомогательные) величины: минимальный и максимальный шаги интегрирования, интервал интегрирования, погрешность вычислений.
  

После считывания данных от интерфейса пользователя во внутренние переменные пакета блок исходные данные возвращает управление Головному модулю, который в свою очередь передает его дальше - расчетному блоку, который осуществляет проведение расчетов с автоматическим сохранением результатов в источнике данных (блок база данных).


Численный метод

Расчетный блок пакета SPFCC состоит из 16 основных подпрограмм. Вычислительные методы, используемые в пакете прикладных программ с необходимостью должны быть пригодны для решения систем ОДУ различной жесткости, поскольку возникающие при работе с математической моделью пластической деформации задачи часто являются жесткими. Жесткость не является простым определением, имеющим четкое математическое описание. Решение жесткой системы содержит как «быстро убывающие», так и «медленно убывающие» составляющие [15–17]. Начиная с некоторого значения независимой переменной интегрирования (в нашем случае это время или степень деформации) решение системы ОДУ почти полностью определяется медленно убывающей составляющей.

В расчетном блоке пакета использованы линейный многошаговый неявный метод прогноза-коррекции Адамса и линейный многозначный неявный метод прогноза-коррекции Гира переменного порядка в представлении Нордсика. Метод Адамса используется для построения грубого прогноза решения с последующим итеративным уточнением. Метод Гира - жестко устойчивый метод при любой величине шаге интегрирования, и поэтому шаг интегрирования можно выбирать произвольно, руководствуясь лишь соображениями точности, а не устойчивости [15–17]. Использованный подход Нордсика хранения информации назад позволяет эффективно (в смысле экономии времени счета и оперативной памяти) управлять как порядком численного метода интегрирования, так и шагом интегрирования [15]. С использованием численных методов решения, включенных в пакет программ, можно найти приближенное численное решение в заданных точках с шагом, указанным пользователем.

Для обеспечения надежности и эффективности работы вычислительного метода проведено тестирование вычислительного модуля пакета SPFCC на известных системах уравнений различной жесткости (задача Ван дер Поля, система Робертсона и другие) [17]. Тестирование, проведенное на жестких системах ОДУ, свидетельствует о надежности методов и алгоритма, используемых в пакете SPFCC.


Представление результатов расчетов

В ходе вычислительных экспериментов полученные результаты автоматически сохраняются в локальной реляционной СУБД Microsoft Access (блок база данных). Пользователь не обременен рутинными операциями по работе с файлами, кроме того, благодаря использованию базы данных, у него есть возможность вернуться к ранее сохраненным результатам вычислений и провести сравнение и анализ данных, относящихся к различным наборам значений параметров математической модели пластической деформации скольжения [9-12].

Доступ пользователя к информации хранимой в базе данных осуществляется при помощи интерфейсных форм (обычных Windows-диалогов), сформированных средствами Object Pascal с использованием структурированного языка запросов SQL. Благодаря использованию языка SQL по запросу пользователя можно сформировать таблицу значений переменных системы уравнений на заданном интервале независимой переменной с заданным шагом, построить температурную или скоростную зависимость переменных системы уравнений, вычислить латентную энергию по имеющейся информации о значениях переменных системы уравнений баланса деформационных дефектов.

В пакете прикладных программ реализована возможность предварительного просмотра результатов моделирования в графическом виде (рис. 4). Построенные зависимости можно сохранить в графические виде (формат файла Windows Metafile) или выгрузить результат соответствующего SQL-запроса в текстовый файл и просмотреть результаты с помощью любого текстового редактора  (рис. 5) [13, 14].





Рис. 4. Окно «Графическая интерпретация результатов»





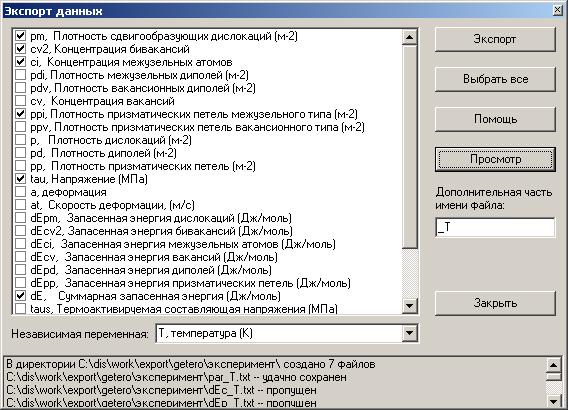
Рис. 5. Окно «Экспорт данных»


С использованием пакета SPFCC проведены расчеты кривых деформационного упрочнения, эволюции дефектной подсистемы и латентной энергии пластической деформации для г.ц.к. металлов в различных условиях, с использованием значений параметров, характерных для наиболее полно представленных теоретическими и экспериментальными исследованиями монокристаллов меди, никеля и алюминия и сплавов на их основе [9-12, 18]. Проведен анализ влияния характеристик материала, деформирующего воздействия и исходного дефектного состояния материала на закономерности деформационного упрочнения и развитие деформационной дефектной подсистемы в г.ц.к. металлах и сплавах на их основе [9-12, 18].

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Акулов Н.С. Дислокации и пластичность. — Минск: Издательство АН БССР, 1961. — 109 с.
   
2. Гилман Дж. Микродинамическая теория пластичности // Микропластичность. — 1972. — С. 18-37.
   
3. Lagneborg R. Dislocation mechanisms in creep // Intern. Metals. Rev. —1972. — P. 130-146.
   
4. Essmann V. Annihilation of dislocations during tensile and cyclic deformation and limits of dislocation densities / V. Essmann, H. Mughrabi // Phil. Mag. (a). — 1979. — № 6. — p. 731-756.
   
5. Попов Л.Е. Концепция упрочнения и динамического возврата в теории пластической деформации / Л.Е. Попов, В.С. Кобытев, Т.А. Ковалевская // Известия вузов. Физика. — 1982. — № 6. - С. 56-82.
   
6. Кобытев В.С. Математическое моделирование сдвиговых процессов пластической деформации. 1. Уравнения кинетики пластической деформации / В.С. Кобытев, С.Н. Колупаева, Л.Е. Попов // Пластическая деформация сплавов. — Томск: Издательство Томского университета, 1986. — С. 23-37.
   
7. Математическое моделирование пластической деформации / Л.Е. Попов, Л.Я. Пудан, С.Н. Колупаева и др. — Томск: Издательство Томского университета, 1990. — 185 с.
   
8. Ковалевская Т.А. Математическое моделирование пластической деформации гетерофазных сплавов / Т.А. Ковалевская, И.В. Виноградова, Л.Е. Попов. — Томск: Издательство Томского университета, 1992. — 167 с.
   
9. Колупаева С.Н. Математическое моделирование деформационного упрочнения дисперсно-упрочненных материалов с не когерентной упрочняющей фазой / С.Н. Колупаева, Е.В. Комарь, Т.А. Ковалевская // Физическая мезомеханика. — 2004. — Т. 7, Спец. выпуск. — № 1. — С. 23-26.
   
10. Попов Л.Е. Математическое моделирование пластической деформации скольжения в дисперсно-упрочненных материалах / Л.Е. Попов, Т.А. Ковалевская, С.Н. Колупаева // Структурно-фазовые состояния и свойства металлических систем. — Томск: Издательство НТЛ, 2004. — С. 135-163.
    
11. Колупаева С.Н. Латентная энергия пластической деформации дисперсно-упрочненных материалов с недеформируемыми частицами. — Том. гос. архит.-строит. ун-т. — Томск, 2004. — 41c. - Деп. в ВИНИТИ 06.08.2004, № 1372-В2004.
    
12. Kolupaeva S.N. Mathematical modeling of temperature and rate dependences of strain hardening in f.c.c. metals / S.N. Kolupaeva, S.I. Puspesheva, M.E. Semenov // Abstract Book. 11th International Conference on Fracture. — Turin(Italy): March 20-25, 2005. — P. 847.
    
13. Semenov M.E. Development of computer programm for the description of plastic deformation by slip / M.E. Semenov, S.N. Kolupaeva // The 7th Korea-Russia International Symposium on Science and Technology (KORUS 2003). — 2003. — June. — P. 401-404.
    
14. Семенов М.Е. Автоматизация расчетов закономерностей пластической деформации в г.ц.к. материалах при деформации / М.Е. Семенов, С.Н. Колупаева // Доклады Томского государственного университета систем управления и радиоэлектроники. Автоматизированные системы обработки информации, управления и проектирования. — Томск, 2003. — Т. 8. — С. 127-133.
    
15. Брайтон Р. Новый эффективный алгоритм для решения дифференциальных систем / Р. Брайтон, Ф. Густавсон // Труды института электро- и радиоинженеров. — 1972. — Т. 60, № 1. — С. 124-132.
    
16. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения): Учеб. пособие для вузов. — М.: Высшая школа, 2001. — 382 с.
    
17. Каханер Д. Численные методы и программное обеспечение / Д. Каханер, К. Моулер, С. Нэш. — М.: Мир, 1998. — 320 с.
    
    
    

Материал поступил в редакцию 31.05.2005.

S.N. Kolupaeva, m.e. semenov

computer programm for the description of plastic deformation by slip IN FCC Materials

The interface and structure of the package of applied programs for the description of plastic deformation by slip in f.c.c.-materials were developed. The mathematical model, which is used for calculations, is based on the set of differential equations of balance of deformation defects in f.c.c.-materials. The system of ODE (ordinary differential equations) is stiff because the processes of generation and annihilation of deformation defects have essentially different rates. Implicit Gear's method of the variable order is used for decision ODE. SPFCC is oriented for the users who have different qualification in programming and experience of decision of ODE systems.