Научный к ф. м н., профессор, Пронин Л. Н. Почти все о кубе вданной работе автор попытался собрать научную информацию, связанную с кубом
| Вид материала | Документы |
- История Сальсы, 28.61kb.
- Почти все о мастеринге, 621.16kb.
- Задачи: Предоставить детям и подросткам объективную научную информацию о психоактивных, 256.15kb.
- Все секретное и тайное всегда вызывает повышенный интерес общественности, 2791.23kb.
- Быт, традиции, культура, 1354.38kb.
- Оценка программы Вданной лекции ( шаг 2 ) представлены литературные источники и базы, 308.47kb.
- Автор: андрей нефедов, 10348.76kb.
- Пронин В. А. Искусство и литература, 504.7kb.
- Программа вступительного экзамена по специальности 10. 01. 01 Русская литература, 2911.66kb.
- Программа кандидатского экзамена по специальности 10. 01. 01 Русская литература, 2045.28kb.
УДК 510
M.Я.Болотин
Группа 3581
Научный руководитель: к. ф.-м. н., профессор, Пронин Л.Н.
ПОЧТИ ВСЕ О КУБЕ
В данной работе автор попытался собрать научную информацию, связанную с кубом. Особое внимание уделено его теоретико-групповым свойствам. В связи с этим в ней излагаются общие сведения из теории групп. В работе предлагается описание группы вращений куба с помощью поворотов вокруг его осей симметрии, а за образующие приняты центральные вращения. Применено представление группы подстановками, определены все подгруппы группы вращений и построена схема структуры подгрупп, в том числе и нормальных делителей. Определены правила перемножения элементов группы с помощью подстановок и определяющих соотношений. Указана связь с теорией Галуа.
Занумеруем начальное положение куба номерами его вершин. Первые четыре номера соответствуют переднему плану и вторые – заднему. Начальному положению куба соответствует тождественная подстановка из восьми элементов. При повороте куба на переднем и заднем плане появляются другие номера, они и определяют новое положение куба. Сопоставим каждому повороту эту подстановку. Таким образом, нашу группу мы рассматриваем как подгруппу подстановок из 8 элементов.
В качестве образующих группы выбраны повороты: α, β, γ на 90 градусов вокруг центральных осей симметрии. С помощью именно этих поворотов мы находим все остальные положения куба. В работе представлен перечень элементов группы и их геометрический смысл. Из геометрического описания следует, что раскрашенный куб можно вернуть в прежнее положение одним поворотом вокруг одной из осей симметрии.
Исследования показали, что в группе G (группа вращений куба), помимо тривиальных, содержится 9 подгрупп 2-го порядка H2i (1≤i≤9), 4 подгруппы 3-го порядка H3i (1≤i≤4), 7 подгрупп 4-го порядка H4i (1≤i≤7). Кроме того, имеются четыре неабелевы группы 6-го порядка H6i (1≤i≤4), о существовании которых не удалось найти сведений в рассмотренных источниках, три неабелевы подгруппы 8-го порядка H8i (1≤i≤3) и одна неабелева подгруппа 12-го порядка H12. Общее количество подгрупп равно 30. В работе перечисляются элементы всех этих подгрупп.
Автор в дальнейшем предполагает описание так называемых «кубиков Рубика», начиная от двухслойного.
УДК 519.852.33
Алексеенко М.А., Шаненко Д.Е.
Группа 1381
Научный руководитель: к.э.н., профессор Петрова Л.Ф.
Решение задачи о назначениях венгерским методом
Задача о назначениях является задачей линейного программирования. Она позволяет решать задачи типа: как наилучшим образом назначить людей на различные должности (что и определило название задачи), чтобы максимизировать прибыль или минимизировать затраты на заработную плату.
К этой группе задач также относятся задачи оптимального исследования рынка и оптимального использования торговых агентов и ряд других.
Математически данная задача может быть записана в следующем виде:
Имеется n работ и n кандидатов для их выполнения. Затраты i-того кандидата на выполнение j-той работы равны
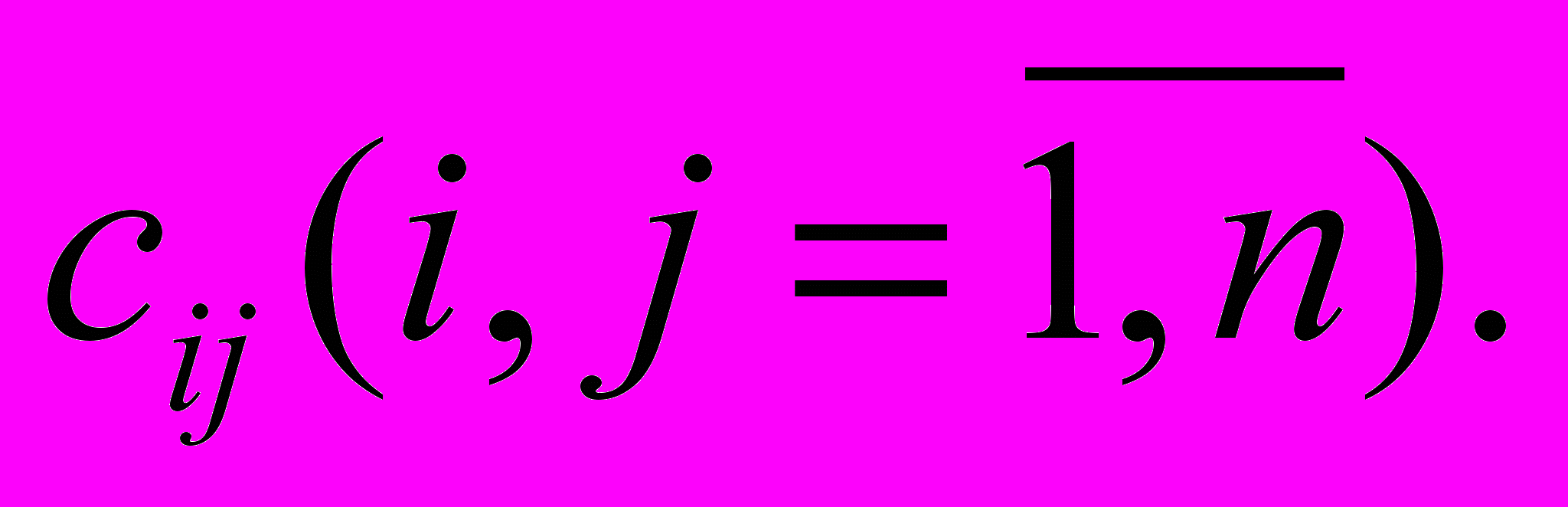Каждый кандидат может быть назначен только на одну работу, и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы, при котором суммарные затраты на выполнение работ минимальны.Пусть xij – переменная, значение которой равно 1, если i-тый кандидат выполняет j-тую работу, и 0 – в противном случае. Тогда условие о том, что каждый кандидат выполняет только одну работу, запишется в виде
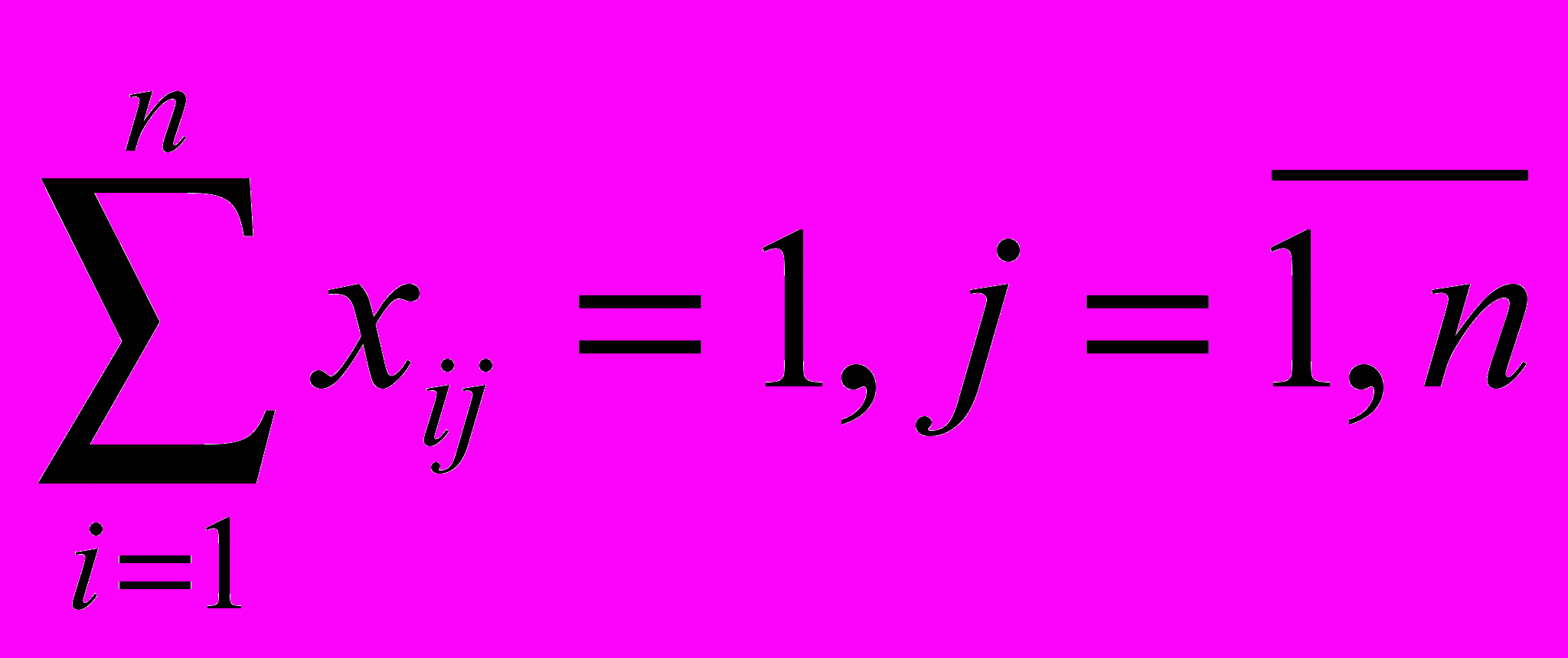(1)Условие о том, что каждая работа может выполняться только одним кандидатом, запишется в виде
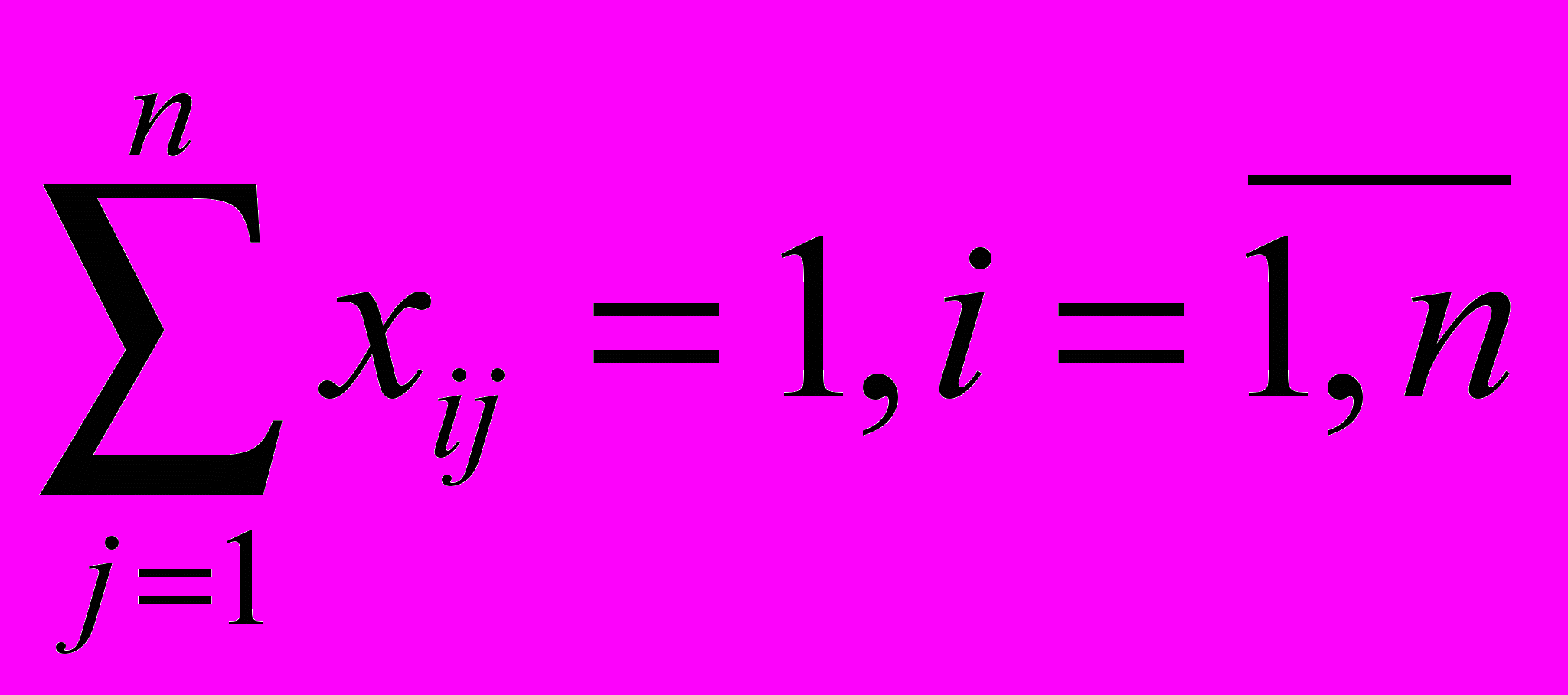(2)Целевая функция имеет вид
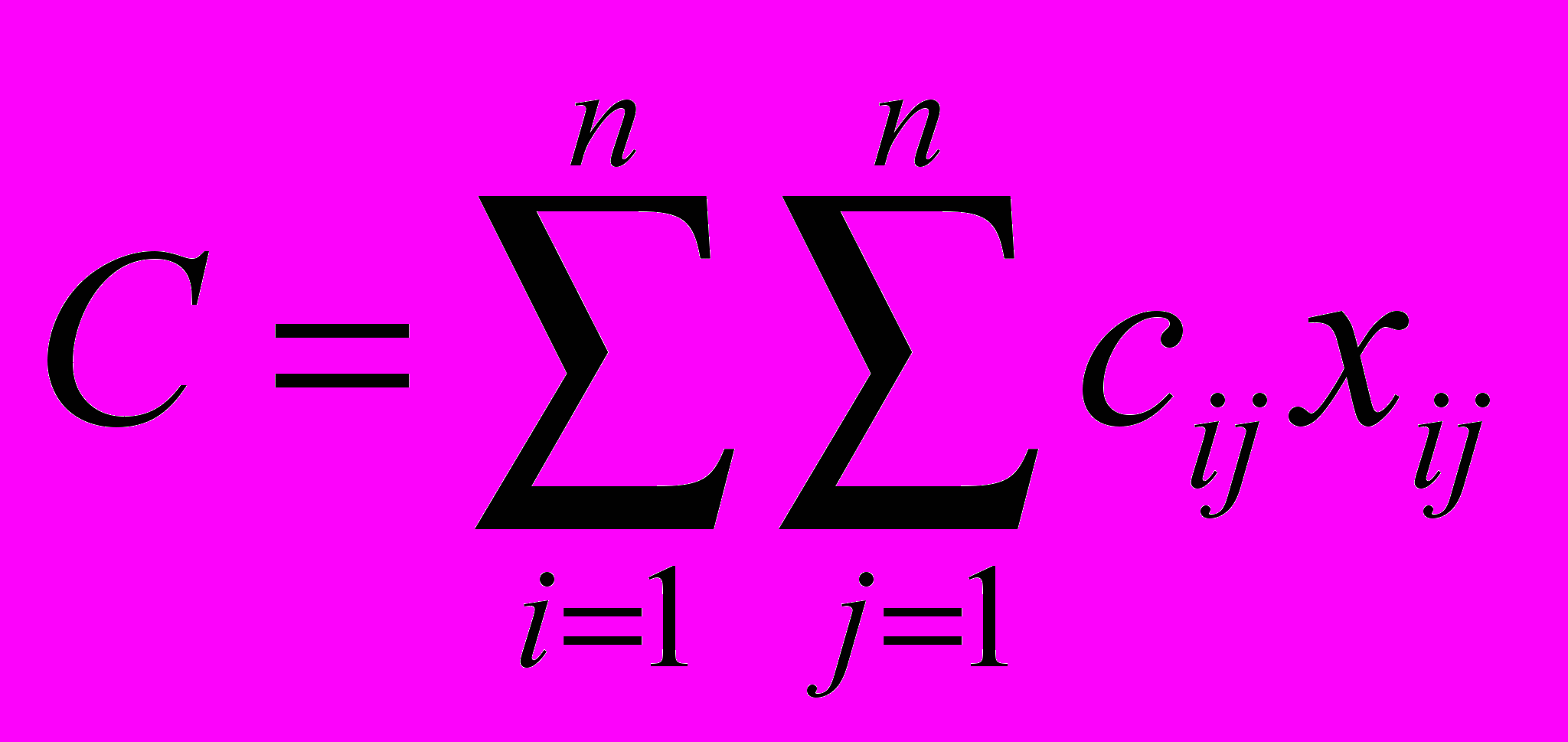(3)Как задачу линейного программирования, задачу о назначениях можно решать симплекс-методом. Однако существует специальный метод решения таких задач, называемый венгерским, который позволяет быстрее получить оптимальное решение.
Алгоритм венгерского метода состоит из следующих шагов:
- получение нулей в каждой строке;
- получение нулей в каждом столбце;
- поиск оптимального решения;
- поиск минимального набора строк и столбцов, содержащих все нули;
- перестановка некоторых нулей.
Авторы используют данный алгоритм для решения задачи о назначении институтом руководителей исследовательских проектов таким образом, чтобы общее время выполнения проектов было минимальным.
УДК 519.21
А.А. Абросимов
группа 882
Научный руководитель Я.В. Войтишек, к.т.н., доцент
КЛАССИЧЕСКИЕ ПАРАДОКСЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Как наука теория вероятностей зародилась в XVII благодаря распространению азартных игр среди знати. У игроков возникали различные вопросы в связи с логическим анализом схемы игр. Были сформулированы и решены первые задачи, имеющие прямое отношение к классической теории вероятностей, а дата их решения – 1654 год – считается датой рождения этой науки. Эти задачи получили названия «парадокс де Мере» и «парадокс раздела ставки». Первый заключался в неочевидности вероятностей различных комбинаций при игре в кости, а второй затрагивал вопрос честного раздела ставки между игроками в случае досрочного прекращения игры.
В начале XVIII века Академия наук в Санкт-Петербурге опубликовала статью, математические вычисления в которой, казалось, противоречили здравому смыслу. Парадокс получил название петербургского и состоял в следующем:
Некто Петр и Павел договариваются сыграть ряд партий в орла и решку или в подобную же игру, в которой шансы обоих партнеров равны, с условием, если Петр проигрывает n-1 первых партий и выигрывает n-ую, Павел выплачивает ему 2n франков и игра прекращается. Задача состоит в том, чтобы выяснить, какова должна быть ставка Петра, то есть та сумма, которую он до начала игры должен выплатить Павлу, чтобы игра получилась честной (то есть среднее значение выигрыша – его математическое ожидание – должно быть равно нулю). Однако данное естественное условие невыполнимо, какую бы конечную сумму денег не заплатил Петр Павлу.
В данной работе также рассмотрены частный и более приближенный к реальности случай «петербургской игры на квит», модель игры Жозефа Бертрана (при которой время игры принимается несущественным фактором), случай когда число партий достаточно велико, но установлено заранее, а также случай с не фиксированным числом партий.
УДК 51-77
Е.И. Павлюк
Группа 883
Научный руководитель: к.т.н., доцент, Я.В. Войтишек
ОСНОВНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ ЭКОНОМИКИ.
ОСНОВНАЯ ПРОИЗВОДСТВЕННАЯ ЗАДАЧА ТЕКУЩЕГО ПЛАНИРОВАНИЯ.
КРИТЕРИИ КАНТОРОВИЧА.
Моделирование – один из способов исследования экономических систем и процессов. Модель – образ реальной системы (объекта, процесса) в материальной или теоретической форме. Моделирование основывается на принципе аналогии, т. е. возможности изучения реального объекта (системы) не непосредственно, а опосредованно, через рассмотрение подобного ему и более доступного объекта (модели).
Пути повышения эффективности управления экономикой на разных уровнях – важнейшая проблема, стоящая перед специалистами в этой области. Поэтому в настоящее время серьезное внимание уделяется разработкам математических моделей различных экономических процессов и объектов, их анализу, прогнозированию и выработке управленческих решений на всех уровнях хозяйственной деятельности.
Цель этого исследования – проанализировать и рассмотреть примеры применения линейных моделей в экономических процессах.
С помощью теории двойственности в терминах оценок можно установить для каждой такой модели критерии оптимальности ее плана. Для основной производственной задачи такой критерий дал Л.В. Канторович. В некоторых частных случаях использование критерия оптимальности плана дает возможность находить решение задачи.
Предметом исследования является основная производственная задача текущего планирования, рассматриваются один из ее вариантов: задача о выпуске продуктов в заданных размерах. Приводится математическая формулировка задачи, задача представляется как для частного случая, так и в общем виде. Решение основывается на применении критериев оптимальности двойственных задач.
Общий вид задачи о выпуске продуктов в заданных размерах имеет вид:
В процессе производства участвуют n продуктов (ингредиентов) и применяются m технологических способов T1,T2,…,Tm. Определено выпускаемое количество единиц продукта при однократном применении каждого технологического способа. Выпуск каждого продукта должен быть не меньше определенного количества единиц. Известны денежные затраты при однократном применении каждого технологического способа. Требуется определить такие интенсивности использования технологических способов, при которых каждый продукт выпускается в объеме не меньшем указанного, а суммарные денежные затраты достигают наименьшего значения.
УДК 51-77
Косухина М. А.
Группа: 362
Научный руководитель: проф. Галилеев М.М.
АППРОКСИМАЦИЯ ЦИКЛИЧЕСКИХ ПРОЦЕССОВ C ПОМОЩЬЮ ИНТЕГРИРОВАННОГО МАТЕМАТИЧЕСКОГО ПАКЕТА MAPLE
Особенностью моделирования циклов экономической динамики является придание формализуемым функциям дискретной формы. Математическое описание циклов позволяет решать ряд важных задач: изучение внутренних процессов данного явления; моделирование и изучение поведения параметров циклов под воздействием меняющихся значений факторов; использование полученных результатов для перспективного и текущего планирования.
В рамках данной работы рассматривается аппроксимация данных макроэкономической динамики на примере США. Для моделирования динамики ВВП используется уравнение макроэкономической динамики, полученное А.А.Акаевым, которое имеет вид:
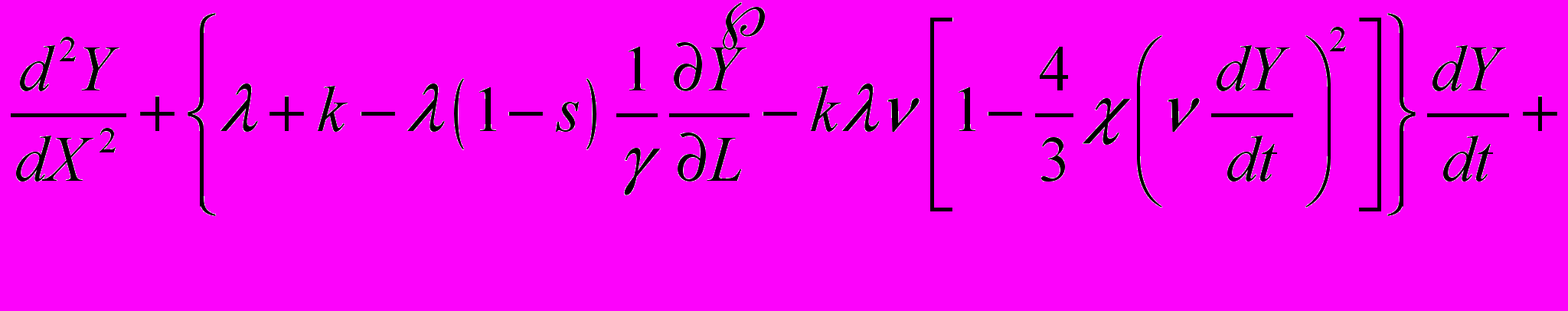
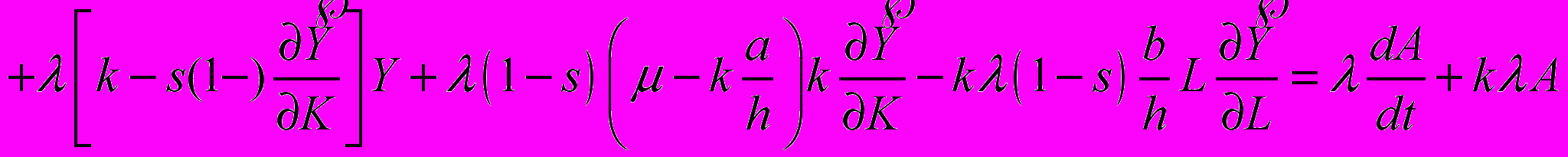
Правая часть уравнения представляет собой функцию аппроксимирующую статистические данные по инвестициям в экономику США. Чем точнее будут описаны инвестиции, тем точнее получится прогноз ВВП. Для аппроксимации данных использовался пакет приближения кривых CurveFitting, интегрированного математического пакета Maple 11, в который входит ряд функций: функция реализации метода наименьших квадратов LeastSquares, функция полиномиальной аппроксимации PolynomialInterpolation, функция рациональной аппроксимации RacionalInterpolation и др.
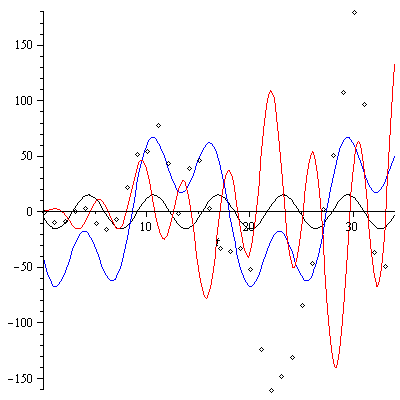
Здесь ˚ фактические данные,- различные функции аппроксимации
Верификация математической модели показывает, что используемые аппроксимации инвестиций позволяют получить результаты, при которых максимальное отклонение расчетного значения ВВП от фактического не превышает 5%.
УДК 519.7
С.И.Гоппов,
Гр. 3661
Научный руководитель: доц. Сергеев А.Н.
НЕЧЁТКАЯ ЛОГИКА В СИСТЕМАХ УПРАВЛЕНИЯ. НЕЧЁТКОЕ МОДЕЛИРОВАНИЕ В СРЕДЕ MATLAB
Теория нечетких множеств (fuzzy sets theory) ведет свое начало с 1965г., когда профессор Лотфи Заде (Lotfi Zadeh) из университета Беркли опубликовал основополагающую работу “Fuzzy sets” в журнале “Information and Control”. Концепция нечеткого множества зародилась у Заде «как неудовлетворенность математическими методами классической теории систем, которая вынуждала добиваться искусственной точности, неуместной во многих системах реального мира, особенно в так называемых гуманистических системах, включающих людей». В его работе понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0..1], а не только 0 или 1. Такие множества были названы нечеткими. Также были предложены различные логические операции над нечеткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечеткие множества.
Основанные на этой теории методы построения информационных моделей существенно расширяют традиционные области применения компьютеров и образуют самостоятельное направление научно прикладных исследований, которое получило специальное название - нечеткое моделирование.
Актуальность новой технологии обусловлена тенденцией увеличения сложности математических и формальных моделей реальных систем и процессов управления, связанная с желанием повысить их адекватность и учесть все большее число различных факторов, оказывающих влияние на процессы принятия решений. Традиционные методы построения моделей не приводят к удовлетворительным результатам, когда исходное описание подлежащей решению проблемы заведомо является неточным или неполным. С другой стороны, стремление получить всю исчерпывающую информацию для построения точной математической модели сколько-нибудь сложной реальной ситуации может привести к потере времени и средств, поскольку это может быть в принципе невозможно.
В подобных случаях наиболее целесообразно воспользоваться методами, которые специально ориентированы на построение моделей, учитывающих неполноту и неточность исходных данных. Именно в таких ситуациях технология нечеткого моделирования оказывается наиболее конструктивной, поскольку за последнее десятилетие на ее основе были решены сотни практических задач управления и принятия решений.
В настоящей работе приведены примеры решения практических задач с использованием пакета прикладных программ, входящих в состав среды MATLAB - Fuzzy Logic Toolbox, который позволяет создавать системы нечеткого логического вывода и нечеткой классификации. Базовым понятием Fuzzy Logic Toolbox является FIS-структура - система нечеткого вывода (Fuzzy Inference System). Система MATLAB позволяет выполнять весь комплекс исследований по разработке и применению нечетких моделей. Именно по этим причинам система MATLAB была выбрана для реализации теоретических концепций нечетких множеств и процедуры нечеткого вывода.
УДК 519.23
Юлия Гафарова группа7282
Анастасия Александрова группа 7282
Научный руководитель: канд. физ.-мат.наук, доцент, Гончар Л.И.
АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
Показатели многих явлений в экономике и социальной жизни изменяются во времени. Числовые данные образуют временной ряд, который выражает зависимость показателя от времени и имеет вид либо таблицы, либо графика.
В экономике и социологии часто встречаются дискретные ряды, в которых значения показателя фиксируется лишь для некоторых дискретных моментов.
Временной ряд часто может рассматриваться как реализация случайного процесса, причём для решения практических задач достаточно знать следующие его числовые характеристики: математическое ожидание, дисперсия, автокорреляционная функция.
Основные задачи анализа временных рядов.
1.Определение числовых характеристик ряда;
2.Разложение уровней ряда на составляющие: либо а)случайные и неслучайные, либо б)основную тенденцию (тренд ряда), короткопериодические колебания, быстрые и хаотические изменения;
3. Сглаживание ряда. Для выделения тренда широко используют 3 метода: наименьших квадратов, скользящей средней, экспоненциального сглаживания. Решения задач выделения тренда и сглаживания практически совпадают;
4. Выявление факторов, влияющих на уровни ряда. Оценка их относительного значения и количественной связи с уровнями ряда;
5.Прогнозирование ряда. Для него необходимо выявить основные факторы, влияющие на его ход и количественно оценить их влияние. Прогнозирование ряда может проводиться различными методами: либо прогнозирование трендовых значений ряда, либо путём экстраполяции аналитической функции времени, либо экспоненциального сглаживания;
6. Анализ связей между временными рядами различных показателей. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда.
Прогноз будущих значений временного ряда используется для эффективного принятия решений в рамках моделируемого процесса.
УДК 519.23
С.В. Ушерович
Группа 7281
Научный руководитель: к.ф.-м.н., доцент, Гончар Л.И.
ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Системы массового обслуживания (СМО) встречаются во многих областях производства и быта. Каждая СМО имеет каналы обслуживания. Время обслуживания и характер потока заявок случайны. При этом СМО может моделироваться как стационарный пуассоновский поток, который выражается формулой
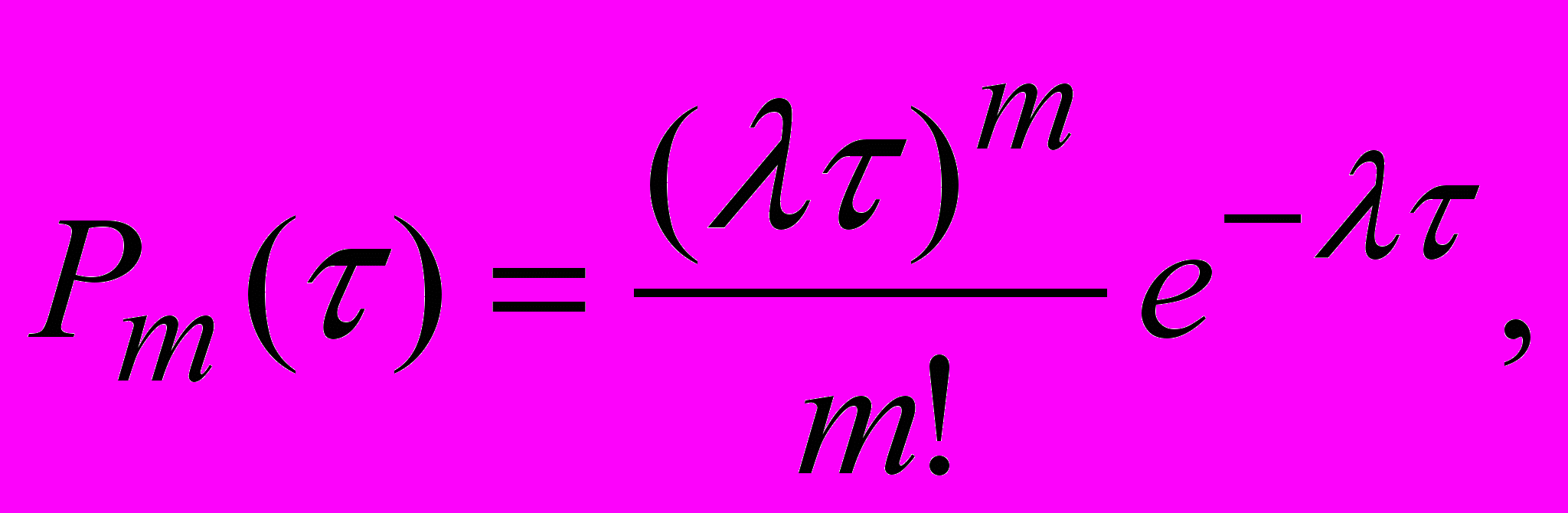где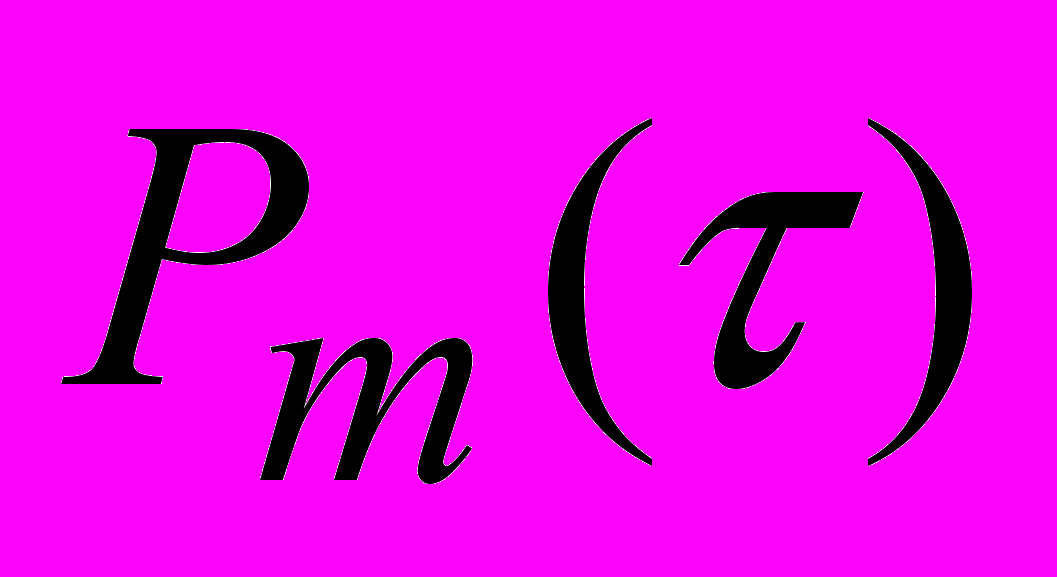 
– вероятность поступления m заявок за время τ; λ=const – плотность, или интенсивность, потока заявок, т.е.среднее число заявок, поступивших за единицу времени; a=λτ – математическое ожидание числа заявок, поступивших за время τ.Задача теории массового обслуживания – рациональная организация работы СМО для максимизации её эффективности. К показателям эффективности относят производительность, время обслуживания заявки, которое распределено по показательному закону:
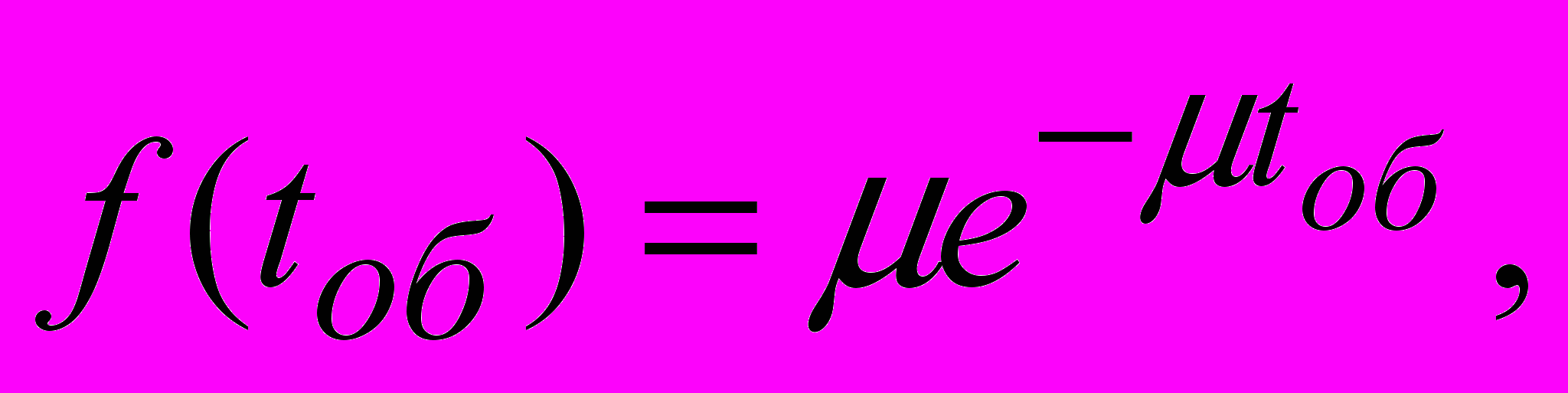где tоб≥0; μ – величина, обратная среднему времени обслуживания одной заявки.Полное статистическое описание функционирования СМО задается вероятностями Pi(t) каждого из её возможных состояний. Эти вероятности в общем случае есть функции времени. В этом случае переходы системы из одного состояния в другое образуют так называемый марковский процесс. Зная вероятности Pi(t), нетрудно получить формулы для всех других показателей функционирования СМО.
При нестационарных пуассоновских потоках значения Pi(t) всё время меняются, и вероятности могут быть получены как функции времени численным решением на ЭВМ уравнений, описывающих переход СМО из одного состояния в другое при любых заданных законах изменения λ(t), μ(t) и v(t)(величины, обратной среднему значению времени ожидания)
УДК 330.45, 519.872.2
А.Н.Драбушева
Группа 181
Научный руководитель: доктор физ.-мат. наук профессор И.Е.Погодин
ИССЛЕДОВАНИЕ РАБОТЫ СМО С ОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ ПРИ НАЛИЧИИ ПЕРЕРЫВА (КРИЗИСА)
Работа многих систем моделируется системами массового обслуживания (СМО) из n однотипных устройств, каждое с пропускной способностью ν, при L местах для ожидания. Здесь рассматриваются способы учета перерывов (продолжительностью τ) в работе СМО, которые способны изменить дальнейшую деятельность такой, принципиально статистической, системы, вплоть до ее полной необратимой остановки.
Если условно разбить время работы СМО на четыре режима: I-стабильный (до перерыва), II-затухания (во время перерыва), III-первичного восстановления (сразу после перерыва), IV-окончательного восстановления стабильного режима I, то моделирование режима III наталкивается на ряд трудностей. В частности: явный вид зависимости поступления заявок µ(t) неизвестен, зависят от времени коэффициенты дифференциальных уравнений системы Колмогорова «гибели и рождений»; причем при некоторых дополнительных предположениях о режиме III эта система становится существенно нелинейной. Поэтому решение уравнений Колмогорова в III режиме можно искать в виде степенных рядов при некоторых априорных предположениях, неизбежно накладывающих ограничения на область применения соответствующих моделей, либо задавая пробный вид µ(t) и строго отрабатывая его с помощью встроенных возможностей пакета «MATHCAD»:
1. «Гидродинамический подход» накопления и обработки заявок ограничен достаточно большой интенсивностью их поступления извне.
2. «Квазистатический самосогласованный подход» предполагает, что при малой скорости изменения условий работы СМО, она успевает входить в квазистабильные режимы при текущих µ(t), которые рассчитываются стандартным образом. Тогда
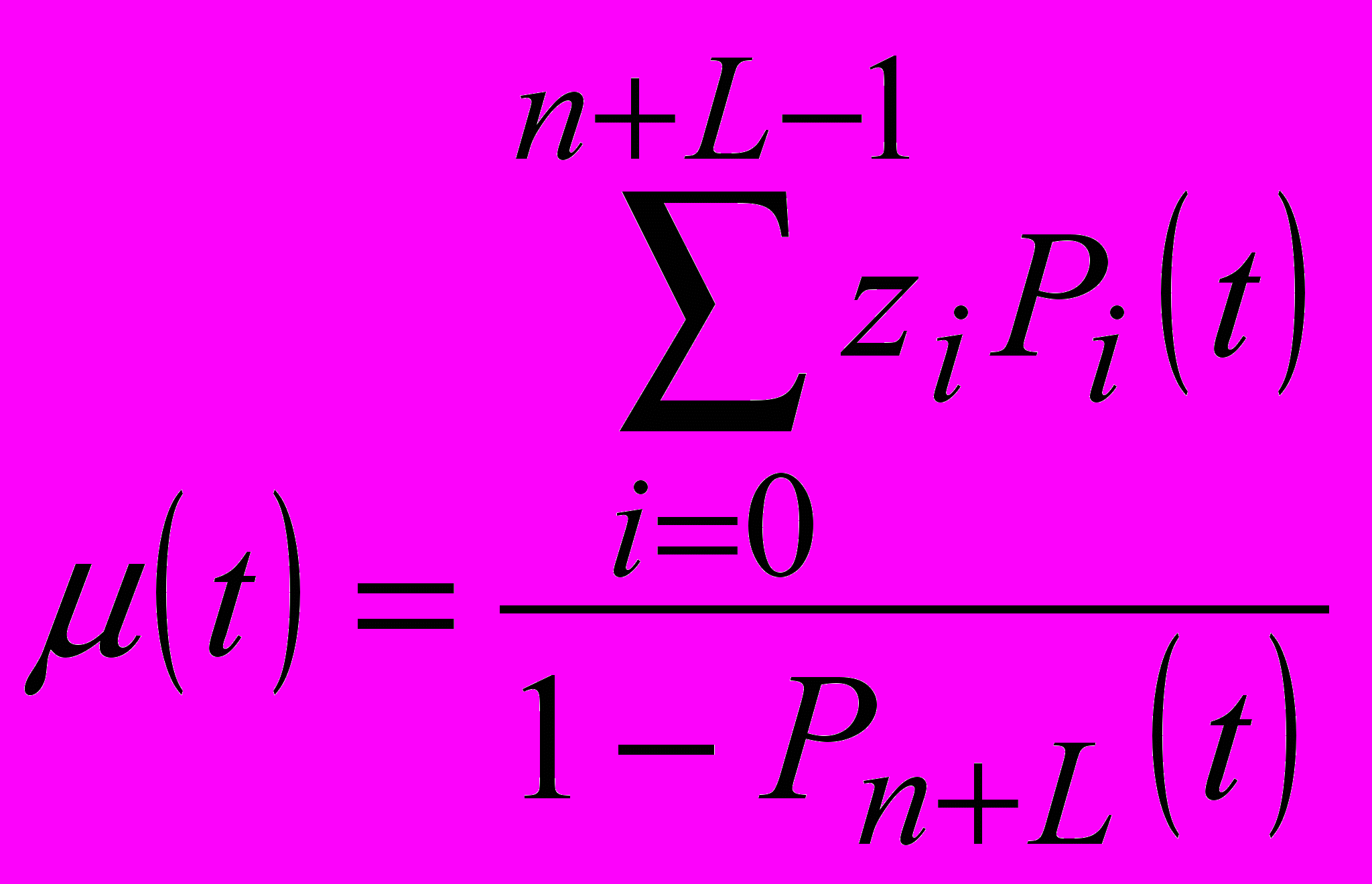подставляется в систему уравнений Колмогорова для нахождения вероятностей {
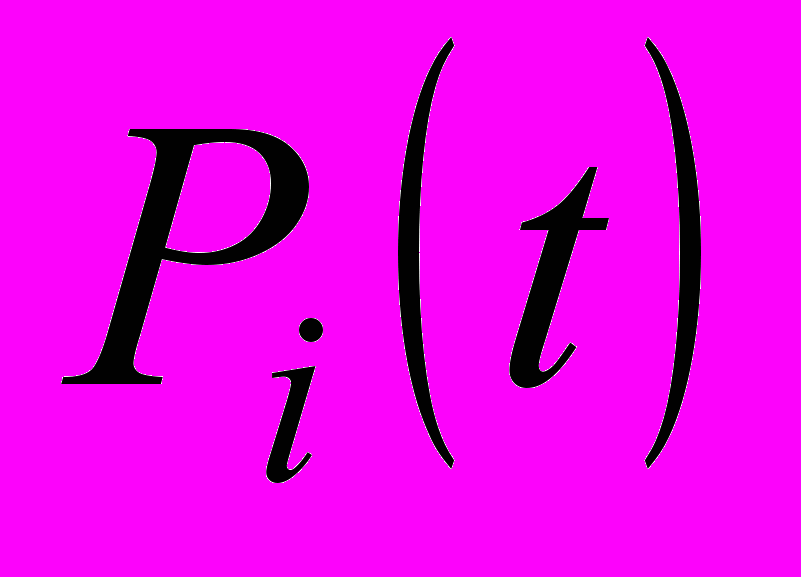} (i=0÷(n+L)) в виде рядов Маклорена по степеням t. 3. Ещё более условный «модельный» подход к решению задачи может включать предположения о явном виде µ(t), например:
, 
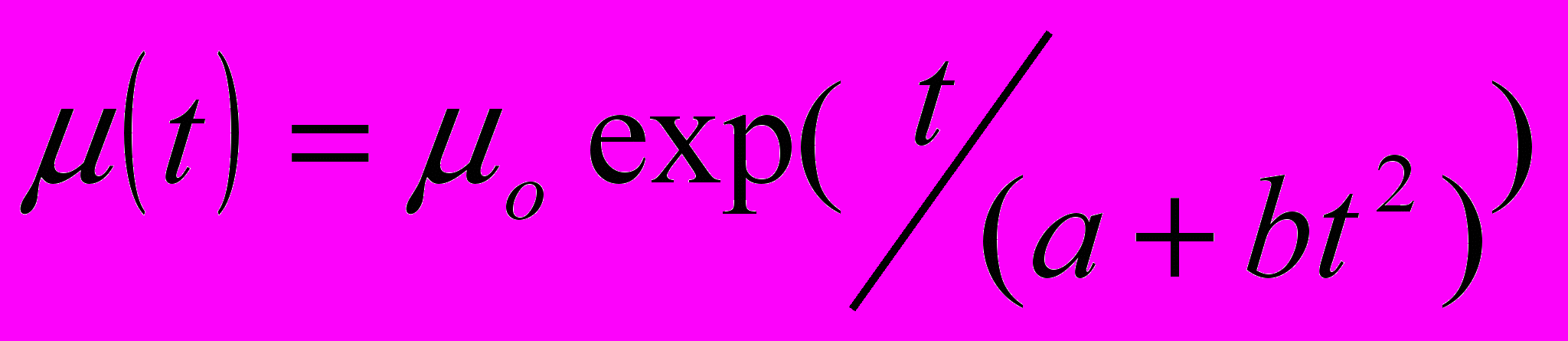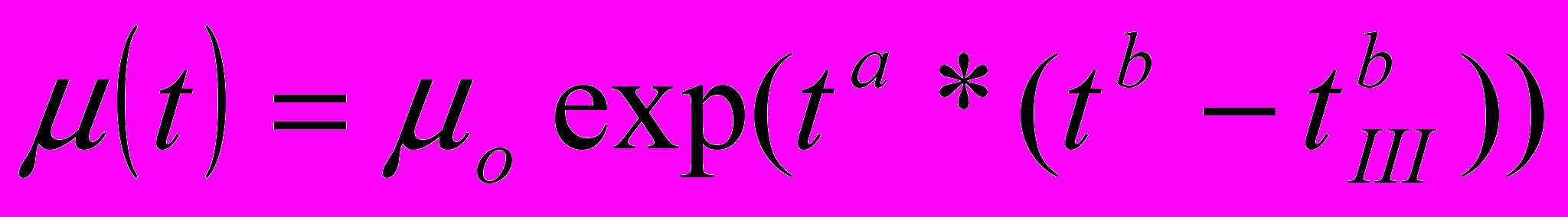, где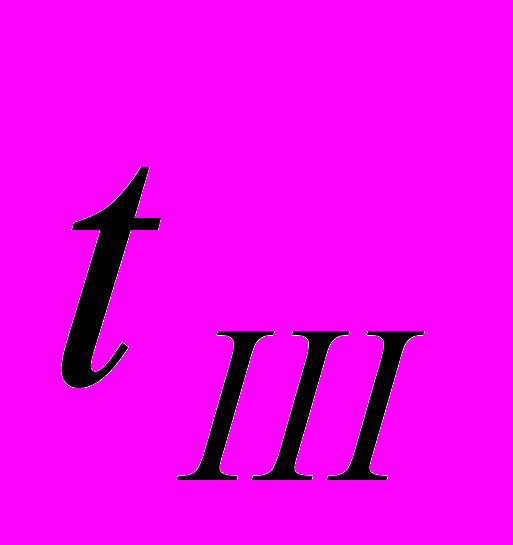 
- длительность режима III, a и b- числовые параметры.С учетом изложенных особенностей задачи были проделаны аналитические и численные расчеты для СМО с малым числом состояний, которые позволили исследовать влияние параметров системы и потока заявок на практически важные характеристики (вероятности простоя, ожидания и отказа в обслуживании).
УДК 519.23
Горячева В.Б.
Группа 7282
Научный руководитель: канд. физ.-мат.наук доцент Гончар Л.И.
СТАТИСТИЧЕСКОЕ ИММИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
Имитационное моделирование, при котором воспроизводится случайные явления, называется статистическим имитационным моделированием (СИМ). Под СИМ понимают построение имитационной модели существующего или гипотетического объекта, учитывающей случайные явления, и проведение экспериментов на этой модели. Главное преимущество данной модели: она позволяет экономить огромные средства и много времени при разработке и совершенствовании сложных технических и организационно-технических объектов. Существует определенный алгоритм выполнения имитационного моделирования:
1)Установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства.
2)Задать законы распределения вероятностей для ключевых параметров модели.
3)Провести компьютерную имитацию значений ключевых параметров модели.
4)Рассчитать основные характеристики распределений исходных и выходных показателей.
5)Провести анализ полученных результатов и принять решение.
Как работает СИМ, рассмотрим на примере моделирования процесса обслуживания покупателей одним продавцом. Формулируем основную проблему: покупатели, которые приходят в магазин, часто остаются без внимания продавца. Наша задача: минимизировать время простоя продавца и максимизировать число покупателей. В этом случае в качестве критериев могут быть использованы:
Среднее время ожидания продавца:
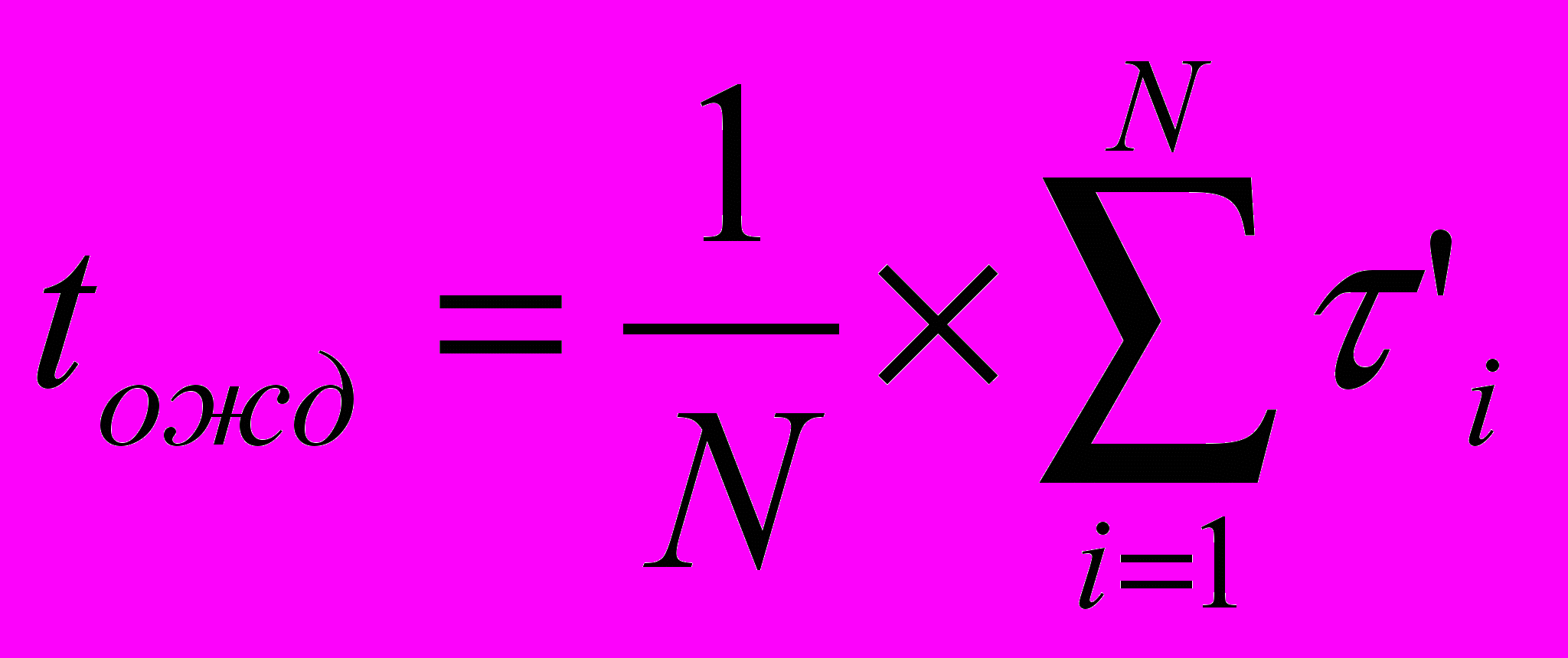, где N= общее число покупателей, 
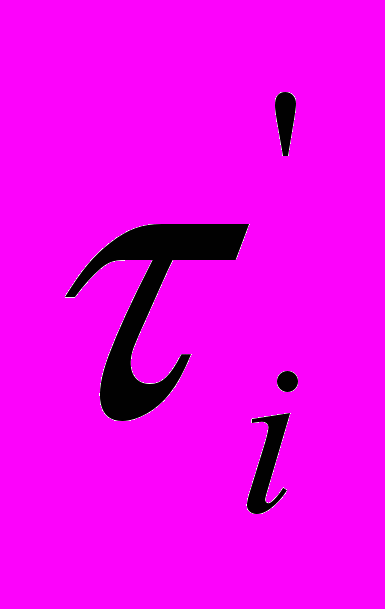- время ожидания обслуживания i-м покупателем. Процент загрузки продавца:
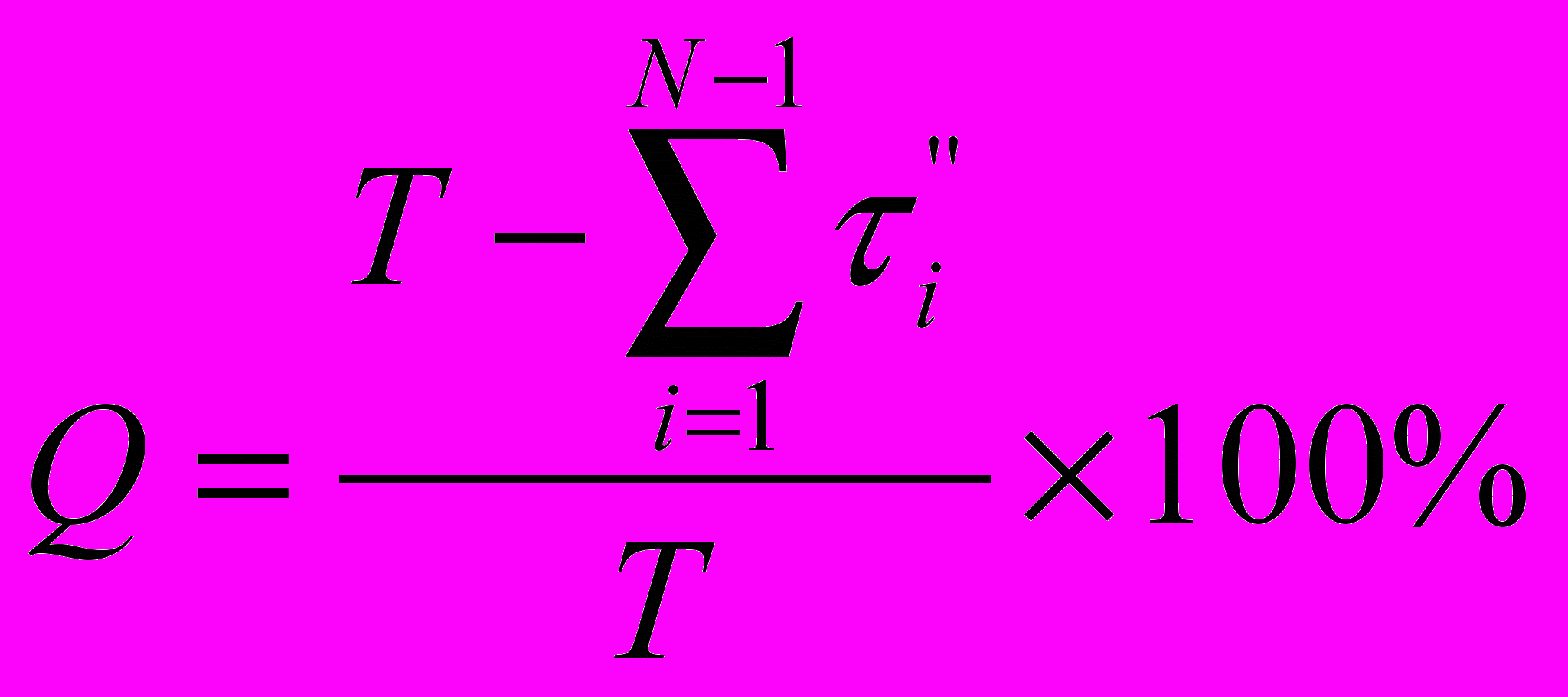, где T-моделируемое время работы магазина, 
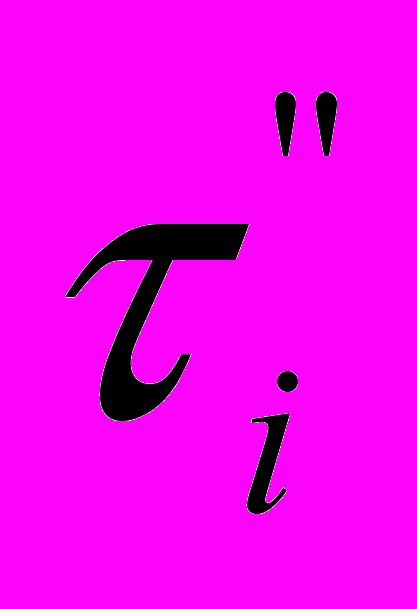- время простоя продавца.К недостаткам рассмотренного подхода следует отнести: трудность понимания и восприятия менеджерами имитационных моделей; при разработке реальных моделей может возникнуть необходимость привлечения специалистов или научных консультантов со стороны; относительную неточность полученных результатов и др.
В настоящее время имитационное моделирование является основой для создания новых технологий управления и принятия решений в сфере бизнеса, а развитие вычислительной техники и программного обеспечения делает этот метод все более доступным для широкого круга специалистов-практиков.
УДК 51-77
Е.Лантус, К.Соловьёва
группа 7282
Научный руководитель: канд. физ.-мат.наук, доцент, Гончар Л.И.
МОДЕЛИ УПРАВЛЕНИЯ КРЕДИТНЫМИ РЕСУРСАМИ ПРЕДПРИЯТИЯ
В рыночной экономике предприятие самостоятельно определяет рациональные варианты всех составляющих производственно-финансовой деятельности. При этом одной из экономических оценок эффективности вариантов мероприятий является прибыль предприятия, остающаяся в его распоряжении. Потому основной задачей в условиях рынка является повышение эффективности функционирования предприятия путем оптимизации использования его ресурсов, в том числе финансовых, и разработка наиболее рациональной производственной программы. Для достижения этой цели руководство предприятия может принимать решение о реконструкции или о переходе на выпуск новой продукции, следовательно, возникает потребность в дополнительных инвестициях. Проблема поиска наиболее эффективных условий инвестирования, учитывающих оптимальную производственную программу предприятия, имеет немаловажное значение.
Основной целью, которая ставится при моделировании, является вывод оптимального решения задачи получения предприятием максимальной прибыли как важнейшей задачи предприятия, путем оптимизации производственной программы в условиях ограничений на время использования оборудования, материальных и финансовых ресурсов, а также в условиях использования кредита для пополнения оборотных средств и реализации инвестиционных программ. Кроме того, важным является решение задачи минимизации срока окупаемости проекта с целью сделать кредит более доступным для предприятия и сократить издержки на обслуживание долга.
Модели управления кредитными ресурсами предприятия построены на основе базовой модели, которая состоит в решении задачи выбора оптимальной производственной программы в простейшем случае, когда в модель включены ограничения по производственным мощностям, материально-сырьевым ресурсам, спросу на продукцию, и она не включает условия использования финансовых ресурсов.
На практике используются следующие модели:
- Модель расчета объема кредитования оборотных средств предприятия.
2. Модель расширения производства с учетом использования кредита.
3. Модель перепрофилирования производства на выпуск новых изделий.
4. Модель оценки времени и объемов кредитования предприятий в условиях расширения производства.
УДК 519.24
Волошина К. Р.
группа 3581
Научный руководитель: к.э.н., доцент, С.Е.Игнатова
ОЦЕНКА ДОСТОВЕНОСТИ РАЗЛИЧИЙ ДЛЯ ЗАВИСИМЫХ И НЕЗАВИСИМЫХ ВЫБОРОК С ПОМОЩЬЮ Т-КРИТЕРИЯ СТЬЮДЕНТА
t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез. Одним из главных достоинств критерия является широта его применения.
Формула t – критерия Стьюдента для несвязных выборок имеет вид:
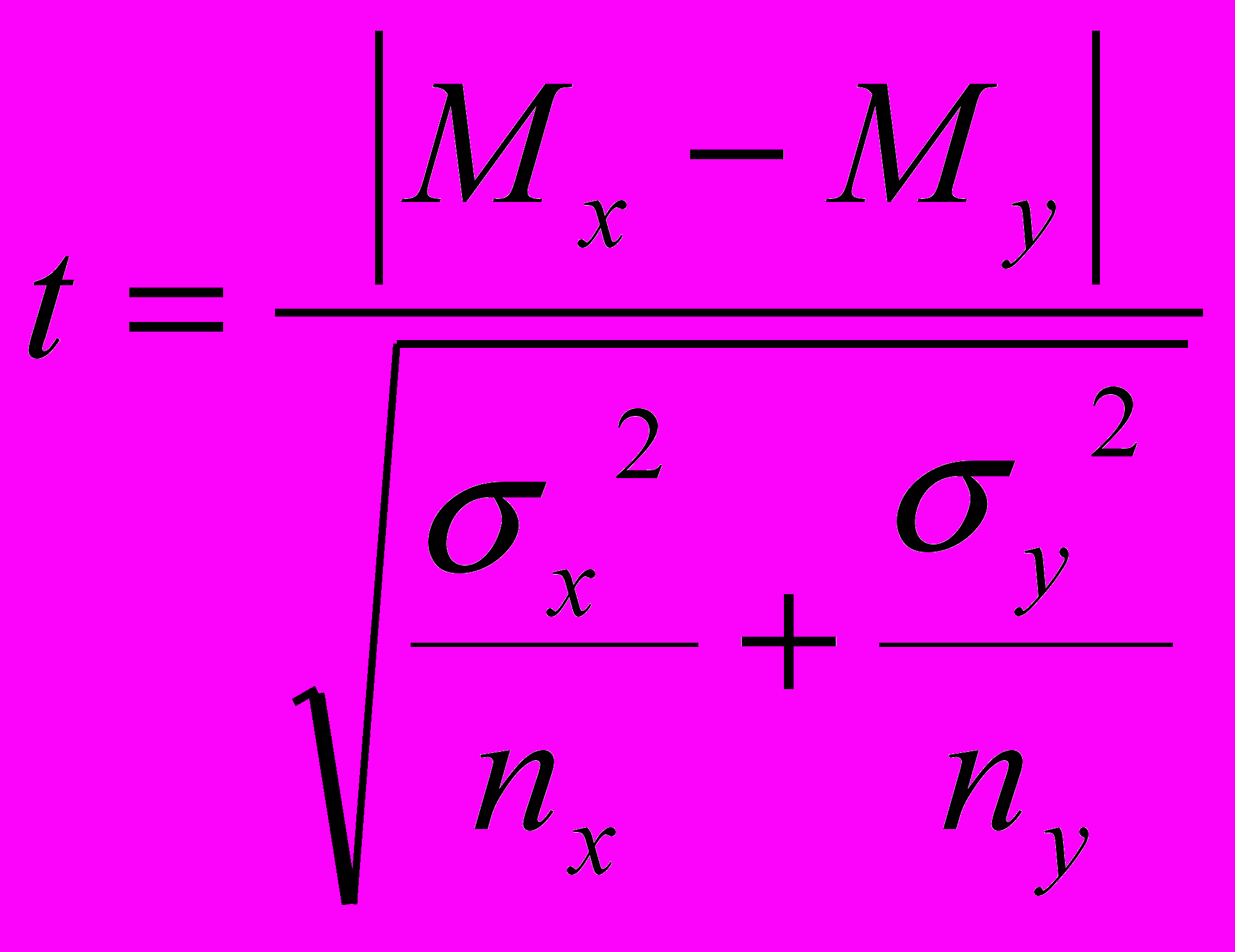
где M – среднее арифметическое значение, σ – стандартное отклонение.
Постановка задачи заключается в следующем. Студенты в двух различных группах в течении года занимались по двум различным методикам. Известно, что начальный уровень в этих группах был примерно одинаков. В конце учебного года были сделаны замеры показателей интеллекта.
Подстановка значений в формулу дает следующий результат:
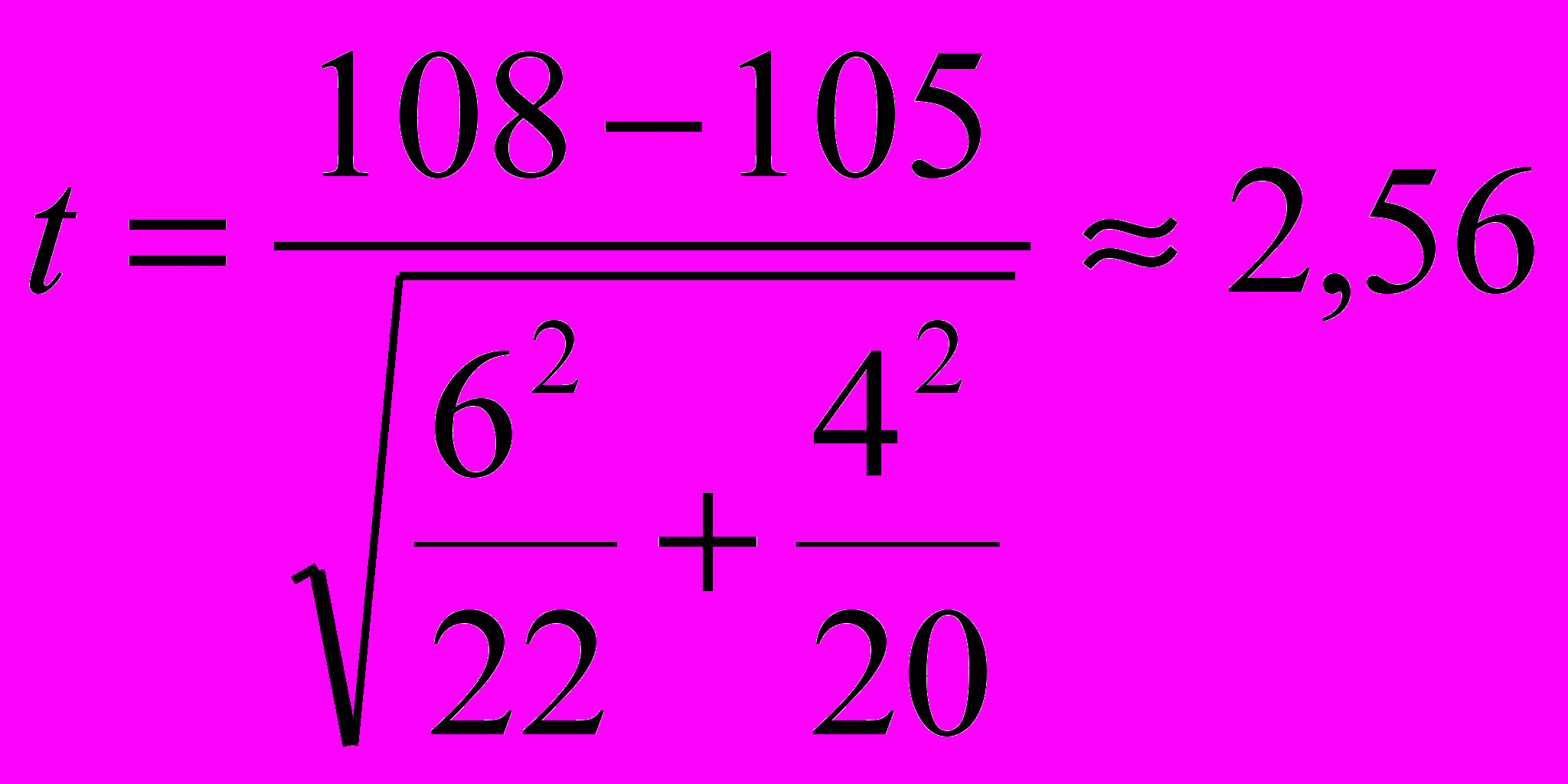
tэмп > tкр, следовательно мы можем уверено отвергнуть гипотезу Н0 и констатировать, что обнаружены статистически значимые различия между показателями умственного различия у представителей разных групп.
Критерий для связанных выборок имеет следующую форму:
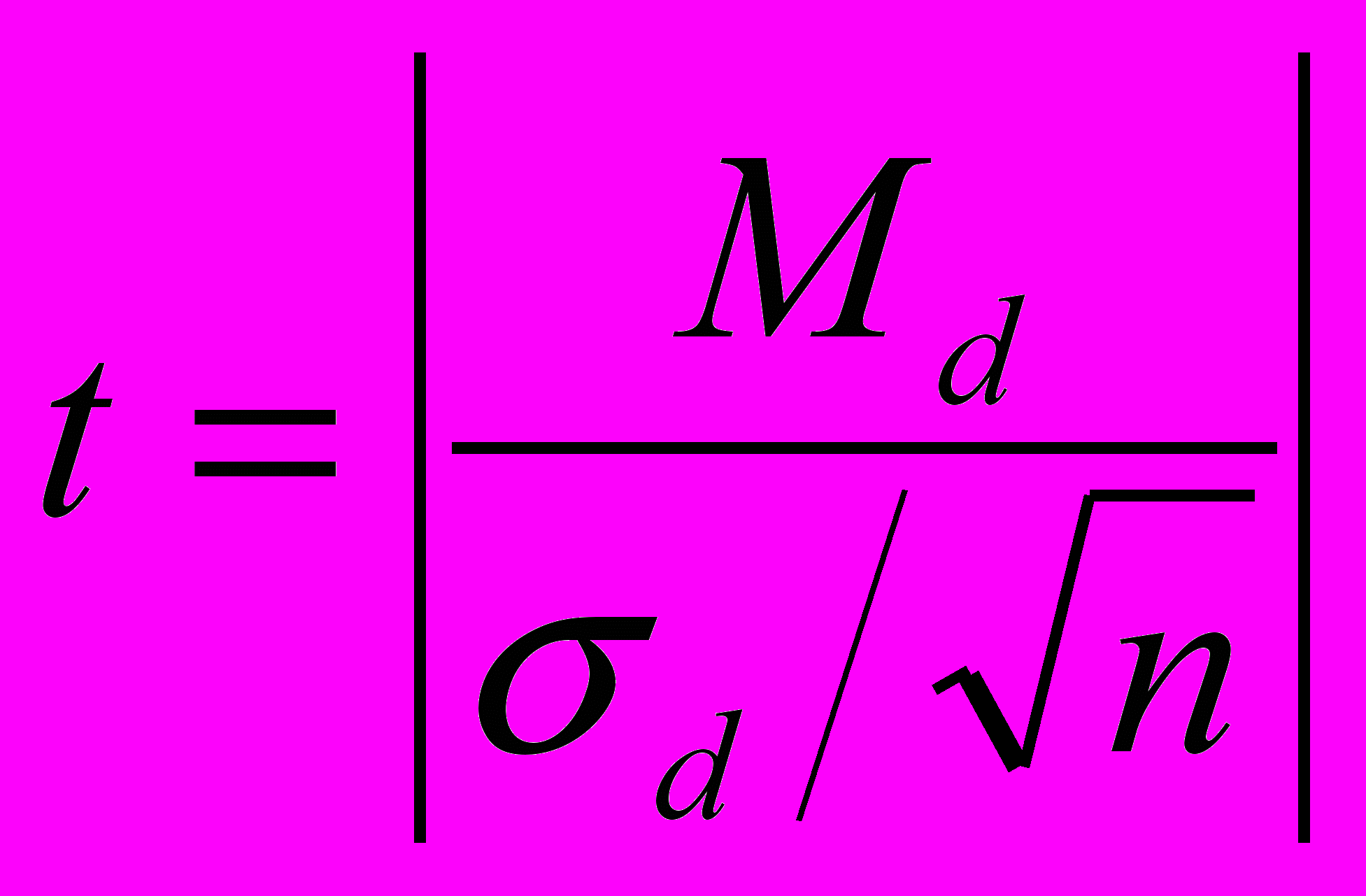
Пусть перед началом первого учебного года был измерен уровень интеллекта у группы студентов. В начале второго года при помощи параллельной методики он был измерен вновь и были исключены результаты тех студентов, которые не подвергались обследованию на фазе заключительных срезов.
В нашем примере tкр для df = 11 составляет 2,201 при р ≤ 0,05. Таким образом, tэмп > tкр (р ≤ 0,05), а значит мы можем принять на уровне статистической значимости гипотезу о достоверности сдвига значений интеллекта за год обучения.
УДК 519.24
А.М. Анищенкова
Н.С. Черевань
гр. 3581
Научный руководитель: к.э.н., доцент, C.Е. Игнатова
СТАТИСТИЧЕСКИЕ МЕТОДЫ В ИССЛЕДОВАНИИ ДОХОДОВ НАСЕЛЕНИЯ
Используя статистические данные федеральной службы государственной статистики РФ о распределении населения по размеру среднедушевого денежного дохода на конец 2009:
| № группы домашних хозяйств | Среднедушевой доход в месяц, руб. | Численность населения, % |
| 1 | До 2000 | 1 |
| 2 | 2000 - 4000 | 6,5 |
| 3 | 4000 - 6000 | 10,3 |
| 4 | 6000 - 8000 | 11,1 |
| 5 | 8000 - 10000 | 10,4 |
| 6 | 10000 - 15000 | 20,4 |
| 7 | 15000 - 25000 | 21,8 |
| 8 | Более 25000 | 18,5 |
Нами было получено значение среднего квадратического отклонения, равное 9790,13. Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности; оно показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения. Чем меньше значение среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной является средняя величина. Был найден коэффициент вариации, равный 63,7%. Коэффициент вариации используют также как характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Таким образом можно сделать вывод, что распределение доходов среди населения происходит неравномерно.
Литература:
- В.Е. Гмурман Теория вероятностей и математическая статистика: М.: «Высшая школа», 2001.
- Федеральная служба государственной статистики «Распределение населения по размеру среднедушевого денежного дохода»
УДК 51-77
Юдаев А.И.
группа 6171
Научный руководитель: старший преподаватель Петросян Г.А.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ И КОРРЕЛЯЦИОННЫЕ КОЭФФИЦИЕНТЫ КАК АПРОБИРОВАННЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ КОЛИЧЕСТВЕННОГО АНАЛИЗА В СОЦИОЛОГИИ.
В последнее время в социологии наметилась тенденция использования не только качественных, но и количественных методов, опирающихся на математический аппарат, увеличивающих тем самым объективность и достоверность получаемых результатов социологического исследования. Это закономерный этап в развитии социологии, так как ученые убедились в необходимости сочетания качественного и количественного анализа, а так же применения математико-статистических методов.
Дело в том, что математические методы дают нам возможность не только количественного подсчета тех или иных величин, но и выявления между ними скрытых до этого взаимосвязей, или так называемых корреляций.
Рассмотрим непосредственно сам термин: «корреляция» - показатель наличия зависимости двух или более переменных, при этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Корреляционная зависимость не является абсолютно точной. В ней может отражаться множественность как причин, так и следствий.
Корреляционные зависимости часто наблюдаются между многими признаками элементов нашего социума – социальными, экономическими, а также между различными политическими процессами. В рамках именно социологического знания еще Эмиль Дюркгейм уделял большое внимание корреляциям. В частности, в своей работе «Самоубийство» он обнаружил и описал корреляционную зависимость между числом самоубийств и временем года. На данный момент известно множество корреляционных зависимостей, которые хорошо изучены. Так, например, уровень доходов, как правило, зависит от уровня образования, есть корреляция между социальным и экономическим статусом и.т.д.
В нашем исследовании мы затронули несколько интересующих нас аспектов бюджета времени современного студента, и одним из них является взаимосвязь времени, проводимого студентом в социальных сетях и времени, проводимого студентом за компьютером в целом. Результаты данного исследования были интерпретированы не только с помощью математического аппарата, но и с учётом специфики изучаемого социального явления, ведь только в этом случае мы можем говорить об объективности полученных выводов и суждений.
УДК 519.243
Зданович Е.А., Оробец П.В.
Группа 1082
Научный руководитель: к.э.н., профессор Петрова Л.Ф.
Экспертные оценки и их применение в учебном процессе
Метод экспертных оценок позволяет обрабатывать количественные оценки объектов или явлений, которые непосредственно измерены быть не могут. К наиболее употребительным приемам относят ранжирование, парное сравнение, последовательное сравнение. Чаще всего при упорядочении объектов по некоторому признаку применяют ранжирование, т.е. числовое представление объектов в виде натуральных чисел. Самому предпочтительному объекту ставят в соответствие 1, следующему 2 и т.д. Эти числа называются рангами.
Для эквивалентных объектов удобно назначать одинаковые ранги, равные среднему арифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называются связанными. Они могут оказаться дробными числами.
При парном сравнении происходит установление предпочтения объектов при сравнении всех возможных пар. При этом возможны отношения либо порядка, либо порядка и эквивалентности, что доводится до сведения экспертов.
Полученные результаты обрабатываются с помощью математического аппарата. В частности, рассматриваются показатели обобщенного мнения, одним из которых является сумма рангов. Наиболее важными считаются объекты, для которых этот показатель наименьший. Также рассматриваются показатели степени согласованности мнений экспертов.
Авторы доклада провели социологический опрос среди студентов II курса специальности «Менеджмент организации». Целью опроса было оценить восприятие студентами преподавания предметов учебной программы: «Экономика предприятия», «Информатика», «Правоведение», «Современные технологические системы», «Математика», «Иностранный язык», «Физкультура», «Социология и психология управления». Студентам было предложено оценить по 100-балльной системе благоприятный психологический климат на занятиях и оценить качество преподавания перечисленных выше дисциплин. Данные критерии, с точки зрения авторов, могут быть общими для перечисленных предметов. Проведенная экспертиза и статистический анализ полезны для студентов и для преподавателей, так как с точки зрения докладчиков, преподаватели смогут не только оценивать работу студентов, но и иметь представление о том, как студенты воспринимают их работу.
УДК 378.147
Крышко М.М.
гр. 5091
Научный руководитель: доц. А.Н.Сергеев
MathCAD-ЛЕКЦИИ ПО ВЫСШЕЙ МАТЕМАТИКЕ
MathCAD — программа для выполнения и документирования инженерных и научных расчётов. Появившись в 1986 году, MathCAD впервые среди программ подобного рода использовал наборную математическую нотацию, совмещённую с автоматической системой вычислений. Кроме того, впервые было реализовано автоматическое вычисление и проверка единиц измерения. На сегодняшний день MathCAD включает некоторые возможности алгебраических систем для ЭВМ, но при этом сохраняет ориентацию на инженерные приложения. Изначально MathCAD был создан Алэном Рэздоу из Массачусетского технологического института (MIT). Несмотря на то, что данная программа ориентирована на пользователей, мало знакомых с программированием, она всё же находит применение в достаточно сложных проектах для визуализации результатов математического моделирования с использованием распределённых вычислений и традиционных языков программирования. Рабочая область программы представляется как обыкновенный лист, на котором уравнения и выражения отображаются графически, а не в текстовом виде. Поэтому MathCAD может стать хорошим подспорьем для студентов и для преподавателей в освоении различных разделов курса «высшей математики», и в частности, линейной алгебры.
В настоящей работе предлагается MathCAD-документ некоторых лекций по курсу линейной алгебры. Рассмотрены операции над матрицами, реализованные с помощью встроенных функций MathCAD и по определению. Проверены численно свойства определителей. Приведены примеры нахождения обратной матрицы с помощью присоединённой, по алгоритму Гаусса-Жордана и с помощью оператора MathCAD. Выполнены LU-разложение, LDU-разложение, QR-разложение матриц. На наш взгляд такие лекции позволят:
- легче осваивать алгоритмы, так как уменьшается объем вычислительных работ, и вычисления не будут вызывать затруднения,
- рассматривать более сложные вопросы линейной алгебры, поскольку меньше времени уйдет на вычисления,
- некоторые результаты, которые лектор оставляет без доказательств, проверять численно,
- параллельно с лекциями можно осваивать MathCAD.
УДК 51-77
Балыкова К.А.
Группа 6172
Научный руководитель: Г.А. Петросян
ФЕНОМЕН РАЗВЛЕКАТЕЛЬНОСТИ.
Условия жизни в большом городе создают предпосылки для объединения молодежи в разнообразные группы, движения, являющиеся сплачивающим фактором, формирующие коллективное сознание в этих группах, коллективную ответственность и общие понятия о социально-культурных ценностях. Таким образом, появляются молодежные субкультуры. В социологии под субкультурой принято понимать систему ценностей и норм, установок, способов поведения, стилей определенной социальной группы, отличающихся от господствующей в обществе культуры, хотя и связанных с ней.
В психолого-педагогической литературе можно встретить следующую типологизацию молодежных субкультур: романтико-эскапистские субкультуры (хиппи, индеанисты, толкиенисты, с известными оговорками байкеры), гедонистическо-развлекательные (мажоры, рэйверы, реперы и т.п.), криминальные ("гопники", "люберы"), анархонигилистические (панки, экстремистские субкультуры "левого" и "правого" толка), которые можно также назвать радикально-деструктивными.
Основная черта развлекательной субкультуры - (рейверы, рокеры, мажоры) общие музыкальные вкусы, легкое беззаботное отношение к жизни, стремлению жить сегодняшним, «прикид» (особенности внешнего вида, одежды и движений). Представители этой субкультуры ценят саму возможность общения, «выплеска» радости, ухода в красивую действительность.
Создание математических моделей становится в социологии инновационным. Например, перенесем особенности развлекательной субкультуры в математическую модель, ограничиваясь стадией роста интереса к ней.
Пусть
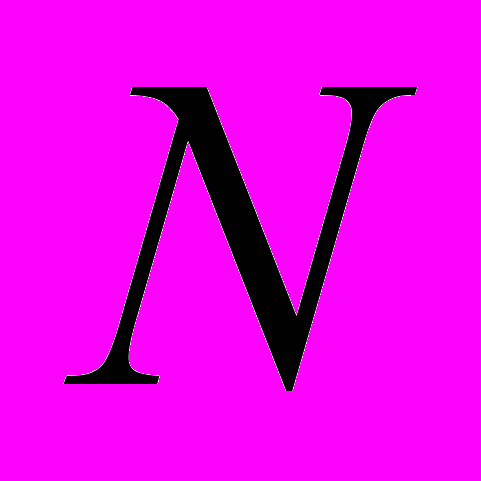– число представителей данной субкультуры, а 
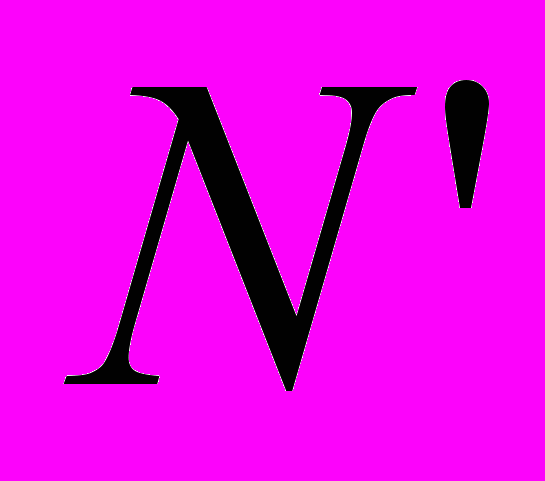- число склонных к ней, 
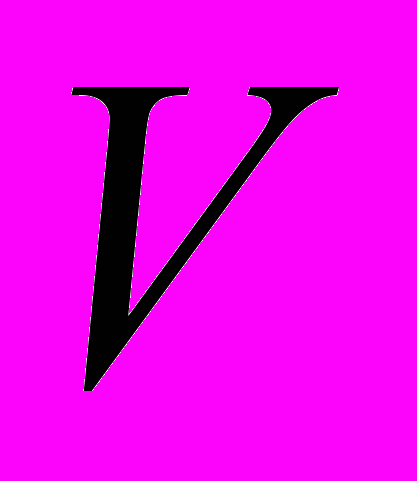– яркость этого образа жизни. Если притягательность к этому досугу создается не только личными наблюдениями, но и увлеченностью друзей, то пополнение группы увлеченных можно описать уравнениями
, 
, 
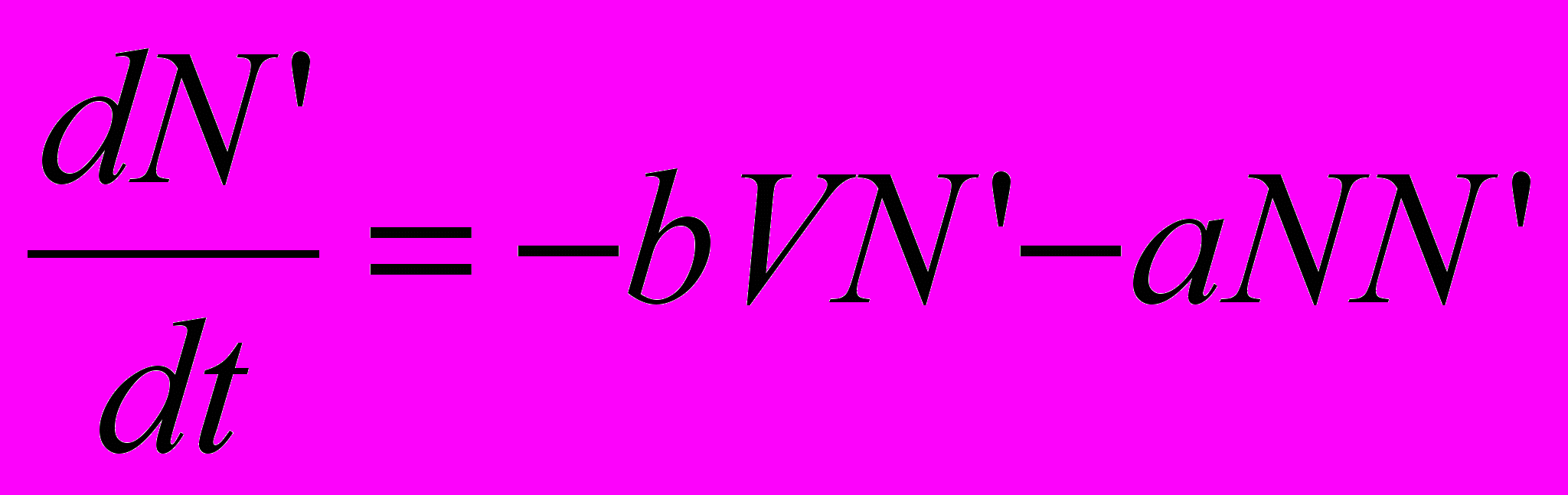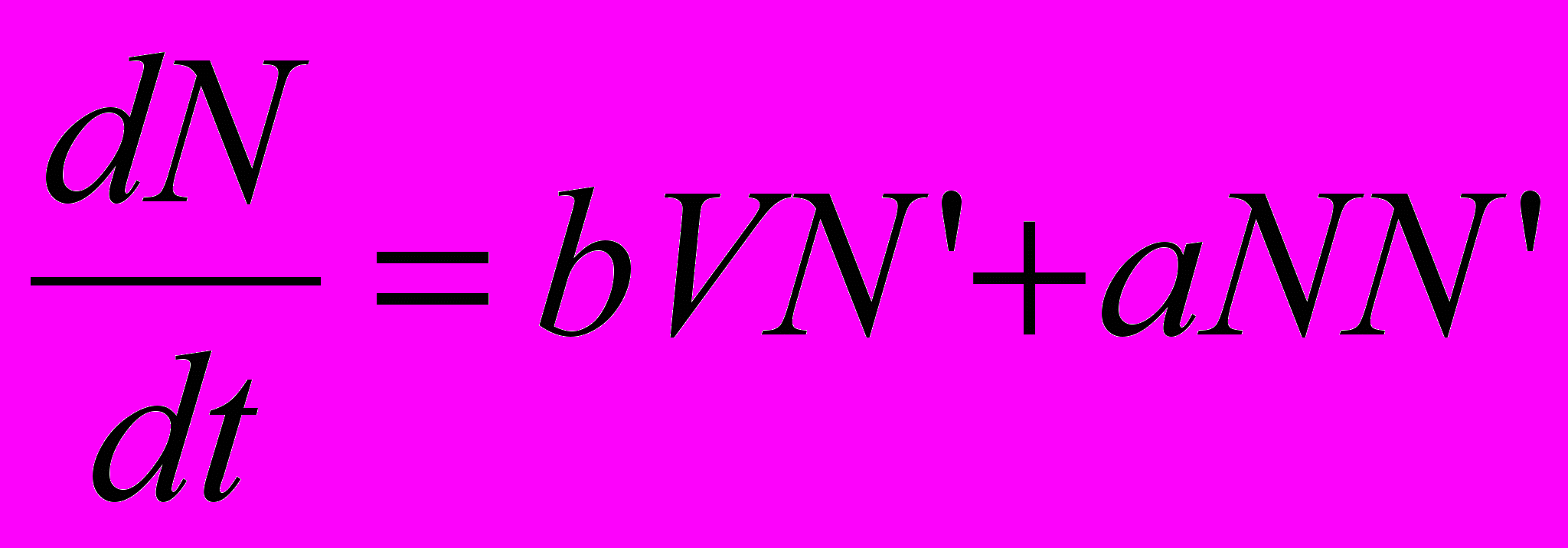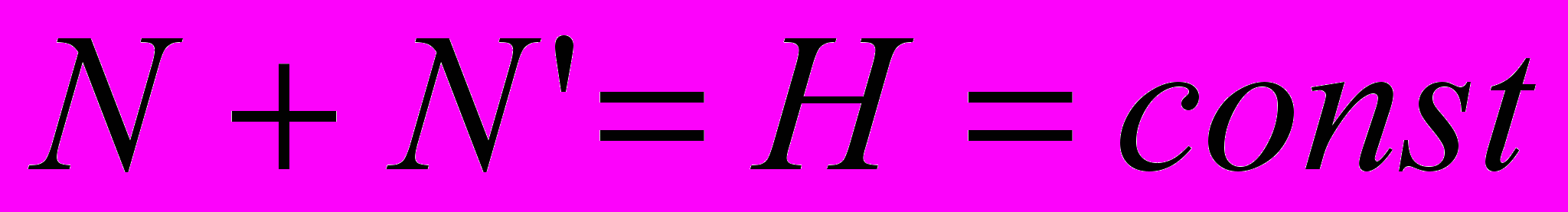
где компонента
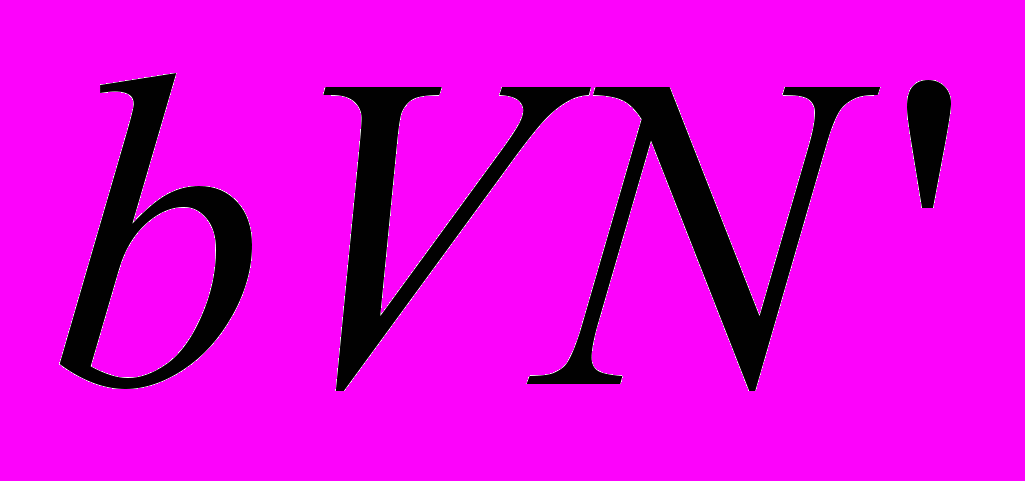описывает действие наблюдений, а компонента 
- действие друзей. В отношении яркости образа полагаем, что яркость получает приращение с ростом числа увлеченных, но падает в силу недолговечности полученных впечатлений (пусть - длительность сохранения живости впечатлений).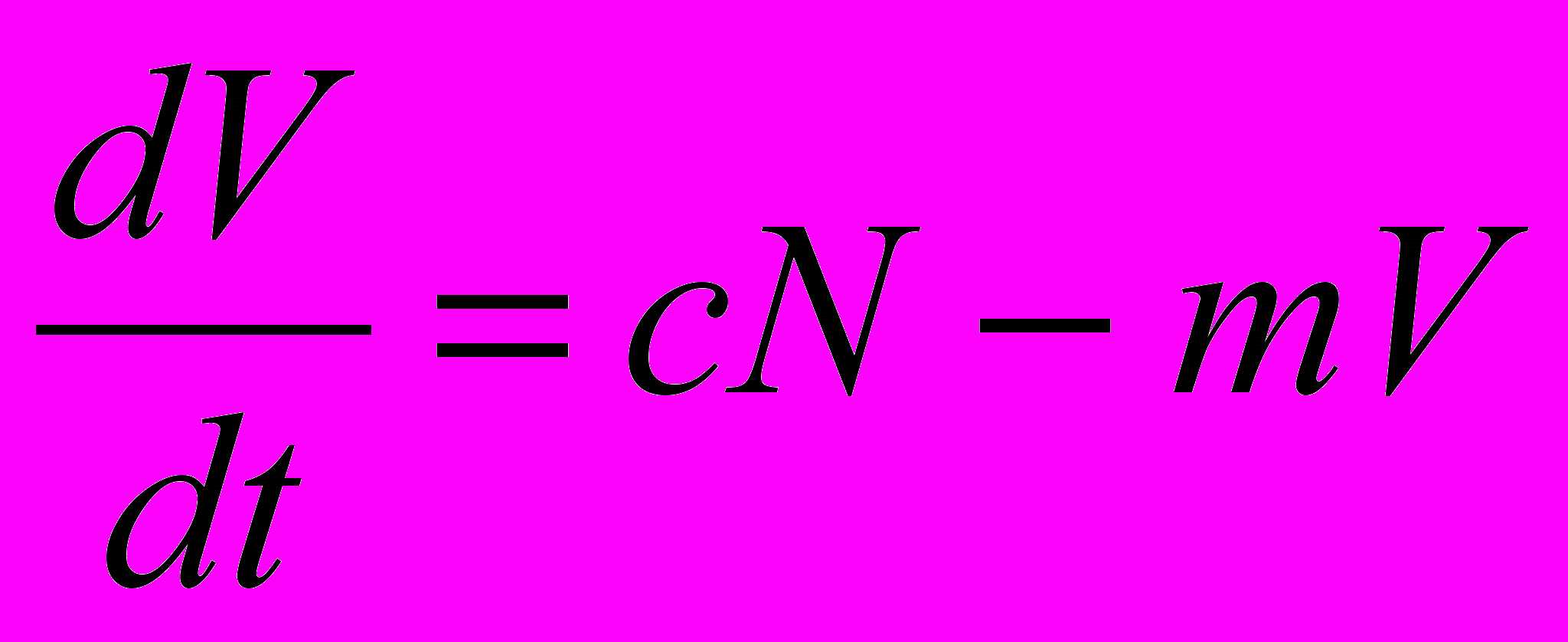
, 
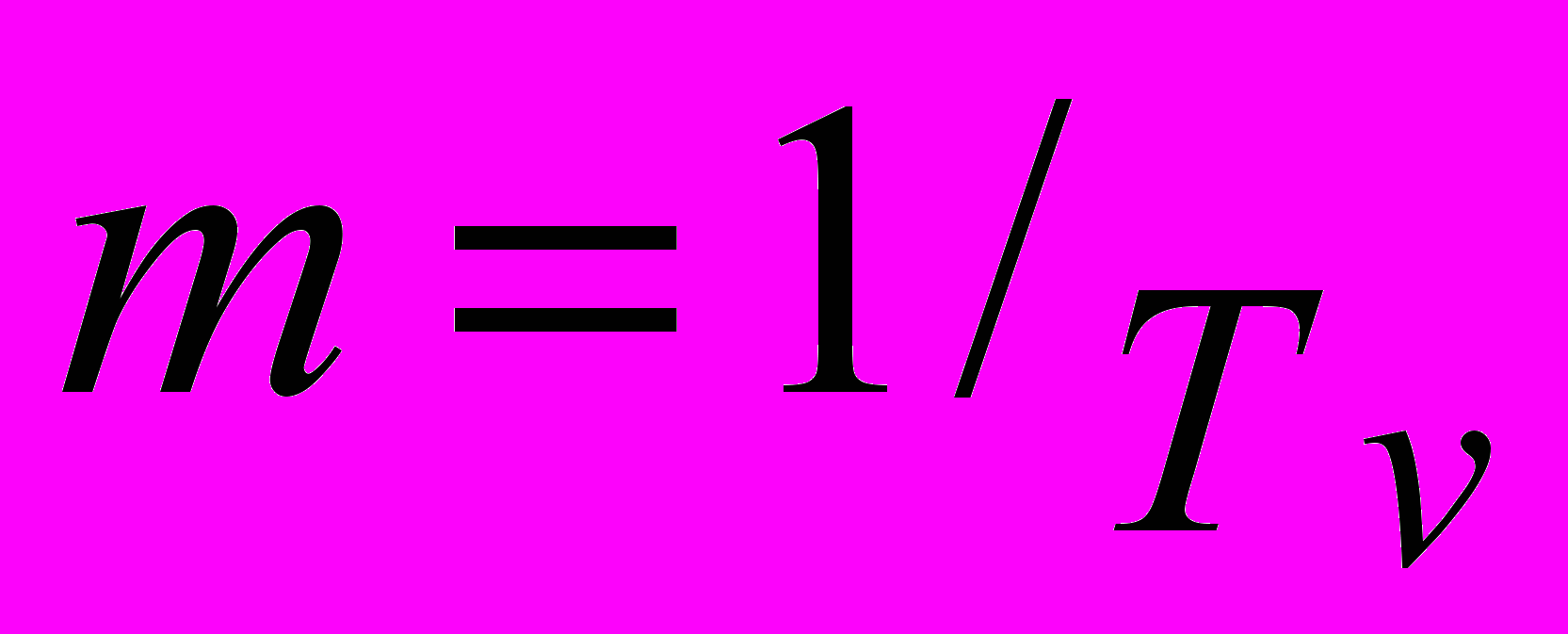
В итоге модель развития субкультуры получает вид
, 
, 
, 
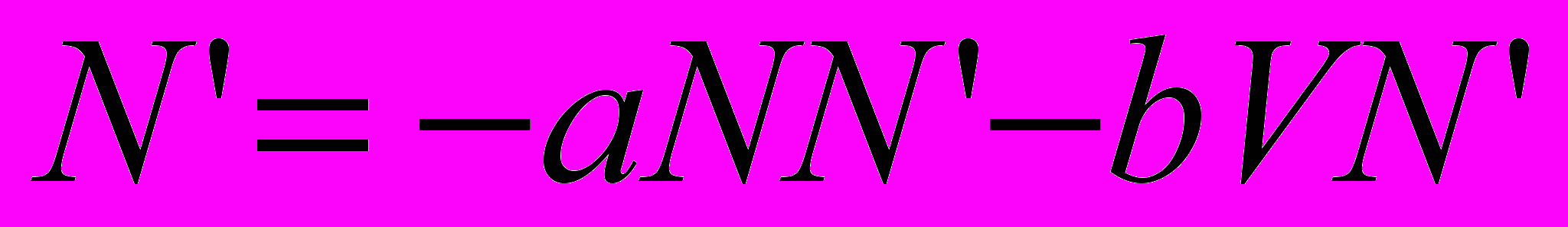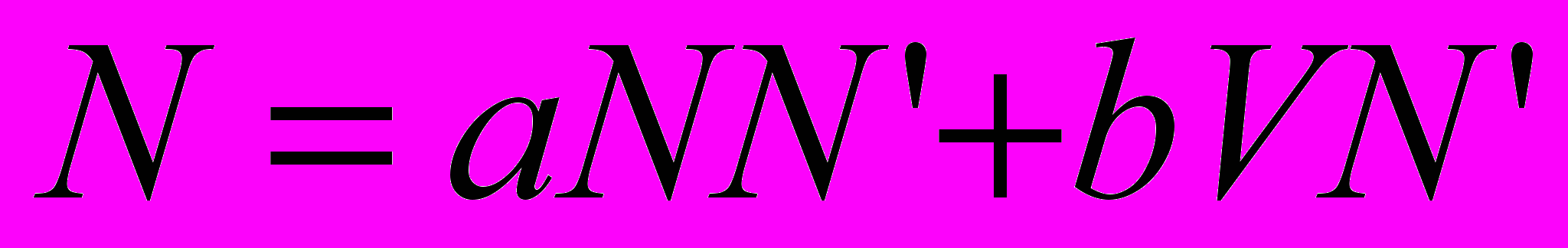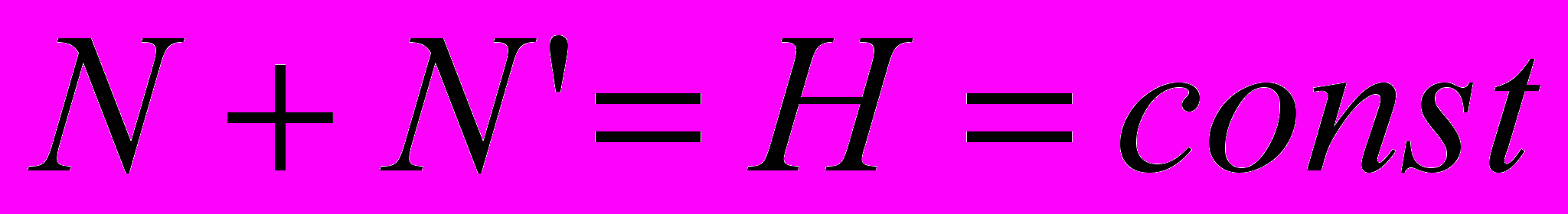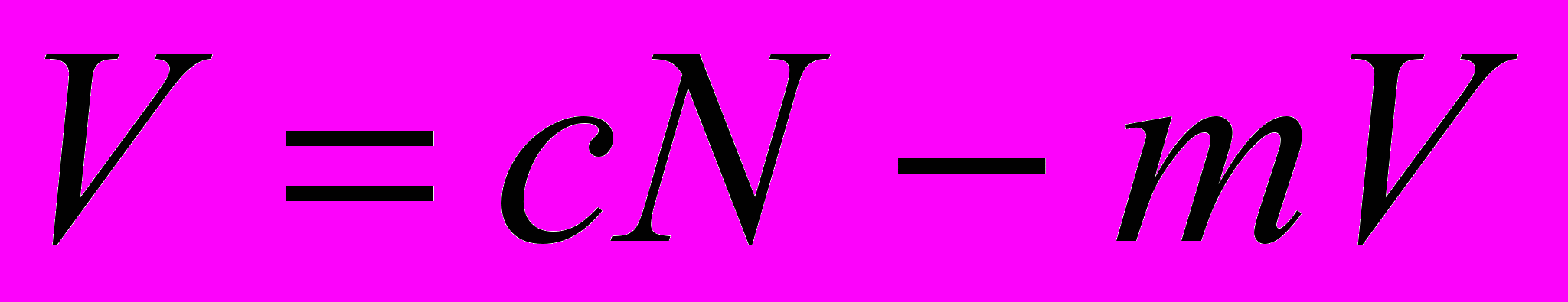.Эта модель может быть применена для расчета интереса молодежи и дальнейшего прогнозирования интереса к развлекательным субкультурам.
Выбирая определенную субкультуру, молодежь хочет объединяться, прежде всего, для занятий спортом, для содержательного и интересного проведения досуга, для занятий музыкой и искусством. На выбор определенного вида субкультуры влияет интересы, выбор друзей, яркость образа жизни.
УДК 59-77
Кузьмина М.В.
группа7282
Научный руководитель кандидат физико-математических наук доцент Гончар Лариса Исхаковна
МОДЕЛЬ ОПТИМИЗАЦИИ ОБЪЕМОВ ЗАКУПОК ТОРГОВО-КОММЕРЧЕСКОЙ ФИРМЫ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ
Метод ветвей и границ— общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации. По существу, метод является вариацией полного перебора с отсевом подмножеств допустимых решений, не содержащих оптимальных решений.
Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ). Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти. Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.
Общая идея метода может быть продемонстрирована на примере поиска максимума функции, которая описывает портфель закупок торгово-коммерческой фирмы с дальнейшей перепродажей для получения прибыли.
∑xiviβi+(F-∑xiviαi)→max
Где xi, i=1,2,…,s определены следующим образом: хi=1, если закупка vi включается в окончательный портфель и хi=0 в противном случае,
vi - объем покупки i-ого товара,
α - цена оптовой покупки i-ого товара (рублей за единицу),
β - цена розничной продажи этого товара,
F – объем свободных финансовых средств фирмы для первоначальной закупки товара.
Нужно максимизировать данную функцию при системе ограничений: денежные расходы на первоначальную закупку партий товаров не должны превзойти объема свободных денежных средств, находящихся в распоряжении фирмы. Также можно наложить временное ограничение, которое будет свидетельствовать о том, что закупать товара больше, чем его возможно продать на интервале времени [0; T] – нецелесообразно.