Внастоящее время в компьютерном мире существует множество языков программирования
| Вид материала | Документы |
- Календарный план учебных занятий по дисциплине «Языки и технология программирования», 43.35kb.
- Лекция №3. Состав и работа системы программирования Турбо Паскаль Язык программирования, 84.43kb.
- Лекция 3 Инструментальное по. Классификация языков программирования, 90.16kb.
- Внастоящее время существует большой социальный заказ на психологические методы профилактики, 117.85kb.
- Методические указания для выполнения лабораторных работ и курсовой работы содержание, 1317.09kb.
- Программа дисциплины Языки и технологии программирования Семестры, 20.19kb.
- Теория автоматов и формальных языков составил доцент А. А. Мальцев, 38.01kb.
- Внастоящее время в мире повсеместно и во все более разрастающихся масштабах происходит, 373.75kb.
- Вмире существует множество замечательных повестей, романов, рассказов и стихов, главными, 21kb.
- Пояснительная записка, 185.11kb.
2.4. Итоги
Во второй теме были изучены: типы переменных; операции над операндами; условные операторы.
При создании демонстрационной программы были получены навыки работы со следующими командами и визуальными компонентами: элементом фигура Shape; элементом изменения значения цифр SpinEdit; связыванием событий объектов.
3. Операторы цикла
Цель: Изучение стандартных функций; метки; изучение операторов цикла; отладка программ.
3.1. Теоретические сведения
Стандартные функции. Для выполнения часто встречающихся вычислений и преобразования данных в Object Pascal существуют стандартные функции.
Некоторые стандартные арифметические функции перечислены в таблице 3.1.
Таблица 3.1
| Функция | Действие |
| Abs(n) | Абсолютное значение значения n |
| Sqr(n) | Число n в степени 2 |
| Sqrt(n) | Корень квадратный из числа n |
| Sin(n) | Синус числа n |
| Cos(n) | Косинус числа n |
| ArcTan(n) | Арктангенс числа n |
| Exp(n) | Число е в степени n |
| Ln(n) | Натуральный логарифм числа n |
Для более сложных расчетов необходимо подключить к программе модуль Math. Для этого в разделе описания модулей (например, после слова implementation) добавить следующие строки: Uses Math;
Некоторые функции из этого модуля (арифметические, тригонометрические и для перевода углов из одной системы в другую) представлены в таблице 3.2.
Таблица 3.2
Функция | Действие | |
| Арифметические | ||
| Lnxp1(x) | Натуральный логарифм числа (x + 1) (использовать при х близких к 0) | |
| Ceil(x) | Ближайшее большее число к х | |
| Floor(x) | Ближайшее меньшее число к х | |
| Frexp(x,m,e) | Мантисса m и порядок e числа х | |
| IntPower(a,x) | а в целой степени х – ах | |
| LdExp(x,p) | Число х, умноженное на 2 в целой степени р – х*2р | |
| Log10(x) | Десятичный логарифм числа х (Lg(x)) | |
| Log2(x) | Двоичный логарифм числа х (Lb(x)) | |
| LogN(n,x) | Логарифм по основанию n числа х (Lognх) | |
| Max(a,b) | Максимальное число из двух чисел а и b | |
| Min(a,b) | Минимальное число из двух чисел а и b | |
| Poly(x,C) | Степенной ряд с коэфф. С (массив) – с0 + с1х + с2х2+…+ сnxn | |
| Power(a,x) | Число а в степени х (ах) | |
Таблица 3.2 (Продолжение)
Тригонометрические | ||
PI | Число ( ≈3,1415926535897932385) | |
| ArcCos(x) | Арккосинус х | |
| ArcCosH(x) | Гиперболический арккосинус х | |
| ArcSin(x) | Арксинус х | |
| ArcSinH(x) | Гиперболический арксинус х | |
| ArcTanH(x) | Гиперболический арктангенс х | |
| CosH(x) | Гиперболический косинус х | |
| Cotan(x) | Котангенс х (Cos(x) / Sin(x)) | |
| Hypon(a,b) | Гипотенуза прямоугольного треугольника -  | |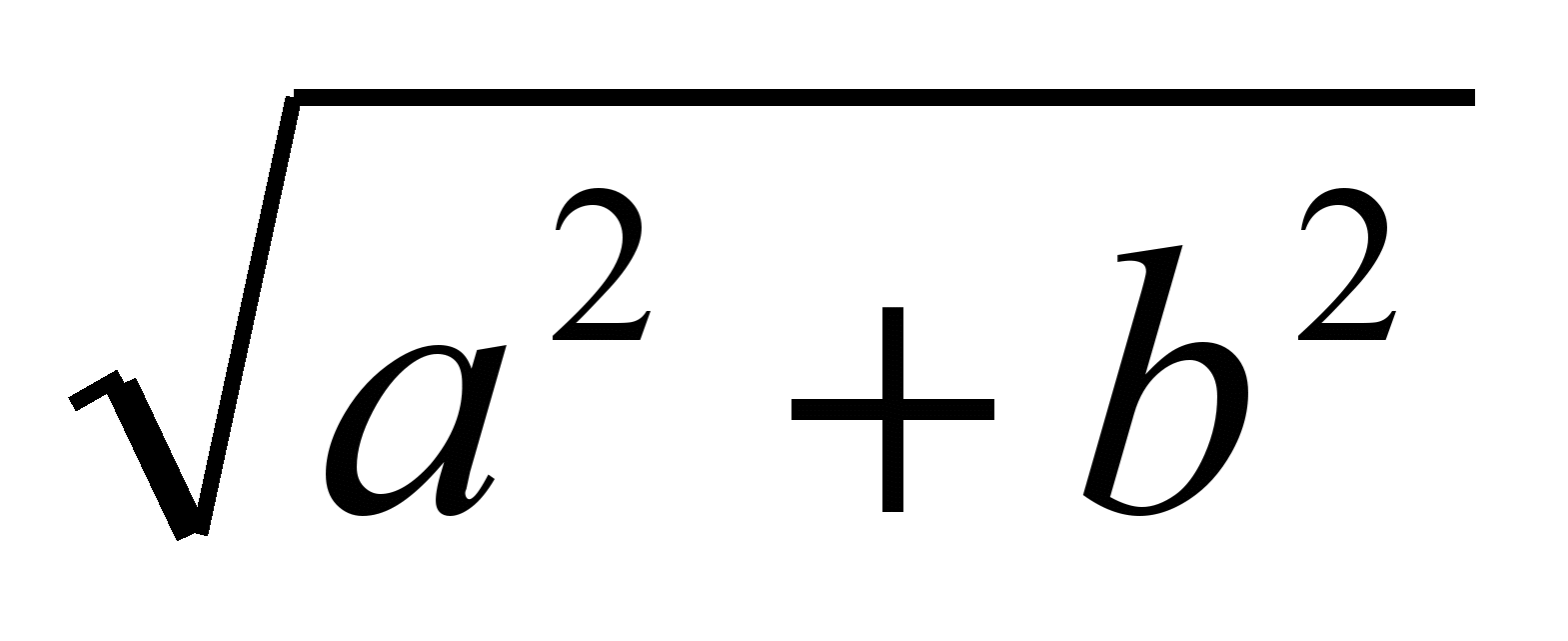
| SinCos(r,s,c) | Синус s и косинус с угла r в радианах | |
| SinH(x) | Гиперболический синус х | |
| Tan(x) | Тангенс х (Sin(x) / Cos(x)) | |
| TanH(x) | Гиперболический тангенс х | |
Перевод углов из одной системы в другую | ||
| CycleToRad(x) | Перевод периодов х в радианы (1 период соответствует 2) | |
| DegToRad(x) | Перевод градусов х в радианы (180 соответствует ) | |
| RadToCycle(x) | Перевод величины x, представленной в радианах, в периоды (2 соответствует период) | |
| RadToDeg(x) | Перевод величины х, представленной в радианах в градусы ( радиан соответствует 180) | |
Статистические расчеты | ||
| RandG(m,sd) | Генерация случайного числа по распределению Гаусса, задается m – математическое ожидание, sd-стандартное отклонение | |
| MaxIntValue(D) | Максимальное число из массива целых чисел D | |
| MaxValue(D) | Максимальное число из массива чисел D | |
| Mean(D) | Среднее число массива D | |
| MeanAndStdDev(D, m,sd) | Среднее число m и квадратичное отклонение sd массива D | |
| MinIntValue(D) | Минимальное число массива целых чисел D | |
| MinValue(D) | Минимальное число массива чисел D | |
| StdDev(D) | Квадратичное отклонение массива D  | |
| Sum(D) | Сумма всех чисел массива D | |
| SumInt(D) | Сумма всех целых чисел массива D | |
Функции преобразования типов. Функции преобразования служат для преобразования переменной одного типа к другому типу. Наиболее часто такие функции используются при вводе и выводе информации. Пример, для вывода значения переменной числового типа в поле ввода необходимо преобразовать значение в строковый тип, так как поле ввода позволяет выводить только строки. В таблице 3.3 перечислены основные функции преобразования типов.
Таблица 3.3
Функция | Значение |
| Chr(n) | Символ в стандарте ANSI с номером n |
Таблица 3.3 (Продолжение)
| IntToStr(n) | Преобразование целого числа n в строку |
| FloatToStr(n) | Преобразование вещественного числа n в строку |
| FloatToStrF(n,f,l,m) | Преобразование вещественного числа n в строку с форматом f, длинной строки l и количеством m цифр после десятичной точки |
| StrToInt(s) | Преобразование строки s в целое число |
| StrToFloat(s) | Преобразование строки s в вещественное число |
| Round(n) | Ближайшее к n целое |
| Trunc(n) | Целая часть от n |
| Frac(n) | Дробная часть вещественного числа n |
| Int(n) | Целая часть вещественного числа n |
Операторы цикла. При разработке алгоритмов решения большинства задач возникает необходимость повторения ряда шагов. Для организации новых повторов (циклов) можно использовать три разновидности операторов цикла: с параметром, с предусловием, с постусловием. Каждую разновидность цикла можно реализовать с помощью условного оператора и безусловного перехода (см. ниже).
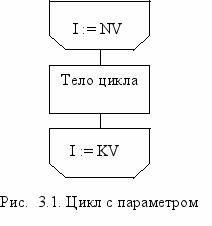
Если число повторений тела цикла заранее известно, то применяется оператор цикла с параметром. Структурная схема представлена на рис.3.1. Общий вид следующий:
For переменная := нач_значение to кон_значение do тело или
For переменная := нач_значение downto кон_значение do тело
где
п
еременная – параметр цикла, в качестве параметра может быть использована любая переменная перечисляемого типа (например, integer);нач_значение и
кон_значение – выражения, задающие начальное и конечное значение параметра цикла соответственно;
тело – простой или составной оператор.
Тип начального и конечного значений цикла должны совпадать с типом параметра цикла. Выполнение оператора цикла начинается с проверки условия переменная <= конзн для цикла to и переменная >= конзн для цикла downto. Если оно не выполняется, то оператор тело не выполняется и управление передается следующему за циклом оператору. Если же условие истинно, то выполняется оператор тело, затем параметру цикла переменная присваивается следующее значение (цикл to) или предыдущее значение (цикл downto). Далее процесс повторяется. Если параметр цикла целого типа, то это означает его увеличение (соответственно уменьшение) на единицу при каждом вычислении расположенного в цикле оператора.
Замечание: шаг изменения параметра всегда равен или 1 или –1.
Примеры:
(считается, что раздел переменных имеет следующий вид: var S,I: Integer; Sim : Char; L : Boolean;)
- S:= 0; For I := 5 to 7 do Inc(S);
Операция Inc(S,K) означает S := S + K, то есть увеличение параметра S на значение K. Если К не задан, то считается, что К = 1. (Обратная функция Dec(S,K) – уменьшение переменной S на значение К). В примере после выполнения цикла переменная S получит значение 3.
- S:=10; For I:= 10 downto 6 do Dec(S,2); S получит значение 0.
- S:=0; For Sim := ‘A’ to ‘D’ do S:= S + 1; S получит значение 4.
- S:=0; For L:=false to true do Inc(S,3); S получит значение 6.
Если в цикле необходимо выполнить несколько операторов, то используется составной оператор.
Пример:
S:=0;
For I:= 1 to 3 do
begin
S:= S + Sqr(I);
P := S + 1;
end;
После выполнения цикла переменная S станет равной 14, а переменная P равной 15.
Замечания:
- значение параметра цикла, начального и конечного значений параметра цикла изменять внутри цикла нельзя:
- Для принудительного выхода из цикла в Object Pascal используют команду Break;
- Для выполнения тела цикла сначала со следующим значением параметра цикла в Object Pascal используют команду Continue;
- При выходе из цикла значение параметра цикла не определено;
Оператор цикла с параметром позволяет осуществить цикл, когда известно сколько раз цикл должен быть выполнен, шаг цикла равняется 1 или –1. Но часто заранее неизвестно сколько раз должен быть выполнено тело цикла. Тогда необходимо использовать два других типа цикла: с предусловием или постусловием.
Оператор цикла с предусловием имеет вид:
while условие do тело;
где
условие – выражение условного типа;
тело - простой или составной оператор.
Структурная схема цикла показана на рис.3.2.
В
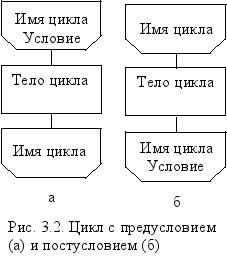ыполнение оператора начинается с вычисления значения выражения условие. Если это значение True, то выполняется оператор тело. Затем выполнение оператора цикла повторяется до тех пор, пока значение выражение условие не станет равным False. В этом случае управление передается оператору, стоящему за оператором цикла. Если значение выражения условие при первом входе в цикл равно false, то цикл не выполняется не разу. Замечание: один из операторов внутри цикла должен влиять на значение условие, иначе цикл будет повторяться бесконечно – происходит «зацикливание» программы. Пример:
k := 0;
while k <6 do
begin
Inc(k,2);
Y := Sqr(k);
end;
В примере использована процедура Inc(k,2), которая увеличивает значение переменной k на 2. Общий вид процедуры: Inc(перем [, знач]) – увеличить значение переменной перем на величину знач. При отсутствии величины знач переменная перем будет увеличина на 1. Процедура Dec(перем [, знач]) – уменьшает значение переменной перем на величину знач.
В процессе выполнения цикла переменная Y будет иметь значения 4, 16, 36.
Оператор цикла с постусловием имеет структурную схему, показанную на рисунке 3 и похож на оператор цикла с предусловием, но условие проверяется после выполнения операторов, составляющих тело цикла. Общий вид оператора:
Repeat
тело;
until условие;
где
условие - выражение логического типа;
тело - оператор или составной оператор;
Замечания:
- так как тело цикла заключено между ключевыми словами цикла, то при использовании в теле цикла составного оператора помещать его между операторными скобками begin и end не нужно;
- так как условие проверяется в конце цикла, то необходимо, чтобы цикл выполнялся как минимум один раз.
Оператор цикла с постусловием начинается с выполнения операторов внутри цикла. Затем вычисляется выражение условие. Если значение равно true, то осуществляется выход из цикла, а при значении false выполнение тела повторяется.
Замечание: выход из цикла с предусловием осуществляется при достижении ложности условия, а цикла с постусловием при достижении истинности условия.
Пример: возьмем тот же пример, что и в цикле с предусловием:
k:=0;
repeat
Inc(k,2);
Y := Sqr(k);
until(k>6);
результат будет тот же.
Любой тип оператора цикла может быть построен с помощью условного оператора. Например, структурная схема цикла с постусловием, построенным, с помощью условного оператора, показана на рис 3.3.
П
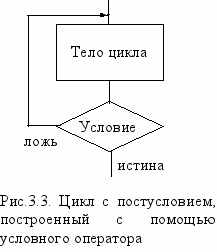ри построении такого цикла необходимо переслать информационный поток перед операторами цикла. Для таких целей необходимо использовать метки и оператор безусловного перехода – goto. Как и переменные метки должны быть объявлены. Метки объявляются в разделе меток (Label). При использовании метки необходимо использовать имя метки и двоеточие. Переход на метку осуществляется командой goto метки. Рассмотрим тот же пример, но с использование условного оператора. В разделе меток необходимо описать метку. Пусть имя метки beg.
Пример:
Label
beg;
begin
{прочие операторы}
k:=0;
beg :Inc(k,2);
Y := Sqr(k);
If k < 6 then goto beg;
{прочие операторы}
end;
Рекомендация: Использование безусловного оператора goto затрудняет «легкость» чтения текста программы программистом, поэтому использовать безусловный переход не рекомендуется.
Отладка программы. При построении сложных программ могут возникать ошибки. Ошибки принято делить на три группы:
- Синтаксические;
- Ошибки времени выполнения;
- Алгоритмические.
Наиболее простые из них синтаксические – ошибки набора текста – они исправляются в процессе компиляции программы. Ошибки времени выполнения – ошибки, возникающие при несоответствии типов введенных параметров типам используемых переменных или ошибки вычислений (например, деление на 0), отслеживаются также не сложно уже при первых запусках программы. Будем считать, что программа запускается из оболочки Delphi. После возникновения такой ошибки необходимо нажать «Ok» в окне сообщения об ошибке, а затем завершить выполнение программы – пункт меню «Run/Program reset» или нажать комбинацию клавиш <Ctrl><F2>. При возникновении такой ошибки курсор в программе будет указывать на строку вызвавшую ошибку. Наиболее сложно находимые являются алгоритмические ошибки. Программа компилируется без ошибок, не дает ошибок при пробных запусках, но при анализе результатов выясняется, что результат неправильный. Необходимо вручную «прокрутить» алгоритм – требуется отладка программы.
Для трассировки программы (проверка «логики алгоритма»), то есть выполнения программы по шагам, необходимо выполнить следующие действия. В пункте меню выбрать пункт «Run/Step over» или «Run/Trace in to», им соответствуют клавиши <F8> и <F7> соответственно, команда «Run/Trace in to» отличаются более детальной трассировкой. Для прекращения трассировки и продолжения выполнения программы в автоматическом режиме необходимо выбрать пункт «Run/Run» или нажать <F9>. Остановить программу можно с помощью команды «Run/Program reset» или нажать комбинацию клавиш <Ctrl><F2>. Иногда необходимо выполнить трассировку с определенной строки программы. Для этой цели подводят курсор к интересующей строке и выполняют команду «Run/Run to cursor» или нажимают <F4>. Часто известно, где может быть ошибка алгоритма – тогда используют точку останова. Программист устанавливает на нужной строке курсор и ставит там точку останова с помощью команды «Run/Add Breakpoint» или, нажав <Ctrl><F8>. Выбранная строка будет отмечена. Для снятия точки останова необходимо на этой строке снова нажать <Ctrl><F8>. При выполнении программы, программа будет выполняться до точки останова, затем программист сможет трассировать программу с помощью <F7> и <F8>. При необходимости можно указать условие, по которому будет происходить остановка на точке останова (эта настройка осуществляется в окне «Breakpoints», пункт меню «Run/Add breakpoints»).
При выполнении программы по шагам часто необходимо проверять не только правильность «логики алгоритма», но знать и значения некоторых переменных. Для этой цели выполняют команду «View/Watch/Add watch» и вводят имя интересующей переменной. Эту команду можно выполнить и так – подвести курсор к переменной, значение которой необходимо просмотреть и нажать <Ctrl><F7>. При трассировке программы в этом случае в окне «Watch list» можно видеть изменение значения интересующих переменных.