1. Кодирование информации

Вид материала

Содержание

Бинарное множество
1.2.Системы счисления
1.3.Кодирование чисел в компьютере
1.4.Кодирование букв алфавита
1.5.Кодирование произвольной информации
Двоичные коды
1.6.Коды постоянной длины
Расстояние Хэмминга
1.7.Коды переменной длины
1.8.Префиксные коды
1.9.Теорема кодирования
Количество информации
Средняя длина кодовых слов
Эффективность кода
1.10.Надежность кодов.

Подобный материал:

1.Кодирование информации

1.1.Общие определения

Кодировка – система, позволяющая осуществлять переход от одной знаковой системы представления информации к другому представлению той же информации также в виде знаков и их последовательностей.

Знак – элемент конечного множества, обладающий информационным содержанием, отличающийся от других знаков данного множества.

Запас знаков – конечное множество А знаков.

Алфавит – конечное и линейно упорядоченное множество символов.

Пример алфавита – 12 знаков зодиака, алфавит греческих букв и т.д.

Множество А может включать подмножества, которые могут образовывать запасы знаков меньших алфавитов.

Бинарное множество В={0,1} содержит всего два знака.

Слово – конечная последовательность знаков. Длина слова связана с размером алфавита.

Множество слов над А – множество конечных последовательностей знаков А* над запасом знаков А.

Множество слов В*={0,1}* называется множеством двоичных слов. Элементы этого множества называются n-битовыми словами или двоичными словами длины n.

1.2.Системы счисления

Числовая информация может быть представлена в одной из известных систем счисления. Наибольшее распространение получили позиционные системы счисления.

Числа в позиционной системе счисления с основанием В записываются при помощи цифр а_i, входящих в алфавит {a₁, a₂, a₃, … , a_i}, содержащий ровно В элементов.

Представление числа в позиционной системе счисления с основанием В имеет вид:

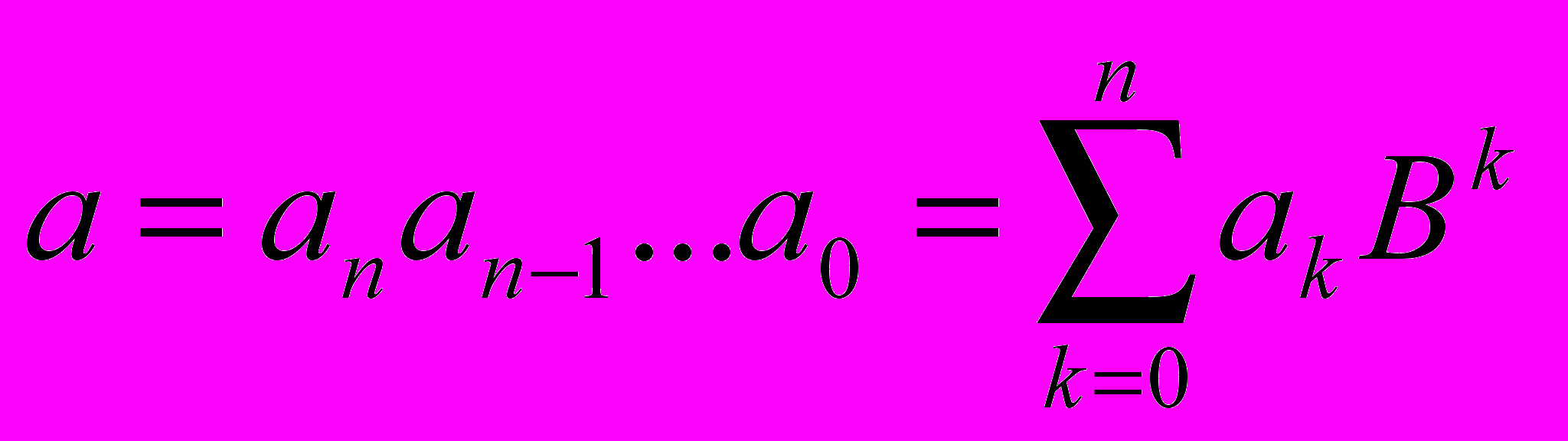[1]

Пример 1. 123₁₀=1*10²+2*10¹+3*10⁰ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Пример 2. 123₁₆=1*16²+2*16¹+3*16⁰=256+32+3=291₁₀ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

Пример 3. 10110₂=1*2⁴+1*2²+1*2¹=16+4+2=22₁₀ {0, 1}

В то же время известны и другие способы кодирования чисел. Так, например, с помощью римских цифр можно записать целые положительные числа, но эта система счисления не является позиционной, так как любой знак имеет строго определенное числовое значение.

Пример 4. I=1 V=5 X=10 L=50 C=100 M=1000 MCLXVI=1166₁₀

1.3.Кодирование чисел в компьютере

Компьютеры оперируют с числами, представленными в двоичной системе счисления. Это связано прежде всего с технической простотой хранения и преобразования двоичных чисел. При операциях с числами в компьютере число двоичных разрядов для представления чисел обычно фиксировано. Отдельный двоичный разряд называется бит, так что можно говорить о числах, имеющих 8 битов, 16 битов и т.д. Количество неотрицательных чисел, представимых с помощью n битов, очевидно равно 2ⁿ-1. Для представления отрицательных чисел диапазон представляемых положительных чисел ограничивают, а освобождающиеся при этом кодовые комбинации интерпретируют как отрицательные числа. При использовании дополнительного кода отрицательное число –х кодируется числом 2ⁿ–x, а диапазон представимых чисел несимметричен относительно нуля –2^n–1 x  2^n–1–1. Старший бит a_t представляет знак числа:

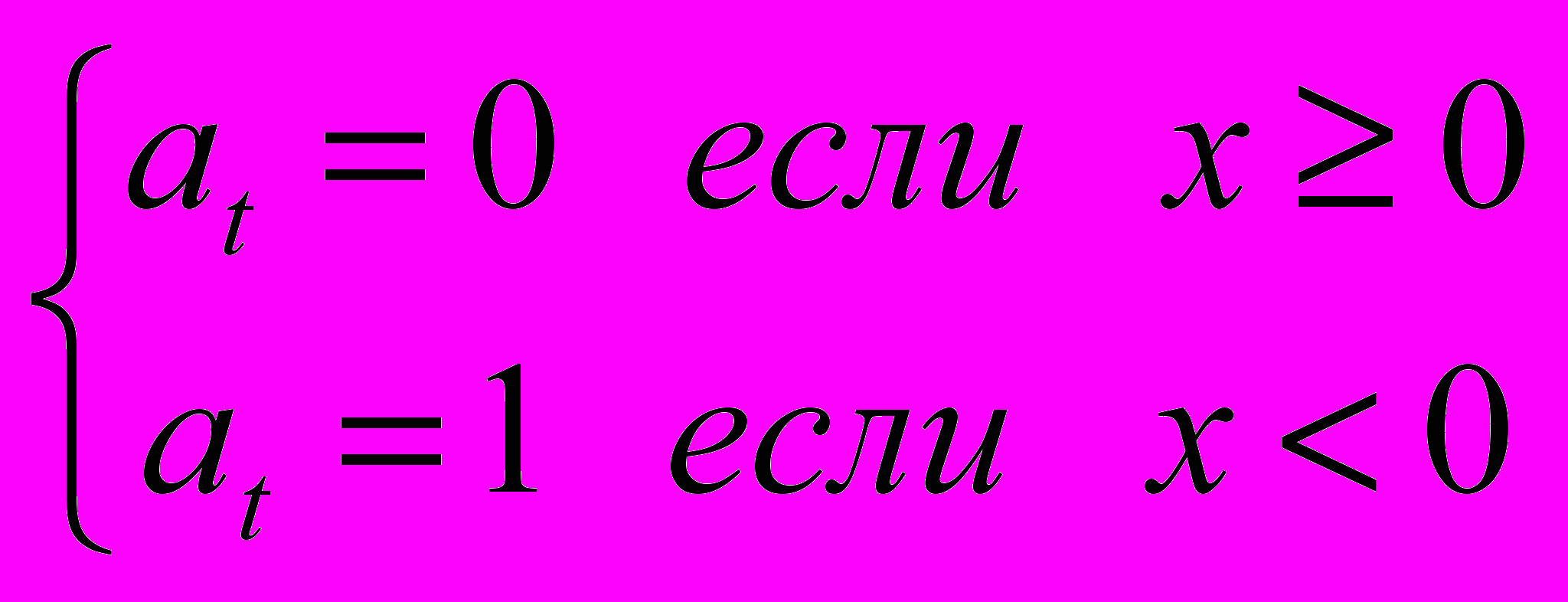[2]

Числа в двоичной системе счисления можно трактовать, в более общем смысле, как слова, записанные в алфавите {0,1}. В виде двоичных слов можно представлять не только числа, но и любые другие элементы произвольных конечных множеств.

1.4.Кодирование букв алфавита

Для изображения информации часто используются тексты на том или ином языке. Множество букв алфавита языка конечно и может быть записано в виде двоичных кодов. Существует стандартная кодировка букв английского алфавита ASCII (American Standard Code for Information Interchange - Американский стандартный код для обмена информацией). Это семибитный код, в котором кроме букв английского алфавита (строчных и прописных) представлены также цифры, знаки препинания, некоторые дополнительные знаки и управляющие коды (например, перевод строки). Для представления букв других алфавитов (кроме английского) используется расширение кода ASCII до 8-битового (extended ASCII); при этом литеры дополнительного алфавита кодируются двоичными числами, старший бит которых равен 1, тогда как для исходных кодов ASCII он равен 0.

1.5.Кодирование произвольной информации

Обратимся теперь к вопросам двоичного кодирования последовательностей произвольных символов. Для простоты мы будем использовать термин «текст» для обозначения любой последовательности символов независимо от их характера и назначения. Сюда войдут, например, тексты программ, цифровые представления изображений, музыки, видеофильмов, компьютерных игр и т.д. Кодирование устанавливает взаимно однозначное соответствие между исходными символами и/или их различными комбинациями, с одной стороны, и отдельными двоичными символами и/или их различными комбинациями - с другой.

Кодирование – отображение, переводящее множество символов (запас знаков) A в множество символов (запас знаков) B:

cod: A  B [3]

В случае кодирования слов, а не знаков, можно записать:

cod: A*  B* [4]

В общем случае предполагается, что кодирование является обратимой операцией.

Декодирование – обратное отображение символов множества B в множество A:

decod: { cod(a): a  A }  A [5]

Двоичные коды – множество B^* двоичных слов над алфавитом B = {0, 1}.

В результате такого кодирования исходный текст преобразуется в последовательность двоичных символов, длина которой при заданном тексте в общем случае будет различной в зависимости от выбранного метода кодирования. Естественно, что при прочих равных условиях предпочтение следует отдавать тем методам кодирования, которые исходный текст преобразуют в последовательность двоичных символов меньшей длины. Тем самым достигается экономия памяти и времени передачи этих текстов по каналам связи.

1.6.Коды постоянной длины

Код постоянной длины – двоичное кодирование, отображающее каждый кодируемый знак на двоичное слово одинаковой длины.

cod: A  Bⁿ [6]

Пусть объектом кодирования являются тексты, записанные на некотором (естественном или искусственном) языке, причем число букв в алфавите этого языка, включая (если есть такая необходимость) некоторые знаки препинания, знак пробела и т.п., равно n.

Далее, пусть L – наименьшее натуральное число, удовлетворяющее условию:

L  log₂n [7]

Тогда можно пользоваться простейшим методом побуквенного кодирования с помощью кода постоянной длины L. Наиболее компактное кодирование достигается в том случае, когда число букв в алфавите равняется целой степени двойки. Нарушение этого условия непременно приводит к некоторой избыточности.

Например, рассмотрим кодирование букв русского алфавита. Для компактности кодирования исключим из исходного алфавита A букву «ё». В таком случае для кодирования оставшихся 32 букв будет достаточно кода длины L = log₂32 = 5.

А	00000	И	01000	Р	10000	Ш	11000
Б	00001	Й	01001	С	10001	Щ	11001
В	00010	К	01010	Т	10010	Ъ	11010
Г	00011	Л	01011	У	10011	Ы	11011
Д	00100	М	01100	Ф	10100	Ь	11100
Е	00101	Н	01101	Х	10101	Э	11101
Ж	00110	О	01110	Ц	10110	Ю	11110
З	00111	П	01111	Ч	10111	Я	11111

Возникает вопрос, имеются ли резервы для дальнейшего сокращения числа двоичных символов, отводимых под одну букву? Оказывается, что такие резервы есть. С учетом неравновероятности встречаемости различных букв представляется естественным отказаться от постоянства длины кодовых наборов и стараться осуществить такое кодирование, при котором наиболее часто встречающиеся буквы были бы закодированы возможно более короткими кодовыми словами и, наоборот, наибольшую длину имели бы кодовые слова, соответствующие наименее часто встречающимся буквам. В связи с переходом к переменной длине кодовых наборов возникает проблема установления границ между ними при декодировании.

Расстояние Хэмминга – количество позиций, в которых отличаются двоичные слова a и b одинаковой длины.

Код Грэя (одношаговый код) – код постоянной длины, в котором коды двух последовательных знаков из линейно упорядоченного алфавита А различаются точно в одном бите.

Расстояние отображения кодировки для длины кодов n определяется через минимальное расстояние Хэмминга между двумя различными кодами. Большее расстояние кода допускает распознавание (или даже исправление) ошибок за счет избыточности кода. Они более надежны, но требуют дополнительных затрат на представление.

1.7.Коды переменной длины

Код переменной длины – более экономны, но труднее в обработке.

Код Морзе строится из трех знаков – (.) точка (короткая передача), (–) тире (длинная передача, (_) пробел (пауза).

В двоичном кодировании

C:{., –, _} –> {01, 0111, 000}

c(.)=01, c(–)=0111, c(_)=000.

Код телефонных систем для импульсного набора цифр

1	2	3	4	5	6	7	8	9	0
10	110	1110	11110	111110	1111110	11111110	111111110	1111111110	11111111110

1.8.Префиксные коды

Код называется префиксным, если кодовое слово ни одного знака не является началом (префиксом) кодового слова другого знака (условие Фано). Слова префиксного кода можно записывать в одну цепочку, не используя разделительных символов (запятых). Любую такую цепочку можно единственным образом разделить на ее компоненты. Префиксный код называется полным, если добавление к нему любого нового кодового слова нарушает свойство префиксности.

Пусть, например, буквам A, B и C поставлены в соответствие кодовые слова 00, 01 и 1. Рассмотрим произвольную последовательность нулей и единиц. Ее можно разделить на кодовые слова единственным образом, а именно: 00101011001101  00 1 01 01 1 00 1 1 01

Естественно, что полные коды представляют наибольший интерес, так как при прочих равных условиях они более компактны, чем неполные.

1.9.Теорема кодирования

Стохастический источник сообщений генерирует тексты в виде последовательности символов с заданным алфавитом и стационарными (не зависящими от времени) статистическими характеристиками появления элементов алфавита в последовательности. В простейшем случае каждый символ a_iA появляется независимо от других с вероятностью p(i).

Количество информации, приносимое в среднем одним элементом сообщения (текста), по определению равно энтропии источника:

H = –

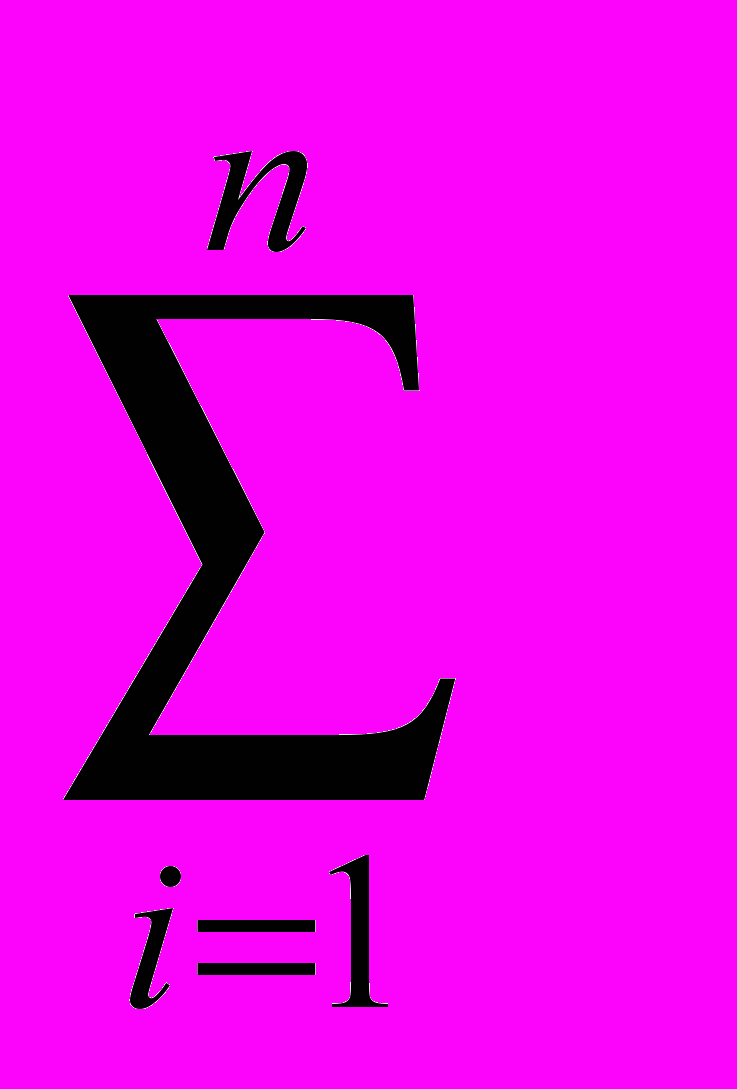p(i) log₂p(i) [8]

Энтропия источника H является непрерывной функцией от p(i). При фиксированном n энтропия максимальна и равна log₂n в случае, если все p(i) равны между собой. Обозначим длину i-го кодового слова как |cod(a_i)|.

Средняя длина кодовых слов может быть определена следующим образом:

L =  p(i) |cod(a_i)| [9]

Теорема кодирования: Для любого двоичного кодирования LH. Каждый источник может быть закодирован так, что разность L–H будет сколь угодно малой.

Эффективность кода: отношение H/L [10]

Избыточность кода: отношение (L–H)/L [11]

Общее правило построения наиболее эффективного кода неизвестно. Однако, предложен ряд алгоритмов, приводящих к построению двоичных кодов с эффективностью, близкой к максимальной. Для повышения эффективности двоичного кода необходимо соблюдение следующих условий:

1. вероятности появления двоичных символов «0» и «1» должна быть равны;

2. вероятности появления «0» и «1» не должны зависеть от того, какие символы им предшествовали.

1.10.Надежность кодов.

При передаче сообщений важно обнаружить ошибки и, по возможности, исправить их. Для увеличения надежности передачи используется избыточное кодирование, т.е. увеличение расстояния Хэмминга.

Лемма (обнаружение ошибок). Если код имеет расстояние Хэмминга h, то все ошибки, которые встречаются менее чем в h битах, могут быть обнаружены.

Как следствие, все ошибки, появляющиеся менее, чем в h/2 битах, могут быть исправлены, если для коррекции используется кодовое слово с расстоянием h. Таким образом. при h=2 можно обнаружить ошибочный бит, а при h=3 один бит можно исправить, а два обнаружить.

Код флексорайта. К каждому слову добавляется контрольный бит таким образом, чтобы общее число единичных битов в коде было четным. Если при передаче испорчен только один бит, то контрольный бит для возникшего слова некорректен, что обнаруживает ошибку.

Blog