Зміст вступ 5
| Вид материала | Документы |
Содержание§ 3.2 Стандартні математичні функції |
- Зміст, 429.02kb.
- Зміст, 329.83kb.
- Зміст вступ, 361.97kb.
- Зміст, 242.29kb.
- Зміст, 384.58kb.
- Зміст, 410.71kb.
- Зміст вступ, 388.95kb.
- Зміст перелік скорочень, 569.12kb.
- Зміст вступ, 540.64kb.
- Зміст Вступ, 574.44kb.
§ 3.2 Стандартні математичні функції
Крім шести арифметичних операцій, у мові Pascal є ще ряд математичних функцій, з деякими з яких ви вже встигли познайомитись на уроках математики, а деякі будете вивчати трохи пізніше. Опишемо всі математичні функції і приведемо приклади їх застосування.
Abs(x) – модуль числа х. На мові математики еквівалентне запису |х|. Як змінна х так і результат дії над нею функції Abs може набувати як цілочисельного типу, так і типу Real – дійсні числа.
Sqr(x) – квадрат числа х. На мові математики еквівалентне запису х2. Як змінна х так і результат дії над нею функції Sqr може набувати як цілочисельного типу, так і типу Real – дійсні числа.
Sqrt(x) – корінь квадратний з числа х. На мові математики еквівалентне запису
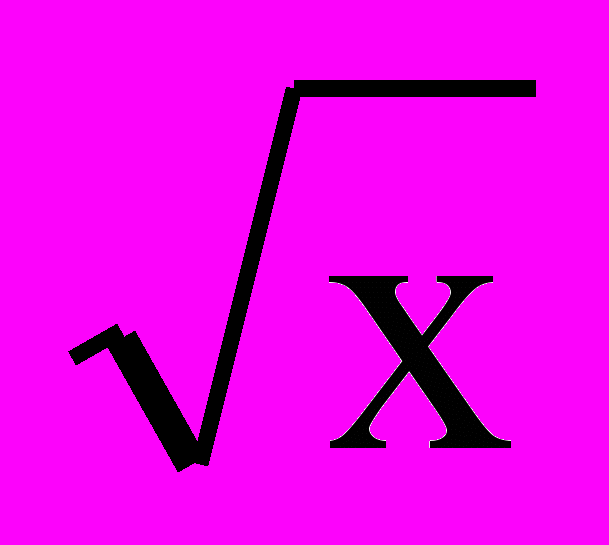 . Результат дії над змінною функції Sqrt набуває типу Real – дійсні числа.
. Результат дії над змінною функції Sqrt набуває типу Real – дійсні числа.Дві наступні функції знають старшокласники, для інших просто слід запам’ятати, що вони визначені в розглядуваній мові як математичні операції.
Exp(x) – експонента числа х. На мові математики еквівалентне запису ех. Результат дії над функції Exp набуває типу Real – дійсні числа.
Ln(x) – натуральний логарифм числа х. На мові математики еквівалентне запису ln х. Результат дії функції Ln набуває типу Real – дійсні числа.
Для розуміння наступних трьох функцій введемо нову міру для вимірювання кута.
Означення: Центральний кут, довжина дуги якого дорівнює радіусу кола називається кутом в 1 радіан.
Оскільки довжина кола L = 2pR, то коло містить 2p радіан, тобто 2p=360о. Знаючи це співвідношення легко переводити кути з радіанної міри в градусну і навпаки. Наш електронний партнер знає лише вимірювання кута в радіанах, тому всі наступні значення кута, де це не буде обумовлено нами окремо, вимірюються в радіанах. Саме тому значення числа p ПЕОМ в мові Pascal знає, але позначається дана константа як pi. У пам’яті комп’ютера зберігається число pi=3.1415926536, про що ми вже згадували раніше. Якщо вам необхідно використовувати градусну міру вимірювання кута, то необхідно самостійно виконати нескладні математичні перетворення, що базуються на властивостях пропорцій. Наголошуємо ще раз, що у всіх подальших записах кут буде виражено в радіанах.
Sin(x) – cинус кута х. На мові математики еквівалентне запису Sin х. Результат дії функції Sin набуває типу Real – дійсні числа.
Cos(x) – коcинус кута х. На мові математики еквівалентне запису Cosх. Результат дії функції Cos набуває типу Real – дійсні числа.
Arctan(x) – арктангенс числа х. На мові математики еквівалентне запису arctg х. Результат дії функції Arctan набуває типу Real –дійсні числа і міститься на проміжку від –p/2 до + p/2.
Крім цих тригонометричних функцій, в мові визначені ще і такі операції:
Round(x) – округлює число до цілого, згідно математичних правил округлення. Результат дії функції Round набуває типу Integer або Longint – цілі числа у вказаних для даного типу межах.
Trunc(x) – ціла частина числа: від числа відкидається дробова частина. Результат дії функції Trunc набуває типу Integer або Longint – цілі числа у вказаних для даного типу межах.
Frac(x) – дробова частина числа: відкидається ціла частина, а дробова частина записується як ціле число. Результат дії функції Frac набуває типу Integer або Longint – цілі числа у вказаних для даного типу межах.
Odd(x) – визначає, до парних чи непарних чисел відноситься дане число. Результат дії функції Odd набуває типу Boolean – true, якщо число парне або false в противному випадку.
Int(x) – ціла частина числа, тобто, те ж саме, що і функція trunc, але на відміну від дії функції trunc, результат дії функції Int залишається типу real.
Для прикладу розв’яжемо декілька задач.
Задача 11 Обчислити площу трикутника, якщо відомо координати його вершин.
Розв’язання : Досить відома в математиці задача, розв’язання якої базується на знанні формули Герона та знаходження довжини відрізка на підставі координат його кінців у декартовій системі координат. Для спрощення будемо вважати, що координати вершин трикутника завжди є цілими числами. Всі інші дії прокоментуємо в коментарях до програми.
program geron;
var xa, ya, xb, yb, xc, yc : integer;
a, b, c, S, p : real;
begin
write('Координата Х точки А: ');readln(xa);
write('Координата Y точки А: ');readln(ya);
write('Координата Х точки B: ');readln(xb);
write('Координата Y точки B: ');readln(yb);
write('Координата Х точки C: ');readln(xc);
write('Координата Y точки C: ');readln(yc);
a := sqrt(sqr(xc-xb)+sqr(yc-yb)); { Довжина сторони а }
b := sqrt(sqr(xc-xa)+sqr(yc-ya)); { Довжина сторони b }
c := sqrt(sqr(xb-xa)+sqr(yb-ya)); { Довжина сторони с }
p := (a + b + c)/2; { Пiвпериметр }
S := sqrt(p*(p-a)*(p-b)*(p-c)); { Формула Герона }
write(' S = ',S:4:2);
readln;
end.
При розв’язанні даної задачі можна було обійтись без введення додаткових змінних для обчислення довжин сторін і півпериметра, але в цьому випадку значно збільшився б вираз для обчислення площі і значення виразу для обчислення площі стало б практично не зрозумілим із–за його складності.
Введення додаткових змінних полегшує написання зрозумілих програм, але відмітимо, що і тут потрібно бути раціональним – якби ми ще ввели додаткові змінні для обчислення коренів квадратних, то від цього програма навряд чи стала б зрозумілішою, більше того, вона стала б більш не зрозумілою.
Задача 12 Округлити дробове число з заданою точністю.
Розв’язання : Зверніть увагу на формулювання задачі: нам потрібно округлити число з заданою точністю, а не вивести на екран з заданою точністю, тобто при подальших розрахунках нам, можливо, потрібно буде знову використовувати дане округлене число, а не його початкове значення.
Ідея округлення полягає в слідуючому:
- вводимо число;
- визначаємо, скільки знаків після коми нам потрібно мати;
- множимо дане число на 10 в степені кількість значущих цифр після коми;
- до отриманого числа застосовуємо функцію round;
- отримане число ділимо на 10 в степені кількість значущих цифр після коми.
Все на перший погляд просто, але нам потрібно знайти спосіб знаходження числа 10 в степені кількість значущих цифр після коми. Якби ми розв’язували цю задачу трохи пізніше, то проблем не було б, але в даний момент ми не знаємо ні операторів циклів, ні, навіть, умовного оператора. Тому на допомогу нам у цьому випадку приходить математика. У мові Паскаль немає операції піднесення до степеня (крім піднесення до квадрату), проте є дві функції, які можуть допомогти: exp(x) i ln(x), отже маємо програму:
program demoround;
var a,b,c : real;
n : byte;
begin
write('Введiть число: '); readln(a);
write('Скiльки знакiв пiсля коми залишити: '); readln(n);
b := a*exp(ln(10)*n); { множимо на 10n }
b := round(b); { округлюємо до цілих }
c := b*(exp(ln(10)*(-n))); { ділимо на 10n }
writeln('Шукана точнiсть ',c:2:n);
readln;
end.
Звертаємо увагу на використану формулу. З нею самостійно можуть розібратись лише учні випускних класів, іншим же рекомендуємо звернутись за консультацією до вчителів математики. Без цього вам важко буде самостійно розв’язати наступну задачу.
Задача 13 Самостійно адаптуйте дану програму для піднесення довільного числа до довільного степеня.
