Рнц «Курчатовский институт»
| Вид материала | Автореферат |
СодержаниеВ 5-й главе Н (Т) Рис.6. Зависимости В Измерения в серебре В бериллии Н (Т) Рис.8. Фазовая диаграмма на плоскости (Н Основные результаты работы Результаты диссертации |
- Курчатовский институт столяревский анатолий яковлевич хемотермические технологии аккумулирования, 716.09kb.
- Мониторинг Средств массовой информации по теме: Подписание Соглашения между Международной, 411.74kb.
- В. П. Смирнов Институт ядерного синтеза, рнц «Курчатовский институт», 20.41kb.
- Программа формируется на основе докладов, заказанных программным комитетом. Планируется, 17.64kb.
- Заев иван александрович, 263.62kb.
- А. В. Хмара рнц «Курчатовский институт», Москва, Россия, 15.66kb.
- Е. А. Сорокина, В. И. Ильгисонис рнц "Курчатовский институт", Москва,, 18.27kb.
- С. В. Коновалов ияс рнц «Курчатовский институт», Москва, Россия, e-mail, 13.58kb.
- Высокоинтенсивный ионный синтез, 57.15kb.
- О. С. Нарайкин Заместитель директора рнц «Курчатовский институт», Москва, 149.57kb.
Бериллиевый монокристалл, который исследовался ранее, представлял собой пластину с размерами 11x9x1,8мм3. Для измерения магнитострикции , то есть осцилляций размера образца
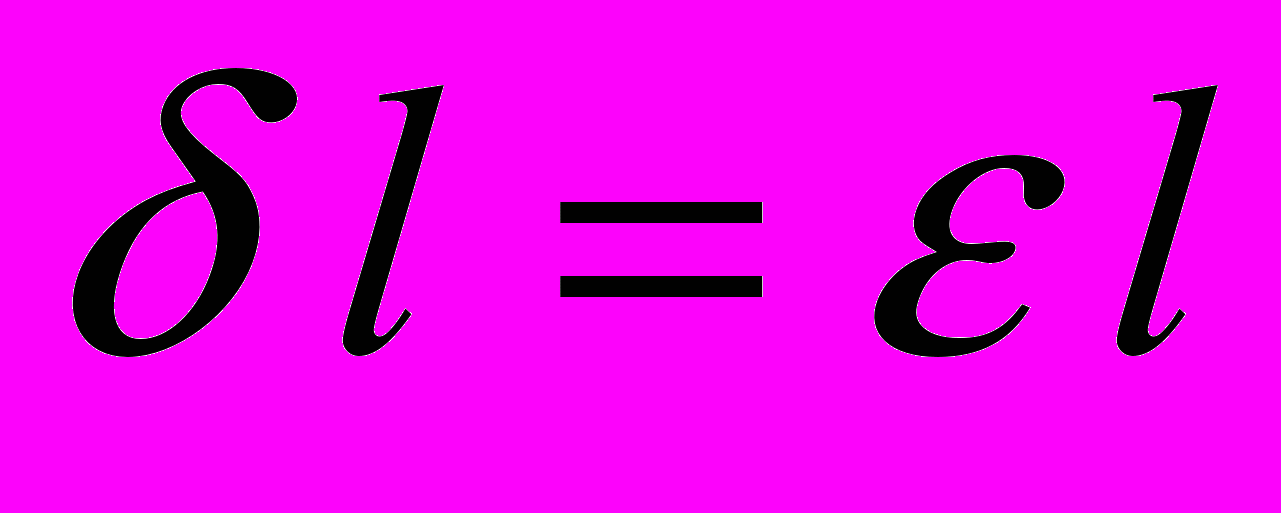вдоль его длинной стороны, использовался дилатометр, действующий по принципу измерения емкости плоского конденсатора. Подвижная обкладка была выполнена в виде подпружиненной пластины, в которую упирался образец. При помощи регулировочного винта можно было изменять расстояние между обкладками измерительного конденсатора и, соответственно, стартовую емкость. Измерения проводились как в жидком гелии (нормальном или сверхтекучем), так и в его парах. При этом результаты значительно различались уровнем и характером шумов. При прохождении уровня жидкого гелия через конденсатор наблюдался сильный дрейф емкости. Наиболее благоприятная ситуация для измерений была в парах гелия при Т=1.5 К, когда шум составлял ~0.510-3пФ, что соответствовало относительной деформации образца 
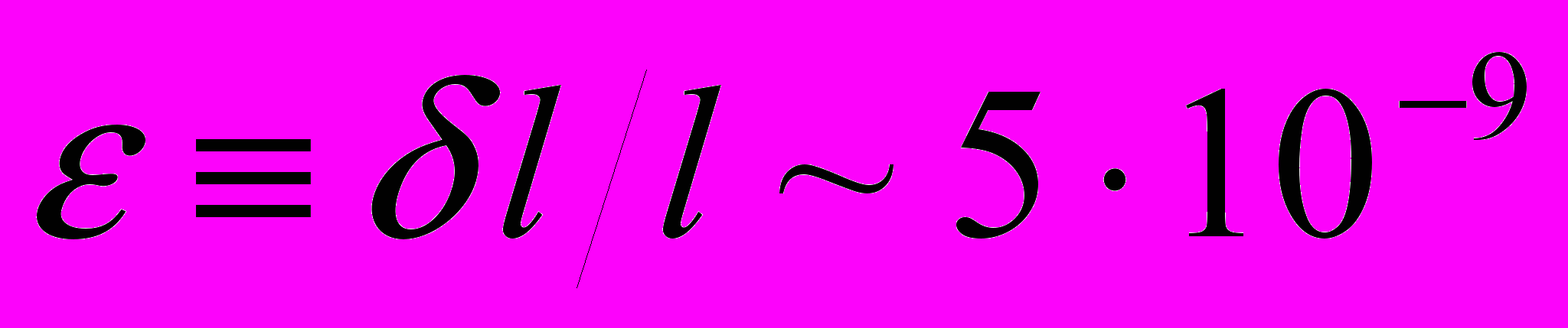.Измерения магнитострикции были проведены в магнитных полях от 10 до 70кЭ при гелиевых температурах, в том числе во всей области образования доменов. Зависимости магнитострикции при Т=4,2К, где нет доменов, почти идентичны осцилляциям магнитного момента с характерными для бериллия биениями. При Т=1.5 К в области доменного состояния появились характерные «провалы» в амплитуде, которые полностью исчезли, когда под медные острия, между которыми находился образец, были подложены медные же прокладки толщиной ~0,5мм. Такое поведение интерпретировалось как своеобразная локальная «сверхмягкость» при образовании двух фаз.
Измеренная величина стрикции позволила определить деформацию решётки в соседних фазах. Поскольку поверхность Ферми бериллия хорошо известна, удалось связать величину деформации с изменением плотности электронов в доменной стенке. Полученный результат с хорошей точностью соответствует известной из эксперимента разности магнитной индукции в доменах. Вопрос о механизме тока намагничения, таким образом, однозначно свёлся к магнитострикции, амплитуда которой обратно пропорциональна величине модуля Юнга. Поэтому этот вывод непосредственно связан с вопросом об электронном вкладе в сжимаемость металла. Показано, что с точностью до предположения о том, что весь ток в доменной стенке обусловлен градиентом плотности зарядов, сжимаемость металла или модуль Юнга целиком определяется набором констант, которые в свою очередь полностью определяются устройством поверхности Ферми.
С другой стороны, этот же вопрос о сжимаемости металла напрямую связан с вопросом об осцилляциях уровня Ферми в магнитном поле. Показано, что точная компенсация этих осцилляций в результате магнитострикции происходит в том и только в том случае, если сжимаемость металла полностью обусловлена сжимаемостью электронного газа. Этот факт, безусловно, играет важную роль в образовании диамагнитных доменов. Только в случае компенсации эффекта осцилляций уровня Ферми в соседних доменах отсутствует контактная разность потенциалов и отсутствует электрическое поле в доменной стенке. В противном случае возникновение дополнительной электростатической энергии, обусловленной этим полем, стало бы существенным препятствием для образования доменов. Найденное нами образование доменов Кондона во всех исследованных металлах говорит в пользу обсуждаемой компенсации.
Образование доменной структуры, состоящей из фаз различной плотности, позволяет понять обнаруженное явление «сверхмягкости». Под медным остриём, слегка прижатым к образцу бериллия, периодически образуется «ямка», глубина которой формально соответствует стократному уменьшению жёсткости материала. Эта ямка образуется только при образовании двухфазного состояния. В однородном состоянии ямка исчезает. Представляется естественным объяснить такое поведение как результат локальной перестройки доменной структуры под остриём.
Итак, в доменной стенке деформация приводит к избыточной упругой энергии. Поскольку состояния слева и справа от границы, которые соответствуют минимуму энергии, заданы, то задана величина скачка в размере ячейки слева и справа. Поэтому избыточная упругая энергия будет тем меньше, чем на большую толщину границы этот скачок будет размазан. Поэтому в больших магнитных полях, когда ларморовский радиус уменьшается, толщина доменной стенки может намного превзойти этот радиус, что и было получено в измерениях в серебре. С другой стороны, разница в размере ячейки накапливается вдоль доменной границы, поэтому с этой точки зрения длинные границы невыгодны. В плоскости пластины это ограничение можно обойти за счёт мозаичности ламинарной доменной структуры. Однако вдоль магнитного поля длина границы это толщина образца, и тут ничего не поделаешь, остаётся только увеличение толщины границы или некое усложнение структуры. В связи со сказанным, возможно, анизотропный характер магнитострикции в бериллии является причиной того, что домены Кондона отсутствуют на его поверхности.
В 5-й главе описывается первое экспериментальное обнаружение гистерезиса в эффекте дГвА в бериллии и его детальное исследование при помощи различных методов. Величина гистерезиса (коэрцитивная сила) оказалась очень мала, не больше 2 Гс, что на два порядка меньше величины периода дГвА. (В серебре гистерезис оказался порядка 0,2 Гс при величине периода 20 Гс). В случае прямого метода индукция в образце измерялась посредством миниатюрного датчика Холла, расположенного вплотную к торцу образца. Разумеется, измеряемая у торца величина немного отличается от индукции в центре (только для сверхпроводников 1-го рода В=0 в центре и на торце), однако ни для обнаружения эффекта, ни для измерения величины гистерезиса, то есть коэрцитивной силы, это не имеет принципиального значения. Более существенным является тот факт, что в сверхпроводящем соленоиде имеется собственный гистерезис, поэтому внешнее магнитное поле измерялось другим датчиком Холла, расположенном на достаточно далеком расстоянии от образца.
Надо сказать, что приведенные здесь данные (см. рис.6) получены при очень медленной развёртке поля, чтобы отношение сигнала к уровню шума было около 10, и в самой «благоприятной» обстановке - самая низкая температура и область максимальной амплитуды дГвА. В других областях магнитного поля и температуры получение такого результата становится затруднительным, а при приближении к фазовой границе диамагнитных доменов и вовсе невозможной. Другими словами, прямой метод оказывается недостаточно чувствительным, и его нельзя использовать для более детального исследования гистерезиса во всей области (Н,Т).
Гораздо более чувствительным оказался стандартный метод измерения магнитной восприимчивости с использованием модуляции внешнего магнитного поля. Образец располагается в одной из двух скомпенсированных катушек (pickup coil), а сигнал раскомпенсации, пропорциональный при достаточно малой амплитуде модуляции среднему наклону М(Н), то есть магнитной восприимчивости образца
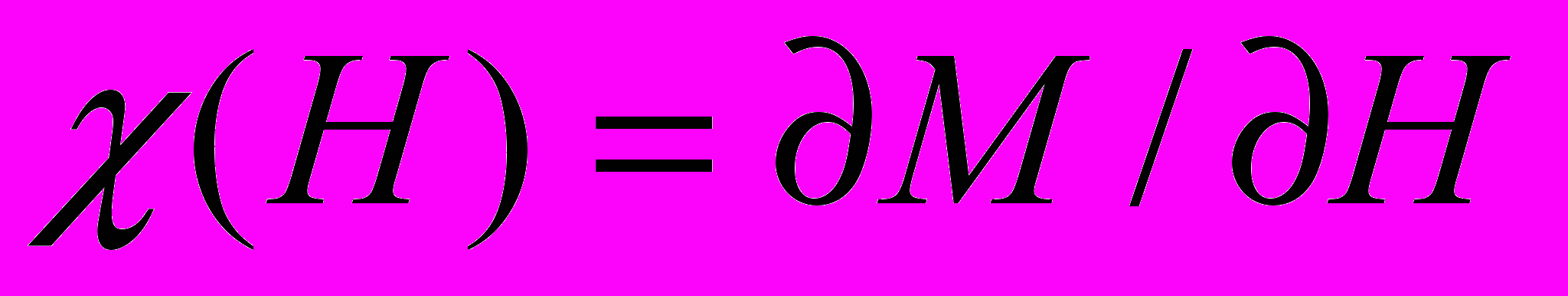, измеряется фазочувствительным вольтметром (lock-in). При дальнейшем уменьшении амплитуды модуляции амплитуда измеряемого сигнала соответственно падает, однако величина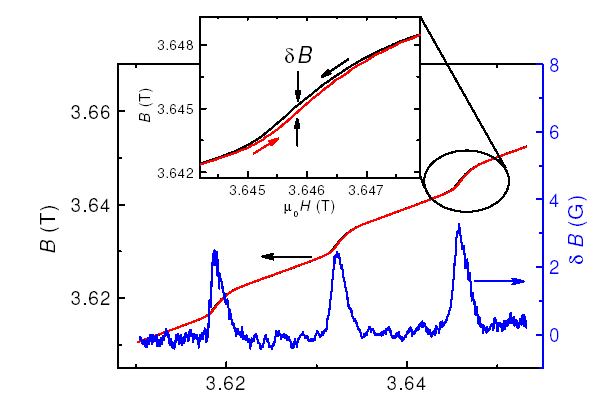
Н (Т)
Рис.6. Зависимости В(Н) вверх и вниз при температуре 1,3 К в области пучности амплитуды дГвА, измеренные датчиком Холла (шкала слева). В парамагнитной части каждого периода наблюдается гистерезис, показанный крупнее на вставке. Разница показаний δВ вверх и вниз по полю показана внизу (шкала справа).
нормализованного сигнала, то есть отнесённая к амплитуде модуляции, далее уже не меняется. Именно так и есть всегда при обратимой намагниченности. В случае возникновения гистерезиса всё иначе, особенно, если амплитуда модуляции становится меньше величины гистерезиса, т.е. коэрцитивной силы. Отклик на модуляционный сигнал становится кардинально нелинейным.
Причина в том, что как только частная петля намагниченности оказывается внутри полной, то есть всего гистерезиса, возникают три существенных следствия. Во-первых, уменьшается средний наклон в малой петле, то есть амплитуда 1-й гармоники, которая тут уже не соответствует восприимчивости. Во-вторых, отклик сдвигается по фазе (запаздывает), то есть появляется мнимая часть. В-третьих, форма сигнала отклика существенно меняется от синуса к меандру. В этом случае появляются нечётные гармоники и в первую очередь 3-я. Это происходит пороговым образом при возникновении гистерезиса после пересечения фазовой границы доменного состояния. Сказанное демонстрирует рис. 7.
Количественное изучение гистерезиса представляет большой интерес. Ясно, что гистерезис связан с характером движения доменных стенок, и с величиной энергетического барьера при образовании новой фазы. Зависимость
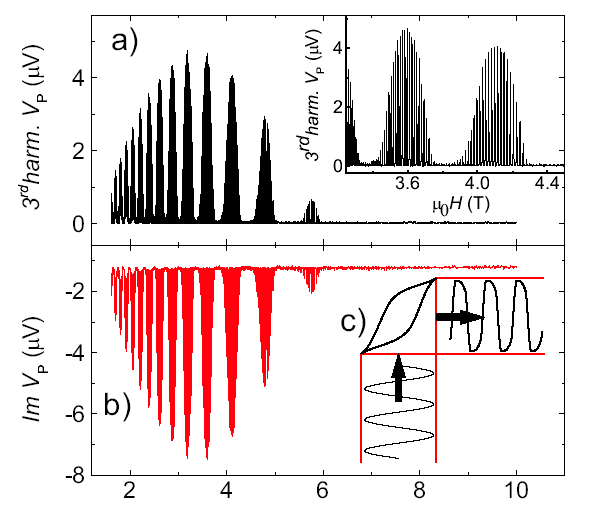
Рис.7. (a) Сигнал 3-й гармоники, на вставке тот же сигнал в увеличенном масштабе. (b) Мнимая часть отклика. Оба рисунка (a) и (b) при температуре Т=1,3 К и амплитуде модуляции 2,5 Гс. Вставка (c) демонстрирует схематически, как при возникновении гистерезиса сигнал отклика на синусоидальную модуляцию принимает форму меандра и сдвигается по фазе.
величины гистерезиса от магнитного поля и температуры может дать информацию об этом движении доменных стенок. Это может, в частности, пролить свет на вопрос об аномальном затухании геликонов в алюминии [5]. Кроме того, это поможет в построении более конкретной теории, поскольку до настоящего времени есть только идеализированная теория [12] без учёта реальной деформации решётки. Так, можно полагать, что необходимая деформация в доменной стенке является причиной её большой толщины. А это может быть причиной малого взаимодействия с точечными дефектами и, соответственно, малой величины гистерезиса. Несмотря на незавершённость понимания природы этого явления, мы имеем ряд существенных практических следствий.
(i) С появлением гистерезиса амплитуда 1-й гармоники, резко падает, как только амплитуда модуляции становится порядка или меньше ширины гистерезиса. Это приводит а) к неправильному измерению магнитной восприимчивости и б) к возможности измерить эту ширину, то есть коэрцитивную силу.
(ii) С появлением гистерезиса сигнал становится исключительно нелинейным с появлением в спектре сигнала отклика, сдвинутого на π/2, и резкого роста нечётных гармоник. Суммарный анализ нескольких вкладов в сигнал отклика даёт возможность восстановить размер и форму гистерезиса.
(iii) Пороговый характер возникновения в отклике 3-й гармоники и мнимой части и независимость возникновения в образце неустойчивости от его формы даёт возможность с большой точностью определять точку пересечения границы фазовой диаграммы состояния с диамагнитными доменами в данном металле с соответствующей данному образцу температурой Дингла.
Глава 6 посвящена описанию экспериментов по определению фазовой границы диамагнитных доменов в серебре и бериллии. Проблема заключалась в том, что уже полученные теоретические расчёты фазовой границы можно было сопоставлять только с отрывочными экспериментальными данными. Во всех случаях – и ЯМР, и μSR, и данные датчиков Холла, находясь внутри фазовой диаграммы, подтверждали существование доменов, но точное положение границы раздела фаз оставалось далеко в стороне от возможностей отмеченных методик, поскольку вблизи границы величина ΔВ стремится к нулю и становится недоступной для измерения. Тем не менее в серебре все полученные результаты находились в полном согласии с расчётами по формуле ЛК [13], что объяснялось близостью к сфере поверхности Ферми серебра. Напротив, данные μSR для бериллия противоречили имеющимся к тому времени расчётам. Это послужило основанием для корректировки фазовой диаграммы [14]. В предыдущей главе было показано, что возникновение гистерезиса при переходе к двухфазному состоянию приводит к кардинально нелинейному отклику на модуляцию магнитного поля, что может быть использовано для весьма точного нахождения местоположения фазовой границы.
Измерения в серебре проводились на образце из той же серии, что и образец, использованный в главе 3. Фазовая диаграмма в серебре простирается в область сверхсильных магнитных полей, поэтому эксперименты проводились как в сверхпроводящих соленоидах, так и в резистивном магните до 30 Т. При этом данные в разных соленоидах перекрывались.
Появление гистерезиса влечёт за собой несколько следствий, каждое из которых может быть, в принципе использовано для определения точки пересечения фазовой границы. Имея в виду, что измерения в больших полях резистивного магнита из-за повышенных шумов и значительно меньшей однородности поля могут представить определённые затруднения, были для сравнения использованы все описанные выше в предыдущей главе способы фиксации появления гистерезиса.
Каждый из этих эффектов измерялся по отдельности в одних и тех же условиях, то есть каждый раз при Т=2,7 К находилась соответствующая величина критического поля, соответствующая пересечении границы. Были изучены 4 способа: падение амплитуды 1-й гармоники, появление мнимой части, появление 3-й гармоники и появление фазы 3-й гармоники. Затем результаты сравнивались. Отличия составили +/- 4%. Наименее отчётливо переход фиксируется по мнимой части сигнала, которая присутствует в серебре в отличие от бериллия и в однородном состоянии, что обусловлено большой проводимостью серебра и, соответственно, наведенными токами в образце (eddy currents). Наиболее простым и точным оказался метод измерения 3-й гармоники. В отдельных экспериментах проверялась «устойчивость» полученной точки к изменению в широких пределах (в 4 раза) частоты и амплитуды модуляции. Это особенно успешно использовалось при измерениях в резистивном магните, где уровень шумов значительно выше, чем в сверхпроводящем соленоиде.
Из полученных результатов можно констатировать прекрасное согласие эксперимента в серебре с расчётом по теории ЛК с температурой Дингла 0,2 К, то есть поверхность Ферми серебра в силу своей сферической формы прекрасно описывается количественно теорией ЛК. Итак, возникновение гистерезиса при переходе к двухфазному состоянию даёт простой и надёжный метод экспериментального определения фазовой диаграммы диамагнитных доменов. При этом на металлах с большой проводимостью предпочтительным способом является измерение 3-й гармоники. На металлах с большим сопротивлением (бериллий) можно ограничится 1-й гармоникой, регистрируя появление мнимой части в отклике.
В бериллии фазовая диаграмма доменного состояния оказывается в магнитных полях меньше 7 Т, поэтому все измерения производились в сверхпроводящем соленоиде. Основные результаты были получены при измерении 1-й гармоники отклика, амплитуда которой резко возрастает при пересечении фазовой границы. Как правило, измерения проводились, как и в серебре, изменяя магнитное поле при заданной температуре. В этом случае точка пересечения определялась с точностью до одного периода осцилляций. Однако вблизи верхушки фазовой диаграммы для пучностей амплитуды (Н~4 Т, T~3 K) и таковой для узлов (Н~2,5 T, T~1,5 K) пересечение фазовой границы производилось «вертикально», то есть, изменяя температуру при заданном магнитном поле точно в центре дГвА периода.
Эксперименты на удлинённом образце и на образце в форме пластинки (с такой же температурой Дингла) показали ровно такой же результат. Полученная фазовая диаграмма прекрасно согласуется с данными µSR, полученными ранее. Сравнение с теоретическим расчётом показывает хорошее согласие в области полей 2-3 Т, но только для пучностей. Главное противоречие с теорией имеет место в больших магнитных полях. Домены исчезают значительно раньше, чем в расчёте [14].
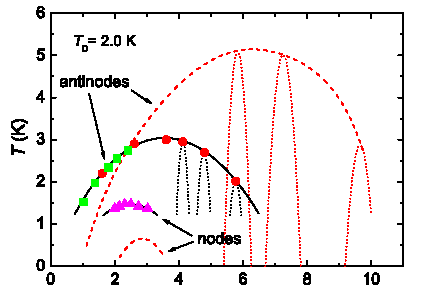
Н (Т)
Рис.8. Фазовая диаграмма на плоскости (Н,Т) для бериллия с TD=2,0 K. Показана фазовая граница как для пучностей (antinodes), так и для узлов (nodes). Кружки и треугольники получены при «вертикальном», квадратики – при «горизонтальном» пересечении границы. Пунктирные линии - результат расчёта [14].
Основные результаты работы.
Впервые использована техника μSR для изучения диамагнитных доменов. Обнаружено возникновение доменов Кондона в бериллии, олове, свинце, индии и алюминии, то есть во всех исследованных металлах. Тем самым установлена универсальность этого явления для всех металлов.
Впервые была обоснована и продемонстрирована на всех металлах возможность надёжной регистрации доменов лишь по осцилляциям полевой зависимости затухания λ(Н).
Впервые показано, что при достаточно низкой температуре домены возникают при амплитуде эффекта дГвА значительно меньшей величины полу периода. При этом и расщепление ∆В оказывается на порядок меньше полупериода, и значения индукции в диа- и парамагнитной фазах смещаются при изменении внешнего поля. (В бериллии и серебре они практически постоянны). На олове впервые обнаружено возникновение доменов Кондона на двух сечениях поверхности Ферми.
Впервые проведены измерения доменной структуры па поверхности монокристалла серебра при помощи миниатюрных датчиков Холла. Величина обнаруженной неоднородности индукции ∆В на поверхности в согласии с результатом Кондона практически совпала с таковой в объёме. Полученные поперечные размеры доменной структуры в серебре при 10 Т, а именно периода p≥150 мкм и толщины доменной стенки w≥20 мкм, оказались гораздо больше, чем ожидалось в соответствии с существовавшей теорией [15], то есть p~30 мкм, w~1 мкм.
Проведенные измерения при помощи датчиков Холла положения фазовой границы в серебре оказались в прекрасном согласии с теорией ЛК, что объясняется близостью Ферми поверхности серебра к сфере.
Проведены аналогичные тщательные эксперименты с использованием этих же датчиков на поверхности бериллия, где ожидаемая величина ∆В на порядок больше, чем в серебре. Главный вывод - домены Кондона существуют в бериллии только в глубине образца. По-видимому, именно этот факт является основной причиной неудачных поисков доменов Кондона в бериллии, в том числе и методом ЯМР.
Впервые измерена магнитострикция бериллия в условиях образования диамагнитных доменов. Показано, что фазам с противоположной намагниченностью соответствует и противоположная деформация решётки с противоположным изменением плотности электронов. В результате градиент плотности зарядов в доменной стенке обеспечивает в магнитном поле ток намагниченности, необходимый для разницы индукции в соседних фазах. Факт деформации решётки в доменной стенке качественно объясняет расхождение с теорией полученных результатов в серебре, а также отсутствие доменов на поверхности бериллия.
Показано, что точная компенсация осцилляций уровня Ферми в результате магнитострикции происходит в том и только в том случае, если сжимаемость металла полностью обусловлена сжимаемостью электронного газа.
Обнаруженное явление «сверхмягкости» удалось на основании эксперимента объяснить как результат локальной перестройки под медным остриём доменной структуры, состоящей из фаз различной плотности.
Впервые обнаружен гистерезис в эффекте дГвА, возникающий в состоянии с диамагнитными доменами. Найдена его величина. В бериллии это около 2 Гс при величине периода 200 Гс, и в серебре - около 0,2 Гс при величине периода 20 Гс. Вместе с тем обнаружено кардинальное изменение сигнала отклика в стандартном модуляционном методе измерения восприимчивости при образовании двухфазного состояния, в том числе пороговый рост 3-й гармоники.
Появлением гистерезиса, наконец, впервые объяснён известный эффект Плуммера, не находивший объяснения до сих пор.
Пороговый характер изменения отклика при пересечении фазовой границы доменного состояния впервые использован для точного экспериментального нахождения фазовой диаграммы доменов Кондона в серебре и бериллии. На основании полученных данных построены фазовые диаграммы доменов в серебре вплоть до 28 Т и в бериллии во всей области полей и температур до 1,3 К. Констатируется прекрасное согласие с теоретическими расчётами для серебра и существенное расхождение с расчётами для бериллия, особенно в области больших магнитных полей.
Результаты диссертации опубликованы в следующих статьях:
1. N. E. Alekseevskij, V. S. Egorov, A. A. Slutskin. Magnetic Breakdown in Beryllium. Journ. of Low. Phys., v.5, 377-396 (1971).
2. В.С.Егоров. О магнитопробойных траекториях в бериллии.
ЖЭТФ, т.69, 2231-2235 (1975).
3. В.С.Егоров. О влиянии диамагнетизма сверхпроводящей обмотки соленоида на его магнитное поле. Препринт ИАЭ-2754 (1976).
4. В.С.Егоров. Квантовые осцилляции термоэдс в условиях магнитного пробоя. ЖЭТФ, т.72, 2210-2234 (1977).
5. В.С.Егоров. Аномальная амплитуда эффекта де Гааза – ван Альфена квазидвумерного электронного газа (бериллий).
ФТТ, т.30, 1253-1257 (1988).
6. A. A. Varlamov, V. S. Egorov, A. V. Pantsulaya. Kinetic properties of metals near electronic topological transitions (2½ - order transitions). Review.
Advances in Physics. v.38, 469-564 (1989).
7. В.С.Егоров. Образование неравновесных электронов вблизи поверхности металла и их влияние на явления переноса при низких температурах.
ФТТ, т.32, 684-688 (1990).
8. В.С.Егоров. Электронные свойства металлов и сплавов.
B справочнике "Физические величины", под ред. И.С.Григорьева и Е.З.Мейлихова , (М., "Энергоатомиздат", 1991).
9. G.Solt, C.Baines, V.S.Egorov, D.Herlach, E.Krasnoperov, U.Zimmermann. Observation diamagnetic domains in beryllium by muon spin rotation spectroscopy.
Phys. Rev. Lett., v.76, 2575-2579 (1996).
10. G.Solt, C.Baines, V.S.Egorov, D.Herlach, E.Krasnoperov, U.Zimmermann. Direct evidence for dia- and paramagnetic domais in beryllium.
Hyperfine Interactions, v.104, 257-264 (1997).
11. В.С. Егоров, Е.П. Красноперов, Ф.В. Лыков, Г. Шолт, К. Байнс, Д. Герлах,
У. Циммерманн. Наблюдение диамагнитных доменов в бериллии.
ФТТ, т.40, 524-527 (1998).
12. G.Solt, C.Baines, V.S.Egorov, D.Herlach, U.Zimmermann. Diamagnetic domains in beryllium observed by muon-spin-rotation spectroscopy.
Phys.Rev. B 59, 6834-6846 (1999).
13. V.S.Egorov, G.Solt, C.Baines, D.Herlach, U.Zimmermann. Superconducting Intermediate State in white tin studied by muon-spin-rotation spectroscopy.
Phys. Rev. B 64, 024524-024529 (2001).
14. V.S.Egorov, G.Solt, C.Baines, D.Herlach, U.Zimmermann. Superconducting Intermediat State in white tin near Hc – new results by µSR.
Physica B, vv.289-290, 393-396 (2000).
15. В.С.Егоров, Ф.В.Лыков, О.А.Репина. Аномальная сжимаемость и магнитострикция бериллия в условиях образования диамагнитных доменов.
Письма в ЖЭТФ, т.72, 28-33 (2000).
16. V.S.Egorov. Effect of the boundary conditions on the two-dimensional electron gas and the quantum Hall effect.
Physica B, v.301, 212-221 (2001).
17. G.Solt, V.S.Egorov. Recent results on Condon Domains in metals. Review.
Physica B, v.318, 231-250 (2002).
18. В.С.Егоров, Ф.В.Лыков. Диамагнитные домены и магнитострикция в бериллии.
ЖЭТФ, т.94, 162-171 (2002).
19. V.S.Egorov. Condon Domains – these non-magnetic diamagnetic domains.
HAIT J. of Science and Engineering, v.1, 647-673 (2004).
20. R.B.G.Kramer, V.S.Egorov, A.Gordon, N.Logoboy, W.Joss, V.A.Gasparov. “Magnetic” phase transition in silver.
Physica B, v.362, 50-56 (2005).
21. R.B.G.Kramer, V.S.Egorov, A.G.Jansen, W.Joss. Hysteresis in de Haas – van Alphen effect.
Phys.Rev.Lett., v.95, 187204-187208 (2005).
22. R.B.G.Kramer, V.S.Egorov, V.A.Gasparov, A.G.Jansen, W.Joss. Direct observation of Condon domains in silver by Hall probes.
Phys.Rev.Lett., v.95, 267209-267213 (2005).
23. R.B.G.Kramer, V.S.Egorov, V.A.Gasparov, A.G.M.Jansen, W.Joss. High Magnetic field measurements of Condon domain phase diagram for silver.
Journ. of Magnetism and Magnetic Materials (2006).
24. R.B.G.Kramer, V.S.Egorov, A.G.Jansen, W.Joss. Hysteresis in de Haas – van Alphen Effect.
Journ. of Magnetism and Magnetic Materials (2006).
Цитированная литература
[1]. J.H.Condon, Phys. Rev., vol.145, (1966), p.526-535.
[2]. L.Landau, Zeitschrift fur Phys., vol.64, (1930), p.629-637.
[3]. И.М.Лифшиц, А.М.Косевич, ЖЭТФ, т.29, (1955), с.730-752.
[4]. Д.Шенберг, Магнитные осцилляции в металлах. М., Мир, 1986, 678 стр.
[5]. В.И.Божко, Е.П.Вольский, Письма в ЖЭТФ, 26, в.4, 337 (1977).
[6]. A. Gordon, I.D. Vagner and P. Wyder, Solid St. Comm., 87, 12, 1155-1158 (1993).
[7]. A.Schenck, Muon Spin Rotation Spectroscopy, Hilger, Bristol, 1986.
[8]. Ю.М.Белоусов, В.П.Смилга, ФТТ, т.21, 2459-2462 (1979).
[9].И.М.Лифшиц, ЖЭТФ, т.33, 1569 (1960).
[10]. J.D.Livingstone and W. de Sorbo, in Superconductivity, ed. by R.D.Parks, (Dekker, New York, 1969), v.2, pp.1235-1281.
[11]. А. Франк-Каменецкий, “Лекции по физике плазмы ”, М., Атомиздат (1968).
[12]. A.Gordon, N.Logoboy, W.Joss, Phys. Rev. B 69, 174417 (2004).
[13]. A.Gordon, M.A.Itskovsky, P.Wyder, Phys. Rev. B 59, 10864 (1999).
[14]. G.Solt, Solid St. Comm., v.118, 231 (2001).
[15]. А.А.Абрикосов, “Основы теории металлов”, М., “Наука” (1987)
И.А.Привороцкий, ЖЭТФ, т.52, 1755 (1967).