Расчетно-пояснительная записка
| Вид материала | Пояснительная записка |
- Государственная Академия Управления имени С. Орджоникидзе Институт национальной и мировой, 399.35kb.
- Расчетно-пояснительная записка, 642.73kb.
- Расчетно-пояснительная записка к курсовому проекту по технологии литейного производства, 340.29kb.
- Группа 2440 расчётно-пояснительная записка к курсовой работе по направленному бурению, 787.94kb.
- Расчетно пояснительная записка, 307.05kb.
- Расчетно пояснительная записка, 312.13kb.
- Расчетно-пояснительная записка содержит: 111 страниц, 12 таблиц, 16 рисунков, 58 источников., 10.29kb.
- Кафедра Вычислительной Техники Расчётно-пояснительная записка, 484.99kb.
- Расчётно-пояснительная записка к курсовому проекту по дисциплине: "Теория механизмов, 22.29kb.
- Н. П. Огарёва факультет светотехнический Кафедра экономики и управления на предприятии, 529.21kb.
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Московский государственный технический университет имени Н. Э. Баумана»
(МГТУ им. Н. Э. Баумана)
Факультет: «Аэрокосмический»
Кафедра: «Компьютерные системы и сети»
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
курсовой работы на тему
«ПОИСК ОПТИМАЛЬНОЙ КОНФИГУРАЦИИ СТРУКТУРЫ СЕТИ ДЛЯ РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ»
по курсу “Вычислительные системы”
Листов 22
Руководитель,
к.т.н., доц. Ю. М. Руденко
Исполнитель,
студ. гр. АК5-101 С. А. Туркин
2008
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Московский государственный технический университет имени Н. Э. Баумана»
(МГТУ им. Н. Э. Баумана)
Факультет Аэрокосмический
Кафедра Компьютерные системы и сети_____
ЗАДАНИЕ
на курсовую работу
по курсу __Вычислительные системы____________________________________________
Студент: __Туркин С.А. АК5-101________________________________________________
Руководитель: __Руденко Ю. М.__________________________________________________
Защита проекта: ______________________ 2008 г.
I. Тема работы: Поиск оптимальной конфигурации структуры вычислительной сети для решения поставленной задачи.
II. Техническое задание:
- Получить треугольную матрицу следования 40х40 со скалярными весами для ИГ с помощью датчика псевдослучайных чисел. Инициализирующее значение датчика случайных чисел вводится в диалоге.
- Задать в диалоге количество логических операторов в графе, представленном полученной матрицей, заменив произвольные вершины графа логическими, что в итоге формирует исходный ИЛГ.
- Структура вычислительной сети – двоичный гиперкуб.
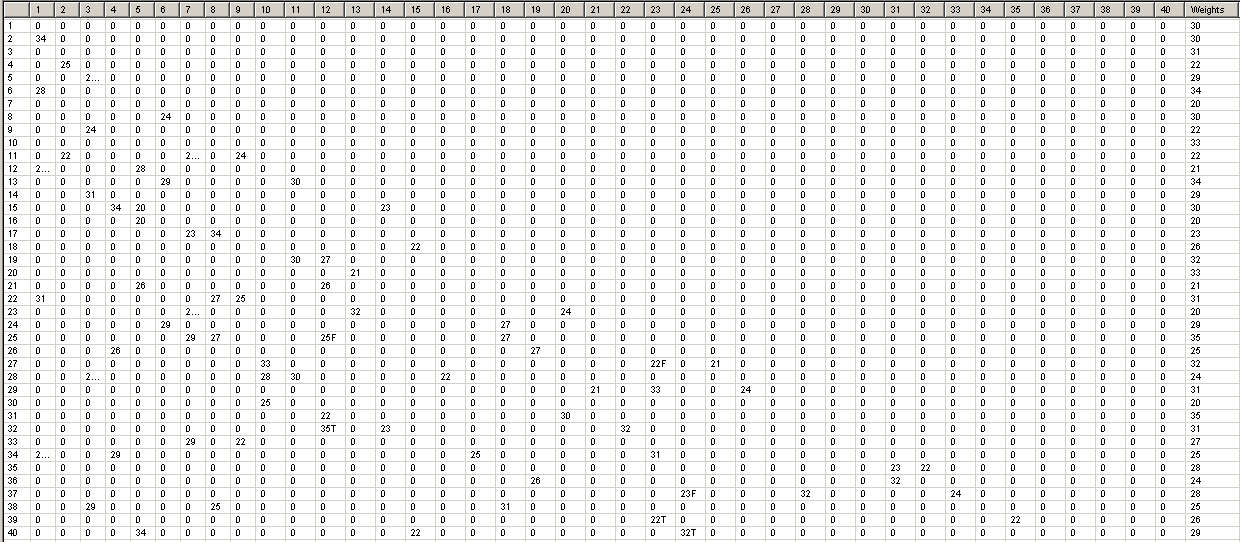
- Минимизировать количество узлов вычислительной сети, учитывая весь набор ИГ, получаемых из ИЛГ при минимальном времени решения задачи. Матрица смежности задачи имеет следующий вид:
III. Объем и содержание работы: Расчетно-пояснительная записка на 20 - 30 листах формата А4, программные модули с исходными текстами программы на дискете.
Расчетная часть: В расчетно-пояснительной записке привести описание работы программы, основных алгоритмов, а также используемых структур данных.
Программная часть: Программа должна быть оснащена соответствующим интерфейсом для удобства работы пользователя. Исходные тексты программных модулей должны содержать все необходимые комментарии.
Руководитель проекта: Руденко Ю. М. _______________
Дата выдачи «7» февраля 2008 г.
Содержание
Введение 5
1 Постановка задачи 6
2 Анализ исходных данных 6
3 Описание структуры вычислительной сети 8
4 Описание алгоритмов 9
4.1 Основные определения 9
4.2 Алгоритм разбиения задачи, представленной ИЛГ, на подзадачи, представимые ИГ. 11
4.3Алгоритм разбиения задачи, представленной ИГ, на нити. 11
4.4 Алгоритм уплотнения нитей задачи. 12
4.5 Алгоритм распределения нитей по узлам вычислительной сети. 14
5 Описание интерфейса программы. 15
Заключение 21
Список использованных источников 22
Введение
В настоящее время усилилась тенденция использования многопроцессорных систем для обработки данных. Для эффективного использования таких систем необходимо, во-первых, преобразовывать последовательные алгоритмы обработки данных в параллельные, а во-вторых, использовать специальные алгоритмы, которые позволят распределить операторы параллельных алгоритмов по процессорам вычислительной сети.
Разработка алгоритмов разбиения задачи на участки, способные к параллельному выполнению, и планирования их выполнения на ВС связана с рядом трудностей. В частности, необходимо проанализировать большое количество условий, учесть множество различных ситуаций, которые возникают при распределении операторов по нитям и нитей по процессорам ВС. Очень часто такие алгоритмы подразумевают полный перебор всех возможных вариантов, что значительно увеличивает время их работы. Кроме того, необходимы точные исходные данные, такие как времена расчета отдельно взятых операторов, объем передаваемых данных между ними. Необходимо также знать времена передачи данных между процессорами в структуре ВС.
При этом возникают различные задачи, одной из которых является задача поиска оптимальной конфигурации вычислительной сети. Здесь предполагается, что структура вычислительной сети задается изначально и не подлежит модификации, но параметры этой структуры варьируются с целью получения оптимального варианта. Решение данной задачи позволит эффективно использовать наращиваемые многопроцессорные вычислительные модули.
.
1 Постановка задачи
Цель – определить оптимальную конфигурацию ВС, имеющей структуру n-мерного двоичного гиперкуба, для решения вычислительной задачи, матрица смежности которой генерируется согласно заданному алгоритму.
Для достижения этой цели необходимо разработать и реализовать алгоритм разбиения задачи, представленной ИЛГ, на подзадачи, представленные ИГ, алгоритм разбиения задачи, представленной ИГ, на нити, алгоритм уплотнения нитей задачи, представленной ИГ, алгоритм распределения нитей задачи, представленной ИГ, по узлам вычислительной сети, при условии минимизации затрат на передачу данных между узлами сети.
Реализация алгоритмов должна быть выполнена в рамках отдельной программы, которая должна обеспечивать:
- Возможность ввода размерности задачи, инициализирующего значения счетчика случайных чисел, число логических операторов в задаче. Это придает программе большую универсальность и удобство в использовании.
- Возможность графического отображения матриц смежности задачи и отдельных подзадач, результатов разбиения подзадач на нити и распределения их по узлам вычислительной сети, а также возможность визуализации графов задачи и подзадач.
2 Анализ исходных данных
Матрица смежности решаемой задачи генерируется по заданному алгоритму программой. Полученная матрица представлена на рис. 2.1.

Рис. 2.1. Матрица смежности решаемой задачи.
Алгоритм генерации матрицы смежности учитывает необходимость построения верхнетреугольной матрицы, отсутствие циклов в ИГ, представляющем задачу, равномерное распределение вершин ИГ по уровням, ограничение в величинах весов как по верхней границе, так и по нижней.
Информационный граф, представляющий решаемую задачу, показан на рис. 2.2.
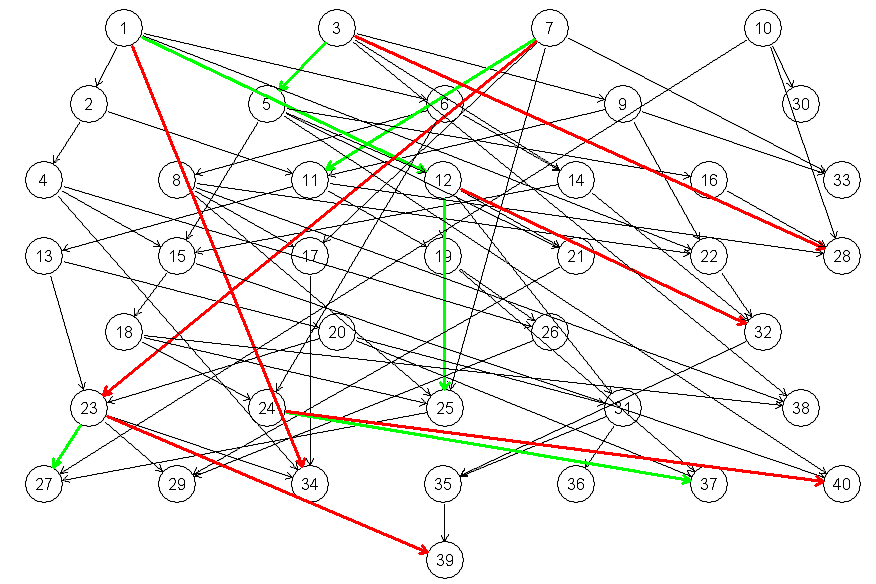
Рис. 2.2 - Информационный граф решаемой задачи
Красными стрелками обозначены переходы, соответствующие условию Истина, зелеными – Ложь. Веса вершин и дуг не показаны, чтобы не загромождать рисунок. При необходимости их всегда можно посмотреть в матрице смежности.
3 Описание структуры вычислительной сети
Для решения задачи используется ВС со структурой n-мерного двоичного гиперкуба.
Коммутационная структура типа n-мерный двоичный гиперкуб описывается следующими соотношениями:
- вершины имеют номера Ni=2p, p=0,1,…n-1, где n – размерность гиперкуба;
- каждая вершина Vi задана двоичным числом
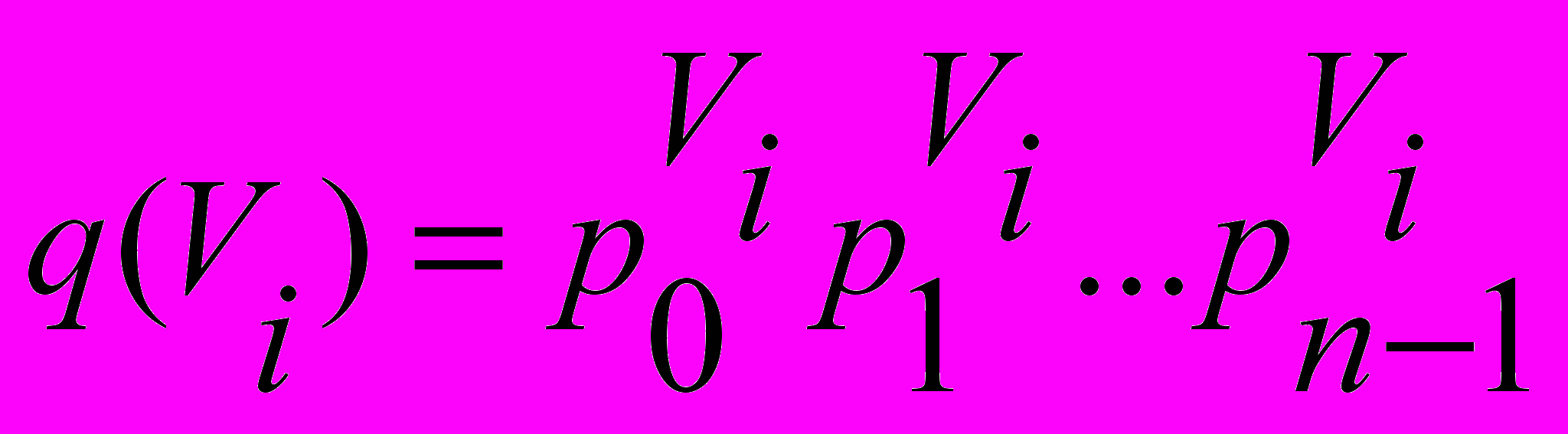 ;
;- между вершинами Vi и Uj проводится ребро, если их двоичные номера q(Vi) и q(Vj) различаются только одним разрядом.
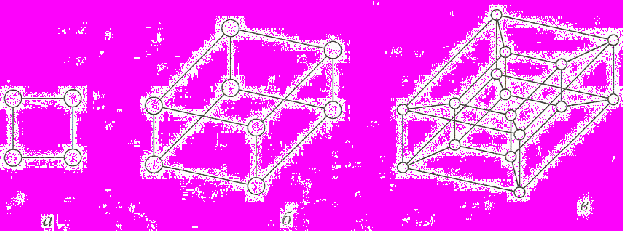
Рис. 3.1 – Пример представления булевых кубов: а – размерности 2, б – размерности 3, в – размерности 4
Как видно из описания, единственным варьируемым параметром такой структуры является n – размерность гиперкуба. В алгоритме распределения нитей по вершинам ВС этот параметр изменяется с целью поиска структуры ВС, оптимальной для решения задачи.
4 Описание алгоритмов
4.1 Основные определения
Вершина - оператор информационного графа заданной задачи.
Вес вершины (pV) – время вершины на i-ом процессоре.
Время старта вершины (Vs) – время старта расчета вершины в существующем разбиении вершин между процессорами.
Время финиша вершины (Vf) - время финиша расчета вершины в существующем разбиении вершин между процессорами.
Начальная и конечная вершины добавляются к информационному графу. Начальная вершина имеет номер 0 и необходима для того, чтобы граф имел одну точку входа. Конечная вершина имен номер N+1, где N – размерность матрицы следования исходного информационного графа, и необходима, чтобы граф имел одну точку выхода. Веса этих вершин равны нулю. Веса дуг, выходящих из нулевой вершины равны единице. После этого добавления исходная матрица следования S преобразуется, будет иметь размер N+2 и обозначаться C.
Высота вершины (h) – максимальное время от начала выполнения вершины до конца выполнения алгоритма, заданного матрицей следования С.
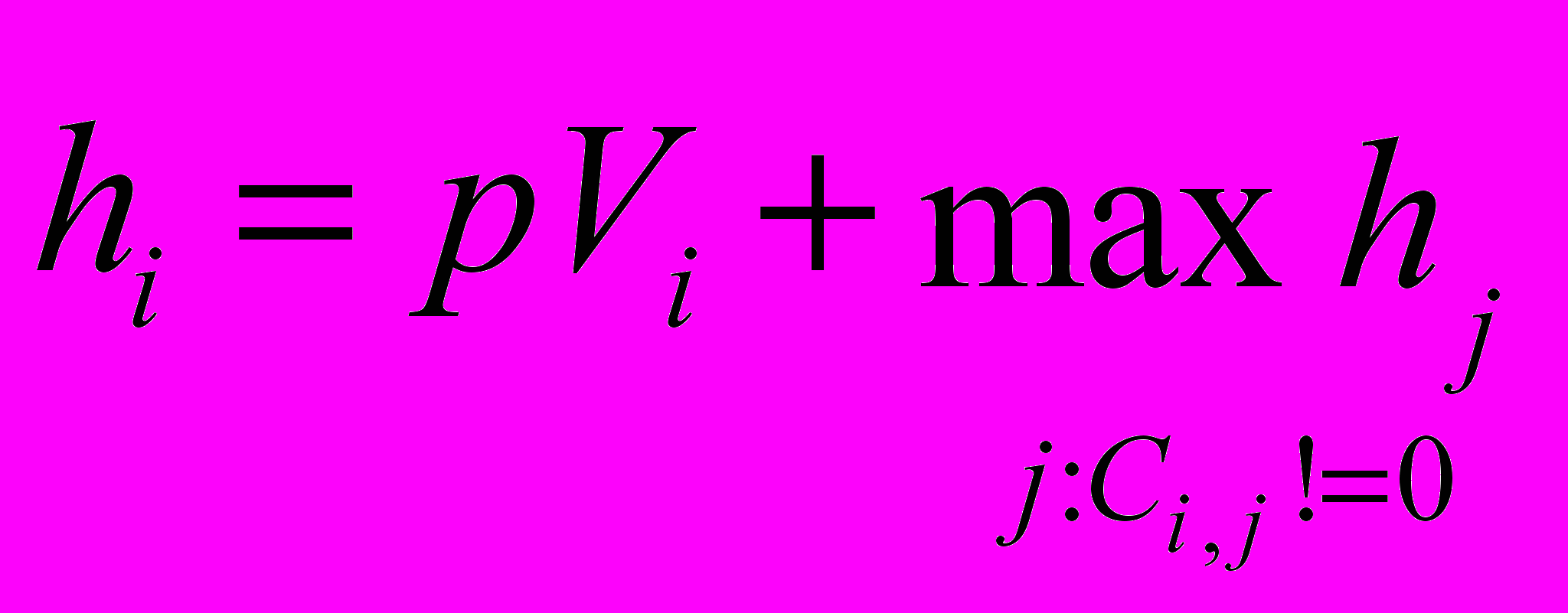
По определению высота конечной вершины равна нулю.
Родители вершины – все предшествующие данной вершине вершины, от которых она зависит по данным.
Нить – набор из одной или нескольких вершин, которые последовательно рассчитываются на одном процессоре.
Родительские нити вершины – набор нитей, каждая из которых содержат одного или нескольких родителей данной вершины
Время готовности вершины (r) – максимум из времен финиша всех родителей вершины.
Время старта нити (sT) – время старта нити в существующем разбиении нитей между процессорами.
Время финиша нити (fT) - время финиша нити в существующем разбиении нитей между процессорами.
Номер процессора нити (nfp) – номер процессора, на котором рассчитывается нить в существующем разбиении.
Матрица дистанций (ProcDistance) – матрица, содержащая расстояния между всеми процессорами заданной структуры вычислительной сети.
Массив активности (arActiveNodes) – массив размерности, равной размерности матрицы следования. Если i-й элемент равен 1, значит i-й оператор может выполняться при текущих значениях логических операторов. Если i-й элемент равен 0, значит i-й оператор не может выполняться при текущих значениях логических операторов.
Массив корневых элементов (arRootNodes) – массив элементов, которые имеют нулевые строки в матрице следования задачи.
Потомок элемента (узла) – элемент (узел) в который ведет связь из текущего элемента (узла).
Массив распределения операторов по нитям (arThreads) – массив размерности, равной размерности матрицы следования. Значение i-го элемента массива определяет номер нити, к которой принадлежит i-й оператор.
Массив распределения операторов по нитям после процедуры уплотнения (arPackThreads) – то же что и arThreads, но только после процедуры уплотнения.
Массив поздних сроков начала выполнения операторов (arLastTimes) – массив размерности, равной размерности матрицы следования. Значение i-го элемента массива определяет момент времени, не позже которого оператор должен начать выполняться, чтобы время решения задачи было равно критическому пути в графе.
4.2 Алгоритм разбиения задачи, представленной ИЛГ, на подзадачи, представимые ИГ.
Исходные данные на входе алгоритма: матрица следования S информационно-логического графа заданной задачи.
Данные на выходе: матрицы смежности отдельных подзадач, полученные разбиением ИЛГ на ИГ.
- Построить массив arRootNodes.
- Если есть еще не проанализированный набор значений всех логических операторов задачи, переходим на шаг 3, иначе на шаг 10.
- Инициализировать arActiveNodes единицами (т.е. изначально считаем, что все операторы могут выполняться).
- Очистить список элементов текущей подзадачи.
- Для текущего набора значений логического оператора найти массив операторов, которые не могут выполняться. В соответствующих позициях массива arActiveNodes поставить нулевое значение.
- Взять очередной элемент в массиве arRootNodes. Если все элементы просмотрены, перейти на шаг 8, иначе – на следующий шаг.
- Если текущий элемент активен, добавить его в список текущей подзадачи, и для всех потомков текущего элемента выполнить шаг 7. Перейти на шаг 6.
- Просматривая матрицу следования и список элементов текущей подзадачи сформировать матрицу следования текущей подзадачи.
- Изменить номер подзадачи. Перейти на шаг 2.
- Конец алгоритма.
-
Алгоритм разбиения задачи, представленной ИГ, на нити.
Данные на входе алгоритма: матрица следования задачи, представленной ИГ.
Данные на выходе процедуры: массив распределения операторов на нитям arThreads.
Описание алгоритма:
Основная идея алгоритма разбиения задачи на нити – минимизировать затраты на межпроцессорное взаимодействие. Тогда, если считать, что ненулевое значение элемента i-й строки и j-го столбца матрицы следования определяет принадлежность i-го и j-го оператора к одной нити, то постановка задачи разбиения задачи на нити примет следующий вид:
Исходная задача задана матрицей следования S. Ненулевой элемент на пересечении i-го и j-го столбца говорит о принадлежности i-го и j-го операторов одной нити (т.е. в исходной задаче возможны ситуации, когда один оператор принадлежит нескольким нитям одновременно). Необходимо построить задачу с матрицей следования S1, полученной из матрицы S, у которой на в каждом столбце и каждой строке было не более 1 ненулевого элемента. При этом исключение остальных ненулевых элементов происходит с учетом необходимости минимизации межпроцессорного взаимодействия.
Используемые обозначения:
MatrixSize – размер матрицы следования.
pRoot – корень бинарного дерева
1. Всем элементам массива arThreads присвоить значение -1.
2. Установить номер текущей нити ThreadNum := 0.
3. Из ненулевых элементов матрицы следования построить бинарное дерево l_tree, которое упорядочивает ненулевые элементы матрицы следования.
4. Построить новую матрицу следования S1 и заполнить все ее элементы нулями.
5. FoundAmount := 0;
6. Если FoundAmount < MatrixSize перейти на шаг 6, иначе на шаг 9.
7. Найти наибольший элемент дерева l_tree a. Исключить его из дерева. Определить номера строки i и столбца j матрицы следования S, которым соответствует текущий элемент.
8. Если в строке i или в столбце j матрицы S1 уже присутствует ненулевой элемент, тогда перейти на шаг 6. Иначе S1[i, j] := a, FoundAmount := FoundAmount + 1. Перейти на шаг 6.
Теперь необходимо обойти матрицу следования S1, чтобы получить массив распределения операторов по нитям:
9. Просматривая строки матрицы S1 сверху вниз находим очередную нулевую строку i. Если такая строка найдена, переходим на шаг 10, иначе – на шаг 14.
10. arThreads[i] := ThreadNum
11. Просматриваем i-ю строку матрицы S1 слева направо и находим j-й элемент строки, отличный от нуля. Если такой элемент найден, тогда переходим на шаг 12, иначе – на шаг 13.
12. i := j. Перейти на шаг 10.
13. ThreadNum := ThreadNum + 1. Перейти на шаг 9.
14. Конец алгоритма.
4.4 Алгоритм уплотнения нитей задачи.
Данные на входе алгоритма: массив распределения операторов задачи по нитям arThreads, массив поздних сроков начала выполнения операторов arLastTimes.
Результат: массив распределения операторов задачи по нитям после применения процедуры уплотнения arPackThreads
Описание алгоритма:
Алгоритм построен на планировании выполнения операторов задачи при условии, что оператор выполнится не позже своего позднего срока (наихудший случай обеспечивающий оптимальное решение).
Вспомогательные переменные:
l_dwThreadsAmount – количество нитей задачи
l_arFinishItems – массив, размерности l_dwThreadsAmount, i-й элемент которого содержит номер оператора, являющегося терминальным для i-й нити.
l_dwMatrixSize – размер матрицы следования.
l_dwRealTime – реальное время возможного начала выполнения оператора (вычисляется на основе реальных времен всех предшествующих операторов).
l_arFinishTimes – массив времен завершения выполнения операторов на i-м процессоре.
pV – время выполнения i-го оператора.
- Инициализировать массив arPackThreads элементами массива arThreads.
- Множество процессоров инициализируем пустым значением
- Определить терминальные вершины нитей и заполнить массив l_arFinishItems.
- Упорядочить операторы по поздним срокам начала их выполнения.
- Counter := 0;
- Если Counter < l_dwMatrixSize, тогда перейти на шаг 7. Иначе перейти на шаг (ДОБАВИТЬ).
- Взять элемент упорядоченного по возрастанию массива поздних сроков начала выполнения операторов с номером Counter и определить номер оператора i, соответствующий этому сроку, и номер нити j. Counter := Counter + 1;
- Вычисляем реальное время начала выполнения i-го оператора l_dwRealTime.
- Если есть активный процессор, на котором запущена нить с номером j, тогда l_arFinishTimes[j] := l_dwRealTime + pV[i]; Перейти на шаг 12. Иначе перейти на шаг 10.
- Если есть неактивный процессор, который был загружен нитью k, загружаем его операторами нити j, а в массиве arPackThreads все значения j изменяем на k. Перейти на шаг 12. Иначе перейти на шаг 11.
- Добавить новый процессор и загрузить его нитью j. Перейти на шаг 12.
- l_arFinishTimes[j] := l_dwRealTime + pV[i]; Перейти на шаг 6.
- Перенумеровать массив arPackThreads последовательно по возрастанию (чтобы не было пропусков в нумерации).
- Конец алгоритма.
4.5 Алгоритм распределения нитей по узлам вычислительной сети.
Данные на входе алгоритма: матрица следования arThreadMatrix, в которой в качестве узлов выступают уплотненные нити, а связи – связи между отдельными нитями. При этом на пересечении i-й строки и j-го столбца находится число, определяющее затраты на передачу данных от нити j к нити i. Матрица минимальных путей (полученная с использованием алгоритма Уоршела-Клини), ведущих из i-го узла в j-й узел arPaths.
Результат: массив распределения нитей по узлам вычислительной сети.
Описание алгоритма:
Так как при уплотнении нитей мы считали, что затраты на передачу данных от одной нити к другой постоянны, то считаем, что эти затраты – ни что иное, как нагрузка на магистраль связи (а не временные затраты). При этом эти затраты не зависят от количества транзитных передач между узлами. Поэтому для поиска оптимальной структуры можно использовать матрицу путей в ВС, полученную с использованием алгоритма Уоршела-Клини. Кроме того, так, как современная элементная база построена таким образом, что современный сигнальный или иной процессор имеет достаточно развитый набор периферии, что позволяет осуществлять взаимодействие с соседними модулями, практически не задействуя для этого ресурсы процессорного ядра. Поэтому считаем, что любой процессор в ВС может одновременно (практически) выполнять как вычисления, так и транзитную передачу.
Считаем что после этапа уплотнения у нас получилось dwThreadsAmount нитей.
Размер ВС считаем равным VSSize.
- CurrentSum := 0;
- MaxSum := 0;
- Выбираем из множества узлов ВС очередную выборку размером dwThreadsAmount (i1, i2, …in, …).
- Из матрицы arPaths исключем вершины, не вошедшие в выборку.
- Найти скалярное произведение двух полученных матриц и присвоить его CurrentSum.
- Если CurrentSum > MaxSum, запомнить текущую выборку как оптимальную, MaxSum := CurrentSum.
- Если еще есть непроанализированные выборки, перейти на шаг3. Иначе перейти на шаг 8.
- Присвоить результату сохраненную выборку.
- Конец алгоритма.
5 Описание интерфейса программы.
При запуске программы появляется диалог ввода входных параметров задачи (см. рис. 5.1.)
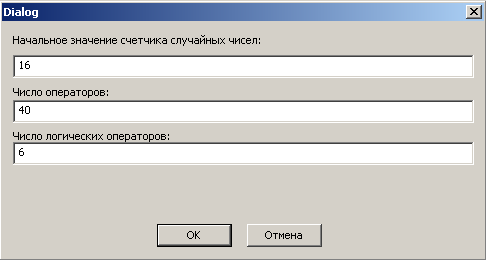
Рис. 5.1. Диалог ввода входных параметров задачи.
Здесь мы задаем размерность задачи (число операторов), начальное значение счетчика случайных чисел, которое используется при построении матрицы следования задачи и число логических операторов.
После ввода параметров программа производит полный расчет (т.е. выполняет все алгоритмы) и представляет результаты своей работы (см. рис. 5.2)
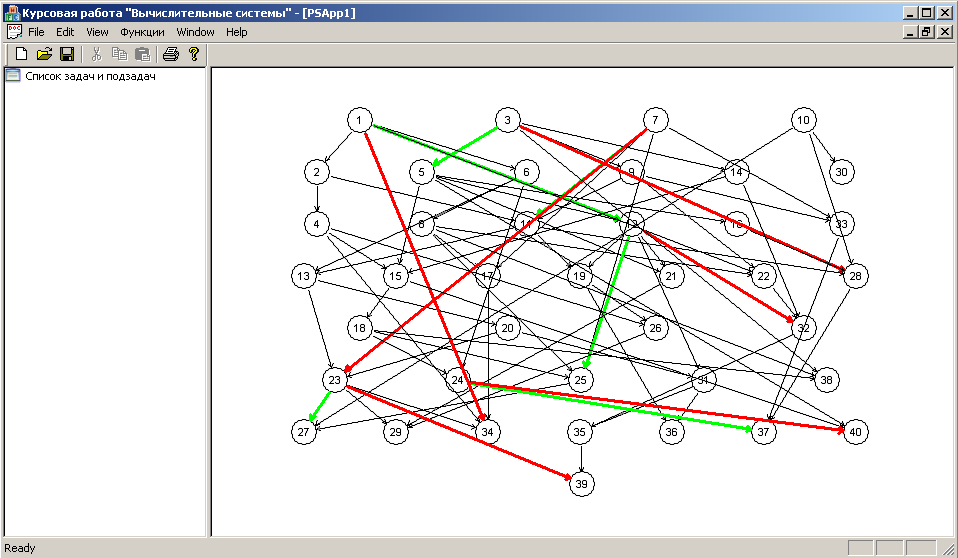
Рис. 5.2. Результат расчетов программы.
На рис 5.2. представлен граф сгенерированной задачи. При этом красными стрелками показаны логические связи при значении условного оператора Истина, а зелеными – логические связи при значении условных операторов Ложь.
Чтобы просмотреть результаты расчетов необходимо сделать двойной щелчок в левой части окна на надписи Список задач и подзадач. Результат показан на рис. 5.3.
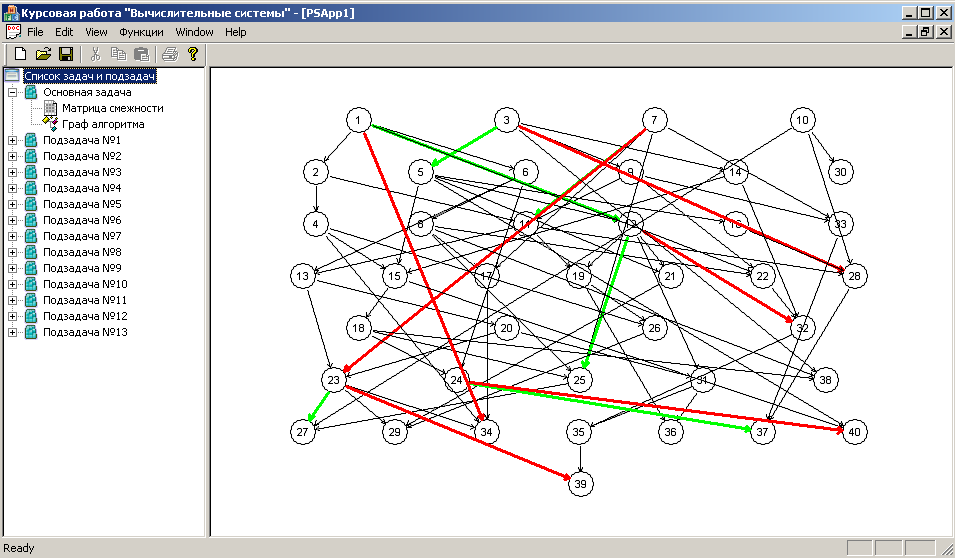
Рис. 5.3. Список подзадач задачи.
В результате раскроется список, и будет выведен список подзадач, который был получен при разбиении ИЛГ, представляющего исходную задачу, на ИГ. Как видно из рис. 5.3, из исходной задачи получилось 13 различных подзадач.
На рис 5.3. показано графическое представление задачи. Программа предоставляет также возможность табличного отображения модифицированной матрицы следования задачи (и подзадач соответственно). Для этого необходимо для задачи или соответствующей подзадачи выбрать пункт Матрица смежности. В результате в правой части окна отобразится модифицирования матрица следования задачи (или подзадачи) (см. рис. 5.4.)
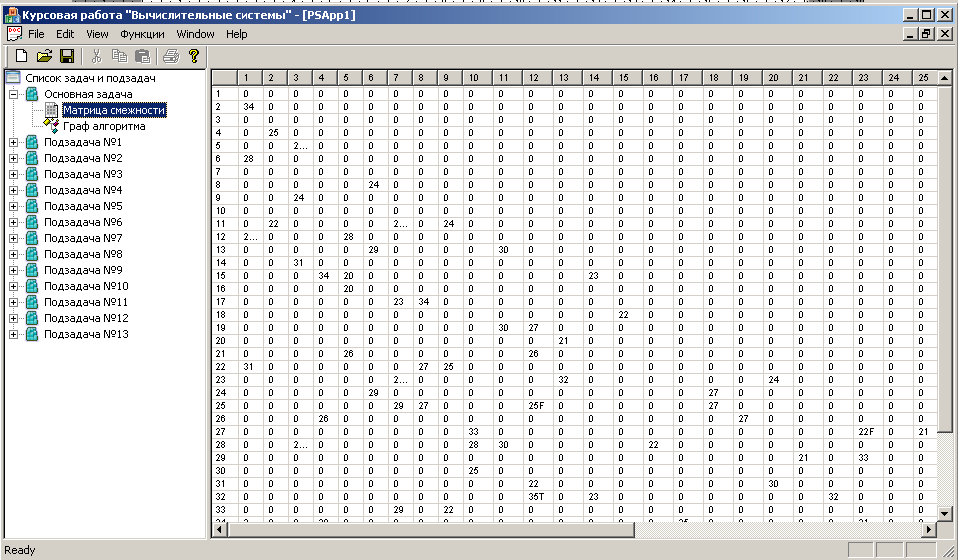
Рис. 5.4. Модифицированная матрица следования задачи.
В этой матрице, если из узла j идет связь в узел i, то на пересечении j-го столбца и i-й строки расположен ненулевой элемент. При этом величина ненулевого элемента показывает нагрузку на линии связи при осуществлении передачи параметров от оператора j к оператору i. Если j-й оператор является логическим, тогда в ячейке [i, j] рядом с отличным от нуля числом стоит буква T или F, которая определяет условие перехода.
Последний столбец в модифицированной матрице следования определяет затраты на выполнение i-го оператора.
Для того, чтобы просмотреть разбиения подзадачи на нити, необходимо выбрать для подзадачи пункт Граф алгоритма (см. рис. 5.5).
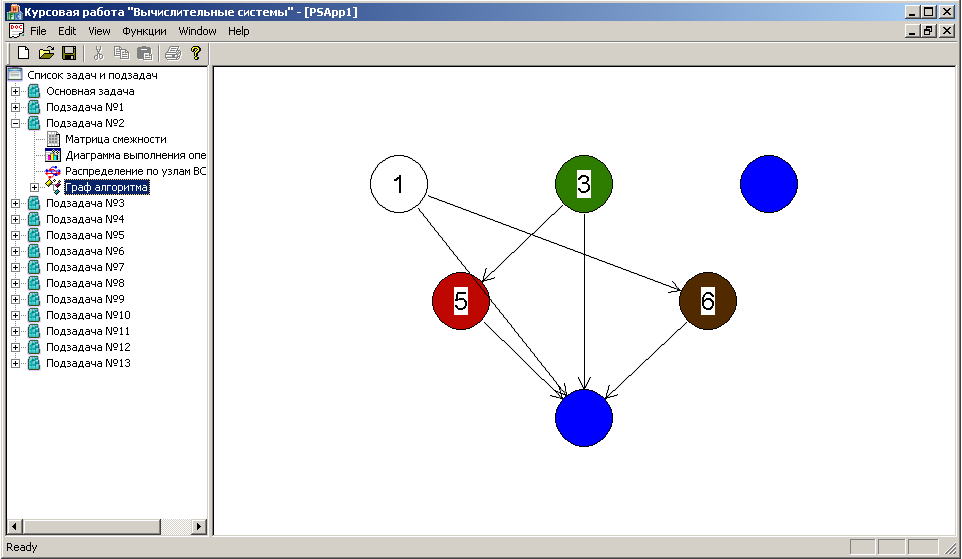
Рис.5.5. Графическое представление подзадачи с учетом разбиения на нити.
На рис. 5.5. вершины входящие в разные нити показаны разным цветом. При этом если вершина не имеет номера и имеет синий цвет, это значит, что это «комплексная» вершина, т.е. она определяет группу вершин. Для того, чтобы «развернуть комплексную вершину», необходимо полностью развернуть список Граф алгоритма.
Для отображения диаграммы запуска нитей подзадачи, необходимо выбрать пункт Диаграмма выполнения операторов (см. рис. 5.6.)
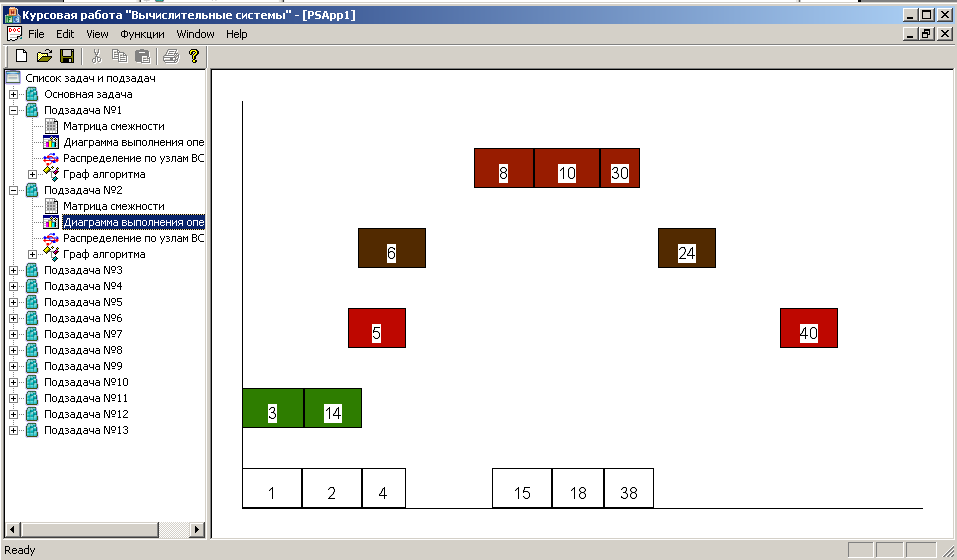
Рис. 5.6. Диаграмма выполнения операторов при разбиении подзадачи 2 на нити.
Как видно из рис. 5.6. в результате разбиения и уплотнения мы получили для подзадачи 2 пять нитей.
Чтобы отобразить распределение нитей по узлам вычислительной сети, необходимо для подзадачи выбрать пункт Распределение по узлам ВС (см. рис. 5.7).
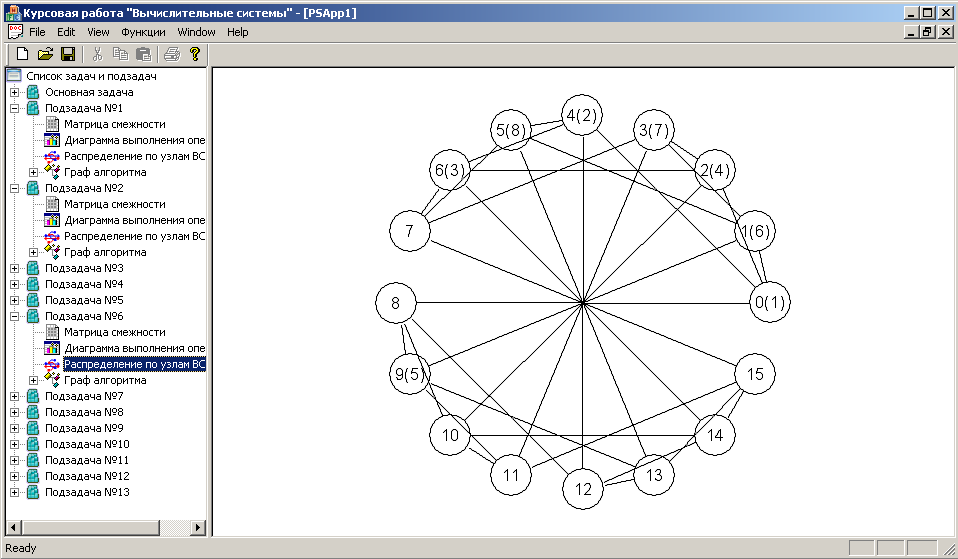
Рис. 5.7. Распределение нитей по узлам ВС.
Как видно из рис. 5.7 искомая ВС со структурой n-мерный двоичный гиперкуб должна иметь 16 узлов (т.е. n = 4). При этом наиболее оптимальное распределение нитей для 6-й подзадачи показано на рис. 5.7.
Заключение
Разработанная программа полностью соответствует техническому заданию. Она позволяет не только найти оптимальную конфигурацию вычислительной сети, но и распределение нитей по узлам ВС для каждой отдельной подзадачи.
Основным достоинством программы является ее универсальность и способность к расширяемости (с точки зрения доработки). Так для того, чтобы определить конфигурацию ВС для другой задачи надо лишь поменять входные параметры программы. Для изменения структуры ВС достаточно лишь добавить в программу новый класс с генерацией матрицы смежности этой структуры и перекомпилировать программу.
К числу недостатков следует отнести слишком большую вычислительную сложность алгоритма распределения нитей по процессорам ВС. Этот алгоритм использует полный перебор для определения оптимального решения, что является не слишким эффективным решением с точки зрения вычислительной сложности. Но все же для небольших задач время решения все равно достаточно приемлемо.
Список использованных источников
- Ю.М. Руденко Вычислительные системы: Методическме указания по выполнению курсовой работы. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 12 с.
- Ю.М. Руденко Конспект лекций по курсу “Вычислительные системы”. МГТУ, 2006г.
- X. Tang, J. Wang, K. B. Theobald, G. R. Gao Thread Partitioning and Scheduling Based on Cost Model – CAPSL Technical Memo 03 April 15, 1997
- J. N. Amaral, G. R. Gao, E. D. Kocalar, X. Tang Design and Implementation of an Efficient Thread Partitioning Algorithm – CAPSL Technical Memo 30 July 1, 1999
- rum.ru/programming/digest/gaisarian/#4
