Зазеркалье Льюиса Кэрролла. Симметричные фигуры Тип урок
| Вид материала | Урок |
- Исследовательская работа по литературе ученика 5 «Б» класса Ярчука Эрнста «Герои сказок, 195.77kb.
- Январь, 126.16kb.
- Внеклассное мероприятие по математике на тему: "В мире логики Льюиса Кэрролла", 72.43kb.
- Льюиса Кэрролла «Приключения Алисы в стране чудес», 9.29kb.
- Реферат по теме: Творчество Льюиса Кэрролла, 201.07kb.
- А в этом году исполняется 140 лет книге «Алиса в Зазеркалье». Многие поколения зачитывались, 16.45kb.
- Стране Чудес "Алиса в Стране чудес", 28.37kb.
- Урок проводится в виде познавательно-развлекательной программы для 8-х классов. Урок, 308.58kb.
- Биография Льюиса Кэрролла, 119.58kb.
- Биография Льюиса Кэрролла, 131.22kb.
Тема урока: "Путешествие в Зазеркалье Льюиса Кэрролла. Симметричные фигуры"
Тип урока: урок- игра.
Цели:
- Расширить знания учащихся о симметрии.
-Закрепить навык построения симметричных точек и фигур, относительно данной прямой.
- Развивать коммуникативные качества (умение делать выводы, высказывать свои мысли), логическое мышление, практические умения.
- Развивать наблюдательность, расширять кругозор и познавательный интерес учащихся на основе межпредметных связей.
Оборудование: карточки с заданиями, конверты с симметричными и несимметричными геометрическими фигурами, учебник «Математика» Л. Г. Петерсон, компьютер, мультимедийный проектор, презентация, отрывки из мультфильма «Алиса в Зазеркалье»,
таблицы для физкультминутки.
“Нельзя быть настоящим математиком, не будучи немного поэтом.”
Карл Вейерштрасс
- Организационный момент.
- Здравствуйте, ребята!
Сегодня у нас необычный урок, поэтому начать его я хочу словами выдающегося немецкого математика Карла Вейерштрасса: ,, Нельзя быть настоящим математиком, не будучи немного поэтом.” На уроке мы попробуем совместить, казалось бы, несовместимое - математику и литературу.
2. Основная часть.
1) Биография Льюиса Кэрролла
А поможет нам в этом ещё один математик – англичанин Чарльз Лютвидж Доджсон.
(портрет на слайде)
- Поднимите руку, кому знакомо это имя?
Тогда представлю его вам ещё раз - Льюис Кэрролл.
( тот же слайд)
- А кому знакомо это имя? Что вы о нём знаете?
Итак, мы говорим об одном и том же человеке. Труды, посвященные математике, Чарльз Доджсон подписывал своим настоящим именем, а все литературные труды – псевдонимом – Льюисом Кэрроллом.
О писателе Льюисе Кэрролле мы уже говорили на уроке внеклассного чтения, сегодня немного узнаем о жизни Чарльза Доджсона.
Чарльз с детства увлекался математикой. Он с отличием окончил Оксфордский колледж и, благодаря хорошим математическим способностям, был приглашён преподавать математику. Учителем математики он проработал более тридцати лет.
Его перу принадлежат солидные труды по математике (всего он создал шесть научных трудов), но особой виртуозности он достиг в составлении и решении сложных логических задач.
Достижения Доджсона в области математической логики намного опередили свое время. Он издал двухтомник под названием “Символическая логика” и сборник для детей “Логическая игра”.
Доктор Доджсон сделал множество изобретений. Некоторые из них были повторены годы спустя другими людьми и вошли в широкое употребление:
- он разработал стратегию игры “Пятнашки”
- изобрел шахматы для путешественников, где фигуры держались на доске с помощью маленького выступа, соответствующего углублению в клетке;
- приспособление для того, чтобы писать в темноте, которое он называл Никтографом1;
- способы проверки деления числа на 17 и 13,
- приемы для запоминания последовательного ряда цифр
- бесчисленные игрушки и сюрпризы,
- заменитель клея,
и многое, многое другое.
Но больше всего математик Чарльз любил детей. Он был одиноким человеком, без семьи. А у его друга Лиддела было трое детей. Старшую девочку звали Алиса.
Вот для нее и ее сестер Чарльз придумывал различные сказки, где героиней была, конечно же, Алиса.
Первая книга называлась «Алиса в стране чудес». Мы знакомились с ней на уроке внеклассного чтения. А вот как, по словам автора, появилась новая книга об Алисе.
- В какой руке ты держишь апельсин? – спросил я.
- В правой, - сказала Алиса.
- Теперь посмотри на ту маленькую девочку в зеркале. А она в какой руке держит апельсин?
Алиса внимательно посмотрела на свое изображение.
- В левой, - отвечала она.
- Как это объяснить? - спросил я.
Задача была не из легких, но Алиса не растерялась.
- Ну, если бы я стояла по ту сторону зеркала, - сказала она, - апельсин был бы у меня в правой руке, правда?
- Молодец, Алиса! – Лучшего ответа я ни разу не слышал!
Разговор этот дал окончательное направление моим мыслям о новой книжке. Я назвал ее «Сквозь зеркало и что там увидела Алиса».
2) Актуализация знаний о симметрии
В зеркале все становится наоборот: правая рука превращается в левую, левая нога - в правую.
Ежедневно каждый из нас по несколько раз видит свое отражение в зеркале. Это настолько обычно, что мы не удивляемся, не задаем вопросов, не делаем открытий. С помощью зеркала мы прикасаемся к удивительному математическому явлению – симметрии. С понятием симметрии мы познакомились вчера на уроке.
- Что такое симметрия? (Симметрия – это одинаковость в расположении частей чего-либо по противоположным сторонам от точки, прямой или плоскости.)
Посмотрите на снежинку, бабочку, листок. Что объединяет эти рисунки? (Их объединяет то, что они симметричны.)
Если разделить пополам снежинку, бабочку, листок, приставить зеркало и посмотреть на зеркало сбоку, то мы увидим прямую, а отображенная в зеркале половинка фигуры дополнит ее до целой.
– Как назвать прямую, поделившую наши фигуры на две равные части? (Ось симметрии)
- Что произойдёт, если симметричную фигуру сложить пополам по оси симметрии? (Ее части совпадут)
- Как называют такие фигуры? (Симметричные фигуры)
Если рисуют зеркальное отражение предметов, используя линию, к которой приставлено зеркало, то говорят, что эти предметы симметричны относительно этой линии. А такие фигуры называют симметричными.
- Какую симметрию мы изучаем? (Осевую симметрию.)
С явлениями симметрии, с симметричными фигурами мы встречаемся буквально на каждом шагу. Нельзя не восхищаться порхающей бабочкой, ярким цветком, загадочной снежинкой. Об этих и других предметах можно сказать, что они красивы.
В древности слово «симметрия» употреблялось в значении «гармония», «красота».
И в основе их красоты лежит симметрия. Но симметрия – это не только красота. Симметричность фигуры необходима рыбе, чтобы плавать, птице, чтобы летать.
Симметрия есть и в творениях природы (животные, растении, кристаллы…) и в творениях человеческих рук (дома, автомобили, самолеты, мебель, посуда…).
Сегодня на уроке мы закрепим наши знания о симметрии, научимся строить симметричные фигуры, будем решать интересные примеры и задачки.
3) Путешествие по Зазеркалью.
Фрагмент мультфильма 1. « Ой, как бы мне хотелось попасть в Зазеркалье… А давай играть, будто мы туда сможем пройти»
- А вы бы хотели вместе с Алисой попасть в Зазеркалье? Для этого необходимо правильно выполнить задания.
Активизация (массаж) биологически активных точек.
Посмотрите на печатные буквы. Некоторые из них тоже имеют оси симметрии.
Вертикальная ось симметрии: П, Т, Ш.
Горизонтальная ось симметрии: К, З, Э
Есть буквы, у которых две оси симметрии: Х, Ж, Н.
У некоторых букв нет оси симметрии: Ч, Б, Г.
Чтобы попасть в Зазеркалье найдите оси симметрии у букв, составляющих имя девочки.
(Работа в карточках, на которых написано имя АЛИСА)
Проверка выполнения задания. (взаимопроверка )
Фрагмент 2. «Тут Алиса сама оказалась на каминной полке, хотя сама не заметила, как она туда попала…»
Симметрию можно увидеть и в целых словах, которые читаются одинаково как слева направо, так и справа налево: ПОТОП, ТОПОТ, ШАЛАШ.
Встречаются и целые фразы, которые обладают такими свойствами, если не считать пробелы между словами.
ИСКАТЬ ТАКСИ
АРГЕНТИНА МАНИТ НЕГРА
Такие слова и фразы называются ПАЛИНДРОМАМИ
Фрагмент 3. «Что это я здесь сижу? Мне надо торопиться, а то я не успею осмотреть всё, что здесь есть…»
- В кого превратился котёнок в Зазеркалье? (В чёрную королеву)
Фрагмент 4. «Навстречу Алисе шла настоящая чёрная королева»
Но Алиса никак не могла с ней встретиться. Поможем ей. Для этого необходимо выполнить следующее задание.
- Какие точки являются симметричными? (Симметричные точки расположены на прямой, перпендикулярной оси симметрии, на равном расстоянии от неё.)
- Выдели цветом симметричные точки.
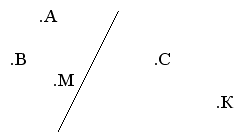
- Назовите, какие точки вы выделили. Почему?
Молодцы, вы помогли Алисе встретиться с королевой.
Фрагмент 5. «- По-моему, Зазеркалье страшно похоже на шахматную доску… А мне бы хотелось, чтобы меня приняли в эту игру хотя бы пешкой. Хотя больше всего мне хотелось быть королевой.
- Это легко устроить. Становись белой королевской пешкой. Ты сейчас стоишь на второй линии. Доберёшься до восьмой – станешь королевой.»
Итак, отправляемся с Алисой в путь по шахматной доске и знакомимся с правилами игры.
Фрагмент 6. « Пешка, как ты знаешь, первым ходом может прыгнуть через клетку. Так что третью клетку ты проскочишь на всех парах на паровозе »
(кадр Алиса в поезде, идёт кондуктор) «Надеюсь, вы понимаете, что значит думать хором, потому что мне это неясно»
Мы умеем хором отвечать.
«Зеркальная разминка»
1) Одно число очень любило любоваться своим отражением в зеркале. Мимо проходила Алиса и увидела в зеркале число 18. Какое число смотрелось в зеркало? (Ответ: 81).
2) У крылечка протекала речка.
Отражались в речке той:
Дед с седою бородой,
Внук - мальчишка озорной,
Бабушка с лукошком,
Пес и рыженькая кошка.
Сколько в водичке
Отражалось лисичек?
Ответ: 0
3) Отгадайте-ка, ребятки,
Что за цифра-акробатка?
Если на голову встанет,
Ровно на три больше станет?
Ответ: цифра 6.
Мы на 4 линии (Кадр поезд перелетает через клетку)
Фрагмент 7. «На четвёртой ты встретишь Труляля и Траляля»
- Почему у них такие имена?
Физминутка
Будь зеркальным отраженьем,
Повторяй мои движенья:
Фрагмент 8. «Задом наперёд совсем наоборот»
(Выполняют за учителем движения под первый куплет песенки Труляля и Траляля)
Фрагмент 9. «Пятая клетка залита водой»
Поможем Алисе переплыть её.
Чтобы Алисе благополучно миновать пятую клетку, выполним задание. (Учебник стр. 47, №3)
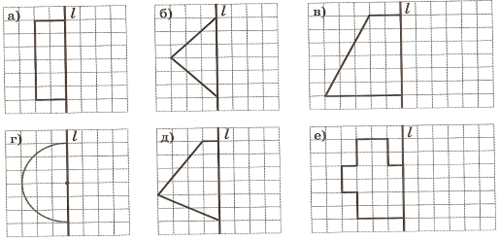
Каждый ученик берёт карточку с практической работой, на которой нужно дорисовать симметричные фигуры и самостоятельно выполняет задание.
Взаимопроверка работ учащимися.
Фрагмент 9-а. (кадр Алиса плывёт на лодке)
Молодцы, вы помогли Алисе. Двигаемся дальше.
Фрагмент 10. «В шестой расположился Шалтай-Болтай»
- Как Алиса поняла, что перед ней Шалтай-Болтай? /Написано на лбу./
- На что указывает его имя? /«…на ту хрупкую форму, которая мне присуща»./
Фрагмент 11. ( звучит песенка «Шалтай-Болтай сидел на стене…»
Следующий кадр: королевское войско, встреча с королём)
«Милая, ты там никого не встречала? Я же послал туда всю свою конницу, всю свою рарь.
- Их там целые тысячи…
- Точнее четыре тысячи двести семь человек»
Выполним задание белого короля.
Представьте число 4207 в виде суммы разрядных слагаемых, в виде различных единиц счёта, в виде различных единиц измерения.
4207 = 4000 + 200 + 7
4207ед = 420д 7ед = 42с 7ед =4т 207ед
4207мм = 420см 7мм =42дм 7мм = 4м 207мм
Фрагмент 12 «Взгляни на дорогу. Кого ты там видишь?
- Никого.
- Мне бы такое зрение. Видеть никого да ещё на таком расстоянии»
(Упражнения для глаз)
Фрагмент 13. «Единорог и лев ведут бой за мою корону. Побежали посмотрим…
Перерыв 10 минут.
- Это что такое?
- Это живой детёныш.
- А я думал, что дети – это сказочные чудовища. Угости нас пирогом, чудище…»
- Что особенного было в зазеркальных пирогах? (Их сначала надо раздать, а затем разрезать.)
Разделим пироги разной геометрической формы.
-Перед вами геометрические фигуры.
-Найдите оси симметрии в пирогах, имеющих различную геометрическую форму.
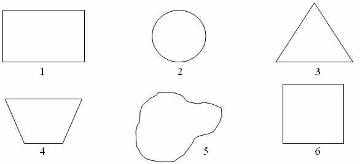
- Сколько же всего осей симметрии у пирога прямоугольной формы? ( Две)
-Сколько осей симметрии вы нашли у круглого пирога? ( Много)
- У пирога треугольной формы? ( Три)
Какой формы пирог под номером 4. Сколько провели осей симметрии? ( Одну)
- Сколько осей симметрии у пирога под номером 5? ( Нет осей)
- Сколько их у пирога квадратной формы? ( Четыре)
Вывод:
Некоторые фигуры имеют несколько осей симметрии. У некоторых фигур оси симметрии нет.
- Как назовём такие фигуры?
Справились с заданием. Отправляемся дальше.
Фрагмент 15 « Седьмая клетка заросла лесом, но рыцарь на коне проведёт тебя через него»
( Алиса идёт по лесу, появляется чёрный рыцарь)
Фрагмент 16. «Остановись. Я взял тебя в плен»
Поможем белому рыцарю освободить Алису.
Как узнать – симметричны ли данные фигуры относительно проведённой прямой?
(Для этого необходимо определить, одинаковая ли у них форма, размер, одинаково ли удалены точки от оси симметрии, лежат ли все точки на перпендикулярной прямой.)

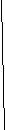
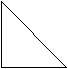

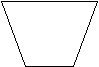


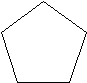




Рыцарь проводит Алису через лес, но надо помочь ему удержаться в седле.
Фрагмент 17. «Великое искусство верховой езды заключается в том, чтобы удержать равновесие. Мой ум работает, не переставая. Чем ниже голова, тем глубже мысли»
Задание
Является ли проведенная прямая осью симметрии фигуры? Почему?
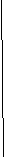


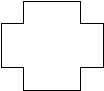

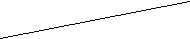
Проверка.
Фрагмент 19 «Вон твоя последняя линия. Теперь я покину тебя, дитя моё»
«На восьмой линии мы встретимся как равные. Ты станешь королевой»
Чтобы добраться до восьмой линии, выполним задание.
Выполните вычисления в столбик на карточках. Найдите в таблице ответы и поставьте соответствующую букву. Вы угадаете зашифрованное слово. (Задание на карточке)
Фрагмент 20 «( Алиса перелетает на восьмую линию, превращается в королеву)
Я и не думала, что так скоро стану королевой»
3. Подведение итогов. Рефлексия.
– В какой стране мы путешествовали?
– Мы были в сказке, а нужна ли симметрия в жизни?
На уроке
Я повторил…
Я запомнил…
Мне понравилось…
Я хочу…
4. Домашняя работа. (Карточки для домашней работы)
