Секция 9 Ю. И. Нечаев, Д. Г. Тихонов

Вид материала

Документы

Содержание 1. Постановка задачи 2. Климатические спектры волнения 3. Нечеткая формальная система 4. Реализация нейросетевых ансамблей 5. Практическое приложение разработанной системы

Подобный материал:

• Xix всероссийская конференция, 249.97kb.
• Российский Университет Дружбы Народов Кафедра математических методов анализа экономики, 17.48kb.
• 1 ноября в с. Табуны прошёл ежегодный молодёжный фестиваль «Табуния-2008». Внём приняли, 111.28kb.
• Российская академия наук центр цивилизационных и региональных исследований в. Д. Нечаев, 1680.34kb.
• Научные направления и секции конференции: Секция, 39.35kb.
• Научная программа Секция Порядок и беспорядок в минералах. Председатели: М. И. Новгородова, 47.17kb.
• Александров Б. П., Тихонов В. Н., Троицкий С. К. Рыбохозяйственное значение Аксайско-Донского, 31.9kb.
• Конкурс на лучшее решение бизнес-кейсов. Секция Мировая экономика и инвестиции Секция, 139.21kb.
• Темы секционных заседаний: Секция «Австрия в мировой истории». Секция «Австрийская, 54.73kb.
• Фаддеев Д. К., Соминский И. С. Задачи по высшей алгебре, 765.88kb.

Ю.И. НЕЧАЕВ, Д.Г. ТИХОНОВ

Государственный морской технический университет, Санкт-Петербург

int@csa.ru


НЕЙРОПРОГНОЗ НА ОСНОВЕ ЛОГИЧЕСКОГО ВЫВОДА

ПО ПРЕЦЕДЕНТАМ


Аннотация

Обсуждается подход к построению нейросетевых ансамблей в задаче прогнозирования параметров морской среды. Анализ проведен на основе экспериментальных данных о климатических спектрах морского волнения. Разработаные ансамбли позволяют решать задачи оценки и прогноза динамики взаимодействия судна с внешней средой в бортовых интеллектуальных системах реального времени.


1. Постановка задачи


Оценка и прогноз параметров морского волнения – одна из сложных и ответственных операций при функционировании бортовых интеллектуальных систем (ИС). Надежность такой операции обеспечивается на основе сравнительного анализа данных, полученных в рамках принципа конкуренции с помощью стандартных и нейросетевых алгоритмов.

Логический вывод, обеспечивающий выбор предпочтительного алгоритма решения, осуществляется в мультипроцессорной вычислительной среде. Построение стандартных и нейросетевых моделей анализа и прогноза ведется на основе представления о климатических спектрах морского волнения. Многозначность интерпретации климатических спектров приводит к необходимости использования различных моделей нечеткого вывода [1] – [10]. Наряду с традиционными моделями практический интерес представляют модели вывода по прецедентам на основе искусственных нейронных сетей (ИНС). Формирование ансамбля нейронных сетей, обеспечивающего реализацию процедуры нечеткого вывода, осуществляется в зависимости от интегральных характеристик, описывающих закономерности динамики ветроволновых систем.

Вывод по прецедентам – достаточно часто распространенная процедура логического вывода в системах интеллектуальной поддержки принятия решений. Среди имеющихся предложений наибольший интерес представляют структуры вывода, предложенные в работах [5] и [4]. Принципиальная возможность реализации нечеткого нейросетевого вывода по прецеденту была продемонстрирована при разработке телемедицинской системы [3].

Обобщенная модель нечеткого вывода по прецедентам, объединяющая модели вывода по аналогии и экспертных рассуждениях, может быть описана в следующем виде:

М вп = Р_B, М(W),M(V), М(W,V), М_FD>, (1)

где S_РB – система нейросетевого представления базы прецедентов; М_СР – модели нечеткого вывода по прецедентам на разных уровнях иерархии решения задач анализа и прогноза процессов волнения М(W) и ветра М(V); М_WV – комплексная модель нечеткого вывода по прецедентам для совокупности процессов волнения и ветра; М_FD – модель анализа альтернатив и формирователя решений по прецедентам.

Настоящее исследование направлено на решение задач создания нейросетевой базы прецедентов, характеризующих ветроволновые поля при различном уровне возмущений, а также на формирование структуры нечеткого логического вывода по прецеденту на базе нейросетевых технологий в рамках принципа конкуренции.

Механизм нечеткого вывода предполагает использование методов и моделей, основанных на преобразовании измерительной информации в мультипроцессорной вычислительной среде (рис.1).





Рис. 1. Поток информации в задаче формирования модели нечеткого вывода по прецеденту (А) в мультипроцессорной вычислительной среде (В): NNA – нейросетевые ансамбли; КВР – база знаний прецедентов; МСР – блок моделирования и сравнительного анализа прецедентов; MS – измерительная система; СТ – конкурирующие технологии; АА – анализ альтернатив; Ф1(×), …, Ф(×a ) – данные измерений, подаваемые на стандартный (SA) и нейросетевой (ANN) алгоритмы; a₁b₁, …, a_N b_N – выходные данные для SA и ANN; F₁(×), …, F_N(×) – ситуации, определяемые в результате анализа альтернатив

2. Климатические спектры волнения


Понятие «климатические спектры» волнения введено официально на 18 Ассамблее ИМО (Intergоverment Maritime Organization, London) в 1993 году вместе с понятием «волновой климат». С помощью этих понятий открываются возможности более детального, по сравнению с существующей практикой, описания особенностей волновой погоды в конкретных районах океана. Для моделирования погодных сценариев предложен подход к типизации спектров волнения в частотном диапазоне по генетическому набору образцов так, чтобы в каждом типе спектры были геометрически подобны и различались только параметрами, соответствующими различным условиям волнообразования [9]. Суть типизации лежит в отнесении записей волновой ординаты (t) к типам зыби, ветрового или смешанного волнения. Таким образом, генетическая классификация спектральных плотностей волнения сводится к типизации по усеченным или полным моментам спектра и связанным с ними величинам. В этом случае любую спектральную плотность S(), которая при таком осреднении является случайной функцией,можно представить в виде неслучайной функции S(,) с набором случайных параметров .

Процедура классификации генетически подобных спектров, описанная в работе [9], позволяет на основании натурных данных и модельных расчетов провести идентификацию частотно-направленных спектров волнения, которые представляются в виде выражения

, . (2)

Здесь m₀₀ – нулевой момент спектра (дисперсия взволнованной поверхности), _p – весовой вклад каждой волновой системы в общую энергию, _max – частоты пиков спектра и _max – соответствующие ему направления для каждой из волновых систем.

Такой подход позволяет типизировать каждую волновую систему при помощи пяти параметров {_i, _maxi, _maxi, n, m} (здесь n, m – параметры формы спектра).

На рис. 2 приведен пример классификации частотно-направленных спектров для Баренцева моря. Здесь выделено 6 классов (ветровое волнение I-1, зыбь I-2, смешанное волнение II-1,2,3, сложная картина волнообразования, состоящая более, чем из двух волновых систем III).

А	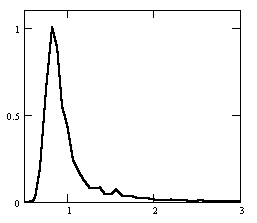B	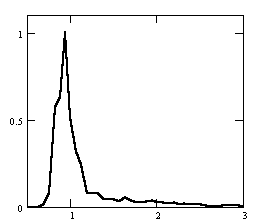C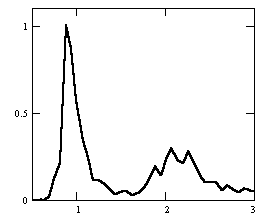
D	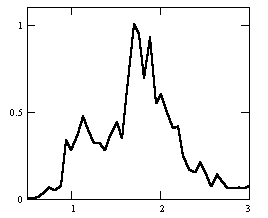E	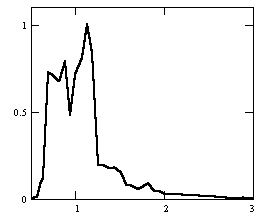F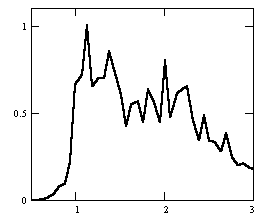

Рис. 1. Типовые нормированные спектры морского волнения: A – зыбь; B – ветровое волнение; C – смешанное волнение с разделением систем и преобладанием зыби; D – смешанное волнение с разделением систем и преобладанием ветрового волнения; E – смешанное волнение без разделения систем с преобладанием зыби; F – смешанное волнение без разделения систем с преобладанием ветрового волнения. Градуировка на графиках спектральной плотности S()/S_max по вертикальной оси;  с^-1 по горизонтальной оси


3. Нечеткая формальная система


Преобразование информации при построении нечеткой формальной системы, обеспечивающей принятие решений при выборе альтернатив A_i (i = 1, …, n), сводится к рассмотрению множество векторов, характеризующих конкретную альтернативу (ситуацию):

Rⁿ : K = (x₁,…, x_n) Rⁿ, (3)

где x₁, …, х_n – признаки, выделенные в процессе анализа априорной информации.

Исходную ситуацию характеризует матрица состояний [2] (морфологическая матрица), образуемая множеством альтернатив {A_i} и множеством признаков x_ji^p (i = 1, …, n; j = 1, …, m; p = 1, …, k). Эта матрица перестраивается и преобразуется в безразмерное пространство (матрицу стратегических решений):

. (4)

Элементы полученной матрицы представляют собой сценарии ситуаций, определяемые особенностями ветроволнового режима. Таким образом, исходная информация о динамике ветроволновых полей может быть представлена структурой ({А}, {х}), определяемой пространство принятия решений.

Практическая реализация состояний динамической системы, описывающей ветроволновые возмущения различной интенсивности, достигается на основе представления структур ({А},{х}), в виде нечеткой системы. Такая система учитывает динамику изменения предметной области (развитие и затухание шторма) и представляется в виде матрицы переходов, строками которой являются пары

(S_i, i,S_j>; i = 1, …, n; j = 1, …, m), (5)

где S_i – расширенная нечеткая формальная система; i,S_j> – пара, задающая максиминную операцию, используемую в основе композиционного правила вывода (обобщенный modus ponens); T_i – оператор минимума (Т-норма); Sj – оператор максимума (Т –конорма).

Пересечение строки S_k и столбца S_p матрицы переходов обозначается символом «Х» и указывает на возможность выполнения максиминной операции, определяемой парой i,S_j>. Эта операция сменяется на максиминную операцию, заданную парой m,S_n>.


4. Реализация нейросетевых ансамблей


Представление прецедентов осуществляется с использованием подхода, основанного на теории динамической памяти [10]. В соответствии с базовым положением этой теории рассуждения основаны на использовании структур, фиксирующих отдельные случаи (прецеденты) решения конкретных задач.

Формализация знаний о предметной области, связанной с моделированием климатических спектров волнения в форме прецедентов, осуществлена с использованием динамических структур данных. В зависимости от характера волнообразования эти структуры отражают цели, условия и последствия решения задач анализа и прогноза на различных уровнях абстракции.

База прецедентов (КВР) применительно к рассматриваемой задаче представляет собой набор нейросетевых ансамблей, характеризующих различные описания ветроволнового режима. Формально такая структура может быть представлена в следующем виде:

КPB(ANN) = ;

P(W) = {S(W), Q(W)}; P(V) = {S(V), Q(V)}, (6)

где Р(W), P(V) – прецеденты различного уровня абстракции; S(W), S(V) – ситуации (структуры), описывающие спектральный состав ветроволновых полей; C(W), С(V) – сценарии развития волнения под воздействием ветра, U(W, V) – управляющие структуры, Q – связи между прецедентами P(W) и Р(V), задаваемые дискриминационными сетями. Ситуации S(W) и S(V) – структуры данных, содержащие описание особенностей возникновения и развития ветроволновых режимов и решаемых задач (операций анализа и прогноза параметров ветра и волнения). Сценарии С(W) и C(V) задают последовательности развития ситуаций и условия их реализации в соответствии с исходными данными динамических измерений. Управляющие элементы U(W, V) в зависимости от целей и условий решения задач обеспечивают структуризацию ситуаций с учетом фактора времени и поддерживают динамическое формирование сценариев.

Настройка нейронной сети для решения задачи оценки и прогноза состояния динамической системы, определяющей конкретный прецедент (ветроволновое возмущение), предполагает выполнение этапов структурной и параметрической адаптации. В процессе структурной адаптации устанавливается оптимальная структура ИНС, а при параметрической – матрица синаптических связей. Структурный и параметрический синтез нейронной сети осуществляется на основе информации в виде обучающей и контрольной выборок. Формальная постановка этой задачи имеет следующий вид:

(NET)opt = arg _uU min Q;

U = FH, fF, hH, (NET)opt  U, (7)

где NETopt – искомая нейросеть; Q – показатель качества; U – пространство адаптации F – структурное пространство; H – параметрическое пространство;  – операция декартового произведения.

При проведении структурной адаптации учитывается, что ИНС реализует принцип эвристической самоорганизации. Этот принцип предполагает существование оптимальной нейросетевой структуры (NET)opt, обеспечивающей заданное значение критерия качества Q.


5. Практическое приложение разработанной системы


Логический вывод по прецеденту в рамках принципа конкуренции (рис. 1) в бортовых ИС представляет собой циклический и интегрированный процесс решения задачи выбора и построения структуры математического описания ветроволнового режима. Такой выбор осуществляется с использованием стратегий нечеткого вывода с использованием ИНС в мультипроцессорной вычислительной среде [6]. Окончательным решением задачи вывода является не только конкретное описание волнового поля, но и построение картины ветроволнового режима в заданном районе мирового океана. Для иллюстрации на рис. 3 представлены изолинии, характеризующие модуль погоды, сформированный по результатам вывода в бортовой ИС анализа и прогноза динамики ветроволновых возмущений.





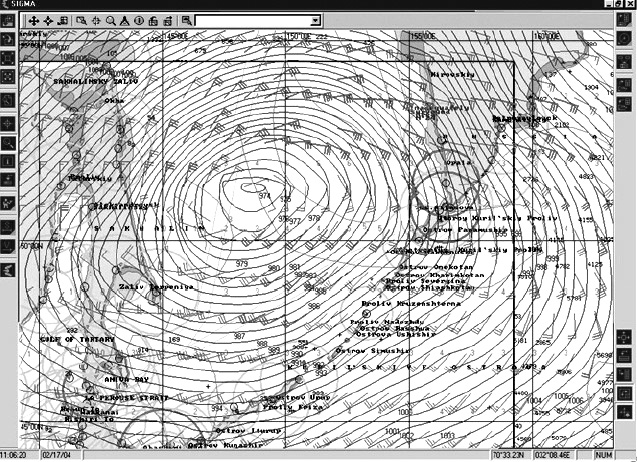
Рис. 3. Фрагмент модуля погоды, формируемый в бортовой ИС на основе функционирования механизма логического вывода по прецеденту с использованием встроенной процедуры математического моделирования

Заключение


Разработанная нейросетевая технология анализа и прогноза динамики ветроволновых полей позволяет повысить эффективность функционирования бортовой ИС обеспечения безопасности мореплавания. Реализация механизма нечеткого вывода может быть осуществлена в рамках принципа конкуренции в мультипроцессорной вычислительной среде. В сложных ситуациях используются процедуры, основанные на анализе прецедентов. При построении этих процедур находят применение модели нечеткого вывода по аналогии и ИНС-прецедентов. Нечеткий вывод по аналогии может быть построен на основе подхода [1], в котором предложено расширение стандартного правила вывода по аналогии [8] для случая, когда экспертная информация является нечеткой. Практическая реализация рассмотренной модели нечеткого вывода по аналогии осуществляется с использованием одной из операций импликации, приведенных в работе [1]. Нечеткий логический вывод на основе ИНС-прецедентов реализуется путем расширения схемы, описанной в работе [4].


Список литературы


1. Бернштейн Л.С., Боженюк А.В. Принятие решений на основе нечеткого вывода пo аналогии // Труды национальной конференции по искусственному интеллекту КИИ-2000. Переславль-Залесский. 2000. Т.2. С. 456-463.

2. Бухановский А.В., Дегтярев А.Б., Иванов С.В., Кирюхин И.А., Нечаев Ю.И., Саськов К.Г. Телемедицинский комплекс на базе суперкомпьютерных технологий // Труды Всероссийской научно-технической конференции «Телематика-2003». 3-6 июня 2003. М.: ГосНИИ ИТ «Информиика». Т. 1. С. 288-289.

3. Головина Е.Ю. Интегрированное инструментальное средство для создания нечетких динамических систем поддержки принятия решений // Труды 7-й национальной конференции по исскусственному интеллекту с международным участием КИИ-2000. Т. 2. С. 448-456.

4. Жернаков С.В. Базы знаний прецедентов активных экспертных систем на основе ансамблиевых нейросетей // Труды 4-й всероссийской конференции «Нейроинформатика-2002». Ч. 2. М.: МИФИ, 2002. С. 69-80.

5. Котенко И.В. Модели вывода по прецедентам для реализации интеллектуальных систем // Труды 6-й национальной конференции по искусственному интеллекту с международным участием КИИ-98. Пущино. 1998. Т. 1. С. 270-277.

6. Нечаев Ю.И. Нейросетевые технологии в интеллектуальных системах реального времени // Нейроинформатика-2002. Лекции по нейроинформатике. Ч. 1. М.: МИФИ, 2002. С. 114-163.

7. Нечаев Ю.И., Тихонов Д.Г. Нейросетевой алгоритм идентификации и прогноза параметров внешней среды в интеллектуальных системах реального времени // Сб. научн. тр. «Нейроинформатика-2002». Ч. 2. М.: МИФИ. С. 98-105.

8. Пойа Дж. Математика и правдоподобные рассуждения. М.: Наука, 1975.

9. Lopatoukhin L.J., Rozhkov V.A., Ryabinin V.E., Swail V.R., Boukhanovsky A.V., Degtyarev A.B. Estimation of extreme wave heights. JCOMM Technical Report, WMO/TD. № 1041. 2000.

10. Shank R.S., Abelson R. Scripts, plans, goals and understanding. – New York Lawrence Erlbaum Press, 1977.

УДК 004.032.26(06) Нейронные сети