Geum.ru

Програма курсу та методичні вказівки до виконання контрольної роботи для студентів спеціальності „Автомобілі та автомобільне господарство

Вид материалаДокументы

Содержание


Статистичний сигнал           Дні
Діаграма Парето
Діаграми кореляції
Групування даних
8. Фондоозброєність одного працівника по активній частині основних фондів(х
Подобный материал:
1   2   3   4   5

Виручка


Верхня контрольна границя +3

+2

+ 

Середня лінія



-  

-2   

-3  

Нижня контрольна границя -3 

Статистичний сигнал

         Дні


1 2 3 4 5 6 7 8 9 10 11


Рис.7. Приклад контрольної карти Шухарта


Слід зазначити, що середнє значення може бути розраховане тільки для стабільної системи за відсутності спеціального чинника. При цьому використовують не менше, ніж 25, краще 100 значень. У деяких випадках при вивченні процесів, які мають місце в системах обслуговування, зробити це важко, а іноді і неможливо, тому що кожна послуга може мати свої особливі риси, які не оцінюються однаковими значеннями контрольованого параметру. Також достатньої для статистичного аналізу сукупності абсолютно однакових послуг може просто не існувати.

Разом з тим, досвід показує, що всі ці правила не завжди дають правильну відповідь. Це викликано, перш за все, тим фактом, що реально в природі не існують абсолютно стабільні системи. Таке поняття вводиться як математична абстракція, яка з певною точністю може допомогти розв’язати практичну задачу. Також не можна визначити природу спеціальних чинників. В кінці кінців, у разі знищення всіх чинників, які за цією методологією можна називати спеціальними, залишаються звичайні чинники, які теж сприяють наявності варіацій в системі. І далі для покращення показників стабільної системи найбільш суттєві із звичайних чинників виявляються і їх дія нейтралізується, що приводить до зменшення варіацій в системі і покращення якості результату її роботи.


Існують три основні типи контрольних карт:
  1. Контрольні карти Шухарта.
  2. Контрольні карти приймального контролю.
  3. Адаптивні контрольні карти.

В залежності від кількості врахованих вибіркових спостережень контрольні карти поділяються на :
  • Контрольні карти з пам’яттю (контрольні карти кумулятивних сум CUSUM, контрольні карти експоненційно зважених ковзних середніх EWMA, контрольні карти ковзних середніх та ковзних розмахів, контрольні карти трендів);
  • Контрольні карти без пам’яті (контрольні карти Шухарта).

Контрольні карти класифікують в залежності від типу статистичних показників та сфери використання .

Контрольні карти Шухарта залежно від типу статистичних показників поділяють на такі види:

1. Контрольні карти для кількісних ознак даних:
  • Контрольна карта середніх значень 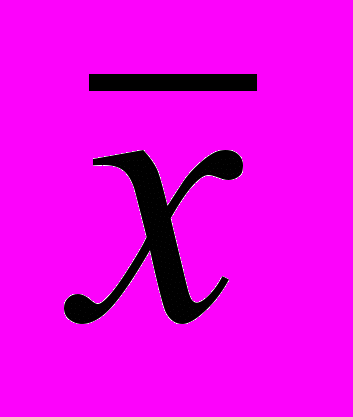і розмахів варіації R:

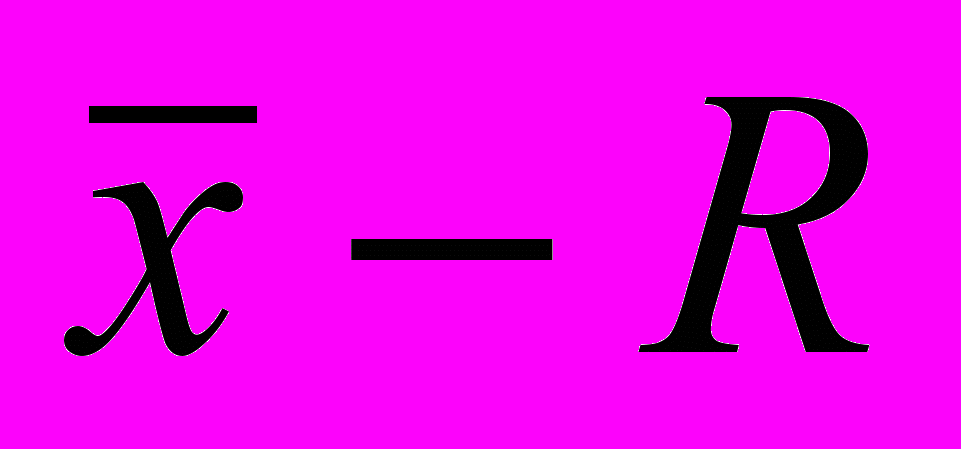()– карти ;
  • Контрольна карта середніх значень 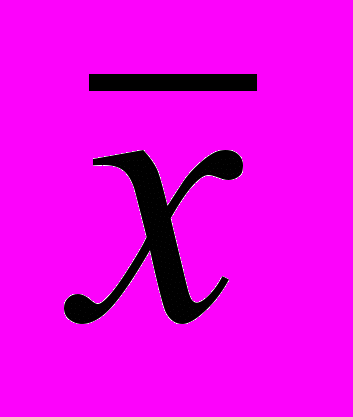і середньоквадратичних відхилень S: (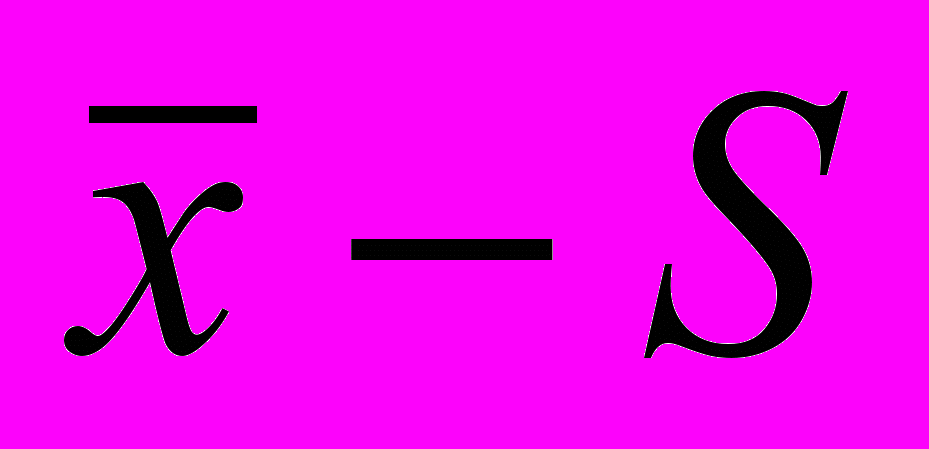) – карти;
  • Контрольна карта медіан 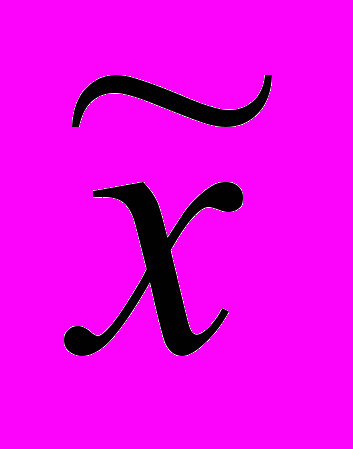і розмахів варіації R: (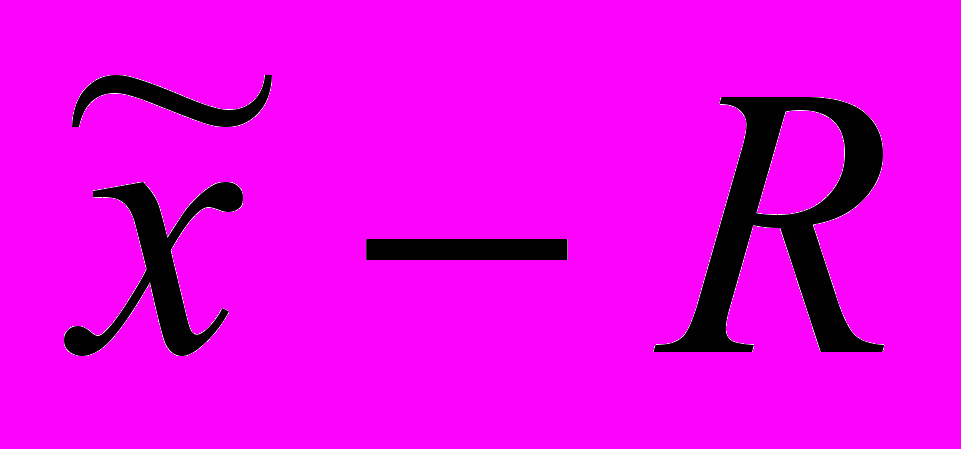) – карти;
  • Контрольна карта індивідуальних спостережень х та ковзних розмахів MR: (х – MR) – карти.

2. Контрольні карти для альтернативних ознак даних:
  • Контрольна карта часток невідповідностей, дефектів (р – карта);
  • Контрольна карта кількості дефектів, дефектних виробів (np – карта);
  • Контрольна карта кількості невідповідностей на одиницю продукції

(с – карта );
  • Контрольна карта середньої кількості невідповідностей на одиницю продукції (u – карта).

До найпоширеніших приймальних контрольних карт належать:
  • приймальні контрольні карти середніх значень 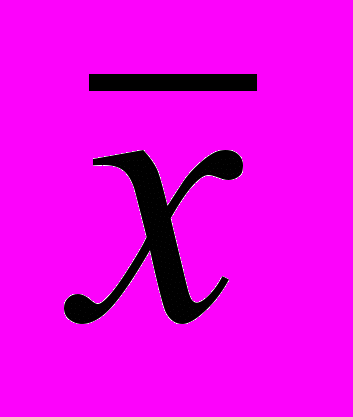і розмахів варіацій R;
  • приймальна контрольна карта часток невідповідностей продукції р;
  • приймальна контрольна карта кількості дефектів с.

У залежності від мети використання існують наступні види контрольних карт:
    • Контрольна карта для регулювання технологічних процесів;
    • Контрольна карта для аналізу технологічних процесів.

Контрольні карти в залежності від виду врахування в часі результатів спостережень за перебігом процесу поділяються на два види:
      1. Одновимірні контрольні карти;
      2. Багатовимірні контрольні карти .

До багатовимірних контрольних карт (контрольні карти багатовимірного статистичного контролю якості процесів), які враховують попередні результати спостережень за перебігом процесу, належать :
        • багатовимірна контрольна карта Шухарта (χ2 –карта);
        • Т2 – контрольна карта Хотеллінга;
        • Контрольна карти багатовимірного експоненційно зваженого ковзного середнього (MEWMA);
        • Контрольна карта кумулятивних сум (MCUSUM) .

χ2 – карта , Т2 – контрольна карта Хотеллінга використовують інформацію, яка базується на останніх спостереженнях, тільки з однієї поточної вибірки і не дуже чутливі до малих зсувів середніх значень вектора спостережень. Для забезпечення більшої чутливості та для підвищення ефективності визначення змін параметрів процесу, на основі застосування додаткової інформації з виконаних раніше досліджень процесу, врахування попередніх спостережень – використовують MEWMA, MCUSUM карти.

    1. Діаграма Парето


Відомий працями з розподілу багатства серед населення країн, італійський економіст Вільфредо Парето (1848 – 1923) виявив, що в Англії в ХІХ столітті 20 % населення володіли 80 % багатств. Подібну ситуацію в приблизних пропорціях можна спостерігати в усіх розвинутих країнах сучасного світу. Таким чином, принцип Парето полягає в тому, що аналізуючи показники, які характеризують групу предметів чи людей, можна констатувати, що їх мала кількість представляє собою велику значимість, тоді, як велика кількість, яка залишається, має малу значимість.

Наприклад, дуже часто мала кількість відсотків клієнтів підприємства приносить левову частку доходів.

Принцип Парето використовують під час організації постачання запасних матеріалів за методом АВС, за яким виділяються мало чисельні по номенклатурі, але важливі по витрачанню та вартості запасні частини, на які припадає більша частина грошових ресурсів, укладених у запаси (група А). Цій групі приділяють більше уваги. Група В включає запасні частини середнього попиту та не дуже значної сукупної вартості, а група С – запасні частини багато чисельної номенклатури, але малого попиту.

В сфері управління якістю принцип Парето проявляється в тому, що при великій кількості обладнання та виконавців причиною браку , звичайно, є лише деякі з них, які й можуть бути виявлені за допомогою побудови діаграми Парето.

Діаграма Парето є графічним зображенням даних, де на осях координат відкладаються види проблем, або класи об’єктів (тип дефектів), ранжовані в порядку значимості, що зменшується, та величини значимості проблем (кількість дефектів, відповідний до проблеми процент браку, вартість браку тощо). Різні класи проблем чи об’єктів зображуються прямокутниками, висота яких пропорційна ступеню їх значимості. Часто на діаграмі наносять ламану лінію, яка показує сукупну значимість різних класів проблеми, починаючи з найбільш значимого.

Приклад діаграми Парето показаний на рис.8. Діаграма побудована за даними табл.3.

Звичайно використовують два типи діаграм: частот виникнення проблем та вартостей наслідків проблем. У діаграмах першого типу по вертикальній осі відкладають частоту виникнення проблеми (кількість випадків, процент від загальної кількості випадків). У діаграмах другого типу по вертикальній осі відкладають вартість браку у абсолютній величині або в процентах від загальної вартості браку (рис.8).


Таблиця 3





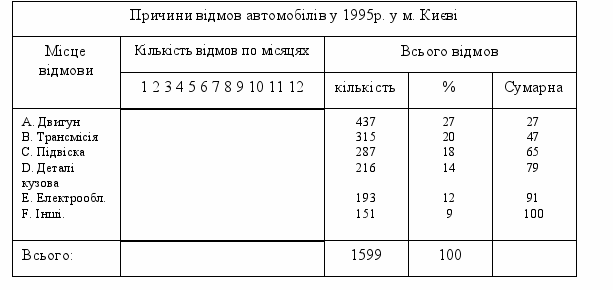
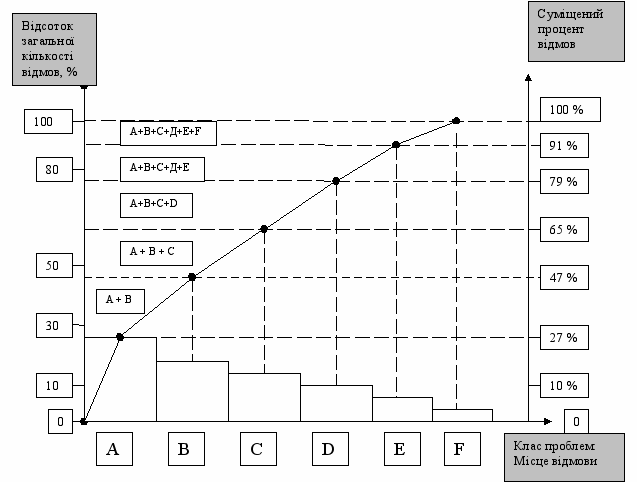
Рис.8. Діаграма Парето причин відмов автомобілів




    1. Діаграма «причини-наслідки» (Ішикави)


Варіація характеристик продукту може мати багато причин. Коли констатується статистичний сигнал, який свідчить про наявність якогось спеціального чинника, що є причиною браку, необхідно відшукати і усунути цю причину.

Діаграма «причини-наслідки» – це графічна ілюстрація процесу виявлення причин неякості [11].

Загальний вигляд діаграми Ішикави представлений на рис.9.





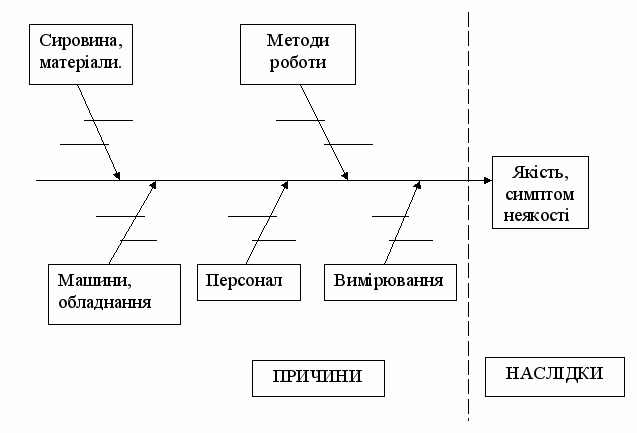
Рис.9. Діаграма Ішикави (діаграма «причин та наслідків»)


Процес виявлення причин неякості виконується групою в такій послідовності:

1. Визначають та описують з максимальною точністю продукт, процес або подію, які необхідно вивчити, характеристики , які необхідно отримати;

2. Складають список усіх можливих причин варіації результату;

3. Виділяють головні загальні причини, які прямо впливають на якість. Групують всі непрямі причини по групах та підгрупах, що входять у групи;

4. Креслять діаграму «причини-наслідки» на великому аркуші. Діаграма доповнюється в міру вивчення проблеми.

Така діаграма є візуальною підтримкою для роботи в групі. Члени групи збирають інформацію та дані, необхідні для вирішення проблеми. Якщо цього виявляється недостатньо для знайдення рішення, то група збирається ще раз через деякий час, маючи нову інформацію та нові дані. Так робиться доти, поки не буде знайдена основна причина варіації характеристики, що досліджується.

Потрібно відмітити, що не діаграма приносить рішення. Вона тільки допомагає добре поставити проблему, що дуже важливо на початку роботи. Після чого кожен член групи або відділу, які займаються якістю пропонує гіпотези, які перевіряються за допомогою статистичних методів дослідження. Після цього виробляються рішення щодо усунення причин неякості.

На рис.10 показана діаграма Ішикави із факторами, що викликають брак двигуна після ремонту. До центральної стрілки, яка показує об’єкт аналізу, підводять великі первинні стрілки, які позначають групи факторів, що впливають на об’єкт аналізу. Далі до кожної стрілки підводять стрілки другого, третього і т. п. порядку до тих пір, поки на діаграму не будуть нанесені всі стрілки, що позначають фактори, які здійснюють помітний вплив на об’єкт аналізу в конкретній ситуації.

    1. Діаграми кореляції


Діаграма кореляції є графіком, який характеризує взаємозв’язок між двома величинами А і Б (рис.11).

Для побудови діаграми кореляції спочатку збирають дані щодо пар величин А і Б. Необхідно мати не менш як 30 пар даних. Після цього на проградуйованих осях відкладають значення величин А і Б для кожної пари та позначають точкою перетин цих координат. Звичайно, параметр, що відповідає причині, відкладають на горизонтальній осі, а наслідку – на вертикальній осі.

Деякі кореляції можна легко бачити на діаграмі. У цьому випадку розташування точок має дуже витягнутий характер. У разі відсутності кореляції між двома параметрами А і Б зона розташування точок має вигляд кола.

Але в усіх випадках існує тест (метод медіан) для виявлення наявності кореляції між двома параметрами. Для дослідження необхідно провести вертикальну та горизонтальну медіани розподілу. Медіани ділять кількість точок навпіл по горизонталі та вертикалі.

Медіани розділяють діаграму кореляції на чотири зони, позначені номерами 1, 2, 3 та 4 (рис.11). Підраховують кількість точок у кожній зоні (не враховують точки, які знаходяться на медіанах). Потім вносять точки у таблицю.

Складають кількість точок у зонах 1 і 3, 2 і 4. Після цього складають два отриманих числа. Результат повинен дорівнювати кількості n точок на діаграмі, за винятком точок на медіанах.

У табл. 4 наведені граничні тестові дані залежно від кількості точок n. (при α = 0.05 – коефіцієнт ризику становить 5 %).

Якщо найменший результат серед (1 + 3) та (2 + 4) є менший за граничний з таблиці, то кореляція існує, у протилежному випадку вона відсутня.

У прикладі на рис.11 найменша сума по діагоналях квадрата дорівнює 4, кількість точок n = 22. Цій кількості точок відповідає гранична величина 5, яка є більшою за найменшу суму 4, тобто існує кореляція між величинами А і Б.





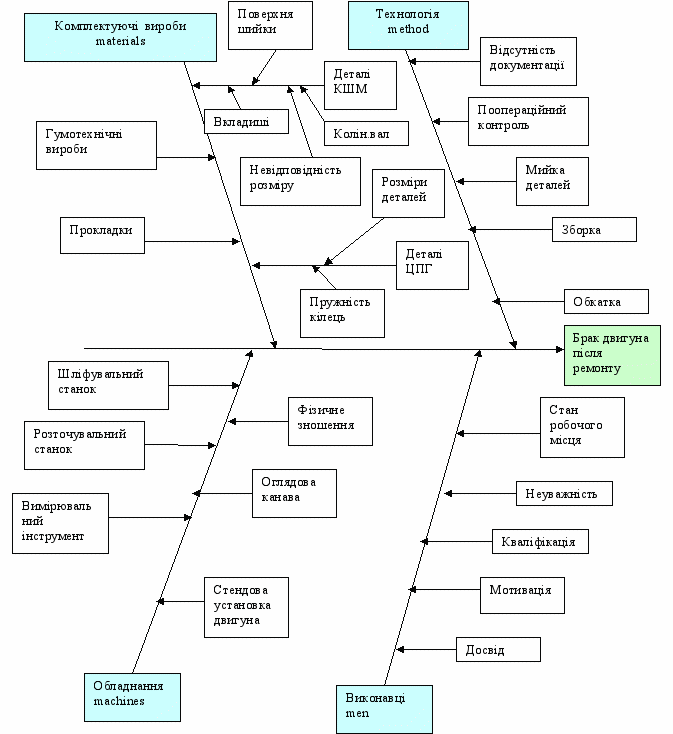
Рис.10. Діаграма Ішикави (діаграма «причин та наслідків») для визначення факторів браку двигуна після ремонту


Таблиця 4

Граничні значення тесту на кореляцію

n
lim
n
lim
n
lim
n
lim

9
1
27
7
45
15
63
23

10
1
28
8
46
15
64
23

11
1
29
8
47
16
65
24

12
2
30
9
48
16
66
24

13
2
31
9
49
17
67
25

14
2
32
9
50
17
68
25

15
3
33
10
51
18
69
25

16
3
34
10
52
18
70
26

17
4
35
11
53
18
71
26

18
4
36
11
54
19
72
27

19
4
37
12
55
19
73
27

20
5
38
12
56
20
74
28

21
5
39
12
57
20
75
28

22
5
40
13
58
21
76
28

23
6
41
13
59
21
77
29

24
6
42
14
60
21
78
29

25
7
43
14
61
22
79
30

26
7
44
15
62
22
80
30





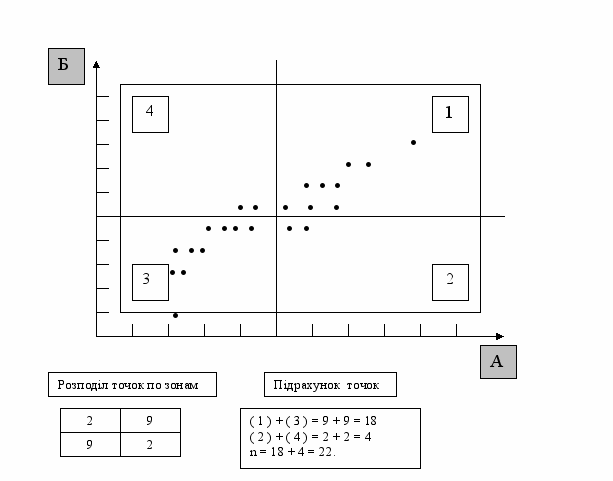
Рис.11. Діаграма кореляції


Існують різні методи оцінки наявності та ступеня кореляційної залежності (міри щільності зв’язку) двох ознак якості. Одним із них являється метод визначення коефіцієнта кореляції Пірсона r:


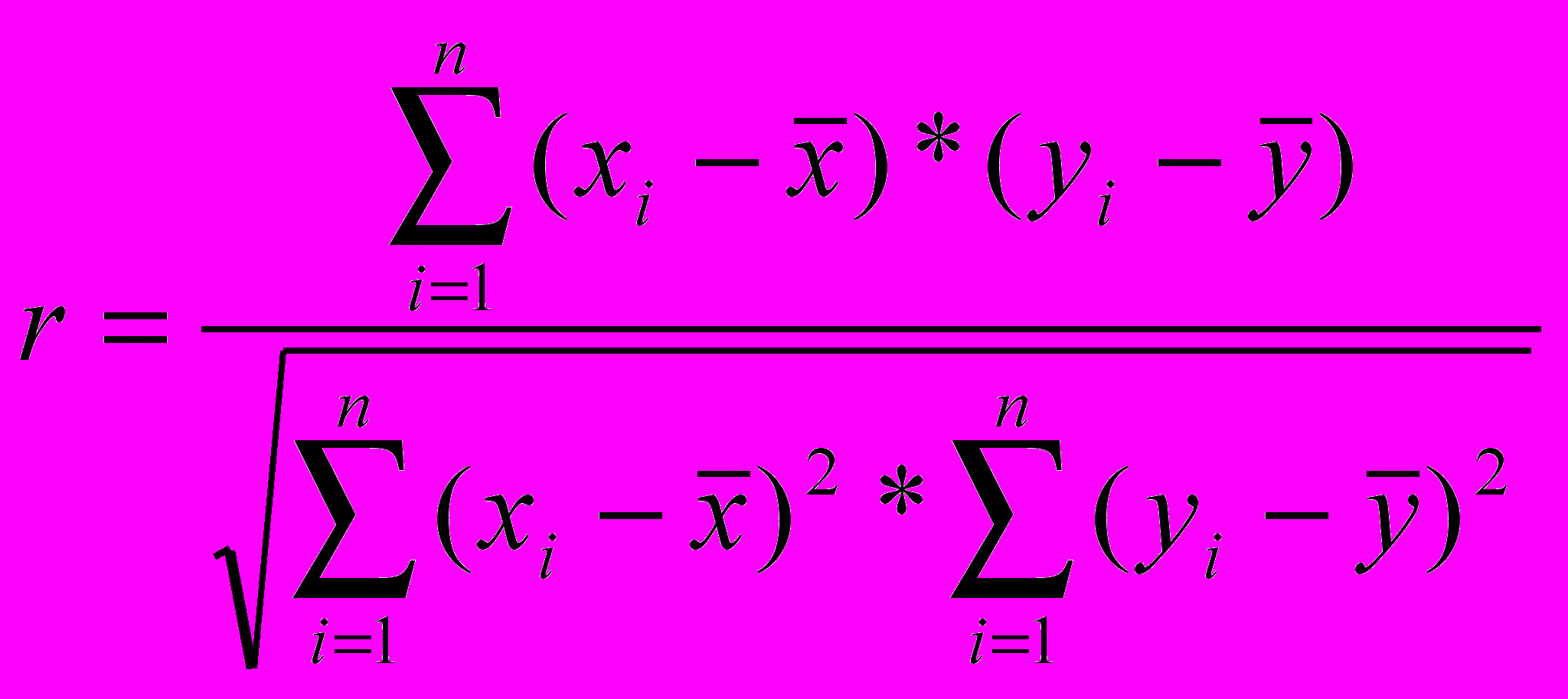, (11)


або 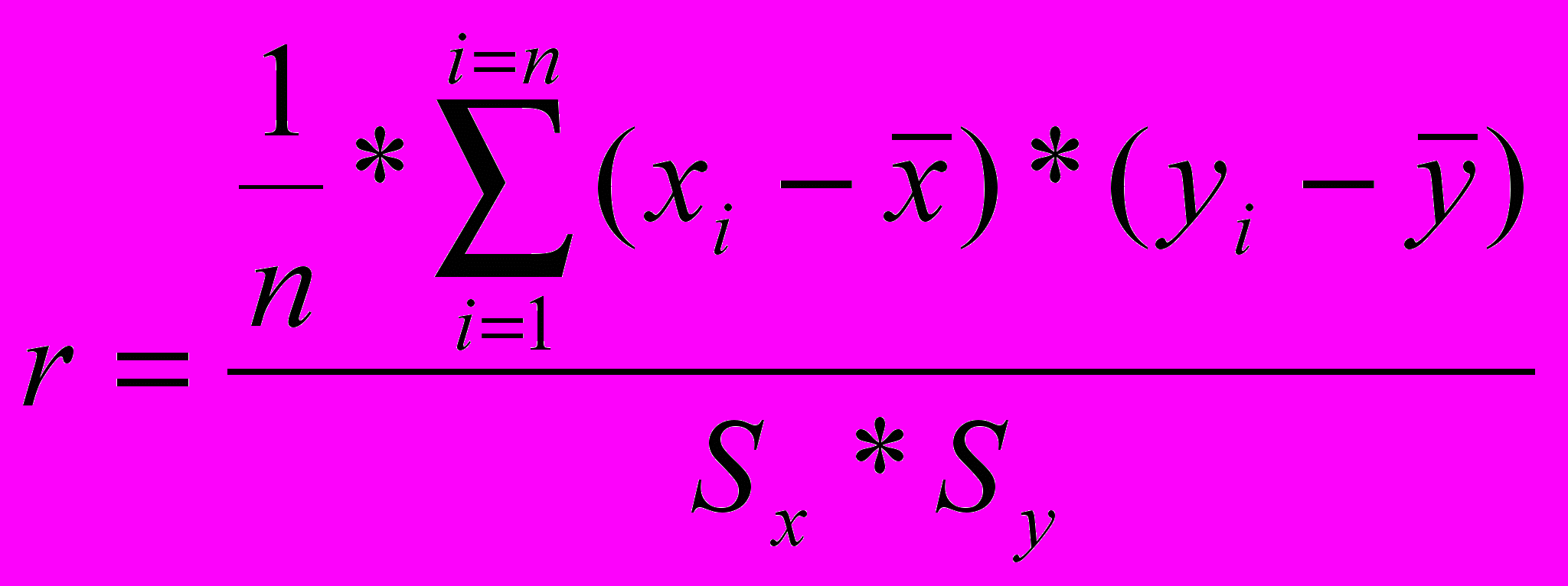. (12)

Коефіцієнт кореляції змінюється в межах [-1 ; +1], 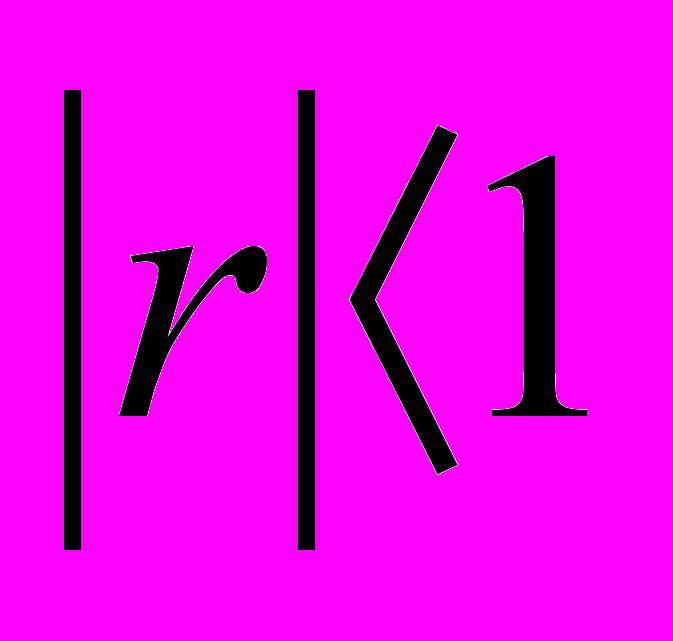. Чим більше його абсолютне значення, тим сильнішим є зв'язок між фактором та ознакою. Зокрема, при 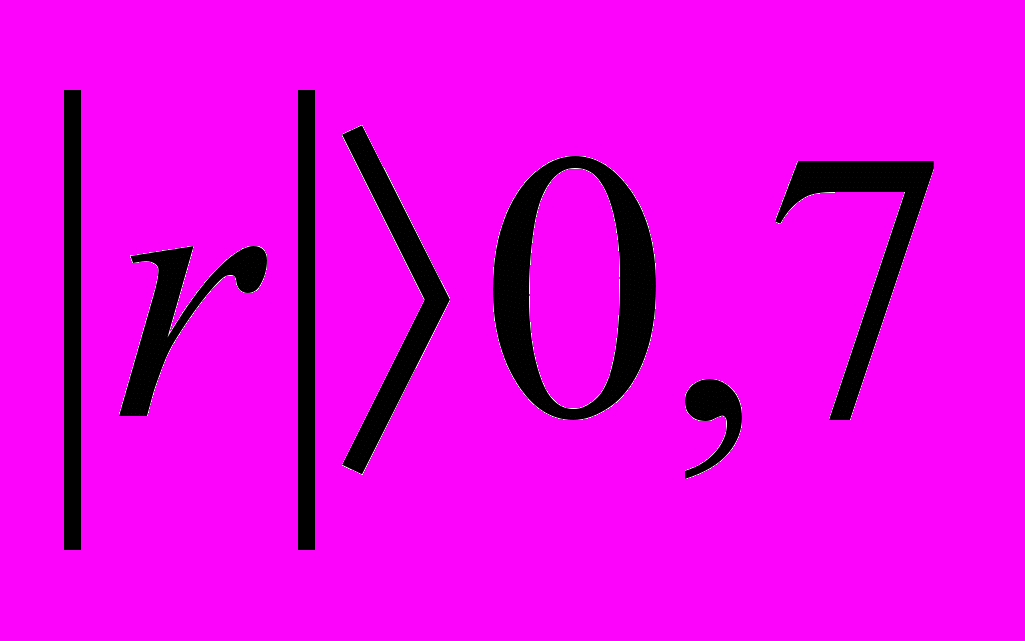зв'язок вважається значним; при 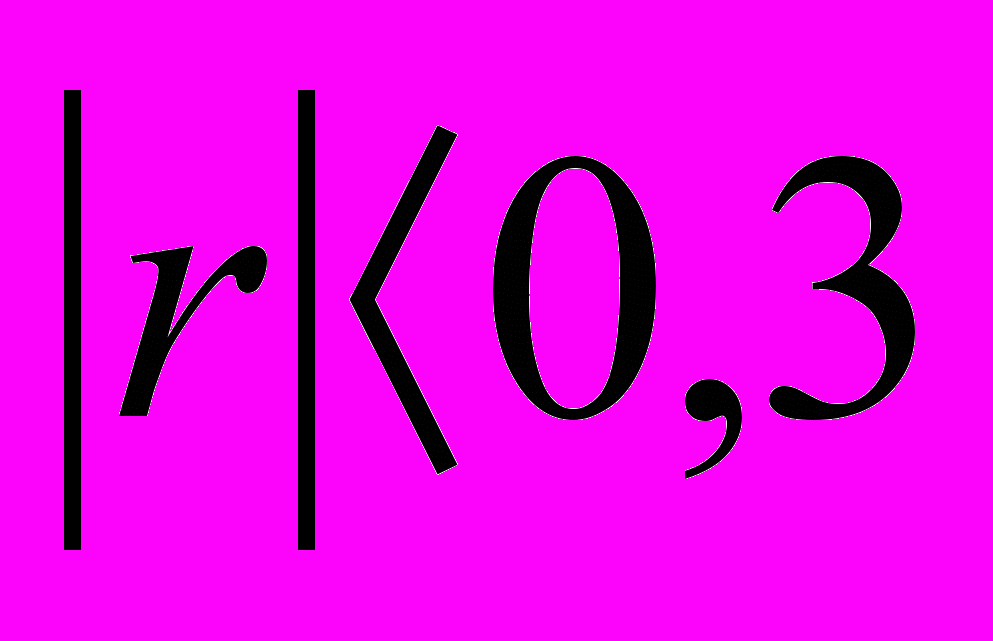– зв'язок випадковий, несуттєвий; при 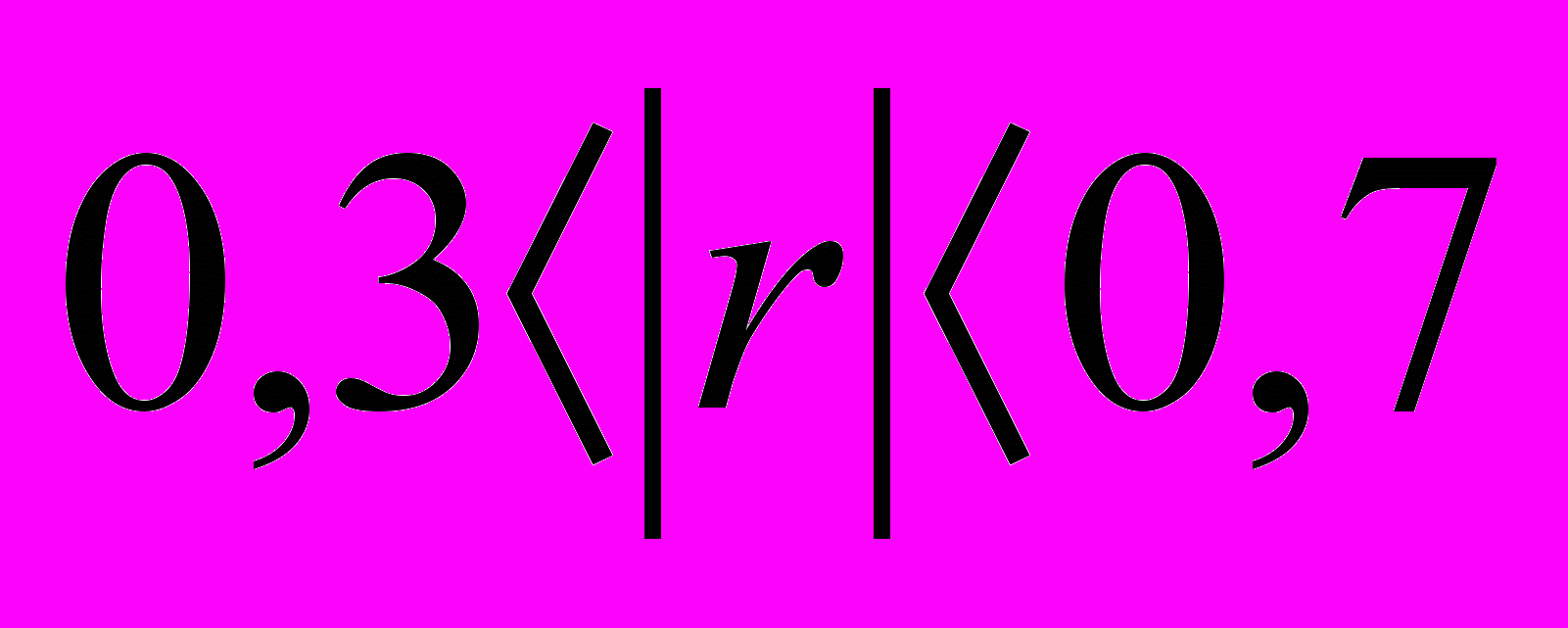– потрібно спеціально оцінити надійність зв’язку.

При значеннях більших 0 – зв'язок прямий, при значеннях менше 0 – зв'язок зворотній. При r < 0 із зростанням хі значення уі падають; при r > 0 із зростанням хі значення уі збільшуються.

    1. Групування даних


З математичної точки зору, при аналізі даних деяка кількість інформації повинна бути віднесена до кожного даного чи їх групи. Наприклад, до кількості клієнтів, яким надані послуги, відносять дату, день тижня, прізвище надавача послуг тощо.

Така дія називається групуванням даних. Таким чином, групування даних – це вибір з усієї сукупності однорідних даних за певною ознакою або згідно з визначеним принципом.

За допомогою групування намагаються створити умови, при яких отримані дані є більш однорідними і усувається вплив певних факторів.

Групування дозволяє визначити наявність кореляції там, де інакше вона не спостерігається. Приклади групованих та негрупованих даних показані на рис.12.

Як приклад, для виявлення основних факторів, які впливають на якість наданих послуг в автосервісному виробництві, було проведене анкетне опитування головних спеціалістів підприємства ВАТ ,,Автоцентр №1” [12]. В якості першого етапу із числа факторів були виділені чотири групи, які відрізняються за характером їх участі в процесі обслуговування:
  1. Техніко – економічні;
  2. Організаційні;
  3. Економічні;
  4. Соціально-економічні.




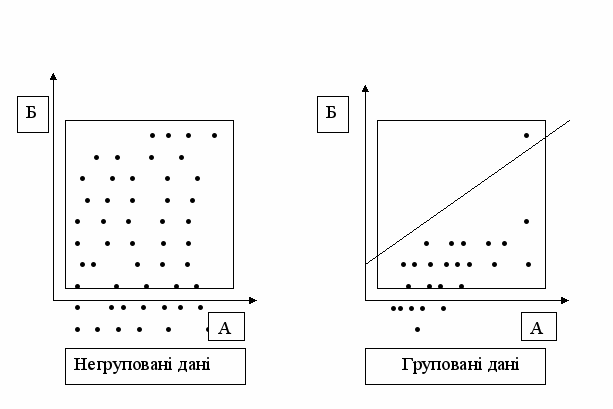
Рис.12. Груповані та негруповані дані


Залежність показника якості від факторів, які на нього впливають можна представити у вигляді:

y = f (x1, x2, x3,…, x18), (13)


де у – показник рівня якості продукції (рівня якості обслуговування автомобілів), визначається як відношення частки продукції вищої категорії якості до загального об’єму випуску, %; х1, х2,…, х18 – фактори якості (табл.5).

Оскільки вибір факторів, які впливають на показник якості, являється в певній мірі довільним, тому завжди необхідно оцінити ступінь тісноти зв’язку між ними. Силу зв’язку між факторами та показником якості (в даному випадку: між технічними, соціальними, організаційними, економічними факторами та рівнем якості наданих послуг) можна визначити за допомогою коефіцієнта кореляції, який зручно обчислювати за формулою:


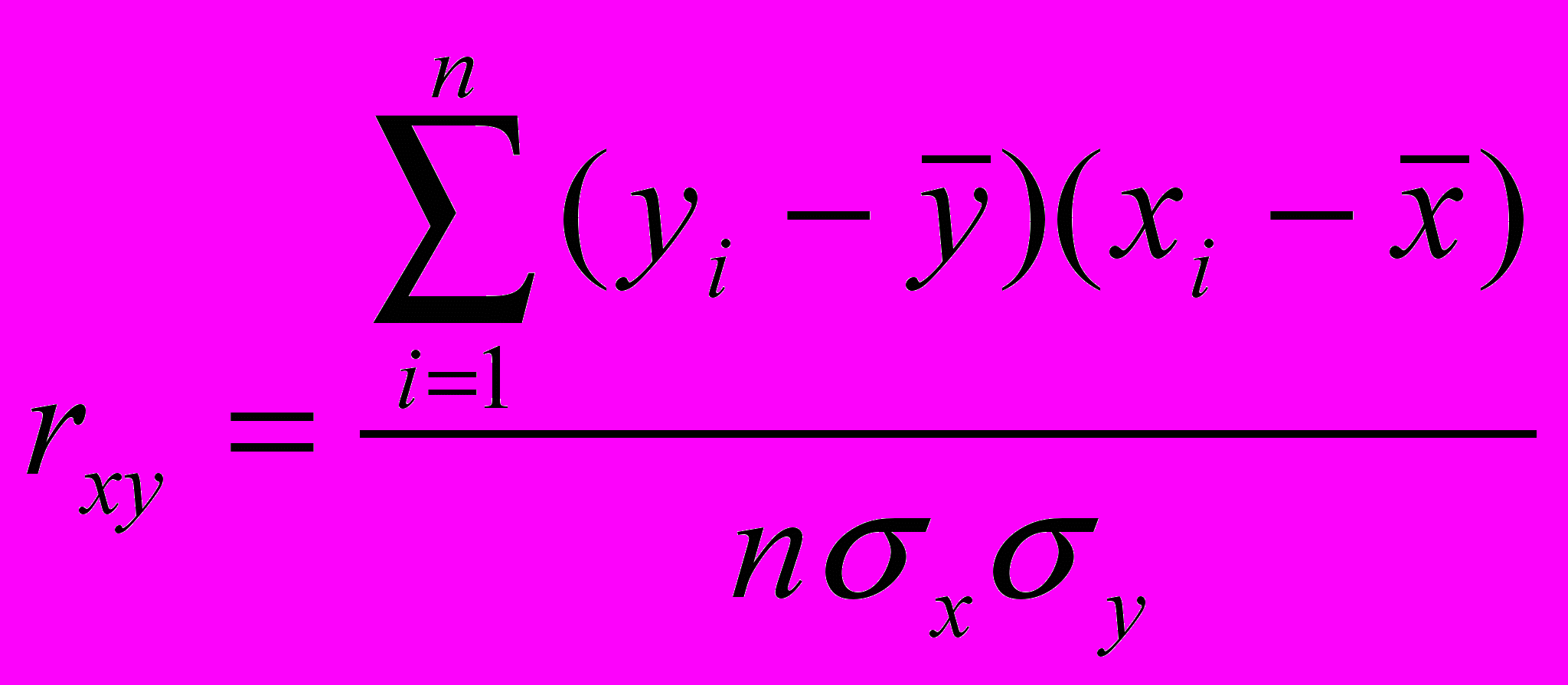, (14)


де 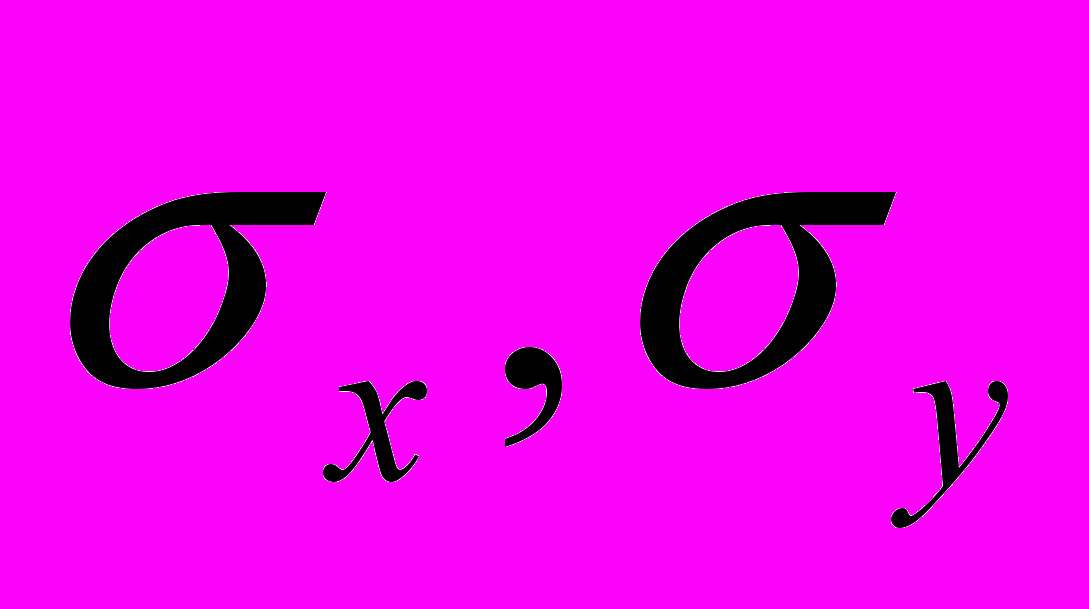– відповідно середньоквадратичні відхилення величини x, y;

і = 1, 2,…, n – кількість спостережень (значень) фактора х та ознаки у;

хі, уі – значення величини х, у для і–го вимірювання.

Значення величин х1, х2,…, х18, у наведені в табл.6 – 7.

Таблиця 5

Структура факторів, які впливають на рівень якості продукції підприємства

Технічні
Організаційні
Економічні
Соціальні

1. Рівень автоматизації та механізації виробництва (х1), %.
1. Коефіцієнт видачі автомобіля з першого разу (х9), %.
1. Сума надбавки до зарплати за вищу категорію якості (х12), грн.
1. Рівень підвищення кваліфікації працівників(х13), %.

2. Питома вага прогресивних видів машин та обладнання ( х2 ), %.
2. Рівень спеціалізації виробництва (х10), %.



2. Показник плинності кадрів (х14), %.

3. Питома вага використання прогресивних технологічних процесів

( х3), %.
3.Кількість отриманих рекламацій(х11), шт.



3. Середній стаж роботи по даній спеціальності (х15), роки.

4. Коефіцієнт оновлення основних фондів (х4), %.






4. Середній рівень освіти працівників(х16), роки.

5. Рівень якості вихідних матеріалів, запчастин, комплектуючих

( х5), %.






5. Середній вік працівників(х17), роки.

6. Ступінь зношеності обладнання (х6), %.






6. Середній розмір місячної заробітної плати виробничого персоналу (х18), грн.

7. Питома вага активної частини фондів (х7), %.









8. Фондоозброєність одного працівника по активній частині основних фондів(х8), грн.