< Предыдущая		Оглавление		Следующая >

4.5. Онтологическая концепция Идена - Тернера

Англичанин Р. Тернер в статье с характерным названием "Понимание языков программирования" обращается к их семантике. При этом он руководствуется математической парадигмой, связывая ее в основном с противостоянием математического платонизма и формализма. Согласно программе формализма, как известно, инициированной Д. Гильбертом, математическая теория оперирует формальными знаками, которые не интерпретируются на какую-либо область объектов. Такая интерпретация может иметь место, но за пределами математической теории. Следовательно, формализм откровенно ориентируется на синтактику. Принципиально иначе обстоят дела в теоретико-множественном направлении. На этот раз объекты определяются в качестве множеств. Существуют разные математические языки, но все они в конечном счете замыкаются на теорию множеств. Отсюда следует, что подлинными объектами математики являются множества. Однако они не обладают пространственно-временными признаками, следовательно, правомерно вслед за К. Гёделем признавать их абстрактными объектами, не образованными в сознании человека, а от века существующими сами по себе. В результате возрождается платонизм.

Определившись относительно математической семантики, Тернер переходит к ее компьютерному аналогу. В качестве основания для иерархии языков программирования выбирается лямбда-исчисление, а оно, в свою очередь, является спецификацией теории множеств. Но в таком случае выясняется, что объектами языков программирования вновь оказываются множества, абстрактные структуры. Тернера беспокоит различие математики и информатики. Как он полагает, математики являются платониками в течение всей рабочей недели, но на выходные дни становятся формалистами. В принципиально другой манере действуют специалисты по информатике. В течение недели они манипулируют логическими и вычислительными системами, пишут программы, проверяют их, - все эти действия имеют синтаксическую направленность. Но в выходные дни они определяют содержание и значение проделанной работы со ссылкой на универсум теории множеств.

Анализ Тернера оказался неудачным. Во-первых, недопустимо считать эквивалентными математические и компьютерные теории. Во-вторых, автор замыкает специфические теории на самые общие концепции, и именно с ними связывает подлинную природу объектов. Между тем в онтологическом отношении максимальный интерес представляют не наиболее общие, а специфические теории. Существуют не множества как таковые, а множества натуральных чисел, нелинейных или линейных функций, треугольников и окружностей. Наконец, в-третьих, Тернер пытался опереться на работы, выполненные в семантическом ключе в философии математики, однако в поле его внимания попали лишь некоторые направления анализа.

Пожалуй, наиболее впечатляющей попыткой представить компьютерную онтологию и семантику в систематическом виде стала совместная работа А. Идена и Р. Тернера "Проблемы онтологии компьютерных программ". Обширная статья начинается с трех центральных для нее вопросов:

(1) Могут ли программы, метапрограммы и аппаратное обеспечение быть упорядочены в форме тщательно осмысленной таксономии?

(2) Для какой онтологии предназначены компьютерные программы?

(3) Чем объясняется быстрое размножение языков программирования и каково их происхождение?

Авторы полагают, что ответы на эти вопросы позволяют заложить краеугольный камень в основание компьютерной онтологии. Но как же ввести различие между:

а) метапрограммами, содержащими алгоритмы, абстрактные машины и средства, необходимые для проектирования программного обеспечения,

б) программами, включая их разновидности в форме программ-текстов, программ-процессов и кодов, и

в) аппаратным обеспечением?

Размышляя над этим вопросом, авторы обращаются к теории абстракций, которым они стремятся дать исчерпывающие характеристики. В поле их зрения попадает шесть интерпретаций, комбинациями которых, как полагают авторы, исчерпываются все возможные абстракции (табл. 4.2).

Таблица 4.2. Природа абстракций в концепции Идена - Тернера

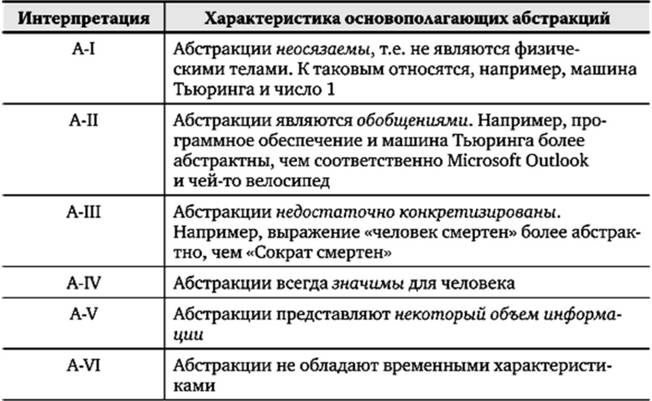
Далее Идеи и Тернер взаимно сопоставляют метапрограммы, программы и аппаратное обеспечение, с одной стороны, и абстракции - с другой. Выясняется, что абстракции можно использовать в качестве характерных признаков, выражающих специфику концептов информатики. Например, различие метапрограмм и просто программ объясняется посредством А-И: метапрограммы являются обобщениями программ. Отличие программ от аппаратного обеспечения объясняется посредством А-1: программы в отличие от аппаратного обеспечения неосязаемы и т.д. Таким образом, на сформулированный выше вопрос (1) следует отчетливый ответ: метапрограммы, программы и аппаратное обеспечение являются различными уровнями абстракций.

В попытке ответить на вопрос (2) о природе той онтологии, которой соответствуют программы, авторы прибегают к помощи парадигм программирования. Речь, в частности, идет об объектно-ориентированном, функциональном и процедурном программировании. Но хорошо известно, что парадигма программирования не определяет однозначно язык программирования: многие языки программирования являются мультипарадигмальными. Например, на языке Си, который не является объектно-ориентированным, можно писать программы, ориентированные на объекты. Авторы находят выход из этой затруднительной ситуации. По их мнению, онтология становится прозрачной лишь при соблюдении двух условий. Во-первых, язык программирования должен быть ориентирован на парадигму программирования. Во-вторых, программа, представленная текстом, является конкретизацией метапрограммы, также ориентированной на ту же самую парадигму программирования. В таком случае программа выражает онтологию, заданную парадигмой программирования.

Находится ответ и на вопрос (3) о быстром размножении языков программирования: они являются конкретизациями того или иного специфического множества метапрограмм. Каждая такая уместная, т.е. не содержащая противоречий, конкретизация приводит к новому языку.

Теория Идена -Тернера относительно природы информатики

1. Существует то, что содержится в информатике как теории.

2. Главными объектами информатики являются парадигмы вычислений и программирования, языки программирования, программы и аппаратное обеспечение.

3. Все семантические объекты информатики являются абстракциями, но неодинакового уровня.

4. Семантические объекты связаны друг с другом отношениями синтеза и конкретизации.

Следует отдать должное А. Идену и Р. Тернеру: им удалось создать многозвенную теорию семантического содержания информатики. В ней в единое целое посредством некоторых переходов объединены концепты парадигм программирования, метапрограмм, языков программирования, программ и аппаратного обеспечения. Из этих пяти концептов наиболее непривычным образованием является концепт метапрограммы. По сути, под метапрограммой понимаются парадигмы вычисления или, точнее, оперирования символами, например лямбда-исчисление. С учетом такого уточнения в семантике информатики реализуются переходы, представленные рис. 4.1. На нем переходы символизируются стрелками, которые понимаются в качестве последовательных стадий синтеза, обеспечивающих конкретизацию, где заключительным звеном оказывается аппаратное обеспечение.

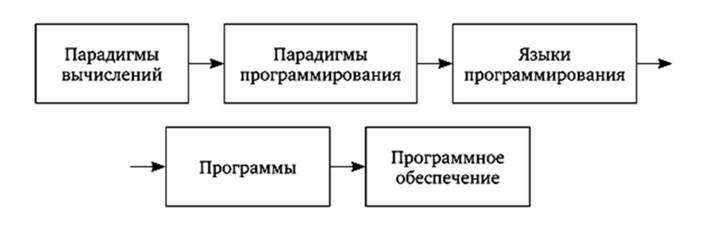
Рис. 4.1. Концептуальные переходы в семантической теории Идена - Тернера

А. Идеи и Р. Тернер полагают, что исходным уровнем компьютерной семантики являются парадигмы программирования. Однако такой вывод не соответствует главной линии их аргументации, ведь, строго говоря, парадигмам программирования предшествуют парадигмы вычислений. Это обстоятельство учтено на рис. 4.1. Мы отказались от термина "метапрограмма", поскольку использование приставки мета правомерно лишь тогда, когда речь идет о философской теории. Вся теория Идена - Тернера в целом является метаконцепцией. Что же касается парадигм компьютерных вычислений, то они играют роль принципов, ибо им в информатике ничто не предшествует. Неправомерно считать их метатеорией программ.

Авторская позиция.

Споры вокруг онтологии в информатике напоминают дискуссии, которые в течение целого века ведутся в математике. При обсуждении онтологических вопросов информатики следует иметь их в виду. Это тем более актуально, что во многих отношениях информатика и математика являются родственными дисциплинами. В табл. 4.3 приводятся наиболее актуальные онтологические концепции математики.

Таблица 4.3. Онтологические концепции математики

Философско-математическое направление	Основные представители	Природа математических объектов
Логицизм	Г. Фреге, Б. Рассел	Математические объекты имеют логическую природу
Интуиционизм	Л. Брауэр, А. Гейтинг	Математические объекты являются ментальными объектами
Конструктивизм	А. А. Марков, Э. Бишоп	Математические объекты являются составляющими языков конструирования, реализующими некоторое правило
Формализм	Д. Гильберт, Г. Генцен	Математические объекты ментальны, по своей природе они формальны, не являются абстракциями
Теоретико-множественное направление	Г. Кантор, Э. Цермело	Математические объекты являются множествами
Теоретико-категориальное направление	А. Гротендик, Ф. Лаввер	Природа математических объектов определяется теми операциями отображения, стороной которых они выступают
Платонизм	Г. Фреге, К- Гёдель	Математические объекты существуют от века, они не являются ни ментальными, ни языковыми, ни физическими по своей природе
Реализм	X. Патнэм, П. Мэдди	Математические объекты являются множествами
Натурализм	У. Куайн, П. Мэдди	Математические объекты - это то, что содержится в теории, то чем оперируют математики
Квазиэмпиризм	И. Лакатос, У. Куайн	Эксперимент затрагивает не только физические, но и математические объекты, ибо они содержатся в лучших теориях, например, физических
Фикционализм	X, Филд, М. Балагур	Математические объекты являются фикциями; это абстракции, которые не имеют реальных аналогов
Структурализм	П. Бенецараф, С Шапиро	Природу математических объектов определяют те структуры, элементами которых они выступают
Социальный конструктивизм	Р. Хёрст, П. Эрнест	Математические объекты являются разновидностями социально-исторических объектов, ибо они реализуются в соответствующих практиках

Обобщая концепции, представленные в табл. 4.3, можно выделить семь подходов:

I. Математические объекты считаются неразрывно слитыми с природными реалиями. Такой подход характерен для квазиэмпириков, а также отчасти для реалистов.

II. Математические объекты признаются абстракциями от природных объектов. Такой позиции придерживаются большинство представителей теоретико-множественного направления.

III. Математические объекты считаются абстракциями не потому, что они представляют собой обедненные конкретные объекты, а исключительно в силу их несхожести с привычными для нас физическими объектами. Такой позиции придерживаются, например, платоники.

IV. Математические объекты считаются абстракциями-фикциями, имеющими вспомогательное значение. Такова позиция фикционалистов.

V. Математические объекты определяются на основании самых общих теорий, например в качестве множеств, категориальных объектов, структур.

VI. Математические объекты признаются теоретическими (в рамках натурализма).

VII. Математические объекты приравниваются к объектам логики (в рамках логицизма) или же социальных наук (социальный конструктивизм).

Подход VII является несостоятельным, поскольку в нем недооценивается специфика непосредственно математических объектов. Здесь разумно вспомнить, что, как уже отмечалось, несостоятельно сводить объекты информатики к математическим объектам. Подходу VI, несмотря на его актуальность в смысле борьбы против недооценки теорий, недостает специфики: мало подчеркивать, что объекты информатики теоретичны, - их еще необходимо как-то называть. В рамках подхода V математические объекты отождествляются с объектами самых общих теорий. При этом не учитывается, что общие определения непременно следует доводить до самого нижнего уровня их спецификации, поскольку в противном случае велик риск остаться на уровне номинальных, а не концептуально-реальных определений. Показательный пример: объектами арифметики являются не множества, а множества натуральных чисел. При подходе I вновь недостаточное внимание уделяется специфике математических объектов, к тому же отодвигается в тень теоретическое понимание сути дела.

В границах подходов II-IV математические объекты признаются абстракциями, но в силу различных оснований, при этом возникают новые коллизии. Так, платоники считают математические объекты самостоятельными сущностями, несводимыми либо к ментальным, либо к языковым образованиям. Фикционалисты отказываются признавать математические объекты столь же самостоятельными, как, например, физические. Для них математические объекты являются фикциями ума. Интуиционисты и конструктивисты занимают промежуточное положение между фикционалистами и платониками. Они считают математические объекты более основательными, чем фикции, но не придают им самостоятельного значения, как это делают платоники. Видимо, согласно интуиционистам и конструктивистам, математические объекты являются не чем иным, как ментальными или же языковыми образованиями. Но в таком случае непонятно, почему математика, как выражался физик Э. Вигнер, столь непостижимо эффективна в горизонтах буквально всех наук.

Нетрудно видеть, что в онтологии информатики повторяются метаморфозы онтологии математики. Объекты информатики определяются в качестве абстракций, а также посредством ссылок на самые общие теории, например парадигмы информатики и парадигмы программирования. Нижний уровень абстракции в математики то и дело приписывается физике как теории физических объектов, а в информатике - аппаратному обеспечению.

Выводы

1. Объектами информатики являются все ее концепты - как элементарные, например символы, так и сложные, в частности программы. Они образуют иерархию не абстракций, а изоморфизмов.

2. Из всех объектов информатики наиболее простыми являются составляющие аппаратного обеспечения, в частности ячейки памяти. Аппаратное обеспечение - основа информатики, придающая онтологическим реалиям искомую основательность.

3. Концептуальные переходы в онтологии должны непременно доводиться до аппаратного обеспечения. Это служит гарантией от превращения объектов информатики в чисто ментальные и языковые образования, лишенные всякой телесности.

4. Объекты информатики не обладают физической телесностью, но тесно связаны с нею.

5. Природа объектов информатики разъясняется в концептуальных переходах, характерных для информатики.

< Предыдущая		Оглавление		Следующая >