Авторефераты по всем темам >>
Авторефераты по техническим наукам
Совершенствование технологического процесса и технических средств калибрования клубней картофеля
Автореферат докторской диссертации по техническим наукам
| Страницы: | 1 | 2 | 3 | |
Во второй главе Некоторые физико-механические свойства клубней картофеля изложены результаты исследования некоторых физико-механических свойств клубней картофеля, номенклатура которых, в основном, предопределена выдвинутой рабочей гипотезой и в многочисленных, имеющихся на эту тему исследованиях, практически не встречается.
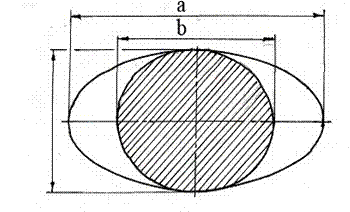Новые сорта картофеля, многие из которых зарубежной селекции, получающие в последние годы все большее распространение в Приволжском федеральном округе, имеют клубни двух геометрических форм.
Около 20% сортов имеют округлую форму и около 80% - удлиненно-овальную и длинно-овальные формы.
Для характеристики формы таких клубней было введено, ранее не используемое для клубней картофеля, понятие индекса формы и определены зависимости этого показателя от массы клубней.
На рисунке 1 показаны геометрические параметры таких клубней, по которым определены индекс формы по ширине:
а, (1)
и индекс формы по длине:
а,аа а(2)
где 
а
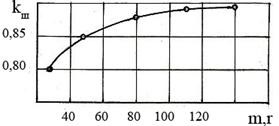
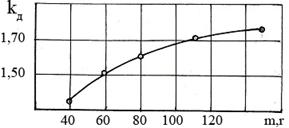
На рисунках 2 и 3 представлены зависимости индекса формы удлиненно-овальных клубней от их массы, из которых видно, что оба вышеприведенные индекса формы с увеличением массы клубней до 120-140 г увеличиваются по зависимостям аналогичного характера, а при дальнейшем увеличении массы становятся постоянными.
Для научно-обоснованной адаптации формы калибрующих отверстий к различным формам клубней исследования были направлены на математическое описание контуров их продольных и поперечных сечений.
Такое представление формы клубней позволило более аргументировано и теоретически обоснованно подойти к выработке методики построения формы и определения размеров отверстий решет картофелесортировальных машин.
инии поверхности сечения клубней исследованных сортов аэкспериментально определялись путем разрезания клубней по главным взаимно перпендикулярным осям и обводились по контуру на бумаге.
аЛинии контура по осям х и у (рисунки 4,5,6) делились на равные интервалы и для каждой точки определялись координаты, подвергавшиеся в дальнейшем статистической обработке. По полученным координатам определялись средние значения, по которым строились экспериментально полученные линии контуров.
На рисунке 4 представлены линии поверхности сечения клубня округлой формы, полученные экспериментально (кривая 1) по фактически полученным координатам (таблица 1).
Таблица 1 - Параметры линии поверхности сечения клубня округлой формы
x, мм |
0 |
5 |
10 |
15 |
20 |
24,8 |
yэ, мм |
24,8 |
23,7 |
21,9 |
18,8 |
13,9 |
0 |
yт, мм |
24,8 |
24,3 |
22,7 |
19,7 |
14,7 |
0 |
?y, % |
0 |
2,5 |
3,7 |
4,9 |
5,6 |
0 |
?yср = 4,2% |
||||||
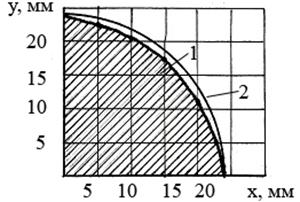Как видно из рисунка 4 часть окружности (линия 2) и контур поверхности сечения клубня (кривая 1) достаточно близки, что дает основание считать, что клубень в сечениях имеет форму окружности с параметрическим уравнением:
аа (3)аа а
Численные значения экспериментальных значений координат кривой 1 позволяют получить уравнение этой линии путем
вычисления интерполяционного многочлена, имеющего вид:
а(4)
аПо данным таблицы и вычислений можно сделать вывод, что с погрешностью в среднем равной 4,2% клубни такого вида гипотетически могут быть приняты за шар.
По аналогичной методике исследованиям были подвергнутыа клубни удлиненно-овальной формы. На рисунке 5 представлены экспериментальная линия контура поверхности клубня в поперечном сечении (линия 1), на рисунке 6 в продольном сечении (линия 1). По внешним признакам линии 1 на рисунках 5 и 6 более всего соответствуют эллипсу, параметрическое уравнение которого имеет вид:
а (5)
где 
и 
соответственно большая и малая полуоси эллипса.
Из уравнения (5) можно определить:
аа(6)
Задаваясь значениями х с равным шагом для поперечного и продольного сечений, получены теоретические значения ординат ут для эллипса с известными полуосями, по которым построены теоретические кривые (линии 2 на рисунках 5 и 6).
Полученные численные значения координат представлены для поперечного сечения клубня в таблице 2, для продольного - в таблице 3.
Таблица 2 - Параметры линии поверхности поперечного сечения
клубня удлинённо-овальной формы
x, мм |
0 |
5 |
10 |
15 |
20 |
23,4 |
yэ, мм |
19,7 |
18,6 |
17,0 |
14,4 |
9,6 |
0 |
yт, мм |
19,7 |
19,2 |
17,8 |
15,1 |
10,2 |
0 |
?y, % |
0 |
3,2 |
4,7 |
4,9 |
6,2 |
0 |
?yср = 4,75% |
||||||
Как видно из таблицы 2 в поперечном сечении контур поверхности клубня отличается от эллипса в среднем на 4,75%. Интерполяционный многочлен, описывающий линию поверхности поперечного сечения удлиненно-овального клубня, имеет вид:
а (7)
Таблица 3 - Параметры линии поверхности продольного сечения
клубня удлинённо-овальной формы
x, мм |
0 |
7 |
14 |
21 |
28 |
32,6 |
yэ, мм |
20,1 |
19,1 |
17,6 |
14,1 |
9,6 |
0 |
yт, мм |
20,1 |
19,6 |
18,2 |
15,4 |
10,3 |
0 |
?y, % |
0 |
2,6 |
3,4 |
9,2 |
7,3 |
0 |
?yср = 5,6% |
||||||
По данным таблицы 3 получен интерполяционный многочлен экспериментальной (фактической) линии поверхности продольного сечения клубня, имеющий вид:
а (8)
Как показывают данные таблицы 3, в продольном сечении контур поверхности клубней отличается от эллипса в среднем на 5,6%.
Вышеизложенное дает основание с достаточной степенью достоверности сделать вывод, что удлиненно-овальные клубни картофеля гипотетически можно считать трехосными эллипсоидами.
В третьей главе Теоретическая модель процесса формирования рациональной решетной поверхности и взаимодействия с ней клубней различной формы изложена концепция формирования новых решетных поверхностей, сочетающих в себе максимально возможные точность калибрования клубней и коэффициент пропускной способности, и построена теоретическая модель процесса взаимодействия клубней картофеля с новой калибрующей поверхностью.
Таким образом, около 20% сортов картофеля имеют форму клубней близкую к шаровидной, которые достаточно четко делятся на размерные фракции калибрующими поверхностями с квадратными отверстиями.
Около 80% сортов имеют форму клубней гипотетически представляющих собой трехосный эллипсоид. Особое значение форма клубней и калибрующих отверстий приобретают после введения новых стандартов на разделение клубней по размеру максимальной величины поперечного сечения, т.е. для клубней в форме трехосного эллипсоида - большой оси эллипса поперечного сечения. С этой точки зрения для таких клубней наиболее высокой точностью калибрования обладают решета с круглыми отверстиями.
Другим важным оценочным фактором решетных поверхностей является их производительность, в значительной степени зависящая от коэффициента пропускной способности ?пр.
Теоретически даже при касании круглых отверстий, что практически неосуществимо, т.к. между ними должны быть перемычки между отверстиями, коэффициент пропускной способности может быть:
а а(9)
В действительности при наличии перемычек этот коэффициент у решет с круглыми отверстиями составляет 0,60 - 0,70.
Наиболее близко к форме окружности подходит форма многоугольника, вторым свойством которого должна быть возможность формирования рабочего поля решета с минимальной площадью перемычек. Такой фигурой является правильный шестиугольник. Оценивая правильный шестиугольник как возможную форму отверстий решет картофелесортировальных машин, можно сделать вывод, что он близок к окружности, его диагональ от диаметра вписанной окружности по длине отличается только на 15%, а максимальное теоретическое значение коэффициента пропускной способности, без учета диаметра прутков его образующих, составляет:
а (10)
Сравнивая полученные значения коэффициента пропускной способности с аналогичным показателем для решет с круглыми отверстиями, можно заключить, что он превышает его на 15%.
Однако вышеизложенные гипотетические предпосылки требуют более детальных теоретических и экспериментальных подтверждений.
Определение теоретической погрешности точности калибрования клубней с эллипсовидными сечениями при прохождении в квадратные и правильные шестиугольные отверстия.
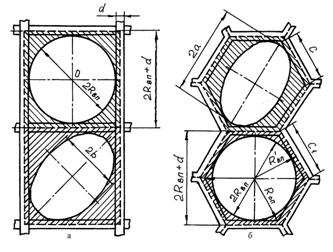
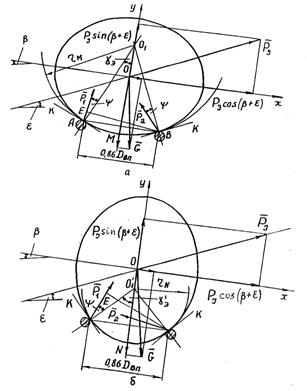
При прохождении клубней с эллипсовидными сечениями в квадратное отверстие их ориентация будет оказывать существенное влияние на точность калибрования. В зависимости от ориентации (рисунок 7а) они могут располагаться либо большой осью эллипса параллельно стороне квадрата (эллипс I), либо совпадать с диагональю квадрата (эллипс II), которая по длине сторону квадрата превосходит в 1,41 раза, что и будет приводить к погрешности в точности калибрования клубней.
Возможный минимальный размер клубня, проходящего в квадратное отверстие, будет соответствовать большой оси эллипса поперечного сечения клубня, равной стороне квадрата.
Для установления разницы размеров клубней, проходящих в одно и то же квадратное отверстие, необходимо определить и сопоставить большие оси эллипсов A1C1 при параллельности оси клубня стороне АD и при совпадении большой оси эллипса B1D1 с диагональю квадрата ВD.
Рассмотрим квадрат АВСD со стороной 2d, в который вписано два эллипса I и II с центром в точке О. Оси координат хОу расположим так, чтобы их начало расположилось в точке О, а оси были направлены по диагоналям квадрата.
Большая ось эллипса I - A1C1=2а1 параллельна и равна стороне 2d, большая ось эллипса II - B1D1=2а2 совпадает с диагональю квадратного отверстия. Малые оси эллипсов обозначим С2D2= 2b1 и С1D1= b2.
По одному из определений эллипс представляет собой фигуру, полученную путем равномерного сжатия окружности, при этом большая ось эллипса является осью сжатия.
Из этого определения следует, что в общем виде для любого эллипса справедливо соотношение:
, (11)
где k - коэффициент сжатия эллипса;
(1Цk) - сжатие эллипса;
b - малая полуось эллипса;
a - большая полуось эллипса.
В научных работах, затрагивающих изучение формы плодов сельскохозяйственных культур, в качестве параметра характеризующего форму плода, используется индекс формы. В рассматриваемом случае величина k будет не что иное, как индекс формы клубня картофеля в соответствующем сечении.
Для определения разницы в размерах клубней, способных пройти в одно и то же квадратное отверстие, необходимо математическиа связать размеры отверстия и оси эллипсов I и II.
Для этого воспользуемся уравнением касательной к эллипсу, поскольку стороны квадрата являются касательными к обоим эллипсам I и II, которое дает возможность установить связь между координатами точек эллипса и его полуосями:
.аа аа(12)
Максимальный размер поперечного сечения клубня, могущего пройти в квадратное отверстие, будет определяться абсциссой точки D1, ордината которой равна нулю:
.аа а(13)
Уравнение (13) дает возможность установить взаимосвязь между параметрами квадратного отверстия со сторонами 2d и вписанного в него эллипса II с большой осью B1D1 = 2a2. Для этого рассмотрим точку D - вершину квадрата, лежащую на оси x и также принадлежащую касательной mm, и рассмотрим только положительное направление оси x.
В этом случае уравнение (13) для точки D примет вид:
. (14)
С другой стороны, из ?OCD xD = OD будет равно 0,705d.
Тогда уравнение (14) можно записать в виде:
.аа аа(15)
Решая уравнение (15) относительно a2, получим:
.аа (16)
Большая ось эллипса II, вписанного в квадратное отверстие со стороной 2d, определится из выражения:
.аа (17)
Уравнение (17) и определяет взаимосвязь квадрата со стороной 2d и вписанного в него эллипса II с большой осью 2a2.
Результаты расчетов, выполненных по уравнению (17) для различных значений индекса формы клубней k представлены в таблице 4.
Анализ данных таблицы 4 показывает, что чем меньше индекс формы поперечного сечения клубней, тем больше разница размеров клубней, проходящих в одно и то же квадратное отверстие. Из всех сортов картофеля с эллипсовидным поперечным сечением клубней, внесенных в Госреестр, наиболее распространенными являются сорта с индексом формы поперечного сечения 0,7-0,9.
При сортировании таких клубней на размерные фракции на решетах с квадратными отверстиями диапазон варьирования их размеров при прохождении в отверстия одного и того же размера может достигать 30%. Т.е. сама конструкция квадратных отверстий теоретически заранее предполагает, что погрешность при сортировании может в два раза превышать нормы, оговоренные агротехническими требованиями.
Таблица 4 - Влияние индекса формы на размер клубней, проходящих в квадратное
отверстие постоянного размера
Индекс формы k |
Размер большой оси эллипса II (2a2) |
Размер большой оси эллипса I (2a1) |
Разница |
|
2a2 - 2a1 |
% |
|||
0,6 |
2,40d |
Постоянен и равен стороне квадратного отверстия 2d |
0,4d |
40 |
0,7 |
2,30d |
0,3d |
30 |
|
0,8 |
2,20d |
0,2d |
20 |
|
0,9 |
2,10d |
0,1d |
10 |
|
1,0 |
2,00d |
0,0d |
0 |
|
Это дает основание сделать вывод о том, что при использовании решет с квадратными отверстиями при калибровании клубней картофеля с эллипсовидными поперечными сечениями выполнение агротребований практически невозможно.
По аналогичной с предыдущей методикой определим, какова ожидаемая теоретическая величина погрешности точности сортирования может быть достигнута при использовании решет с отверстиями правильной шестиугольной формы.
В зависимости от ориентации клубня с эллипсовидным поперечным сечением при прохождении в шестиугольное отверстие (рисунок 7б) он может занять положение при совпадении большой оси эллипса A1D1 = 2a2 (эллипс II) с диагональю шестиугольника AD, равной диаметру описанной окружности, или с отрезком B1E1 = 2a1 (эллипса I), являющимся диаметром вписанной в шестиугольник окружности.
В рассматриваемом случае стороны шестиугольного отверстия также будут касательными к обоим эллипсам, из уравнения которых определится взаимосвязь между координатами точек эллипса, его большой полуосью и индексом формы k - коэффициентом сжатия эллипса:
.аа (18)
Поскольку точка D принадлежит касательной nn, а yD = 0, то для этой точки уравнение (18) запишется следующим образом:
.а (19)
Уравнение (19) дает возможность определить абсциссу точки D и связать величину a2 вписанного эллипса II с параметром правильного шестиугольника отрезком OD, являющимся радиусом Rоп описанной окружности и равным стороне правильного шестиугольника:
.а (20)
Известно, что радиус описанной окружности вокруг правильного шестиугольника с радиусом вписанной окружности связан соотношением:
. (21)
Подставив значение Rоп из (21) в (20) и выполнив преобразования, получим:
.аа аа(22)
Взяв положительное направление оси x, определим:
.а (23)
Из рисунка 7б авидно, что большая ось эллипса I будет равна двум радиусам вписанной в правильный шестиугольник окружности. Тогда уравнение (23) можно записать в виде:
.аа аа(24)
Для определения взаимосвязи больших осей эллипсов I и II правую и левую части уравнения (24) умножим на два и получим:
. (25)
Уравнение (25) дает возможность сопоставить величины больших осей эллипсов I и II в зависимости от индекса формы клубней и определить численные значения теоретической погрешности точности калибрования решетами, образованными правильными шестиугольниками, которые представлены в таблице 5.
Таблица 5 - Влияние индекса формы на размер клубней, проходящих в отверстие постоянного размера правильной шестиугольной формы
Индекс формы k |
Размер большой оси эллипса II (2a2) |
Размер большой оси эллипса I (2a1) |
Разница |
|
2a2 - 2a1 |
% |
|||
0,6 |
2,18a1 |
Постоянен и равен диаметру окружности, вписанной в шестиугольник (2a1) |
0,18a1 |
18 |
0,7 |
2,15a1 |
0,15a1 |
15 |
|
0,8 |
2,10a1 |
0,10a1 |
10 |
|
0,9 |
2,05a1 |
0,05a1 |
5 |
|
1,0 |
2,00a1 |
0,00a1 |
0 |
|
Анализ данных таблицы 5 и их сравнение с результатами таблицы 4 показывают, что теоретически возможная погрешность точности калибрования клубней с эллипсовидными сечениями на решетах с отверстиями правильной шестиугольной формы в два раза меньше, чем при использовании квадратных отверстий.
При определении производительности решетных поверхностей в машинах для сортирования зерна одним из основных факторов является коэффициент пропускной способности ?р, определяемый как отношение площади отверстий к площади рабочей поверхности решета, что равносильно отношению площади отверстия к площади решета, приходящейся на одно отверстие:
, (26)
где Fот - площадь отверстия;
FР - площадь решета, приходящаяся на одно отверстие.
Опыт работы по совершенствованию калибрующих поверхностей картофелесортировальных машин позволил ввести еще один, ранее не используемый показатель эффективности работы этих устройств - коэффициент использования площади отверстий, т.к. для картофелесортировальных машин характеристика (26) необходима, но недостаточна.
Коэффициент использования площади отверстия решета ?от, определяется как отношение площади поперечного сечения клубня при его прохождении в отверстие, к площади отверстия:
. (27)
Предложенный показатель ?от является дополнительной объективной характеристикой, оценивающей пропускную способность решет картофелесортировальных машин, т.к. учитывает не только конструктивные особенности исполнения решет, но и форму калибруемых клубней.
Площадь поперечного сечения клубней эллипсоидной формы:
.аа (28) а
Формула (28) является универсальной для любой формы поперечного сечения клубней, т.к. при k=1 превращается в площадь круга.
Подставив в формулу (27) значения Fкл и Fот, получим для квадратных отверстий:
,аа (29)
для шестиугольных:
.а (30)
Сравнение коэффициентов подсчитанных по формулам (29) и (30) для реальных значений индекса формы клубней k от 1 (округлые) до 0,9 - 0,6 (эллипсоидные) представлено в таблице 6.
Таблица 6 - Влияние индекса формы клубней и формы отверстий на коэффициент пропускной способности и использования площади отверстия
Индекс формы клубней k |
Коэффициент использования площади отверстий решет |
?от 6 > ?от 4, % |
|
квадратных ?от 4 |
шестиугольных ?от 6 |
||
1,0 |
0,785 |
0,907 |
13,45 |
0,9 |
0,706 |
0,816 |
11,00 |
0,8 |
0,628 |
0,726 |
9,80 |
0,7 |
0,548 |
0,635 |
8,60 |
0,6 |
0,471 |
0,544 |
7,30 |
Анализ данных таблицы 6 показывает, что коэффициент использования площади отверстий при любых значениях индекса формы клубней у отверстий правильной шестиугольной формы больше, чем у квадратных, а следовательно, на единице площади решета при равных радиусах вписанных окружностей, шестиугольных отверстий разместится на 14% больше, что также способствует повышению пропускной способности.
В известных работах, рассматривающих процесс взаимодействия обрабатываемого или транспортируемого материала с колеблющимися наклонными поверхностями, компоненты материала, как правило, рассматриваются либо как материальные точки, либо как тела неопределенной формы с известной массой и центром тяжести, без учета геометрической формы и размеров, а сами рабочие органы - в виде плоскости без детализации ее конструктивных особенностей, за исключением ступенчатых поверхностей.
Такой подход дает только общее представление о процессе, но не выявляет воздействия на процесс формы и размеров калибруемых предметов и конструктивных особенностей колеблющейся наклонной поверхности, оказывающих существенное влияние на кинематику и динамику процесса.
Для функционирования технологического процесса клубни, идущие по поверхности решета сходом должны перемещаться по ней.
Рассмотрим процесс взаимодействия с решетной поверхностью, образованной правильными шестиугольными отверстиями клубней округлой формы, которые для теоретического исследования могут быть приняты за шар.
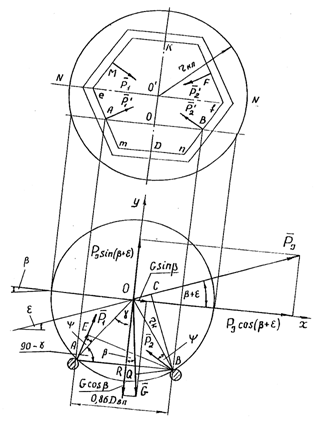Шар в отверстии опирается на его ребра в точках ADBFKM (рисунок 9), расположенных в середине сторон шестиугольника. Начальный момент выкатывания клубня наступает при его равновесии в отверстии.
Взаимосвязи геометрических параметров клубня и отверстияа определим рассмотрев сечение по линии АОВ вертикальной плоскостью перпендикулярной площади решета и параллельной диагонали отверстия ef.
Это сечение (рисунок 10) дает возможность установить связь между размерами клубня и отверстия решета.
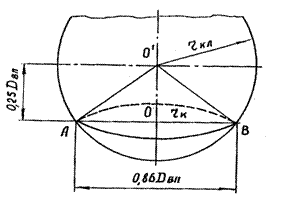
Как видно из рисунка 9 хорда АВ является средней линей трапеции mefn, и, следовательно отрезок ОО1 равен половине радиуса окружности, вписанной в шестиугольное отверстие. Обозначим радиус шаровидного клубня rкл, а мгновенный радиус качении клубня rк.
Из геометрических соотношений получим: а
, аа (31)
где Dвп - диаметр окружности, вписанной в шестиугольное отверстие.
Мгновенный радиус качения клубня: а
. (32)
Для определения условий равновесия клубня, находящегося в отверстии решета, воспользуемся прямоугольной системой координат хОу (рисунок 9), ось Ох которой направим параллельно поверхности решета с положительным направлением по ходу технологического процесса, а сумму моментов возьмем относительно точки В, вокруг которой клубень будет поворачиваться при перекатывании.
Условие равновесия примет вид системы уравнений:
,аа (33)
, (34)
.а а(35)
где PJ - сила инерции клубня, Н; ? - угол наклона решета к горизонту, град; ? - угол наклона к горизонту линии действия шатуна, град; G - сила тяжести клубня, Н; P1 - проекция на вертикальную плоскость суммарной реакции в точках опоры A и M, Н; ? - угол трения качения клубней по решётной поверхности, град; ? - угол между мгновенным радиусом качения клубня rк и осью Oy, град.
;
P2 - проекция на вертикальную плоскость суммарной реакции в точках B и F; ВС - плечо силы PJ: 
; ВЕ - плечо силы P1: 
; ВQ - плечо силы G: 
.
Решим систему уравнений (33)-(35), введя замену: PJ=m?2A и G=mg:
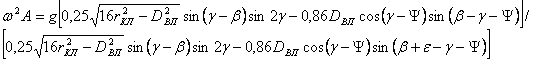аа (36)
Уравнение (36) характеризует равновесное состояние клубней в отверстиях решета и устанавливает связь между свойствами калибруемых клубней (радиус rкл, угол трения по решётной поверхности ?), параметрами картофелесортировки (диаметр вписанной в шестиугольное отверстие окружности Dвп, угол наклона решет ?, угол наклона к горизонту линии действия шатуна ?) и режимами работы машины (амплитуда A и частота колебаний ?).
Для обеспечения движения клубней по решетам необходимо, чтобы уравнение (36) стало неравенством, у которого левая часть, зависящая от режимов работы калибровщика стала больше правой, чего можно достичь либо увеличением амплитуды, либо увеличением частоты колебаний. С точки зрения агротребований, предъявляемых к качеству сортирования, увеличение левой части выражения (36) целесообразно осуществлять за счёт увеличения амплитуды, так как повышение частоты колебаний увеличивает силу инерции PJ пропорционально ее квадрату при одновременном уменьшении времени её действия.
Схема силового взаимодействия клубней картофеля с решётной поверхностью (рисунок 9) позволяет решить вопрос об условиях, определяющих характер движения клубней с отрывом и без отрыва от поверхности решета.
| Страницы: | 1 | 2 | 3 | |
Авторефераты по всем темам >>
Авторефераты по техническим наукам