Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии

окальные геолого-динамические факторы формирования комплексных прибрежно-морских россыпей тяжелых минералов

Автореферат докторской диссертации по геологии-минералогии

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

 

Практически все имеющиеся на сегодняшний день формулы для расчета движения наносов, достоверность которых многократно проверена на практике, применяются в условиях субгоризонтального русла и не принимают в расчет наклон дна потока. В реальных условиях прибрежно-морской зоны концентрация тяжелых минералов практически всегда происходит на наклонных поверхностях донных форм рельефа: на волноприбойной поверхности пляжа или грядовых формах в зоне подводных течений сублиторали.

В этом плане наиболее актуальной представляется задача нахождения зависимости минимальной срывающей придонной скорости потока от угла наклона дна к горизонтальной поверхности. С этой целью известные зависимости были адаптированы автором для описания движения рудных и нерудных частиц на локальных участках дна, имеющих существенный наклон к горизонту, но не превышающий угол естественного откоса песчаных осадков в водной среде.

Поток может быть направлен как вверх по склону (набегающая на пляж волна, фронтальный склон донной гряды, тыловой склон гряды при образовании противотока за гребнем, т.н. вальца) (режим 1), так и вниз по склону (скатывающийся обратный ток воды на пляже, тыловой склон гряды без образования противотока) (режим 2).

Составив уравнения баланса сил, действующих на неподвижную частицу в момент перед началом движения на наклонном дне, используя известные соотношения из уравнений гидродинамики и введя в реальные значения расчетных величин (плотности частиц, крупности и т. д.), получаем уравнения минимальных срывающих скоростей для различных режимов движения, углов наклона дна, рудных и нерудных частиц (табл. 2).

Таблица 2.

Минимальные срывающие скорости (v0) для рудных и нерудных частиц на

Рассмотрим процессы, протекающие в возвратно-поступательном потоке в зоне литорали. В зоне забурунивания возникает прибойный поток, который в условиях крутых берегов ударяется о подножие клифа, а на пологих (более характерных для комплексных ПМР) взбегает на пляж, где теряет заметную часть воды на просачивание в толщу осадка, в результате чего обратный поток начинается ближе к урезу и имеет меньшую скорость.

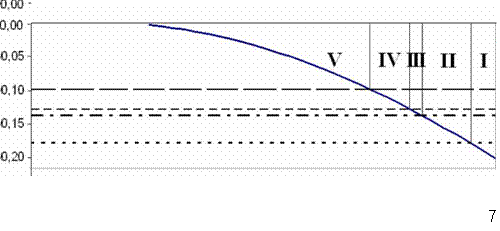
Начало координаты Х расположено на границе зоны заплеска, ось Х ориентирована по нормали к берегу, расстояние до зоны забурунивания Хкр=1. По оси Y откладывается скорость потока, имеющая максимальное значение в зоне забурунивания равное 1. Критические скорости частиц рассчитаны по уравнениям (2.4) - (2.7), уклон пляжа принят постоянным со значением ф=3. Скорость прибойного потока рассчитана по формулам (36, 37) (Проектирование морскиха 1998, прил.3).

0,25 0,20 0,15 0,10 0,05 ">
0,05а 0,1а 0,15а 0,2а 0,25а 0,3а 0,35а 0,4

v |l\ Ш II 1аа 1аа 1 1аа 1аа 1 ............................................................................ J.. 1_____				у
1аа 1
оо о oj^iiioc^oiiciio		-О	*Ч*	о I ?а 1 ООО Х ооолооо

X

От границы забурунивания в сторону пляжа выделяются пять динамических зон (рис.2), различающихся характером перемещения частиц осадка. В зонах II - IV происходит концентрация рудных частиц за счет различных механизмов: II - селективный вынос нерудных частиц, III - отстающая концентрация рудных, IV - селективное выпадение рудных частиц. В зоне V происходит полное выпадение всех частиц из прямого прибойного потока.

Различие прямого и обратного потоков определяется коэффициентом фильтрации осадков пляжа. В силу просачивания воды в осадки пляжа обратный поток начинается с некоторым смещением относительно конца зоны заплеска, и развивается с задержкой относительно значений прямого потока по координате Х. К тому же, минимальная срывающая скорость в условиях набегающей по склону волны больше, чем для скатывающейся.

В результате этого, в наиболее распространенном случае пляжа, сложенного средне-мелкозернистыми песками, с уклоном пляжа от 2 до 5, смещение зон может достигать 0.1-0.2 Хкр, и в зоне концентрации тяжелых минералов обратный поток не достигает значения vr0x. Таким образом, зона образования россыпных концентраций II-IV остается вне области эрозии обратного потока. В этом случае в условиях регулярного ритмичного волнового воздействия происходит образование и накопление повышенных россыпных концентраций тяжелых минералов в одной и той же пляжевой зоне. Содержание тяжелых минералов на пляже может достигать 500-800 кг/м3, как это отмечается на юго-западном побережье Индостана (месторождения Чавара и Манавалакуричи). Из этого также следует, что именно условия волнового воздействия со стабильными параметрами, которым наиболее соответствует волнение типа океанской зыби, создают оптимальные условия для концентрации тяжелых минералов. В случае нерегулярного штормового воздействия, при котором волнение ветровой природы имеет неустановившиеся характеристики, крупных россыпных тел с высокими концентрациями полезного компонента не возникает.

Образование повышенных россыпных концентраций в зоне мелководья имеет иной механизм. Существенная асимметрия волновых движений появляется только в зоне забурунивания, и поэтому волновое воздействие на дно в зоне мелководья не приводит к концентрированию тяжелых минералов. При этом вдольбереговые течения ветроволновой природы могут достигать величин, достаточных для массового перемещения мелкопесчаного материала и в условиях грядовой формы движения наносов приводить к образованию значительных россыпных концентраций.

Анализ литодинамики на различных участках подводных гряд с разными значениями угла наклона поверхности относительно направления потока показывает, что по мере увеличения скорости потока более vx>v0x на фронтальном склоне гряды начинается движение

нерудных частиц вверх по склону, при этом у подножия начинается образовываться остаточная россыпная концентрация.

При vx>vr0x приходят в движение по поверхности частицы тяжелых минералов, а при vx>v0z> vr0z нерудные и рудные частицы соответственно переходят в режим сальтации и взвеси. На тыловом склоне гряды образуется т.н. валец, где придонное течение направлено вверх по склону в направлении, противоположном общему потоку.

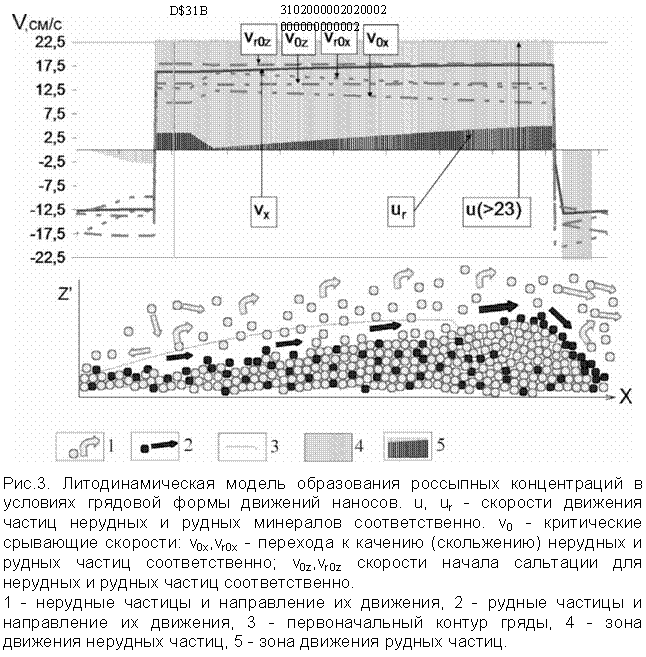
На рис.3. смоделирована ситуация, при которой на всем лобовом склоне гряды нерудные частицы начинают движение взвешиванием, а рудные - качением. Кроме того, нерудные частицы начинают движение взвешиванием в верхней части тылового ската при одновременном скатывании и аккумуляции рудных частиц на этом участке. Нерудные частицы, выпадающие из взвеси в подвалье гряды, движутся к ее тыловому скату, где переходят во взвешенное состояние, не снижая, таким образом, концентрации рудных частиц. Взвешенные нерудные частицы, достигшие лобового склона следующей гряды, продолжают движение в положительном направлении взвешиванием. Процесс сепарации рудных и нерудных частиц на этой стадии представляется наиболее эффективным, в тыловой зоне гряды начинается интенсивное концентрирование тяжелых рудных минералов.

Надо отметить, что при vx>vr0z все частицы переходят в взвешенное состояние, образованные россыпные концентрации разрушаются и, таким образом, для осадков, состоящих из нерудных частиц диаметром 0.1 мм и плотностью 2.6 г/см3 и рудных диаметром 0.067 мм и плотностью 4.6 г/см3 россыпеобразование происходит только в условиях оптимума придонных скоростей (приведенных к горизонтальной поверхности дна) в пределах 9.8-17.9 см/с.

Эти два механизма образования россыпных концентраций (волноприбойный литоральный и грядовый мелководный) приводят к формированию описанных выше неоднородностей в пределах комплексных ПМР. В ископаемых россыпях России отмечается преобладание сублиторальных мелководных фаций. В определенной мере это объясняется тем, что при наиболее благоприятном для россыпеобразования регрессивном режиме развития палеобассейна в первую очередь попадают в зону эрозии и разрушаются пляжевые россыпи. Несомненно, что этот эрозионно-тектонический фактор в определенной мере объясняет особенности палеороссыпей России, но нам представляется, что существует и второй (палеогидродинамический) фактор, который определяется особенностями гидродинамики и волнового режима палеобассейнов, существовавших на территории России.

В силу палеогеографического положения на территории ВосточнонЕвропейской и Западно-Сибирской мегапровинций преобладали мелководные замкнутые или существенно ограниченные от мирового океана бассейны россыпеобразования (мелководные континентальные внутренние и окраинные моря мезозоя Русской платформы, олигоценовое Мансийское озеро-море на территории Западной Сибири, миоценовое Сарматское море, занимавшее территорию предкавказского прогиба и Днепровско-Донецкой впадины и т.д.). Гидродинамика и волновой режим этих бассейнов не были благоприятны для существования устойчивых режимов волнения типа зыби, которые играют основную роль при формировании россыпей литорального типа.

В то же время, ветроволновое воздействие в условиях мелководного моря способствует образованию устойчивых придонных течений, достаточно интенсивных для перемещения осадков песчаной размерности в грядовом режиме, что изначально определяет преобладание россыпей мелководного типа над литоральными.

Глава 3. Моделирование вдольберегового потока наносов и влияние литодинамических режимов на процессы концентрирования тяжелых минералов

В главе 3 раскрывается второе защищаемое положение диссертации.

Структура потока россыпеобразующих наносов находит отражение в параметрах образующихся россыпных объектов, поэтому моделирование потока наносов и поведения в нем россыпеобразующих компонентов позволяет исследовать и формализовать литодинамический фактор образования комплексных ПМР.

Для создания применимой на практике модели был использован метод баланса масс, хорошо зарекомендовавший себя при моделировании вторичных ореолов и потоков рассеяния на суше (Поликарпочкин, 1976). Принятая за основу модели схема миграции вещества выглядит следующим образом: поступление с берега в активную зону обломочного материала на участке абразии; перенос его вдольбереговым потоком в зоне транзита и селективное выпадение из потока в зоне аккумуляции. Локализация разнородных литодинамических зон и ширина активной зоны потока контролируется соотношением мощности и емкости потока наносов.

vHY+

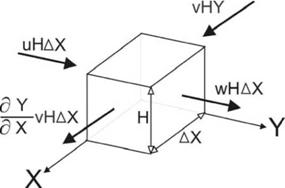
Для составления исходных дифференциальных уравнений баланса масс в активной зоне в ней выбрана элементарная ячейка высотой Н, длиной ЛХ (по оси ОХ, направленной от начала устойчивого потока вдоль берега в направлении результирующего перемещения наносов) и шириной Y. Последняя величина по своему физическому смыслу соответствует ширине активной зоны потока. С(Х) - содержание рудного вещества в потоке в точке Х.

Рис. 4. Схема составления уравнения баланса масс.

На участке абразии поступление материала с суши происходит через сечение НЛХ со скоростью u, количество наносов (в объемных единицах), привносимое в ячейку вдольбереговым потоком в единицу времени vHY, где v - скорость переноса. Через нижнюю по оси Х

стенку из ячейки в единицу времени выходит vHY + ^/дХ^НДХ вещества, а через дальнее от берега боковое сечение \л/НДХ, где w -скорость удаления материала из активной зоны в сторону акватории (рис.4). Последний параметр различен для нерудного (w) и рудного (wr) материала.

Обозначим участок поступления в поток тяжелых минералов Х0Х1, длину участка абразии Х0Х', зоны транзита наносов Х'Х", зоны аккумуляции Х"Хтах. Сг - среднее содержание тяжелых рудных материалов в поступающих в активную зону образованиях.

Заменим реальный пульсирующий во времени вдольбереговой поток наносов лидеальным установившимся, с неизменными во времени параметрами миграции вещества через ячейку (дС/dt = 0). Допустим также, что все параметры кроме концентрации тяжелых (рудных) минералов С и ширины активной зоны наносов Y постоянны на всем протяжении участка. Тогда приравняв нулю разность объемов материала поступающего в единицу времени в ячейку и выходящего из нее и поделив полученное выражение на постоянные величины Н и ЛХ, на участке абразии получим для всего мигрирующего материала:

(dY/ dX)V + w - u = 0 (3.1)

Для рудного материала на участке поступления материала в поток Х0Х1 полученное дифференциальное имеет форму:

(^Y/ dX)V + Слг -а = 0 (3.2)

Ниже по вдольбереговому потоку наносов где не происходит подпитка потока рудным веществом (Х > Х1):

(XY/ dX)V + Слг = 0аа (3.3)

Решая составленные дифференциальные уравнения для участка абразии, получаем для зоны источника Х0Х1 (Лаломов 1991, 1992):

С(х)=КСг(Ха-Х0а)/ Ха (3.4)

где:аа К = u/(u-w+wr)аа (3.5)

A = (u-w+wr) / (u-w)аа (3.6)

На участке абразии ниже по потоку от источника Х1 <Х< Х':

С(х)=С(х1 )(Х1 / Х)а (3.7)

где С(х1) - содержание тяжелых минералов в потоке на нижней границе источника Х=Х1.

В зоне транзита наносов Х'Х" отсутствует поступление материала в поток с суши (u=0); вследствие перемыва отложений глинистые фракции оказываются вынесены из вдольберегового потока и, следовательно, w весьма незначительно, в результате чего получаем:

С(х) * С(*) * constа (3.8)

То есть на участках стационарного вдольберегового потока наносов, где отсутствуют абразия берега или аккумуляция материала содержание тяжелых минералов в первом приближении остается величиной постоянной.

На участке аккумуляции (Х>Х") в исходную схему необходимо ввести величину скорости выпадения материала из потока наносов; для безрудного и рудного материала она будет обозначаться U и Ur соответственно. При этом, как и для зоны транзита, u=0, w=0; рудный материал отлагается в зоне россыпеобразования вместе с безрудным, и, следовательно, его безвозвратным уходом из зоны россыпи можно пренебречь (wr=0). После выпадения всего материала в зоне аккумуляции в точке Xmax вдольбереговой поток наносов оканчивается.

Протяженность участка аккумуляции (Xmax - X") определяется фактической емкостью потока наносов и скоростью выпадения безрудного материала из потока. Емкость потока (Е), формирующегося на участке абразии, определяется как произведение реального поступления материала в поток (поступление материала с берега за вычетом выноса тонких фракций на акваторию бассейна равное u-w) на протяженность участка абразии (X'). По мере выпадения материала из потока со скоростью U емкость потока будет уменьшаться и стремиться к нулю в точке Xmax.

Таким образом, протяженность участка аккумуляции равна:

Xmax - X" = Е/U = (u-w)X'/ U,аа (3.9)

Принимая во внимание все указанные выше условия, составляя и решая уравнения, аналогичные (3.1) - (3.7) и учитывая скорость выпадения из потока рудного материала, получаем уравнение:

С(Х) = С(Х") (( Xmax - X)/(Xmax - X"))(1-Br) ,а (3.10),

где Br = Ur/ U.

Проверка адекватность предлагаемой модели была осуществлена на ряде современных и ископаемых россыпей (рис.5). Для масштабирования разноразмерных данных длина россыпей указана в процентах от начала россыпепроявления по вдольбереговому потоку, средние содержания по сечениям россыпи - в процентах от суммы содержаний по россыпи, принимая сумму содержаний равной 100%. Данные по пяти исследованным россыпям были осреднены. Результаты моделирования даны в условных единицах при Х0=0, Х1=20 %, X' и X" равны 40 % и 60 % соответственно, Xmax=100 %, Cr=1, К=10, А=1.5,

Br=1.67.

Для четырех объектов коэффициент корреляции (Кк) между природными и модельными данными изменяется в пределах от 0.78 до 0.94, (критическое значение при однопроцентном уровне значимости равно 0.71), что говорит о высоком уровне сходимости фактических и модельных данных на всем протяжении шлейфа тяжелых минералов.

Исключение составили данные по россыпи Чавара (Кк = 0.46), что свидетельствует об ином механизме образования этой россыпи. Возможно, причина в том, что поступление обломочного материала в береговой поток на этом участке происходит не за счет абразии или речного стока, а в результате выноса материала с подводного берегового склона (Патык-Кара, 2007), что не учитывается в построенной модели.

5 зо и

>ч

о"

Рис. 5. Проверка адекватности модели баланса масс. 1 - Fingal Point-Cudgen Head, South Wales, Australia (Gardner, 1955), 2 - Eastern Eucla Basin, South Australia (Hou, 2008), 3 - Chavara placer deposit, India (Babu, 2007), 4 - россыпь участка Мансийский ХМАО (авторские материалы), 5 - кембро-ордовикские песчаники северо-запада Русской платформы (авторские материалы), 6 -усредненная кривая по россыпям 1-5, 7 - результаты моделирования.

СКАЧАТЬ ОРИГИНАЛ ДОКУМЕНТА

Страницы: | 1 | 2 | 3 | 4 | 5 | 6 |

     Авторефераты по всем темам  >>  Авторефераты по геологии-минералогии