Самаркандский Государственный
| Вид материала | Документы |
- Кубанский государственный аграрный университет кубанский государственный технологический, 51.16kb.
- Темы рефератов дисциплина «протокол», 27.15kb.
- Осрб 1-36 04 02-2008, 702.53kb.
- "Философские науки", 789.13kb.
- Р. Х. Колоев 2009 г. Реестровый номер торгов 091005/893143/1037 конкурс, 1101.53kb.
- Все о корее краткий обзор, 616.58kb.
- Государственная символика республики беларусь государственный флаг Республики Беларусь, 68.33kb.
- Государственный стандарт союза сср соединения сварные методы контроля качества гост, 157.81kb.
- Государственный сектор: институциональные направления развития в российской экономике, 389.44kb.
- Программа VI конгресса «юпитер 2011», 129.66kb.
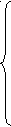
(5)
Методов решения системы (5) очень много. Среди них наиболее удобным и экономичным является метод квадратного корня. Вместе с тем можно пользоваться методом Гауса.
ln b0 = b0'
b0 = e b0'
Решая (5), находим неизвестные коэффициенты регрессии (b0', b1, b2, … bm). Подставляя их в формулу (1), получим конкретную производственную функцию. Адекватность построенной функции проверяется при помощи статистики Фишера:
ПРИМЕЧАНИЕ
Систему (5) можно представить в следующем матричном виде:
V'VB = V'U (5)
г
| | 1 | V11 | V12 | … | V1m | | b0 | | U1 |
V= | 1 | V21 | V22 | … | V2m | ; B= | b1 | ; U= | U2 |
| . | . | . | … | . | . | . | |||
| . | . | . | … | . | . | . | |||
| . | . | . | … | . | . | . | |||
| | 1 | Vm1 | Vn2 | … | Vnm | | bm | | Un |
де
V' – транспонированная матрица.
Ax = b a11x1 + a12x2 +…+ a1mxm = a1,m+1
a21x1 + a22x2 +…+ a2mxm = a2,m+1
| | a11 | … | a1m | | b1 |
| A = | … | … | … | ; b = | … |
| | am1 | … | amm | | bm |
| | | | | | |
| | a11 | … | a1,m+1 | | |
| A = | … | … | … | | |
| | am1 | … | am,m+1 | | |
. . . . . . . . . . . . . . . . . . . . . . . . . .
am1x1 + am2x2 +…+ ammxm = am,m+1

LABEL 3, 4, 5, 6;
const n=5, m=2, m1=3, m2=4;
VAR
Y, U : ARRAY [1…n] of real;
X : ARRAY [1…n, 1…m] of real;
V : ARRAY [1…n, 1…m1] of real;
B : ARRAY [1…m1] of real;
A : ARRAY [1…m1, 1…m2] of real;
I, J, K, L : INTEGER;
S, T1, F : REAL;
BEGIN
WRITELN ('Введите значения X и Y');
FOR I : = 1 TO N DO
BEGIN
READLN (Y[I]); U[I] : = LN (Y[I]); V[I, 1] : =1;
FOR J : =1 TO M DO
BEGIN
READ (X[I, J]); V[I, J+1] : = ln (X[I, J])
END
END;
FOR I : = 1 TO m1 DO
BEGIN
FOR J : = I TO M1 DO
BEGIN
A[I, J] : = 0;
FOR K : = 1 TO N DO
A[I, J] : = А[I, J] + V[K, I] * V[K, J];
A[I, J] : = А [I, J]
END;
A[I, M2] : = 0
FOR K : = 1 TO N DO
A[I, M2] : = A[I, M2] + V[K, I] * U[k]
END;
P : =0;
3 : P : = P+1;
FOR K : = P TO m1 DO
IF A [K, P] <>0 THEN go to 4;
go to 5;
4 : IF K=P THEN go to 6;
for L : = p TO m2 DO
BEGIN
T1 : = A [P, L];
A[P, L] : = A [K, L];
A[K, L] : = T1;
END;
6: for j : = M2 down to p do
BEGIN
A[P, J] : = A[P, J] / A[P, P]
END;
FOR I ; = K+1 TO m1 DO
FOR J ; =P+1 TO m2 DO
BEGIN
A[I, J] : = A[I, J] - A[I, P] * A[P, J]
END;
IF P <>m1 THEN go to 3;
WRITELN ('решение системы:');
FOR I: m1 down to 1 DO
BEGIN
B[I] : = A [I, m2]/A[I, I];
WRITELN ('B,' I:1, 'J =', B [I] : 9 : 2)
END
5:END.
