Самаркандский Государственный

Вид материала

Содержание

Статические межотраслевые модели
Y сразу определить валовые выпуски X
В называется матрицей полных затрат, а ее элементы b
R - общее число рабочих (трудовых ресурсов); μ
U = C∙Y→max

Подобный материал:

1 2 3 4 5 6 7

Для каждой i-той отрасли в балансе соответствует i-тая строка и i-тый столбец. Матрица элементов стоящих на пересечении первых n+1 строк и n+1 столбцов называется первым разделом МБ. Это важнейшая часть МБ, поскольку именно в ней содержится информация о межотраслевых связях.

Э

лемент x_ij (i=1,n; j=1,n) показывает производственный затраты j-той отраслью продукции i-той отрасли за год, т.е. характеризует межотраслевые поставки сырья, материалов, топлива от i-того к j-той отрасли, обусловленные производственной деятельности отраслей производства.

В n+1 столбце первого раздела записаны суммы величин x_ij по строкам, и в n+1 строке раздела записываются суммы величин x_ij по столбцам. Суммы, записанные n+1 столбце характеризуют сумму всех поставок i-той отрасли другим отраслям, которая называется производственным потреблением. Величины, записанные n+1 строке характеризуют производственные затраты j-той отрасли.

Величина, записанная на пересечении n+1 строки и n+1 столбца характеризуют сумму всех производственных затрат всех отраслей или же сумму производственного потребления продукции всех отраслей. Она называется (∑∑X_ij) промежуточным продуктом народного хозяйства.

Второй раздел МБ состоит из матрицы элементов, стоящих на пересечении n+1 первых строк и (n+2) и (n+3) столбцов МБ. Первый столбец этого раздела называется столбцом конечного потребления продукции отраслей, под которым понимаются личное и общественной потребление, не идущее на текущее производственной потребление. Сюда включаются накопление и возмещение выбытия основных фондов, прирост запасов, личное потребление населения, бюджетные расходы. Кроме того в конечный продукт входит сальдо экспорта и импорта продукции. В нашей таблице конечное потребление продукции i-той продукции обозначено через Y_i. Обычно в Мб конечный продукт рассматривается более подробно. Второй столбец второго раздела называется столбцом валовых продуктов отраслей, который определяется следующим образом:

X_i=∑ X_ij+ Y_i,(i=1,n)

j=1

В n+1 строке второго раздела стоят величины, ∑Y_i и ∑X_i , которые характеризуют соответственно суммарный конечный продукт народного хозяйства и суммарную валовую продукцию.

Третий раздел расположен под первым и отражает структуру валового продукта отраслей. В нашей таблице она состоит из двух строк. В первой из них стоят величины V_j, каждая из которых означает условно-чистую продукцию отрасли. Условно-чистая продукция отрасли равна разнице между валовой продукцией X_jи производственными j-той отрасли

∑ X_ij

i=1

Математически это можно записать

_j =X_j- ∑ X_ij,(j=1,n)

i=1

Обычно в МБ условно-чистая продукция каждой отрасли разделяется на амортизационные отчисления и чистую продукцию отрасли, в которую включаются заработная плата, прибыль и т.д.

Следует отметить, что верно следующее соотношение:

n		n
∑ Y_i	=	∑ V_j
i=1		j=1

СТАТИЧЕСКИЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ

Обычно межотраслевая модель строится в следующих предпосылках:

В каждой отрасли имеется единственная технология производства
Нормы производственных затрат зависят от объема выпускаемой продукции
Не допускается замещение в производстве одних видов продукции другими.

ри этих предпосылках величину X_ijможно представить в следующем виде:

X_ij=a_ij · X_j (i, j = 1, n) (1)

Величину a_ij называют коэффициентом прямых затрат, который показывает, какое количество продукта i-той отрасли надо затратить на производство единицы продукции j-той отрасли. Эти коэффициенты считаются постоянными величинами в межотраслевых моделях. Соотношение (1) определяет функцию затрат для отрасли. Она дает возможность по выпуску X_j продукции j-той отрасли на основе технологических коэффициентов a_ij определить затраты X_ij. Если соотношение (1) поставим в баланс продукции:

X_i=∑ X_ij+Y_i

j=1

то получим следующее соотношение:

n
X_i=∑ a_ij X_j+Y_i	(2)
j=1

Последнее удобно записывать в матричной форме:

X = Ax + y (3)

где x – вектор столбец x = (x₁, x₂, …, x_n)'

y – вектор столбец y = (y₁, y₂, …, y_n)'

A = (	a_n, …, a_1n	)
	a_n1, …, a_nn

Матрицу А принято называть матрицей прямых затрат, а соотношение (3) – балансом распределения продукции. Оно является основным соотношением в межотраслевой модели. Возникает вопрос: как построить матрицу А? Имеются два основных метода:

Статистический, в котором коэффициенты определяются на основе анализа отчетных балансов за предыдущие годы
Нормативный, в котором a_ij определяется по нормативам затрат

Если матрица А построена то соотношение (3) можно использовать для анализа и планирования народного хозяйства. Действительно, если задать конечный продукт Y, то валовой выпуск X определяется из соотношения:

(E - A)X = Y

где Е - единичная матрица.

Из последнего можно получить следующее:

X = (E - A)^-1·Y (4)

Таким образом, баланс распределения продукции дает возможность по конечному выпуску Y сразу определить валовые выпуски X. В этом заложена основная идея использования межотраслевых моделей для планирования производства. Прежде чем переходить к использованию соотношения (4), необходимо выяснить:

Всегда ли существует обратная матрица: (E - A)^-1
Не получим ли в некоторых случаях отрицательные значения валовых выпусков.

Вместе с тем в теории матриц доказано, что такая обратная матрица существует и ее элементы неотрицательны, если выполняются следующие условия:

a_ij ≥ 0 (i, j = 1, n) (5)

n
∑ a_ij <1 (j =1, n)	(6)
i=1

Соотношение (5) вытекает из не отрицательности величины x_ij и положительности валовых выпусков отрасли x_j. Соотношение (6) можно получить из следующего соотношения:

X_j=∑ X_ij+V_j

i=1

Так как

V_j > 0, X_j> ∑ X_ij

i=1

Подставляя в это соотношение формулу (1) получим следующее:

X_j>∑ a_ij·x_j

i=1

Из последнего получаем выполнение условия (6). Если обратную матрицу (E - A)^-1обозначим через В, то соотношение (4) получит вид:

X = BY (7)

М

атрица В называется матрицей полных затрат, а ее элементы b_ij, (i, j = 1, n)называются коэффициентами полных затрат. Этот коэффициент показывает, каким должен быть валовой выпуск i-той отрасли, для того чтобы обеспечить выпуск единицы конечного продукта j- той отрасли. Между коэффициентами a_ij и b_ij верно следующее соотношение:

a_ij ≤ b_ij(i, j = 1, n) (8)

Последнее соотношение основывается на следующем:

B = E + A + A² + A³ + A⁴ + … (9)

Докажем это соотношение: умножим левые и правые части соотношения (9) на (E - A) и получим :

(E - A)·B = (E – A)(E + A+ A² + A³ + A⁴ + … )

E = E + A + A² + A³ + … - A – A² – A³ - …

E = E

Таким образом значение матрицы В дает возможность на основе соотношения (7) по конечному продукту определять валовые выпуски отрасли, а затем по ним и матрице А строить плановый межотраслевой баланс по формуле (1). Такая математическая модель дает возможность проводить вариантные расчеты плановых межотраслевых балансов и выбрать из них наилучший, т.е. решать оптиматизационную задачу. Одну из многочисленных задач можно сформулировать следующим образом: надо найти такие неотрицательные варианты конечного продукта Y и валовых выпусков X , чтобы на них достигался максимум критерия (10)

n
U =∑ C_iY_i→ max	(10)
i=1

при выполнение следующих условий

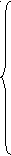
n
X_i=∑ X_ij+Y_j;
j=1
X_i ≤ μ_iK_i;
n	X_i υ_i	≤ R
∑
i=1

этой модели C_i, (i=1, n) положительные коэффициенты, характеризующие важность соответствия конечных продуктов;

K_i - основные фонды i-той отрасли;

R - общее число рабочих (трудовых ресурсов);

μ_i-коэффициент фонда отдачи i-той отрасли;

υ_i - производительность труда i-той отрасли.

Э

U = C∙Y→max

X = Ax + Y

X ≤ K∙μ

P∙x ≤ R

та задача может быть записана в следующей матричной форме:

где

С= (С₁, C₂, …, C_n);
μK = (μ₁K₁, μ₂K₂, …, μ_nK_n);
Р = (	1 υ₁	,	1 υ₂	, … ,	1 υ_n	)

Эта задача является задачей ЛП.

Рассмотрим сильно упрощенное четырехсекторное описание экономики, в котором выделены 2 отрасли (сельское хозяйство и промышленность), один первичный фактор производства (труд) и государственный сектор, который потребляет продукции обеих отраслей и использует труд. В этом примере государственный сектор ничего не производит для экономики и его потребление представляет спрос на товары, производимые в секторах.

Д

Производ. сектор	Потребляющий сектор				В с е г о
Производ. сектор	с/хоз-во	пром-ть	трудовые ресрусы	конеч.спрос (гос.сектор)	В с е г о
С/хозяйство (т)	600	400	1400	600	3000	Х₁
Промышленность (машин)	1500	800	700	1000	4000	Х₂
Трудовые ресурсы (число занятых)	900	3800	700	600	6000	Х₃

					X_j
	X_ij				X_j

опустим, что в результате наблюдения за натуральными потоками продукции между 4-мя секторами экономики на протяжении некоторого периода имеем следующую таблицу «Затраты и выпуск» (межотраслевого баланса).

М

ожно ожидать, что процесс производства, отражаемый этой таблицей, изменится, если применить усовершенствованную технологию или изменить относительные цены трех факторов производства. Однако, допустим, что цены относительно стабильны и технология меняется медленно. Кроме того, предположим, что государственный сектор предполагает теперь потребить 1000 т продукции сельского хозяйства, 1200 машин, и ему потребуется нанять 800 человек в следующем периоде. Учитывая, что в рассматриваемом случае эти потребности государства представляют собой конечный спрос, требуется определить, каковы должны бать трудовые ресурсы и уровни выпуска в каждом производственном секторе. Иначе говоря, определим, каковым будет X, если Y=(1000,1200,800).

X

X_m=	600	400	1400
	1500	800	700
	900	4800	700

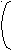
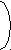
E =	1	0	0
	0	1	0
	0	0	1

_ij

X_ij = a_ij ∙ X_j

	600 3000	400 4000	1400 7000		0,2	0,1	0,2
A =	1500 3000	800 4000	700 7000	=	0,5	0,2	0,1
	900 3000	4800 4000	700 7000		0,3	1,2	0,1

a_ij=

X_ij

X_j

(i, j = 1, 3)

	1 0,264	0,6	0,33	0,17
B =		0,48	0,66	0,18
		0,84	0,99	0,59

= (E - A) ^-1

X = BY

П

	1 0,264	0,6	0,33	0,17		1000		4288
X=BY=		0,48	0,66	0,18	∙	1200	≈	5364
		0,84	0,99	0,59		800		9470

еред тем, как использовать матрицу В, ее проверяют при помощи соотношения: X=BY. Проверка показывает, что матрица В построена правильно. Используя матрицу В, вычислим:

Таким образом, для удовлетворения нового конечного спроса в следующем периоде необходимо будет произвести приблизительно 4288 т сельскохозяйственной продукции; 5364 машин; для чего потребуется 9470 работников.

Задача.

Пусть все отрасли производства товаров и услуг объединены в два сектора:

1 – производство товара для пользования;

2 – производство товаров кратковременного пользования.

Каждый сектор производит продукцию для другого сектора и для конечного потребления. Допустим, что мы располагаем следующими данными о сбыте

(млрд. сум)

Поставщик	Покупатель
Поставщик	произ. товаров для пользования	произ.товаров кратко-срочного пользования	потребители
Производство товаров для пользования	24	90	6	}120
Производство товаров краткосрочного пользования	12	45	93	}150

К

X_m=

24

90

12

45

ij = (1,2)

A =

24

120

90

150

=

0,2

0,6

E =

1

0

12

120

45

150

0,1

0,3

0

1

аков общий объем сбыта

П
B = E + A + A²

A²=	(	0,2	0,6	)∙ (	0,2	0,6	)= (	0,2∙0,2+0,6∙0,1	0,2∙0,6+0,6∙0,3	)= (	0,1	0,3	)
A²=	(	0,1	0,3	)∙ (	0,1	0,3	)= (	0,1∙0,2+0,3∙0,1	0,1∙0,6+0,3∙0,3	)= (	0,05	0,15	)

В =	(	1	0	)+(	0,2	0,6	)+ (	0,1	0,3	)= (	1,3	0,9	)
В =	(	0	1	)+(	0,1	0,3	)+ (	0,05	0,15	)= (	0,15	1,45	)

ример:

Рассмотрим данные, относящиеся к стальной компании, охватывающей шахты по добыче угля и руды, печи с форсированным дутьем производящие слитки и прокатные станы, выпускающие стальные листы. Предположим, что следующая матрица коэффициентов «затраты – выпуск», точно характеризует соответствующие производственные процессы.

Виды потребляемых материалов	Выпускаемая продукция
Виды потребляемых материалов	Уголь (т)	Руда (т)	Слитки	Стальные листы
Уголь	0,1	0,1	0,5	0,1
Руда	0,0	0,0	1,0	0,0
Слитки	0,0	0,0	0,0	1,0
Стальные листы	0,0	0,0	0,0	0,0

Допустим, что фирме желательно сбыть остальной части экономики, в которой она функционирует, 3000 т угля, 6000 слитков и 12000 стальных листов, идущих в производственное потребление. Требуется определить, сколько каждого вида продукции надо произвести.

Решение.

Y

	0,1	0,1	0,5	0,1		1	0	0	0
A =	0,0	0,0	1,0	0,0	Е =	0	1	0	0
A =	0,0	0,0	0,0	1,0	Е =	0	0	1	0
	0,0	0,0	0,0	0,0		0	0	0	1

=(3000; 0,6000; 12000) i, j = (1,4)

	0,01	0,01	0,15	0,51
А² =	0	0	0	1
А² =	0	0	0	0
	0	0	0	0

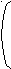
В = Е + А + А²

	1	0	0	0		0,1	0,1	0,5	0,1		0,01	0,01	0,15	0,51
В=	0	1	0	0	+	0	0	1	0	+	0	0	0	1	=
В=	0	0	1	0	+	0	0	0	1	+	0	0	0	0	=
	0	0	0	1		0	0	0	0		0	0	0	0

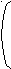
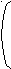
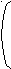
	1,11	0,11	0,65	0,61
=	0	1	1	1
=	0	0	1	1
	0	0	0	1

П
X=BY

	1,11	0,11	0,65	0,61		3000		14550
Х=	0	1	1	1	∙	0	=	18000
Х=	0	0	1	1	∙	6000	=	18000
	0	0	0	1		12000		12000

рограмма вычисления Х

const n=4

VAR I, J, K: INTEGER; см: REAL;

А: ARRAY [1..n, 1..n] OF REAL;

Y: ARRAY [1..n] OF REAL;

X: ARRAY [1..n] OF REAL;

B: ARRAY [1..n, 1..n] OF REAL;

C: ARRAY [1..n, 1..n] OF REAL;

BEGIN

FOR I : = 1 TO N do

BEGIN READ (Y[I]);

FOR J : = 1 TO N do begin

READ (A[I,J]); C[I,J] : = A[I,J] end

end;

FOR I: = 1 TO N do

BEGIN B [I,J] : =A [I,I] +1;

FOR J : =1 TO N do

If i<>j THEN b [i, j] : = a [i, j]

END;

M1: for i: =1 TO n do begin

for j: =1 TO n do

begin x [j]: =0

for k: =1 TO n do

X [j]: =x[j]+C[i,k]∙Q[k,j];

END;

For j: =1 TO n do C [i, j]: =x[j]

END;

CM: =C[1,1];

For i: =1 to n do

For j: =1 to n do

Begin B [i, j]: = B [i, j] + C [i, j];

If C [i, j] >CM then CM: = C [i, j]

END;

If CM >0,001 then go to M1;

For i:=1 TO N do

For j:=1 TO N do

WRITE (B[i, j]:7:2);

END;

END.

Матрица С = А²+ А³+ … называется матрицей косвенных затрат.

A =	24 120	90 150	=	0,2	0,6	E =	1	0
A =	12 120	45 150	=	0,1	0,3	E =	0	1

Blog

Самаркандский Государственный

Содержание