2. Кинематика теории относительности. Энергия и импульс
Преобразования Лоренца. Формула, описывающая распространение фронта сферической световой волны, может быть переписана в виде:

Введем обозначение:
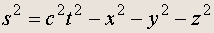
Величина s 2 называется интервалом. Тогда уравнение распространения световой волны примет вид: s 2 = 0 .
Из геометрических соображений очевидно, что в областях абсолютного прошлого и абсолютного будущего (иначе их называют времениподобными областями) s 2 > 0 , а в пространственноподобной области s 2 < 0 . Поскольку скорость света не зависит от выбора ИСО, то разделение всех событий по отношению к данному на те, которые лежат во времениподобной или пространственноподобной областях, не
зависит от системы отсчета. Другими словами, интервал s инвариантен относительно перехода из одной ИСО в другую. Согласно принципу относительности, уравнение s 2 = 0 , выражающее физический закон распространения света, обязано иметь один и тот же вид во всех ИСО.
Легко убедиться простой подстановкой, что величина s2 не сохраняет своего вида при преобразованиях Галилея. Отсюда мы приходим к выводу о необходимости существования иных преобразований координат и времени при переходе от одной ИСО к другой. При этом, учитывая относительный характер одновременности, уже нельзя считать t' = t , т.е. считать время абсолютным, идущим независимо от наблюдателя, и вообще отделить время от пространства, как это можно было сделать в ньютоновской механике.
Преобразования координат и времени события, не меняющие величины интервала s 2 , носят название преобразований Лоренца. Их вывод выходит за рамки школьной программы. Поэтому ограничимся проверкой того, что выписанные ниже преобразования действительно сохраняют величину интервала.
Преобразования Лоренца имеют вид:
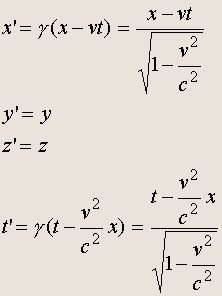 (2.1)
(2.1)
Здесь v - скорость движения одной ИСО относительно другой, величина

носит название лоренц-фактора и, как легко видеть, может меняться от 1 до Ґ при изменении скорости v от 0 до c .
Преобразования Лоренца удобно переписать, введя вместо времени t другую величину: x 0 = ct , имеющую размерность длины, и обозначив x = x 1 , y = x 2 , z = x 3 . Тогда, умножая четвертое равенство на c справа и слева и вводя обозначения

получим:
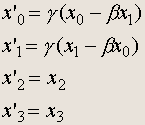 (2.2)
(2.2)
Теперь нетрудно проверить инвариантность интервала, который в новых обозначениях принимает вид:

Имеем:
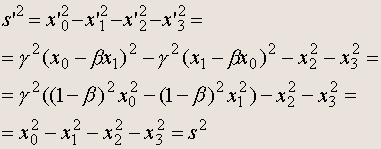
что и требовалось доказать.
Часы и линейки. Наиболее парадоксальными непосредственными следствиями преобразований Лоренца являются утверждения, что наблюдатели в двух разных ИСО будут получать разные результаты при измерении длины какого-то стержня или интервала времени между двумя событиями, произошедшими в одном месте.
1. Сокращение размеров. Пусть стержень расположен вдоль оси x' системы отсчета К' и покоится в этой
системе. Его длина l' = x' 2 - x' 1 фиксируется наблюдателем в этой системе. Переходя в неподвижную систему К , можем записать выражения для координат конца и начала стержня, измеренных в один и тот же момент времени по часам неподвижного наблюдателя:
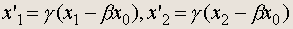
Отсюда:

Эту формулу обычно записывают в виде:
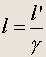 (2.3)
(2.3)
Так как g>1 , то это означает, что длина стержня l в "неподвижной" системе отсчета оказывается меньше длины этого же стержня l' в движущейся системе ( лоренцовское сокращение длины ).
2. Замедление темпа хода времени. Пусть два события происходят в одном и том же месте в системе К' и интервал времени между этими событиями по часам наблюдателя, покоящегося в этой системе, равен
Dt = t' 2 - t' 1 .
Принято называть время t , измеренное по часам покоящегося наблюдателя, собственным временем . Мы
хотим найти связь между собственным временем и временем, измеренным по часам движущегося наблюдателя. Так как
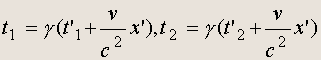
где x' - неизменная пространственная координата события, то, вычитая одно равенство из другого, находим:
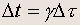 (2.4)
(2.4)
Из этой формулы следует, что часы в системе К показывают больший интервал времени между двумя событиями, чем часы в системе К' , движущейся относительно К . Иными словами, интервал собственного времени, который показывают часы, движущиеся вместе с наблюдателем, всегда
меньше интервала времени, который показывают часы неподвижного наблюдателя.
Сложение скоростей. Запишем преобразования Лоренца для изменения координат тела D x, D y, D z за промежуток времени D t . Имеем:
 (2.5)
(2.5)
Здесь V - направленная вдоль оси x скорость движения одной системы относительно другой.
Скорость тела в лабораторной системе v = D r/ D t , а скорость этого же тела в системе, движущейся вдоль оси x со скоростью V относительно лабораторной системы, равна v' = D r'/ D t' . Поэтому
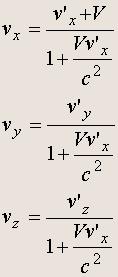 (2.6)
(2.6)
В предельном случае, когда все скорости много меньше скорости света, V << c v' << c (нерелятивистский случай), можно пренебречь в знаменателе вторым слагаемым. Тогда приходим к закону сложения скоростей классической механики: v = v' + V .
В противоположном, релятивистском случае (скорости близки к скорости света) легко убедиться, что, вопреки наивному представлению, при сложении скоростей невозможно получить скорость, превышающую скорость света в вакууме. Пусть, например, все скорости направлены вдоль оси x v' = c , тогда видно, что и v = c .
Соотношение Эйнштейна. Главной прикладной формулой ЧТО является установленное А. Эйнштейном соотношение между энергией E , импульсом p и массой m свободно движущейся частицы:
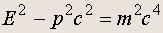
Эта формула заменяет ньютоновскую формулу, связывающую кинетическую энергию с импульсом:
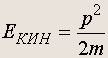
Из нее следует, что при p = 0
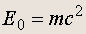 (2.7)
(2.7)
Смысл этой знаменитой формулы в том, что массивная частица в сопутствующей системе отсчета (т.е. в ИСО, движущейся вместе с частицей, так что относительно нее частица покоится) обладает определенной энергией покоя 0
, однозначно связанной с массой этой частицы.