d – срок хранения вклада в днях;
К – продолжительность года в днях;
p – процентная ставка банка, %;
Sn – величина депозита в конце срока, д.е.
Если банк начисляет простые проценты, то Sn вычисляется по формуле
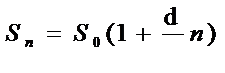
Если в середине срока вкладчик снял половину от положенной в банк суммы:

Или после приведения:
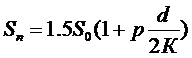
Технология решения задачи следующая.
Таблица 1
Размещение данных на рабочем листе Excel
|
A |
B |
|
|
1 |
Начальная сумма (S0) |
|
|
2 |
Срок хранения (d) |
=6*365+4*30+15 |
|
3 |
Процентная ставка (p) |
5% |
|
4 |
Величина депозита в конце срока (Sn ) |
=1,5*B1*(1+B3*B2/(2*365)) |
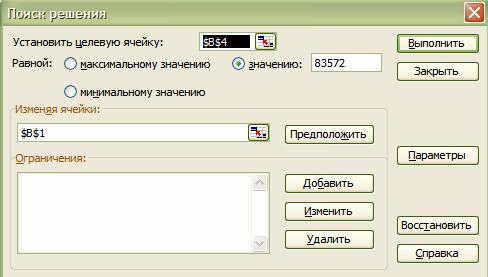
Рис. 1. Окно диалога «Поиск решения»
Таблица 1
Полученные результаты
|
A |
B |
|
|
1 |
Начальная сумма (S0) |
48061,10 |
|
2 |
Срок хранения (d) |
2325 |
|
3 |
Процентная ставка (p) |
5% |
|
4 |
Величина депозита в конце срока (Sn ) |
83572 |
Таблица 3
Описание технологии решения задачи
|
№ пп |
Что сделать |
Как сделать |
|
1 |
Разместить данные на рабочем листе Excel |
• в ячейки А1, А2, А3, А4 записать соответственно: начальная сумма (S0), срок хранения (n), процентная ставка (p), величина депозита в конце срока (Sn ) • в ячейку B2 записать формулу: =6*365+4*30+15 • в ячейкe B3 записать данные задачи: 5% • в ячейку B4 записать формулу: =1,5*B1*(1+B3*B2/(2*365)) |
|
2 |
Сделать копию экрана |
нажать клавишe Print Screen |
|
3 |
Вызвать графический редактор |
Программы – Стандартные - Paint |
|
4 |
Вставить рисунок |
Правка - Вставить |
|
5 |
Выделить нужную часть рисунка |
Выделение – выделить нужную область левой кнопкой мыши |
|
6 |
Копировать выделение |
Правка – Копировать |
|
7 |
Вызвать текстовый редактор Word |
Программы - Word |
|
8 |
Вставить из буфера обмена в документ Word |
Правка - Вставить |
|
9 |
Распечатать полученный текстовый документ |
Файл - печать |
Задание №9
Математические пакеты
К настоящему моменту разработано уже огромное количество методов для численного решения задач, встречающихся в реал
ьной жизни, прежде всего — задач, сводящихся к математическим: решению уравнений и систем уравнений, линейных и нелинейных, обыкновенных, дифференциальных или интегро-дифференциальных... Этим методам посвящены тома специальной литературы, и если возникает необходимость, можно написать программу для поиска решения или постановки численного эксперимента.
Но если необходимо получить приблизительный ответ в течение пары минут, да еще человеку, не знакомому с языками программирования и численными методами, то следует обратиться к программам, превращающим компьютер в специалиста по прикладной математике. Спектр таких программ довольно широк — от простых типа Eureka, Derive или TkSolver Plus до мощных систем Maple от Waterloo Maple Inc., Mathcad от MathSoft Inc., Mathematica от Wolfram Research Inc. или Macsyma от Macsyma Inc., работающих с выражениями в аналитическом виде.
Краткая характеристика
Едва ли не самой популярной математической программой является MathCAD (Mathsoft). Программа работает под управлением MS Windows и обладает наглядным интерфейсом WYWIWYG (What You See Is What You Get), обширным меню и множеством возможностей.
Программа работает с функциями в символьном представлении, позволяя их аналитически интегрировать и дифференцировать, строить графики функций в произвольном масштабе, решать уравнения и просто вычислять значения выражений. Пакет «знаком» с преобразованиями Фурье и Лапласа, Z-преобразованием, работает с комплексными величинами.
В рабочем поле программы можно подготавливать даже математические статьи, включая в них выражения, введенные или преобразованные с помощью MathCAD, и пользуясь всеми привычными возможностями редактирования и оформления документов в среде Windows.
Пакет совместим со многими популярными приложениями. Так, с помощью нового инструмента Stencil for Visio теперь можно включать вычисления и стандартную математическую нотацию Mathcad в рисунки Microsoft Visio (программа деловой графики). Модуль ODBC (Open Database Connectivity) позволяет пользователям Mathcad запрашивать информацию из SQL-совместимых баз данных, включая Microsoft Access, FoxPro и др. Улучшен обмен данными с AutoCAD.
Математический пакет Maple канадской компании Waterloo Maple Inc. (Ватерлоо, провинция Онтарио), в первую очередь, ориентирован на символьные вычисления, как-то: упрощение выражений, разложение на множители, аналитические интегрирование и дифференцирование, построение тригонометрических тождеств и т.д. Ну а кроме этого, пакет позволяет строить графики функций, решать уравнения и системы уравнений. В программу включен язык программирования с довольно широкими возможностями работы не только с математическими выражениями, но и с массивами, списками, последовательностями.
Работа с Maple может происходить в двух режимах. Во-первых, пользователь может вводить команды непосредственно в рабочем поле, называемом WorkSheet, и тут же наблюдать результат работы, во-вторых, возможно подготовить в текстовом процессоре командный файл, а потом его «прогнать» в Maple; здесь опять допускаются две возможности: запустить обработку можно как в автоматическом режиме, так и вручную, исполняя команды в произвольном порядке.
Графики, построенные программой, выводятся в отдельное окно, которое само по себе довольно интеллектуально и позволяет менять способ прорисовки, расположение осей и т.д.
В последние версии программы в качестве дополнения включена программа Maple Explorer, при наличии которой
пользователь может просматривать файлы Maple при помощи Internet Explorer или Netscape. Щелчок мыши на формуле в браузере приводит к запуску Maple на компьютере пользователя, и последний при желании может повторить расчет с различными параметрами.
Пакет Maple теперь может использовать Сеть для соединения страниц Maple с другими подобными страницами, используя URL-адреса ресурсов. Он также способен экспортировать данные в формат TeX или HTML.
В системе Mathematica есть все возможности для создания законченных программ, предназначенных для различных приложений.
Пакет Combinatorica поставляется вместе с системой Mathematica и предназначен для решения задач дискретной математики.
Пакет WorldPlot -- еще одно стандартное расширение системы Mathematica.
Optica -- это большой пакет системы Mathematica для разработки оптических систем.
С помощью системы Mathematica можно создавать обучающие программы.
Все пакеты, создаваемые в системе Mathematica, являются платформонезависимыми.
Сравнение различных пакетов
Математические пакеты, в особенности Mathcad — самый популярный пакет из вышеперечисленного списка, — позволяют специалистам в конкретной научно-технической области очень быстро освоить работу на компьютере и реализовать на них математические модели, не вдаваясь в тонкости программирования на традиционных языках (fortran, С, Pascal, BASIC и др.).
Вот конкретные преимущества работы в среде математической программы Mathcad:
· математические выражения в среде Mathcad записываются в их общепринятой нотации: числитель находится сверху, а знаменатель — внизу; в интеграле пределы интегрирования также расположены на своих привычных местах. Пользователь, читая распечатку принтера или глядя на дисплей, видит, что данная величина записана в числителе и ее рост приводит к возрастанию всего выражения. А это очень важно при анализе математических моделей, форма и содержание которых едины;
· в среде Mathcad процесс создания «программы» идет параллельно с ее отладкой. Пользователь, введя в Mathcad-документ новое выражение, может не только сразу подсчитать, чему оно равно при определенных значениях переменных, но и построить график или поверхность, беглый взгляд на которые может безошибочно показать, где кроется ошибка, если она была допущена при вводе формул или при создании самой математической модели. «Отладочные» фрагменты можно оставить в готовом документе для того, чтобы, например, еще раз убедить воображаемого или реального оппонента в правильности модели;
· в пакет Mathcad интегрирован довольно мощный математический аппарат, позволяющий решать возникающие проблемы без вызова внешних процедур. Вот неполный перечень вычислительных инструментов, доступных в среде Mathcad:
· решение алгебраических уравнений и систем (линейных и нелинейных);
· решение обыкновенных дифференциальных уравнений и систем (задача Коши и краевая задача);
· решение дифференциальных уравнений в частных производных;
· статистическая обработка данных (интерполяция, экстраполяция, аппроксимация и многое другое);
· работа с векторами и матрицами (линейная алгебра и др.);
· поиск минимумов и максимумов функциональных зависимостей;
· пакет Mathcad дополнен справочником по основным математическим и физико-химическим формулам и константам, которые можно автоматически переносить в документ без опасения внести в них искажения, увы, нередкие при ручной работе;
· к пакету Mathcad можно приобрести те или иные электронные учебники по различным дисциплинам: решение обыкновенных дифференциальных уравнений, статистика, термодинамика, теория управления, сопротивление материалов и т.д. Прежде чем решать возникшую проблему, пользователь может изучить электронный учебник и перенести из него в свой документ нужные фрагменты, отдельные формулы и константы;
· решая поставленную задачу, пользователь может вводить не только числовые значения переменных, но и дополнить их размерностями. При этом пользователь вправе выбирать и систему единиц (СИ, кг-м-с, г-см-с, британская), и конкретные размерности (мм, дюймы, футы и т.д.): система Mathcad в них сама разберется и выдаст ответ с заданной пользователем размерностью;
· система Mathcad оборудована средствами анимации, что позволяет реализовать созданные модели не только в статике (числа, таблицы, графики), но и в динамике (анимационные клипы);
· в систему Mathcad интегрированы средства символьной математики, что позволяет решать поставленные задачи (этап задачи) не только численно, но и аналитически;
· не выходя из среды Mathcad, возможно открывать новые документы на других серверах и пользоваться теми преимуществами информационных технологий, предоставляемых Internet;
Кроме того, не следует забывать, что пакет Mathcad — это полноценное Windows-приложение. Решая поставленную задачу, можно в статике (через буфер обмена Windows) или в динамике (OLE-технологии) передать данные в среду другой программы (в среду языка fortran, например) и там решить часть задачи.
Maple, пожалуй, самая удачно сбалансированная система, бесспорный лидер по возможностям символьных вычислений. Оригинальный символьный "движок" сочетается с легкозапоминающимся структурным языком программирования. Maple легко может быть использован и для небольших задач и для серьезных проектов. Большой "плюс" Maple - высокая интеграция среды, отличный Help.
Mathematica - одна из самых мощных систем. Обладает исключительно большой функциональной избыточностью (есть даже возможность синтезирования звука). Большой выигрыш Mathematic'е дает высокая скорость численных вычислений. К недостаткам следует отнести необычный язык программирования, который компенсируется достаточно подробной системой помощи.
Виды математических пакетов![]()
|
Математические пакеты |
|
Maple |
|
Mathcad |
|
Mathematica |
|
И другие |
|
Функции математических пакетов
|
|
решение алгебраических уравнений и систем |
|
решение дифференциальных уравнений и систем |
|
статистическая обработка данных |
|
работа с векторами и матрицами |
|
поиск минимумов и максимумов |
|
Графические построения |
|
Достоинства |
|
WYSIWYG-peдактор |
|
Интерфейс Windows |
|
OLE-технологии |
|
Высокая скорость ваычислений |





Рис. 2. Логико-смысловая модель
Список использованной литературы
1. Excel 2000: Справочник. – СПб.: Питер, 2001. – 512 с.
2. Богумирский Б.С. Руководство пользователя ПЭВМ. В 2-х ч. – СПб.: Питер, 1997.
3. Информатика: Практикум по технологии работы на компьютере: Учебное пособие для вузов / Под ред. Н. В. Макаровой. – М.: Финансы и статистика, 2003. – 2-е изд. – 256 с.
4. Информатика: Учебник для вузов / Под ред. Н. В. Макаровой. – М.: Финансы и статистика, 2001. – 3-е изд. – 768 с.
5. 15 Информационные технологии (для экономистов): Учеб. пособие / Под общ. ред. А. К. Волкова. – М.: ИНФРА-М, 2001. – 310 с.
6. Каймин В. А. Информатика: Учебник для вузов. – М.: ИНФРА-М, 2002. – 2-е изд. – 272 с.
