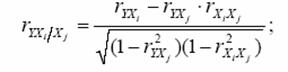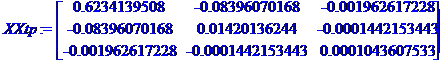
:

Уравнение имеет решение:

Получаем следующий вектор-столбец:

Свободный член 1,843401

X ₁                    0,955258

X ₂                          0,082449

У=0,955258х₁-0,082449*х₂+1,843401

2.  Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.

Влияние факторов Х на показатель Y оценивается с помощью коэффициентов эластичности Эj

Коэффициенты эластичности Эj показывают, на сколько процентов изменится значение переменной Y при изменении Хj на 1%.

Средние значения:

X₁=6,19

X₂=22,36

У=9,6

Тогда коэффициенты эластичности будут равны:

У=0,955258х₁-0,082449*х₂+1,843401

Вычисление коэффициентов эластичности показало, что переменная У изменяется гораздо быстрее при изменении переменных Х, особенно большое влияние оказывает переменная х₁.

Обычно, степень зависимости двух или более предикторов (независимых переменных X) с зависимой переменной (Y) выражается с также помощью коэффициента множественной корреляции R. По определению он равен корню квадратному из коэффициента детерминации. Это неотрицательная величина, принимающая значения между 0 и 1.

В нашем случае R =0,946558591, что говорит о большой связи между факторами.

Для интерпретации направления связи между переменными смотрят на знаки (плюс или минус) регрессионных коэффициентов. Если коэффициент положителен, то связь этой переменной с зависимой переменной положительна; если коэффициент отрицателен, то и связь носит отрицательный характер. Конечно, если коэффициент равен 0, связь между переменными отсутствует.Таким образом, можно интерпретировать так, что факторы X при их росте играют на повышение результативного параметра у. то есть при росте удельного веса рабочих высокой квалификации в общей численности рабочих (в меньшей степени) и увеличении ввода в действие новых основных фондов (в большей степени) растет выработка продукции на одного работника.

3.  Оцените статистическую значимость уравнения в целом с помощью F- критерия.

Средствами регрессионного анализа вычисляется F-критерий значимости регрессии для уравнения в целом. Это рассчитанное по наблюденным данным значение F_p (F расчетный, наблюденный) следует сравнивать с соответствующим критическим значением F_k, (F критический, табличный). Fк

выбирают из публикуемых статистических таблиц на заданном уровне вероятности (на том, на каком вычислялись параметры модели - 95%).

Вычисления показывают F_p = 0,9729 (функция ЛИНЕЙН  Excel). Если наблюденное значение Fp окажется меньше критического значения Fk, то уравнение нельзя считать значимым. В иной терминологии об этом же может быть сказано: не отвергнута нуль-гипотеза относительно значимости всех коэффициентов регрессии в постулируемой модели, т. е. коэффициенты практически равны нулю.

4.  Оцените статистическую значимость параметров регрессионной модели с помощью F- крите­рия.

F – критерий Фишера:

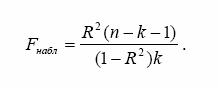
Коэффициент детерминации (R2):

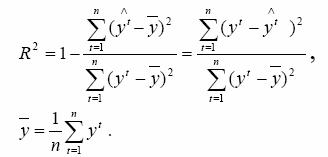
Получаем при R²=0,0352

  Если F_набл> F_таб,  то уравнение регрессии значимо.

 Если F_набл > F_кр = F_табл(0,95; n – 1; n – k – 1), где 0,95 – уровень доверительной вероятности, (n – 1) и (n – k – 1) степени свободы модели, то модель считается значимой, и принимается гипотеза о линейной регрессии между переменными Y и Xi, где Fтабл – табличное значение F-критерия Фишера.

F_табл(0,95; 19; 16)= 3,734

Следовательно полученную модель нельзя считать значимой

5.  Рассчитайте матрицы парных и частных коэффициентов корреляции, на их основе и по f-критерию для коэффициентов регрессии отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.

Таблица 2

Матрица парных коэффициентов корреляции

	Х1	Х2	У
Х1	1
Х2	0,942512	1
У	0,969881	0,939768	1

Если парный коэффициент корреляции меньше 0,1, то связи нет  если меньше 0,3, то связь слабая, если  меньше 0,5, то связь  умеренная, если  меньше  0,7, то связь заметная.  Если парный коэффициент корреляции меньше  0,9, то связь сильная, если  меньше  или равен 0,99, то связь весьма сильная, а при значении равном единице связь полная. Естественно в данном случае имеются ввиду соответствующие интервалы от предыдущего значения до следующего. Используя указанные правила построим  таблицу 3.

Таблица 3

Матрица связи между факторами

	Х1	Х2	У
Х1	1
Х2	Весьма сильная	1
У	Весьма сильная	Весьма сильная	1

Частные коэффициенты корреляции:

r_yx1/x2=(0.969881-0.939768*0.942512)/(√((1-0.939768²)(1-0.942512²)))= 0.73660585

r_yx2/x1=(0.939768-0.969881*0.942512)/(√((1-0,969881²)(1-0.942512²)))= 0.3150408

Как видим, частные коэффициенты корреляции существенно отличаются от парных коэффициентов корреляции. Частные коэффициенты корреляции используют при выборе наилучшего уравнения регрессии методом исключения переменных. Вначале рассчитывается уравнение с полным набором переменных и далее из него последовательно исключаются факторы с минимальными значениями коэффициентов частной корреляции.

Как видно из результатов расчетов, можно выделить переменную х₁ для исключения из уравнения регрессии так как налицо более слабая связь, что видно из анализа частных коэффициенты корреляции.

Получаем:

Y=0,337х₂+2,055

При этом:

 F_табл(0,95; 19; 16)= 2,31

F -критерий для оценки значимости включения переменной  x в модель:

Следовательно полученную модель можно считать значимой.

6.  Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80 % от их максимальных значений.

Таблица 4

	Х1	Х2	У прогноз
Максимальное значение факторов	9,6	36
80 % от их максимальных значений	7,68	28,8	6,805

7.  Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости а = 0,05.

Из таблиц t-распределения для числа степеней свободы ν=n-1=19 и α=0,05 найдем tα =2,0930.

Тогда точность оценки равна

Где S=10.71 -среднее квадратическое отклонение

Δ=2,0930*10.71/√(20-1)= 5.14

Доверительный интервал совокупности У равен 9.6±5.14 т.е (4.46; 14.74)

Таким образом, значение прогноза укладывается в доверительный интервал.

Список использованной литературы

1. Говорухин В., Цибулин В.,  Компьютер в математическом исследовании. Учебный курс, -СПб.: Издательство "Питер". 2003.

2. Исследование операций в экономике / Под ред. Н.Ш. Кремера. – М.: ЮНИТИ. 1997.

3. Количественный анализ хозяйственных операций и управленческих решений. –М.: "ДИС". 2004.

4. Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем, -М.:  "ДИС". 2004

5. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. – М.: Финансы и статистика, 1998.

6. Экономико-математические модели и методы / Под общей ред. А.В. Кузнецова. –Мн.: БГЭУ, 2000.