Задание 2
Выполнить арифметическую операцию (333 + 696=1029) в двоичной системе счисления.
101001101+1010111000=10000000101
1010111000
0101001101
10000000101
Выполнить проверку путем обратного перевода результата.
Переведем число 10000000101 из двоичной в десятеричную систему счисления:
100000001012=1*210 +1*22+1*20=1024+4+1=102910
Задание 3
Выполнить арифметическую операцию (696 – 333=363) в двоичной системе счисления.
10000000101-1010111000=101101011
1010111000
0101001101
101101011
Выполнить проверку путем обратного перевода результата.
Переведем число 101101011 из двоичной в десятеричную систему счисления:
1011010112=1*28 +1*26+1*25 +1*23 +1*21+1*20=256+64+32+8+2+1=36310
Задание 4
Выполнить арифметическую операцию (696 * 333=231768) в двоичной системе счисления.
10000000101-1010111000=111000100101011000
1010111000
0101001101
1010111000
1010111000
1010111000
1010111000
1010111000______
111000100101011000
Выполнить обратный перевод результата.
Переведем число 111000100101011000 из двоичной в десятеричную систему счисления:
1110001001010110002=1*217 +1*216+1*215 +1*211+1*28+1*26 +1*24+1*23=131072+65536+32768+2048+256+64+16+8=23176810
Задание 5
Составьте схему и таблицу истинности для выражения А * В + С =>Р;
Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
|
Переменные |
Промежуточные логические формулы |
Формула |
|||
|
А |
В |
С |
А * В |
С |
Р |
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю А поставим в соответствие логическую переменную а, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то а равно нулю.
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости. Схема, адекватная данному в условии логическому выражению приведена на рис. 1.
SHAPE
\* MERGEFORMAT А В С Р
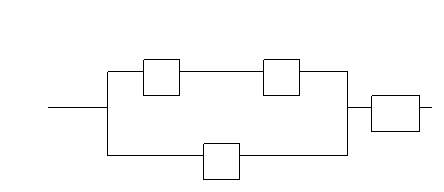

Рис. 1. Схема выражения А * В + С =>Р
