Обозначим месячный доход потребителя через М=24 кроны. общем виде задача состоит в том, чтобы максимизировать функцию полезности:
U=U(Q1, Q2,...,Qn) ®max;
при бюджетном ограничении: M=P1Q1+P2Q2 +...+PnQn, где M величина бюджета.
Бюджетное ограничение потребителя можно записать в форме следующего равенства:
М = P1 X1 + P2 X2
U=3* X1*Х2→max
которой в данном случае можно дать следующую интерпретацию: потребитель стремится получить максимум полезности от приобретенных благ (первое слагаемое функции Лагранжа) и небольшой суммы денег (второе слагаемое), оставшейся у него вследствие ограниченной делимости благ.
Тогда сомножитель Лагранжа характеризует предельную полезность денег (бюджета).
Из условий достижения максимума функции:
,
следует, что потребитель при заданных ценах и бюджете максимизирует свою функцию полезности, если отношение предельной полезности блага к его цене одинаково по всем благам и равно предельной полезности денег:
,
где 
-
предельная полезность i-го блага.
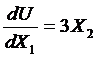
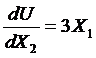
Следовательно
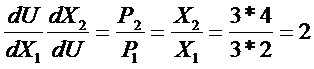
Решая совместно с уравнением бюджетного ограничения получим:
Р2 = 12/5, Р1 = 24/5
Из определения нормы замещения.
С другой стороны, по определению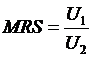 
, где U - полезность, следовательно, 
.
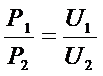То есть MRC=3X2/3X1=1/8
Задача 2
Определите коэффициент перекрестной эластичности товаров X и Y, если функция спроса на товар X задается как Qx = 4 - Рх + 0,5 * Ру; цена товара X - 10 фунтов, а товара Y - 6 фунтов. Являются ли эти товары комплементами или субститутами?
Количественной характеристикой взаимозависимости объема
предложения одного блага от цены другого служит коэффициент перекрестной
эластичности спроса (
),
который показывает, на сколько процентов изменится объем спроса блага i
при изменении цены блага j на один процент:
.
Qx=4-10+0.5*6=-3
ΔPy=0.01*6==0.06
ΔQx=-3-(4-10+0.5*6.06)=-3-(-2.97)=0.03
exy=(0.03/0.06)*6/(-3)=-1
Если eij > 0, то товары i и j называют взаимозаменяемыми , повышение цены j -того товара ведет к увеличению спроса на i-тый (например, различные виды топлива).
Если eij < 0, то товары i и j называют взаимодополняющими, повышение цены j -того товара ведет к падению спроса на i -тый (например, автомашины и бензин).
Если eij = 0, то такие товары называют независимыми , повышение цены одного товара не влияет на объем спроса на другой (например, хлеб и цемент).
Таким образом, по результатам вычисления товары Х и У являются комплиментами, то есть взаимодополняющими.
Задача 3
Спрос на продукцию отрасли задается уравнением Qd = 55 - Р, а совокупное предложение отрасли Qs = 2*Р - 5. Функция издержек конкурентной фирмы, работающей на этом рынке, задана уравнением ТС = 1,5* q2 + 5*q - 9,5. где через q обозначается объем производства данной фирмы. Определить равновесную цену и тот объем производства фирмы, который максимизирует ее прибыль.
Qd= Qs, 55 - Р = 2Р - 5
Под общей выручкой фирмы (TR) понимается полная сумма выручки от реализации всех Q, произведенных единиц товара:
TR = Р q,
где P - цена реализации.
Средняя выручка (AR) - это средняя выручка от реализации одной единицы товара:
AR = TR/ q = P q / q = Р
Средняя выручка равна цене единицы товара.
Найдем значение выпуска продукции q, максимизирующее чистую прибыль Р. В соответствии с определением
П = TR – ТС= 25q-1,5q2 + 9,5
Необходимое условие максимума функции есть равенство ее первой производной нулю.
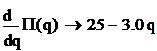
Таким образом, максимальный прибыль фирма получит при объеме производства q=25/3=8,3 ед. товара.
Задача 4
Спрос на товар монополиста задан уравнением Р = 144 - 3*Q, а средние издержки монополии могут быть представлены как АС = 25 / Q + Q. Определить рыночную цену товара и объем выпуска монополии, максимизирующей свою прибыль.
Общие издержки фирмы TC=АС*Q=25+Q2
TC’=2Q
Прибыль монополии достигает максимума при 144-3Q=2Q
Откуда Q=28.8; P=57.6
Список литературы
1. Гальперин В.М., Игнатьев С.М., Моргунов В.И. "Микроэкономика". М: изд. "Экономическая школа". 2002.
2. Введение в микроэкономику. М: изд. "Экономическая школа". 2001
3. Общая экономическая теория (политэкономия): учебник, Под общ. ред. В.И.Видяпина, Г.П.Журавлевой, -М.: ПРОМО-Медиа, 2003.
4. Тарасевич Л.С., Микроэкономика, -М., Юрайт, 2003.