2.  Сведите    задачу     к    двумерному    виду.     Представьте графически    множество   допустимых   решений.    Решите задачу поиска оптимального плана методом перебора и графическим методом, с учетом целочисленного характера  переменных.

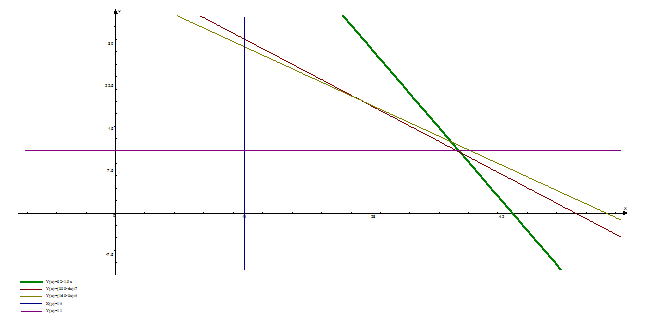
Необходимо построить прямые ограничивающие область допустимых решений. Каждая прямая соответствует одному неравенству системы неравенств ограничений. Для получения координат двух точек по которым строится прямая знаки неравенств заменяют на равенства и находят корень полученного уравнения относительно каждой переменной. Таким образом получаются точки пересечения прямой с осями координат. Построив прямую определяют область допустимых решений ограничивающуюся этой прямой путем исследования точек находящихся по обе стороны прямой на удовлетворение их координат соответствующему этой прямой неравенству. Так получается область допустимых решений ограниченная прямыми.

Однако нам необходимо найти такую точку, в которой достигался бы максимум целевой функции. Для этого построим произвольную прямую 1,5х₁+1,35х₂= 0, как x ₁  = -1,35х₂/1,5+40 (число 40 произвольное). Обозначим эту линию РР. В каждой точке этой линии прибыль одинакова. Перемещая эту линию параллельно ее исходному положению, найдем точку, которая удалена от начала координат в наибольшей мере, однако не выходит за пределы области допустимых решений. Это точка М, которая лежит на вершине многоугольника. Координаты этой точки (x₁  = 11 и x₂  = 37) и будут искомым оптимальным планом.

3.  Дайте      экономическую      интерпретацию      оптимального                        решения.

Таким образом, необходимо выпустить x₁  = 11 шт. изделий 1, x₂  = 37 изделий 2, чтобы получить max прибыли.                                                                                                         

Решение задачи методом перебора сводится к последовательному нахождению вершин и выбору максимального значения из полученных.

Пересечение функций d₃=11 и d₄=14 является точка (14 ,11).

Ц(f)=31,4

Пересечение функций d₃=11 и 7х₁+6х₂=300 является точка (37,6, 11).

Ц(f)=66,7

Пересечение функций d₄=14 и 4х₁+3х₂=160 является точка (16, 28).

Ц(f)=63,6

Пересечение функций 8,5х₁+6х₂=340 и 6х₁+4,5х₂=250 является точка (20, 26,67).

Ц(f)=62,1

Таким образом, Ц(f)=66,7 будет максимальным значением.

4.  Оцените    (качественно)    чувствительность   оптимального                        плана производства к изменению исходных условий задачи.

Целевая функция L(x) -это доход от реализации плана производства x; aij -интенсивность расходования i-го ресурса при j-м способе производства; bi- имеющийся уровень i-го ресурса.  Предположим, что величины ресурсов варьируются. Тогда возникают вопросы: при каких вариациях правых частей ограничений найденный оптимальный план x₀ не изменяется; как эти вариации влияют на функцию максимального дохода L_max? Ответ на эти вопросы дает анализ соответствующей задачи ЛП на

чувствительность.

Таким образом, оптимальные значения двойственных переменных определяют вклад каждого ресурса в доход L_max при оптимальном решении x₀. Эта величина численно равна дополнительному доходу при увеличении i-го ресурса b_i на единицу при условии, что ресурсы используются оптимальным образом.

Однако, так как в условии задачи недостаточно данных для оценки ресурсов, то по графику функции можно сделать приблизительную оценку изменения целевой функции.

Из графика видно, что целевая функция граничит с областью допустимых значений в точке пересечения минимума первых изделий и стоимости оптимального плана. Тогда ясно, что целевая функция не будет чувствительна к минимуму вторых изделий в большей степени и трудоемкости производства в меньшей степени.                     

Задача 2

5.  Сформулируйте   задачу   2   (оптимизация   перевозок)   в терминах стандартных задач линейного программирования (транспортная задача).

Потребности строек, машин			Возможности поставок, машин
w1	w2	w3	f1	f2
8	10	8	13	13

Издержки перевозок, тыс. руб
с11	с12	с13	с21	с22	с23
2	4	3	3	2	4

Проверим равенство суммарного производства машин и суммарного спроса

откуда следует вывод– задача сбалансирована, поскольку спрос на автомобили равен объему их производства.

Таблица 1

Стоимость перевозки машин, т. руб./шт.

	1	2
W1	2	3
W2	4	2
W3	3	4

Согласно результатам проверки сбалансированности задачи в транспортной матрице должно быть три строки, соответствующих заводам и два столбца, соответствующих центрам распределения (см. табл. 2). Тариф перевозки обычно вписывают в правом нижнем углу клетки матрицы для удобства дальнейшего нахождения опорных планов задачи.

Таблица 2

Транспортная матрица задачи 2

	W1		W2		W3		Возможности поставок, машин
1							13
		2		4		3
2							13
		3		2		4
Потребности строек, машин	8		10		8		26

Суммарные затраты в рублях на перевозку машин определяются по формуле

Задание ограничений

6. Постройте граф с вершинами-поставщиками, вершинами-                        потребителями и дугами с интенсивностями перевозок.

     

7. Представьте графически множество допустимых решений.                         Решите задачу поиска оптимального плана графическим  методом, с учетом целочисленного характера переменных.

1

2

поставщики

покупатели

1

2

3

2

4

3

3

2

4

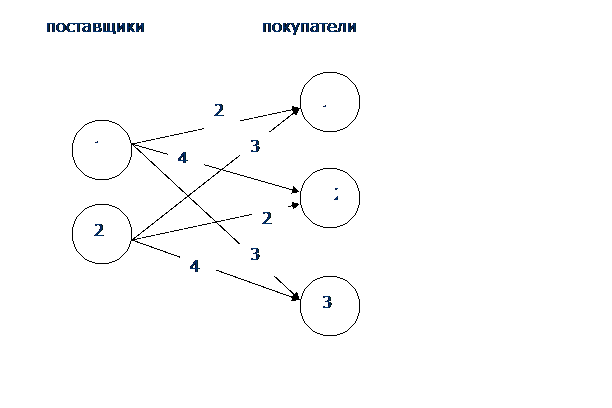
Из рисунка видно, что у первого поставщика наименьшие издержки с₁₁=2. Возможности поставок 13, машин а потребность стройки 8, следовательно маршрутом 11 уйдет 8 машин. Оставшиеся 5 машин отправляем в пункт 3.

У второго поставщика наименьшие издержки по маршруту 22. следовательно все потребные 10 машин стройки 2 уйдут по этому маршруту, остальные 3 машины пойдут по маршруту 23.

Следовательно х₁₁=8, х₃₁=5, х₂₂=10, х₂₃=3.

Проверим методом наименьшего элемента.

Находим в таблице наименьшую стоимость перевозки - это 2. Записываем в этой клетке значение 8 (наименьшее из сумм по строке и столбцу). Теперь вычеркиваем первый столбец, уменьшив сумму в первой строке на 8. Находим следующую наименьшую по стоимости ячейку -,13. Присваиваем ей значение 5, а сумму по столбцу заменяем на 3. Вычеркиваем первую строку. Выбираем ячейку 22, присваиваем ей значение 10. сумма по второй строке равна 3 - вычеркиваем второй столбец. Выбираем ячейку 33, присваиваем ей 3. Уменьшаем второй столбец на 3 и вычеркиваем вторую строку.

Таблица 3

	В1		В2		В3
А1		2		4		3	13
	8				5		5
А2		3		2		4	13
			10		3		3
	8		10		8 3

Опорный план построен.

Х₁₁=8, Х₁₃=5, Х₂₂=10, Х₂₄=3.

Все остальные Х_ij=0.

F=8*2+5*3+10*2+3*4=63

Построенный план является допустимым, так как все заявки удовлетворены, все запасы израсходованы.

Проверим, является ли полученный план опорным: количество ячеек с ненулевыми перевозками равно m+n-1=2+3-1=4

Список использованной литературы

1. Аллен Р. Математическая экономика- – М. Экономика, 2003

2. Ашманов С.А. Введение в математическую экономику. – М.: Наука, 1994

3. Вагнер Г. Основы исследования операций. Тома I-III. –М.: Экономика, 2003.

4. Интриллигатор М. Математические методы оптимизации и экономическая теория. – М.: Прогресс, 1992.

5. Колесников А. Н. Краткий курс математики для экономистов. – М.: ИНФРА-М, 2003

6. Математическая экономика на персональном компьютере (под. ред. Кубонивы М.) . – М.: ФиС, 2001

7. Экланд И. Элементы математической экономики. – М.: Мир, 1993