317.3. В основании прямого
параллелепипеда лежит ромб, диагонали которого равны 12 см и 16 см. Высота
параллелепипеда равна 8 см. Найдите площадь его полной поверхности.
Пусть d1, d2 — диагонали ромба (рис. 96), и так
как они взаимно перпендикулярпы, то длина а всех иx сторон ромба равна
(по теореме Пифагора)
Боковые ребра параллелепипеда перпендикулярны основаниям (параллелепипед
— прямой). Бокоовые грани параллелепипеда — равные прямоугольники. Следовательно,
Sбок = 4Sграни = 4ah
, где
h — высота параллелепипеда, поэтому
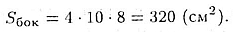
Площадь ромба Sоснвычисляется по формуле
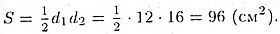
Теперь вычислим площадь полной поверхности:
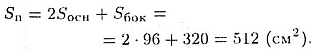
Ответ. 512 см2.
17.4. Найдите площадь боковой поверхности
правильной четырехугольной пирамиды, у которой диагональное сечение равновелико
основанию если сторона основания раина а.
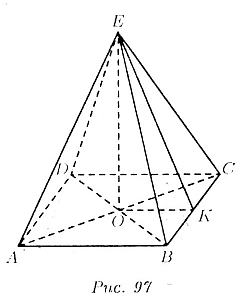
Пусть ABCDE —данная пирамида, с вершиной E и центром основания О (рис.
97).
Условие задачи означает, что
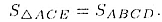
Так как АВ = а, то 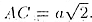 .
Равенство площадей может быть записало в виде .
Равенство площадей может быть записало в виде
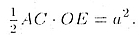
Отсюда
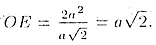
Из прямоугольного треугольника ОЕК определим апофему пирамиды ЕК:
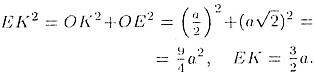
Боковая поверхность Sбок пирамиды равна:
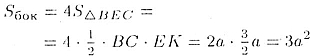
Ответ. 3a2.
|