314.3. Сферу на расстоянии
8 см от центра пересекает плоскость. Радиус сечения ранен 15 см. Найдите
площадь сферы.
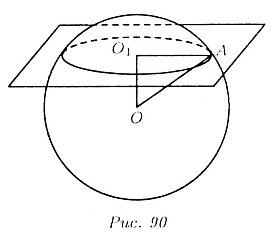
Сечение сферы с плоскостью есть окружность с центром О1 радиуса
О1А (рис. 90). Мри этом ОО1 (О - центр cферы) пернендикулярно
О1А. Радиус R сферы найдем из прямоугольного треугольника ОО1А:
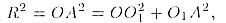
где
ОО1 = 8 см,
О1А = 15 см
Получаем
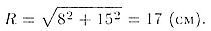
Площадь сферы S радиуса R равна 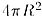 .
Следовательно, .
Следовательно,
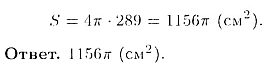
314.4. Через сторону нижнего основания правильной
треугольной призмы проведена плоскость, пересекающая боковые грани по
отрезкам, угол между которыми равен 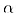 .
Найдите угол наклона этой плоскости к основанию призмы. .
Найдите угол наклона этой плоскости к основанию призмы.
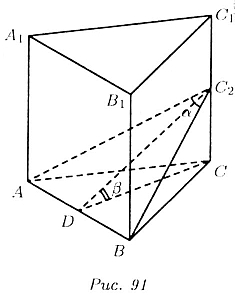
Обозначим сторону основания призмы ABCA1B1C1
буквой а (рис. 91). Пусть плоскость проведена через ребро АB и пересекает
ребро СС1 в точке СС2. Тогда, из равностороннего
треугольника ABC находим
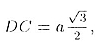
где DC — высота (медиана, биссектриса) треугольника. Так как 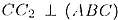 и
и 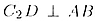 то то 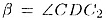 —
искомый угол между сечениями AС2В и оснонапием АСB. Из прямоугольного
треугольника —
искомый угол между сечениями AС2В и оснонапием АСB. Из прямоугольного
треугольника 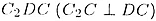 получаем соотношение
получаем соотношение
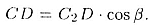
С другой стороны, из 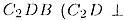 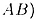 имеем равенство
имеем равенство
Из последних двух равенств следует, что
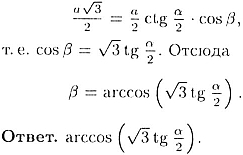
|