312.3.
Радиус основания конуса равен 14 см. Найдите площадь сечения, проведенного
перпендикулярно его оси через ее середину.
Способ 1. Радиус О1С1 сечении конуса (рис. 80)
представляет собой среднюю линию треугольника следовательно,
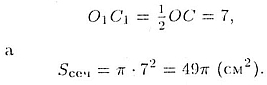
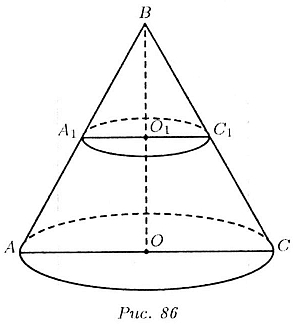
Способ 2. Площадь основания конуса равна
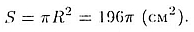
Площади сечений конуса относятся как квадраты расстояний от их центров
до вершины:
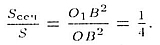
Следовательно,
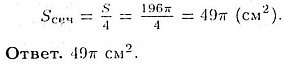
312.4. В цилиндр наклонно вписан квадрат
так, что все его вершины лежат па окружностях оснований. Найдите сторону
квадрата, если высота цилиндра раина 2 см, а радиус основания равен 7
см.
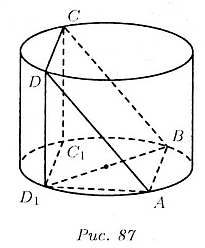
Пусть ABCD — квадрат, о котором идет речь в условиях задачи (рис. 87).
Обозначим его сторону через х:
АB = АD = х.
Проекции томек С и D па нижнюю окружность обозначим через С1
и D1. Фигура АВС1D1 — прямоугольник,
так как
С1D1 = CD = АВ
и
С1D1 || CD || АВ
Обозначим:
AD1 = у. Используем
теорему Пифагора
в прямоугольных
треугольниках:
I. Треугольник
ABD1 со сторонами
x, у и BD1 —2*7 (диагональ
BD1 прямоугольника
является диаметром
окружности):
x2 + у2 = 142 = 196.
2. Треугольник
AD1D со сторонами
AD1= y,
D1D = 2
и AD = x
т. е.
ó2 + 22 = x2
x2 - ó2 = 4
Складывая почленно
уравнения, находим
2х2 =200
т.е
x = 10.
Ответ. 10 см.
|