38.3. Высота прямой призмы
равна 10 см, а ее основанием является прямоугольник, стороны которого
равны 8 см и 6 см. Найдите плошадь диагонального сечения.
Диагональное сечение АСС1A прямой призмы ABCDA1B1C1D1
(рис. 78) представляет собой прямоугольник с основанием АС и высотой AA1,
а его площадь
S = АС • AA1
Длину АС находим ич прямоугольно го треугольника ABC по теореме Пифагора:
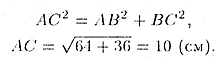
Следовательно
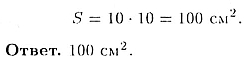
38.4. Тело ограничено двумя концентрическими
шаровыми поверхностями. Докажите, что его сечение плоскостью, проходящей
через центр, равновелико сечению, касательному к внутренней шаровой поверхности.
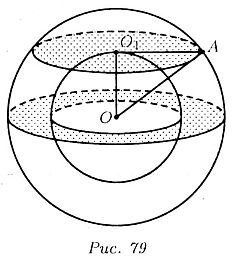
На рис. 79 оба сечения заштрихованы. Пусть R и r радиусы шаров. R >
r. Тогда сечение плоскостью, проходящей через центр, представляет кольцо,
ограниченное концентрическими окружностями радиусов R и r. Его площадь
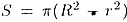 — разность
площадей большего и меньшего кругов. — разность
площадей большего и меньшего кругов.
Сечение, касательное к меньшей сфере, есть круг радиуса R1,
который определим из прямоугольного треугольника ОО1А с ОА
= R и ОО1 = r. Получаем
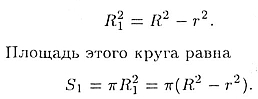
Площади сечений равны S1 = S. Требуемое доказано.
|