| 36.3. В основани пирамиды
лежит прямоугольный треугольник, гипотенуза которого равна 15 см, а один
Hi катетом — 9 см, Найдите площадь сечения, проведенною через середину
высоты пирамиды параллельно ее
основанию.
На рис. 74 изображена пирамида SABC. Основание АBС- прямоугольный треугольник
с  , АB = 15
см, AC = 9 см. Сечение пирамиды плоскостью, проходящей через середину , АB = 15
см, AC = 9 см. Сечение пирамиды плоскостью, проходящей через середину
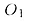 высоты SO
пирамиды паралельно основанию, представляет собой прямоугольный треугольник высоты SO
пирамиды паралельно основанию, представляет собой прямоугольный треугольник
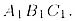
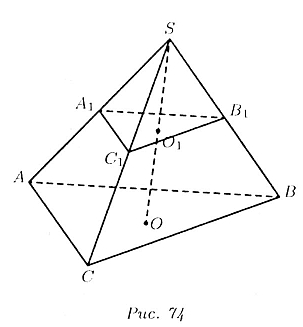
Известно, что треугольник 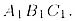 подобен треугольнику ABC и площадь треугольника
подобен треугольнику ABC и площадь треугольника 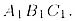 относится
к площади треугольника ABC как квадрат их расстояний от вершины пирамиды,
т.е. относится
к площади треугольника ABC как квадрат их расстояний от вершины пирамиды,
т.е.
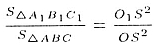
По теореме Пифагора находим
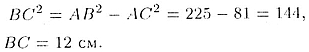
Площадь треугольника ABC равна
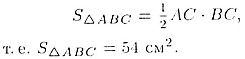
Так как 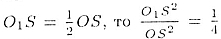 и
и
из пропорции, приведенной выше, находим
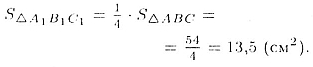
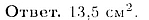
36.4. Плоскости  пересекаются
по прямой a, и перпендикулярны плоскости пересекаются
по прямой a, и перпендикулярны плоскости  Докажите,
что прямая a перпендикулярна плоскости Докажите,
что прямая a перпендикулярна плоскости 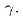
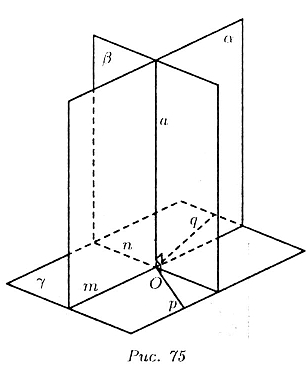
Пусть плоскости 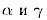 пересекаются
по прямой пересекаются
по прямой 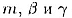 -
по прямой n -
по прямой n
А прямые a, m, n имеют общую точку О (рис. 75).
Так как дано, что 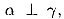 ,
то линейный угол двугранного угла между а и ,
то линейный угол двугранного угла между а и 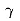 -
прямой. Следовательно, если через точку О пронести прямую р и плоскости -
прямой. Следовательно, если через точку О пронести прямую р и плоскости
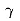 так, что так, что 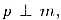 ,
то угол между а и р равен 90°. Аналогично (так как ,
то угол между а и р равен 90°. Аналогично (так как 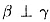 )
если через О пронести прямую q в плоскости )
если через О пронести прямую q в плоскости 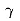 причем причем
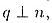 , то угол
между а и n равен 90°. Получили, что прямая а перпендикулярна двум прямым
р и q плоскости , то угол
между а и n равен 90°. Получили, что прямая а перпендикулярна двум прямым
р и q плоскости 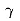 ,
кроме того, р и q проходят через точку О. Из признака перпендикулярности
прямой и плоскости следует, что ,
кроме того, р и q проходят через точку О. Из признака перпендикулярности
прямой и плоскости следует, что 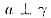 и требуемое доказано.
и требуемое доказано.
|