35.3. Найдите площадь сечения
шара радиуса 41 см, проведенною на расстоянии 9 см от центра.
На рис. 7'2 изображен шар с центром О радиуса ОA = 41 см и сечении шара
с плоскостью a, представляющее круг с центром в точке B и радиуса r =
BA.
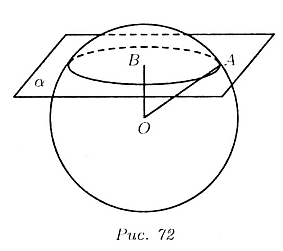
При этом ОB перпендикулярен плоскости a и ОВ = 9 см. Площадь кругового
сечения равна 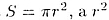 определим из прямоугольного треугольника ОВА. Имеем
определим из прямоугольного треугольника ОВА. Имеем
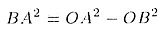
(теорема Пифагора), т.е.
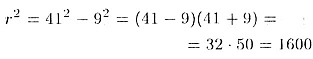
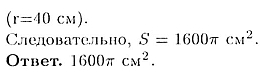
35.4. Через концы отрезка АB, пересекающего
плоскость а, и его середину М проведены параллельные прямые, пересекающие
плоскость a в точках 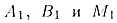 .
Найдите длину отрезка .
Найдите длину отрезка 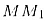 ,
если ,
если 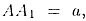 a a
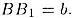
Сначала «пространственную» задачу сводим к «плоской». Для этого через
параллельные прямые 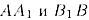 проводим плоскость
проводим плоскость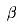 .
Она пересечет плоскость а по прямой .
Она пересечет плоскость а по прямой 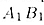 .
На рис. 73 изображена плоскость .
На рис. 73 изображена плоскость 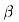 (буквой
а обозначено пересечение плоскостей a и (буквой
а обозначено пересечение плоскостей a и 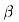 ).
Кроме этого, на рис. 73 реализована одна из трех возможностей: точка A
более удалена от плоcкости a, чем точка B. т.е. ).
Кроме этого, на рис. 73 реализована одна из трех возможностей: точка A
более удалена от плоcкости a, чем точка B. т.е. 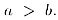 .
В этом случае через точку В проводим прямую c, параллельную .
В этом случае через точку В проводим прямую c, параллельную 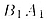 ,
и точки ее пересечения с продолжениями ,
и точки ее пересечения с продолжениями 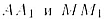 обозначим
буквами D и С соответственно. Получим треугольник ABD обозначим
буквами D и С соответственно. Получим треугольник ABD
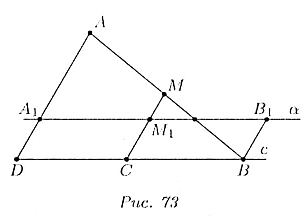
Поскольку 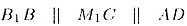 и
и 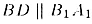
то
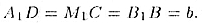
В 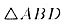 имеем
AD= а + b, a MС — средняя линия, так как M — середина AB и MC||AD. Значит, имеем
AD= а + b, a MС — средняя линия, так как M — середина AB и MC||AD. Значит,
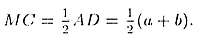
Следовательно,
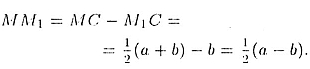
Вторая возможность: точка B более удалена от плоскости а, чем A, т.е.
b > а. В таком случае можно поменять местами буквы A и B и соответственно
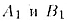 . Получили
бы . Получили
бы
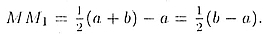
Третья возможность: a = b т. е. M — пересечение АВ с плоскостью а. Тогда
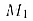 совпадает
с М и совпадает
с М и
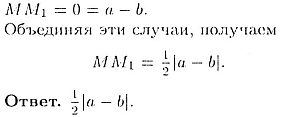
|