Geum.ru


начало раздела: Шпаргалки

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ
 
В случаях растяжения-сжатия (а) или кручения (б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях (рис.1.11а.б).
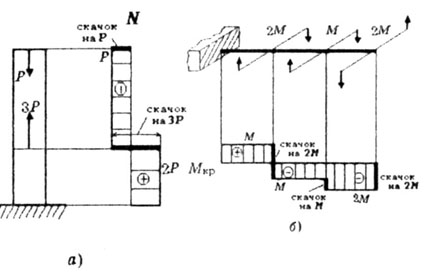Рис. 1.11
Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений.
Каждая эпюра на своих участках имеет знаки.
Правила знаков для внутренних усилий, применяемые в машиностроении.
  1. Продольная сила N считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.
  2. Поперечная сила О считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.
  3. Эпюра изгибающих моментов строится на сжатых волокнах. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна
  4. Правило знаков для крутящего момента принимается произвольным.
Обычно уславливаются, что при взгляде на нормаль к отсеченной части внутренний крутящий момент считается положительным, если он крутит отсеченную часть по часовой стрелке.
При изгибе между поперечной силой Q, изгибающим моментом М, углом поворота поперечного сечения 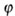и прогибом Y существуют дифференциальные зависимости, позволяющие установить следующие характерные особенности эпюр:

1. Записываем выражение изгибающих моментов для текущего сечения z, например, в консольной балке, находящейся под действием сосредоточенной силы (рис. 1.12):

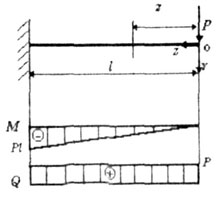Рис. 1.12
М = - P*z - уравнение прямой.
В соответствии с дифференциальной зависимостью Журавского:
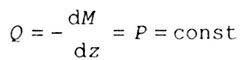Из этого следует, что на прямолинейном ненагруженном внешней пролетной нагрузкой участке стержня эпюра моментов М прямолинейна, а эпюра поперечных сил Q постоянна (рис. 1.12).

2. В точке приложения сосредоточенного изгибающего момента эпюра моментов М имеет скачок на величину этого момента, а эпюра поперечных сил О постоянна.В точке приложения сосредоточенного крутящего момента эпюра крутящих моментов Мкр имеет скачок на вепичину этого момента рис. 1.11 ,б).

3. В точке приложения сосредоточенной поперечной силы эпюра изгибающих моментов имеет излом острием навстречу силе, а эпюра поперечных сил - скачок на величину этой силы.

В точке приложения сосредоточенной продольной силы эпюра продольных сил А/ также имеет скачок на величину этой силы.

4. Записываем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием распре-лйпвнной нагрузки (оис.1.13 а):

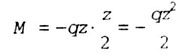уравнение квадратной параболы.
В соответствии с дифференциальной зависимостью Журавского:
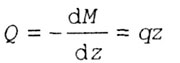уравнение прямой.
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов М очерчены по квадратной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил Q имеет вид трапеции или треугопьника. И очерчена прямой, наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением q (рис. 1.13 а, б, в).
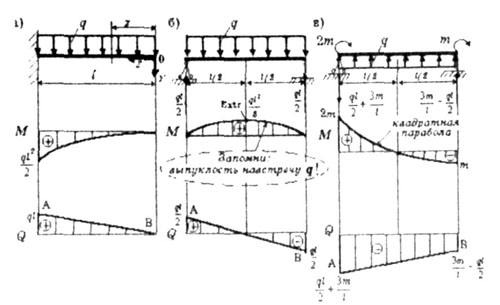Рис. 1.13