Пусть L — окружность радиуса R с центром в точке О, а
OP прямая, перпендикулярная плоскости 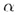 ,
содержащей окружность L. Точку Р, которую назовем вершиной конуса, соединим
со всеми точками M окружности L. ,
содержащей окружность L. Точку Р, которую назовем вершиной конуса, соединим
со всеми точками M окружности L.
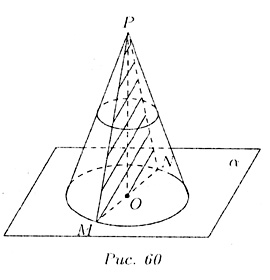
Поверхность, образованная этими отрезками, называется конической поверхностью
(рис. 60). Тело, ограниченное конической поверхностью и кругом с границей
L, называется конусом, отрезки РM -- образующими конуса, круг — основанием,
окружность — направляющей, ОР - высотой конуса, R — радиусом основания,
прямая OD -— осью конуса.
Конус может быть получен также вращением прямоугольного треугольника
ОРМ вокруг своего катета ОР. При этом боковая поверхность конуса образуется
вращением гипотенузы РМ, а круг основания — вращением катета ОМ.
Сечение конуса плоскостью, проходящей через его ось, называется осевым
сечением (на рис. 60) — это равнобедренный треугольник MPN.
Сечение конуса плоскостью перпендикуляров оси конуса является кругом,
центр которого лежит на оси конуса. Такое сечение отсекает от конуса меньший
конус, а оставшаяся часть называется усеченным конусом.
|