Пирамида называется правильной, если в ее основании лежит
правильный многоугольник, а основание ее высоты совпадает с центром этого
многоугольника. Под центром многоугольника понимается центр вписанной
или описанной окружностей. У правильной пирамиды ребра равны:
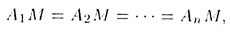
а боковые грани — равные равнобедренные треугольники (рис. 45):
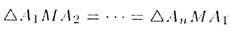
Высоты этих боковых граней также равны и называются апофемами пирамиды.
В нашем случае апофема обозначена через МК (МК _|_ A1A2,
A1K
= К А2).
Теорема. Площадь боковой поверхности пирамиды
Sбок
равна произведению n (числа сторон или вершин многоугольника основания)
на площадь одной грани.
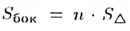
площадь одной грани (треугольника) равна

где сторона основания пирамиды равна а, а апофема равна А.
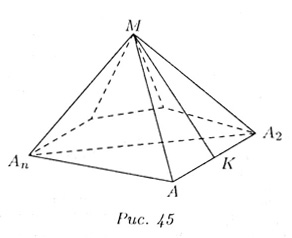
Итак,
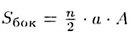
поскольку n • а представляет собой периметр основания
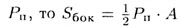
Теорема. Площадь боковой поверхности пирамиды
равна произведению полупериметра, основания на апофему.
|