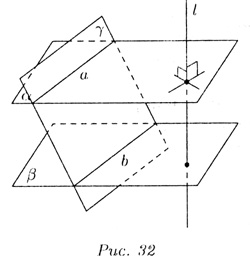
Две плоскости называются параллельными, если они не имеют
общих точек (на рис. 32, 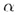 || ||
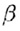 ). Две плоскости, перпендикулярные
одной прямой, параллельны. Это утверждение вытекает из единственности
плоскости, проходящей через данную точку перпендикулярно данной прямой
(рис. 32). Параллельные плоскости обладают следующими свойствами: ). Две плоскости, перпендикулярные
одной прямой, параллельны. Это утверждение вытекает из единственности
плоскости, проходящей через данную точку перпендикулярно данной прямой
(рис. 32). Параллельные плоскости обладают следующими свойствами:
1. Прямые, по которым две параллельные плоскости пересекают третью плоскость,
параллельны (рис. 32).
В самом деле. Пусть 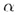 || || 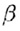 и
и 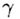 пересекает пересекает 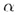 и
и 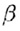 по прямым а и b. Тогда а и
b не имеют общих точек, так как они лежат в плоскостях по прямым а и b. Тогда а и
b не имеют общих точек, так как они лежат в плоскостях 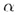 и
и 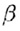 , которые не имеют общих точек.
Прямые , которые не имеют общих точек.
Прямые 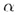 и и 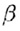 лежат в плоскости
лежат в плоскости 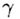 , поэтому
они параллельны. , поэтому
они параллельны.
2. Через каждую точку, не лежащую на данной плоскости, проходит плоскость,
параллельная данной, и притом только одна.
3. Две плоскости, параллельные третьей плоскости, параллельны.
|