начало раздела: Шпаргалки

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ (ТОЧНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ Ркр).

Если коэффициент приведения длины не очевиден, то Ркр можно найти, решая дифференциальное уравнение - это точный метод определения критической силы.

Особенностью задач устойчивости является тот факт, что рассматривается равновесие стержня в деформированном состоянии, в то время как в других разделах составляются уравнения равновесия для элемента нагруженного стержня (или иного тела) без участка его изменений вследствие деформаций.

Общий порядок расчета:

изобразить стержень в деформированном состоянии после потери устойчивости; отбросив опоры, заменить их реакциями (эти реакции неизвестны, изображаем их в общем виде); выбрав оси координат, по участкам применить метод сечений; в разрезе приложить все внутренние суммарные силовые факторы, направив их в положительную сторону; записать уравнение равновесия отрезанной части стержня в виде суммы моментов относительно оси X произвольного сечения; заменив изгибающий момент через кривизну и жесткость

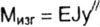получим дифференциальные уравнения равновесия в количестве, равном числу участков (при этом обозначим );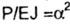

Используя граничные условия на концах стержня и условия стыковки участков (равенство перемещений и углов поворота в конце предыдущего и в начале последующего участка, так как изогнутая ось стержня - плавная кривая без изломов и разрывов), получаем так называемое характеристическое уравнение.

Решая полученное (чаще всего трансцендентное) уравнение подбором, графически или с помощью ЭВМ, получаем ряд 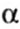значений , удовлетворяющих уравнению и граничным условиям задачи. Наименьшее (отличное от нуля) из полученных значений 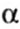дает выражение для критической силы в виде
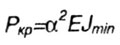