Прямая а, пересекающая плоскость 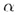 ,
называется перпендикулярной этой плоскости, если она перпендикулярна любой
прямой плоскости, проходящей через точку О пересечения прямой a и плоскости ,
называется перпендикулярной этой плоскости, если она перпендикулярна любой
прямой плоскости, проходящей через точку О пересечения прямой a и плоскости
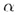 . .
Теорема. Если прямая а перпендикулярна двум
прямым b и с, плоскости 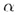 , проходящим
через точку О пересечения а и , проходящим
через точку О пересечения а и 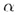 ,
то а перпендикулярна ,
то а перпендикулярна  . .
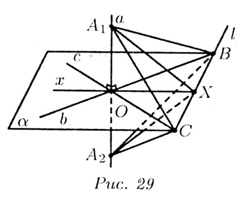
Пусть дана прямая a и две прямые b и с, лежащие в плоскости  :
а _|_ b, a _|_ с (рис. 29), О — точка пересечения b и с. Пусть х — другая
(отличная от b и с) прямая, лежащая в :
а _|_ b, a _|_ с (рис. 29), О — точка пересечения b и с. Пусть х — другая
(отличная от b и с) прямая, лежащая в  и проходящая через точку О. Надо доказать, что a _|_ x.
и проходящая через точку О. Надо доказать, что a _|_ x.
Проводом в плоскости 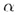 произвольную
прямую l, пересекающую прямые b и с и не проходящую через точку О. Обозначим
В = l произвольную
прямую l, пересекающую прямые b и с и не проходящую через точку О. Обозначим
В = l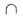 b, С = l b, С = l 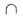 с
и X = l с
и X = l 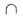 х. Берем на а две точки
А1
и А2,
так что OА1
= ОА2
(А1
и А2
— по разные стороны от х. Берем на а две точки
А1
и А2,
так что OА1
= ОА2
(А1
и А2
— по разные стороны от 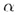 . Рассмотрим
образовавшиеся треугольники. . Рассмотрим
образовавшиеся треугольники.
1.  А1ОВ
= А1ОВ
=  А2ОВ
как прямоугольные треугольники с ранными катетами. Значит, А1В
= А2В. А2ОВ
как прямоугольные треугольники с ранными катетами. Значит, А1В
= А2В.
2.  А1ОС
= А1ОС
=  А2ОС
по аналогичной причине. Отсюда А1С
= А2С. А2ОС
по аналогичной причине. Отсюда А1С
= А2С.
3.  А1СВ
= А1СВ
=  А2СВ
по трем сторонам. Значит, < А1BC
= < А2BC
. А2СВ
по трем сторонам. Значит, < А1BC
= < А2BC
.
4. Обратимся к треугольникам А1BX
и А2BX.
В них А1B
= А2B,
ВХ — общая, < А1BX
= < А2BX
(по первому признаку). Отсюда следует, что А1X
= А2X.
Значит,  А1XА2
- равнобедренный, О — середина А1А2.
Значит, ОX - медиана, а тогда и высота, равнобедренного треугольника.
Следовательно, a _|_ х. А1XА2
- равнобедренный, О — середина А1А2.
Значит, ОX - медиана, а тогда и высота, равнобедренного треугольника.
Следовательно, a _|_ х.
|