начало раздела: Шпаргалки

ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ СИЛЫ ПО ФОРМУЛЕ ЭЙЛЕРА

Для шарнирно закрепленного, центрально-сжатого стержня постоянного сечения (рис.8.2). I Формула Эйлера имеет вид:

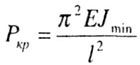где Е - модуль продольной упругости материала стержня;

Jmin - минимальный момент инерции поперечного сечения стержня.

Для стержней с другими видами закрепления формулу Эйлера записывают в виде:

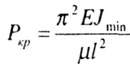где 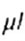- приведенная длина стержня;

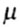- коэффициент приведения длины.

Выражение "приведенная длина" означает, что в формуле Эйлера с помощью коэффициента 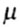все случаи закрепления концов стержня можно привести к основному, шарнирному закреплению.

Коэффициент приведения длины 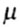иногда можно оценить по числу полуволн n, по которым выпучится стержень, теряя устойчивость, а именно, можно принять

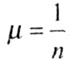На рис. 8.2 показаны наиболее часто встречающиеся на практике случаи закрепления концов стержня и соответствующие им значения коэффициента

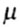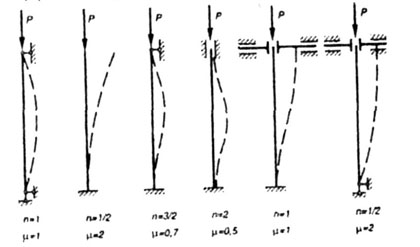Рис. 8.2

Формула Эйлера применима только о пределах выполнения закона Гука, когда критическое напряжение 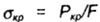не превышает предел пропорциональности материала стержня, так как эта формула была введена с помощью зависимости

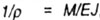в свое время полученной на основании закона Гука.

Применимость формулы Эйлера можно определить, оценив гибкость стержня и сравнив эту гибкость с ее предельным значением. Гибкость стержня равна

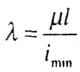где

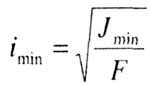- минимальный радиус инерции (геометрическая характеристика сечения);

- минимальный момент инерции площади сечения стержня.

Значение предельной гибкости 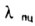получается из условия

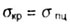Предельная гибкость равна

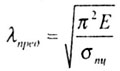Так, для малоуглеродистой стали, если принять Е = 2x105 МПа,

Для повышения несущей способности конструкций в них стремятся использовать стержни возможно меньшей гибкости. Так что расчет реальных конструкций с гибкостью 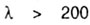практически маловероятен. Будем считать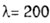

верхней границей значений гибкости реальных стержней.

Следовательно, формула Эйлера для определения критического значения сжимающей силы в виде

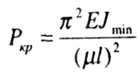применима в случае, если гибкость стержня находится в пределах

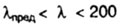(кривая СД на рис. 8.3)

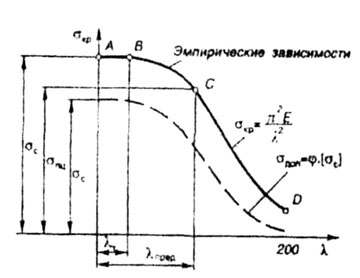Рис. 8.3

Для малоуглеродистой стали этот диапазон равен
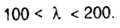